|
Liouville–Bratu–Gelfand Equation
: ''For Liouville's equation in differential geometry, see Liouville's equation.'' In mathematics, Liouville–Bratu–Gelfand equation or Liouville's equation is a non-linear Poisson equation, named after the mathematicians Joseph Liouville, G. Bratu and Israel Gelfand. The equation reads :\nabla^2 \psi + \lambda e^\psi = 0 The equation appears in thermal runaway as Frank-Kamenetskii theory, astrophysics for example, Emden–Chandrasekhar equation. This equation also describes space charge of electricity around a glowing wire and describes planetary nebula. Liouville's solution In two dimension with Cartesian Coordinates (x,y), Joseph Liouville proposed a solution in 1853 as :\lambda e^\psi (u^2 + v^2 + 1) ^2 = 2 \left left(\frac\right)^2 + \left(\frac\right)^2\right/math> where f(z)=u + i v is an arbitrary analytic function with z=x+iy. In 1915, G.W. Walker found a solution by assuming a form for f(z). If r^2=x^2+y^2, then Walker's solution is :8 e^ = \lambda \left lef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liouville's Equation
:''For Liouville's equation in dynamical systems, see Liouville's theorem (Hamiltonian).'' : ''For Liouville's equation in quantum mechanics, see Von Neumann equation.'' : ''For Liouville's equation in Euclidean space, see Liouville–Bratu–Gelfand equation.'' In differential geometry, Liouville's equation, named after Joseph Liouville, is the nonlinear partial differential equation satisfied by the conformal factor of a metric on a surface of constant Gaussian curvature : :\Delta_0\log f = -K f^2, where is the flat Laplace operator :\Delta_0 = \frac +\frac = 4 \frac \frac. Liouville's equation appears in the study of isothermal coordinates in differential geometry: the independent variables are the coordinates, while can be described as the conformal factor with respect to the flat metric. Occasionally it is the square that is referred to as the conformal factor, instead of itself. Liouville's equation was also taken as an example by David Hilbert in the formula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson. Statement of the equation Poisson's equation is \Delta\varphi = f where \Delta is the Laplace operator, and f and \varphi are real or complex-valued functions on a manifold. Usually, f is given and \varphi is sought. When the manifold is Euclidean space, the Laplace operator is often denoted as and so Poisson's equation is frequently written as \nabla^2 \varphi = f. In three-dimensional Cartesian coordinates, it takes the form \left( \frac + \frac + \frac \right)\va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Liouville
Joseph Liouville (; ; 24 March 1809 – 8 September 1882) was a French mathematician and engineer. Life and work He was born in Saint-Omer in France on 24 March 1809. His parents were Claude-Joseph Liouville (an army officer) and Thérèse Liouville (née Balland). Liouville gained admission into the École Polytechnique in 1825 and graduated in 1827. Just like Augustin-Louis Cauchy before him, Liouville studied engineering at École des Ponts et Chaussées after graduating from the Polytechnique, but opted instead for a career in mathematics. After some years as an assistant at various institutions including the École Centrale Paris, he was appointed as professor at the École Polytechnique in 1838. He obtained a chair in mathematics at the Collège de France in 1850 and a chair in mechanics at the Faculté des Sciences in 1857. Besides his academic achievements, he was very talented in organisational matters. Liouville founded the ''Journal de Mathématiques Pures et Ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand ( yi, ישראל געלפֿאַנד, russian: Изра́иль Моисе́евич Гельфа́нд, uk, Ізраїль Мойсейович Гельфанд; – 5 October 2009) was a prominent Soviet-American mathematician. He made significant contributions to many branches of mathematics, including group theory, representation theory and functional analysis. The recipient of many awards, including the Order of Lenin and the first Wolf Prize, he was a Foreign Fellow of the Royal Society and professor at Moscow State University and, after immigrating to the United States shortly before his 76th birthday, at Rutgers University. Gelfand is also a 1994 MacArthur Fellow. His legacy continues through his students, who include Endre Szemerédi, Alexandre Kirillov, Edward Frenkel, Joseph Bernstein, David Kazhdan, as well as his own son, Sergei Gelfand. Early years A native of Kherson G ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
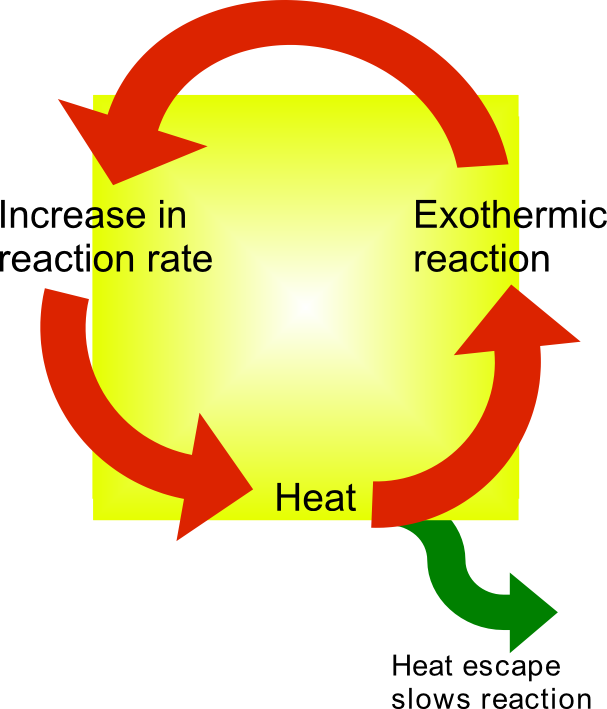
Thermal Runaway
Thermal runaway describes a process that is accelerated by increased temperature, in turn releasing energy that further increases temperature. Thermal runaway occurs in situations where an increase in temperature changes the conditions in a way that causes a further increase in temperature, often leading to a destructive result. It is a kind of uncontrolled positive feedback. In chemistry (and chemical engineering), thermal runaway is associated with strongly exothermic reactions that are accelerated by temperature rise. In electrical engineering, thermal runaway is typically associated with increased current flow and power dissipation. Thermal runaway can occur in civil engineering, notably when the heat released by large amounts of curing concrete is not controlled. In astrophysics, runaway nuclear fusion reactions in stars can lead to nova and several types of supernova explosions, and also occur as a less dramatic event in the normal evolution of solar-mass stars, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frank-Kamenetskii Theory
In combustion, Frank-Kamenetskii theory explains the thermal explosion of a homogeneous mixture of reactants, kept inside a closed vessel with constant temperature walls. It is named after a Russian scientist David A. Frank-Kamenetskii, who along with Nikolay Semenov developed the theory in the 1930s. Problem description Sources: Consider a vessel maintained at a constant temperature T_o, containing a homogeneous reacting mixture. Let the characteristic size of the vessel be a. Since the mixture is homogeneous, the density \rho is constant. During the initial period of ignition, the consumption of reactant concentration is negligible (see t_f and t_e below), thus the explosion is governed only by the energy equation. Assuming a one-step global reaction \text + \text \rightarrow \text + q, where q is the amount of heat released per unit mass of fuel consumed, and a reaction rate governed by Arrhenius law, the energy equation becomes :\rho c_v \frac = \lambda \nabla^2 T + q \rho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrophysics
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline said, Astrophysics "seeks to ascertain the nature of the heavenly bodies, rather than their positions or motions in space–''what'' they are, rather than ''where'' they are." Among the subjects studied are the Sun, other stars, galaxies, extrasolar planets, the interstellar medium and the cosmic microwave background. Emissions from these objects are examined across all parts of the electromagnetic spectrum, and the properties examined include luminosity, density, temperature, and chemical composition. Because astrophysics is a very broad subject, ''astrophysicists'' apply concepts and methods from many disciplines of physics, including classical mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum mechanics, relativity, nuclear and particle physics, and atomic a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Emden–Chandrasekhar Equation
In astrophysics, the Emden–Chandrasekhar equation is a dimensionless form of the Poisson equation for the density distribution of a spherically symmetric isothermal gas sphere subjected to its own gravitational force, named after Robert Emden and Subrahmanyan Chandrasekhar. The equation was first introduced by Robert Emden in 1907. The equation reads :\frac \frac\left(\xi^2 \frac\right)= e^ where \xi is the dimensionless radius and \psi is the related to the density of the gas sphere as \rho=\rho_c e^, where \rho_c is the density of the gas at the centre. The equation has no known explicit solution. If a polytropic fluid is used instead of an isothermal fluid, one obtains the Lane–Emden equation. The isothermal assumption is usually modeled to describe the core of a star. The equation is solved with the initial conditions, :\psi =0, \quad \frac =0 \quad \text \quad \xi=0. The equation appears in other branches of physics as well, for example the same equation appears in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planetary Nebula
A planetary nebula (PN, plural PNe) is a type of emission nebula consisting of an expanding, glowing shell of ionized gas ejected from red giant stars late in their lives. The term "planetary nebula" is a misnomer because they are unrelated to planets. The term originates from the planet-like round shape of these nebulae observed by astronomers through early telescopes. The first usage may have occurred during the 1780s with the English astronomer William Herschel who described these nebulae as resembling planets; however, as early as January 1779, the French astronomer Antoine Darquier de Pellepoix described in his observations of the Ring Nebula, "very dim but perfectly outlined; it is as large as Jupiter and resembles a fading planet". Though the modern interpretation is different, the old term is still used. All planetary nebulae form at the end of the life of a star of intermediate mass, about 1-8 solar masses. It is expected that the Sun will form a planetary nebu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if its Taylor series about ''x''0 converges to the function in some neighborhood for every ''x''0 in its domain. Definitions Formally, a function f is ''real analytic'' on an open set D in the real line if for any x_0\in D one can write : f(x) = \sum_^\infty a_ \left( x-x_0 \right)^ = a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + a_3 (x-x_0)^3 + \cdots in which the coefficients a_0, a_1, \dots are real numbers and the series is convergent to f(x) for x in a neighborhood of x_0. Alternatively, a real analytic function is an infinitely differentiable function such that the Taylor series at any point x_0 in its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel D
Daniel is a masculine given name and a surname of Hebrew origin. It means "God is my judge"Hanks, Hardcastle and Hodges, ''Oxford Dictionary of First Names'', Oxford University Press, 2nd edition, , p. 68. (cf. Gabriel—"God is my strength"), and derives from two early biblical figures, primary among them Daniel from the Book of Daniel. It is a common given name for males, and is also used as a surname. It is also the basis for various derived given names and surnames. Background The name evolved into over 100 different spellings in countries around the world. Nicknames ( Dan, Danny) are common in both English and Hebrew; "Dan" may also be a complete given name rather than a nickname. The name "Daniil" (Даниил) is common in Russia. Feminine versions ( Danielle, Danièle, Daniela, Daniella, Dani, Danitza) are prevalent as well. It has been particularly well-used in Ireland. The Dutch names "Daan" and "Daniël" are also variations of Daniel. A related surname de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |