|
Eigenform
In mathematics, an eigenform (meaning simultaneous Hecke eigenform with modular group SL(2,Z)) is a modular form which is an eigenvector for all Hecke operators ''Tm'', ''m'' = 1, 2, 3, .... Eigenforms fall into the realm of number theory, but can be found in other areas of math and science such as analysis, combinatorics, and physics. A common example of an eigenform, and the only non-cuspidal eigenforms, are the Eisenstein series. Another example is the Δ Function. In second-order cybernetics, eigenforms are an example of a self-referential system.Kauffman, L. H. (2003). Eigenforms: Objects as tokens for eigenbehaviors. Cybernetics and Human Knowing, 10(3/4), 73-90. Normalization There are two different normalizations for an eigenform (or for a modular form in general). Algebraic normalization An eigenform is said to be normalized when scaled so that the ''q''-coefficient in its Fourier series is one: :f = a_0 + q + \sum_^\infty a_i q^i wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
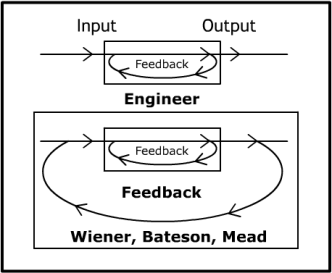
Second-order Cybernetics
Second-order cybernetics, also known as the cybernetics of cybernetics, is the recursive application of cybernetics to itself and the reflexive practice of cybernetics according to such a critique. It is cybernetics where "the role of the observer is appreciated and acknowledged rather than disguised, as had become traditional in western science". Glanville, R. (2002). "Second order cybernetics." In F. Parra-Luna (ed.), Systems science and cybernetics. In ''Encyclopaedia of Life Support Systems'' (EOLSS). OxfordEoLSS Second-order cybernetics was developed between the late 1960s and mid 1970s by Heinz von Foerster and others, with key inspiration coming from Margaret Mead. Foerster referred to it as "the control of control and the communication of communication" and differentiated first order cybernetics as "the cybernetics of observed systems" and second-order cybernetics as "the cybernetics of observing systems". Foerster, Heinz von, ed. ''Cybernetics of Cybernetics: Or, the Contro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second-order Cybernetics
Second-order cybernetics, also known as the cybernetics of cybernetics, is the recursive application of cybernetics to itself and the reflexive practice of cybernetics according to such a critique. It is cybernetics where "the role of the observer is appreciated and acknowledged rather than disguised, as had become traditional in western science". Glanville, R. (2002). "Second order cybernetics." In F. Parra-Luna (ed.), Systems science and cybernetics. In ''Encyclopaedia of Life Support Systems'' (EOLSS). OxfordEoLSS Second-order cybernetics was developed between the late 1960s and mid 1970s by Heinz von Foerster and others, with key inspiration coming from Margaret Mead. Foerster referred to it as "the control of control and the communication of communication" and differentiated first order cybernetics as "the cybernetics of observed systems" and second-order cybernetics as "the cybernetics of observing systems". Foerster, Heinz von, ed. ''Cybernetics of Cybernetics: Or, the Contro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cybernetics
Cybernetics is a wide-ranging field concerned with circular causality, such as feedback, in regulatory and purposive systems. Cybernetics is named after an example of circular causal feedback, that of steering a ship, where the helmsperson maintains a steady course in a changing environment by adjusting their steering in continual response to the effect it is observed as having. Cybernetics is concerned with circular causal processes such as steering however they are embodied,Ashby, W. R. (1956). An introduction to cybernetics. London: Chapman & Hall, p. 1. including in ecological, technological, biological, cognitive, and social systems, and in the context of practical activities such as designing, learning, managing, conversation, and the practice of cybernetics itself. Cybernetics' transdisciplinary and "antidisciplinary" character has meant that it intersects with a number of other fields, leading to it having both wide influence and diverse interpretations. Cybernetics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hecke Operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations. History used Hecke operators on modular forms in a paper on the special cusp form of Ramanujan, ahead of the general theory given by . Mordell proved that the Ramanujan tau function, expressing the coefficients of the Ramanujan form, : \Delta(z)=q\left(\prod_^(1-q^n)\right)^= \sum_^ \tau(n)q^n, \quad q=e^, is a multiplicative function: : \tau(mn)=\tau(m)\tau(n) \quad \text (m,n)=1. The idea goes back to earlier work of Adolf Hurwitz, who treated algebraic correspondences between modular curves which realise some individual Hecke operators. Mathematical description Hecke operators can be realized in a number of contexts. The simplest meaning is combinatorial, namely as taking for a given integer some functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Form
In mathematics, a modular form is a (complex) analytic function on the upper half-plane satisfying a certain kind of functional equation with respect to the Group action (mathematics), group action of the modular group, and also satisfying a growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections with number theory. Modular forms appear in other areas, such as algebraic topology, sphere packing, and string theory. A modular function is a function that is invariant with respect to the modular group, but without the condition that be Holomorphic function, holomorphic in the upper half-plane (among other requirements). Instead, modular functions are Meromorphic function, meromorphic (that is, they are holomorphic on the complement of a set of isolated points, which are poles of the function). Modular form theory is a special case of the more general theory of automorphic form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heinz Von Foerster
Heinz von Foerster (German spelling: Heinz von Förster; November 13, 1911 – October 2, 2002) was an Austrian American scientist combining physics and philosophy, and widely attributed as the originator of Second-order cybernetics. He was twice a Guggenheim fellow (1956–57 and 1963–64) and also was a fellow of the American Association for the Advancement of Science, 1980. He is well known for his 1960 Doomsday equation formula published in ''Science'' predicting future population growth. As a polymath, he wrote nearly two hundred professional papers, gaining renown in fields from computer science and artificial intelligence to epistemology, and researched high-speed electronics and electro-optics switching devices as a physicist, and in biophysics, the study of memory and knowledge. He worked on cognition based on neurophysiology, mathematics, and philosophy and was called "one of the most consequential thinkers in the history of cybernetics". He came to the United States, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Group
In mathematics, the modular group is the projective special linear group of matrices with integer coefficients and determinant 1. The matrices and are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic. Definition The modular group is the group of linear fractional transformations of the upper half of the complex plane, which have the form :z\mapsto\frac, where , , , are integers, and . The group operation is function composition. This group of transformations is isomorphic to the projective special linear group , which is the quotient of the 2-dimensional special linear group over the integers by its center . In other words, consists of all matrices :\begin a & b \\ c & d \end where , , , are integers, , and pairs of matrices and are considered to be identical. The group operation is the usual mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petersson Inner Product
In mathematics the Petersson inner product is an inner product defined on the space of entire modular forms. It was introduced by the German mathematician Hans Petersson. Definition Let \mathbb_k be the space of entire modular forms of weight k and \mathbb_k the space of cusp forms. The mapping \langle \cdot , \cdot \rangle : \mathbb_k \times \mathbb_k \rightarrow \mathbb, :\langle f , g \rangle := \int_\mathrm f(\tau) \overline (\operatorname\tau)^k d\nu (\tau) is called Petersson inner product, where :\mathrm = \left\ is a fundamental region of the modular group \Gamma and for \tau = x + iy :d\nu(\tau) = y^dxdy is the hyperbolic volume form. Properties The integral is absolutely convergent and the Petersson inner product is a positive definite Hermitian form. For the Hecke operators T_n, and for forms f,g of level \Gamma_0, we have: :\langle T_n f , g \rangle = \langle f , T_n g \rangle This can be used to show that the space of cusp forms of level \Gamma_0 has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or ''period''), the number of components, and their amplitudes and phase parameters. With appropriate choices, one cycle (or ''period'') of the summation can be made to approximate an arbitrary function in that interval (or the entire function if it too is periodic). The number of components is theoretically infinite, in which case the other parameters can be chosen to cause the series to converge to almost any ''well behaved'' periodic function (see Pathological and Dirichlet–Jordan test). The components of a particular function are determined by ''analysis'' techniques described in this article. Sometimes the components are known first, and the unknown function is ''synthesized'' by a Fourier series. Such is the case of a discrete-ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass's Elliptic Functions
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by the symbol ℘, a uniquely fancy script ''p''. They play an important role in the theory of elliptic functions. A ℘-function together with its derivative can be used to parameterize elliptic curves and they generate the field of elliptic functions with respect to a given period lattice. Symbol for Weierstrass \wp-function Definition Let \omega_1,\omega_2\in\mathbb be two complex numbers that are linearly independent over \mathbb and let \Lambda:=\mathbb\omega_1+\mathbb\omega_2:=\ be the lattice generated by those numbers. Then the \wp-function is defined as follows: \weierp(z,\omega_1,\omega_2):=\weierp(z,\Lambda) := \frac + \sum_\left(\frac 1 - \frac 1 \right). This series converges locally uniformly absolutely in \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvector
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eisenstein Series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly. Originally defined for the modular group, Eisenstein series can be generalized in the theory of automorphic forms. Eisenstein series for the modular group Let be a complex number with strictly positive imaginary part. Define the holomorphic Eisenstein series of weight , where is an integer, by the following series: :G_(\tau) = \sum_ \frac. This series absolutely converges to a holomorphic function of in the upper half-plane and its Fourier expansion given below shows that it extends to a holomorphic function at . It is a remarkable fact that the Eisenstein series is a modular form. Indeed, the key property is its -invariance. Explicitly if and then :G_ \left( \frac \right) = (c\tau +d)^ G_(\tau) Relation to modular invariants The modular invariants and of an elliptic curve are given by the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
