|
Diffusion Map Of A Torodial Helix
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer. Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called ''centigrade''), the Fahrenheit scale (°F), and the Kelvin scale (K), the latter being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI). Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible to extract energy as heat from a body at that temperature. Temperature is important in all fields of na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Impulse Response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time (or possibly as a function of some other independent variable that parameterizes the dynamic behavior of the system). In all these cases, the dynamic system and its impulse response may be actual physical objects, or may be mathematical systems of equations describing such objects. Since the impulse function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function has), the impulse response defines the response of a linear time-invariant system for all frequencies. Mathematical considerat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brownian Motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas). This pattern of motion typically consists of random fluctuations in a particle's position inside a fluid sub-domain, followed by a relocation to another sub-domain. Each relocation is followed by more fluctuations within the new closed volume. This pattern describes a fluid at thermal equilibrium, defined by a given temperature. Within such a fluid, there exists no preferential direction of flow (as in transport phenomena). More specifically, the fluid's overall linear and angular momenta remain null over time. The kinetic energies of the molecular Brownian motions, together with those of molecular rotations and vibrations, sum up to the caloric component of a fluid's internal energy (the equipartition theorem). This motion is named after the botanist Robert Brown, who first described the phenomenon in 1827, while looking th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anomalous Diffusion
Anomalous diffusion is a diffusion process with a non-linear relationship between the mean squared displacement (MSD), \langle r^(\tau )\rangle , and time. This behavior is in stark contrast to Brownian motion, the typical diffusion process described by Einstein and Smoluchowski, where the MSD is linear in time (namely, \langle r^(\tau )\rangle =2dD\tau with ''d'' being the number of dimensions and ''D'' the diffusion coefficient). Examples of anomalous diffusion in nature have been observed in biology in the cell nucleus, plasma membrane and cytoplasm. Unlike typical diffusion, anomalous diffusion is described by a power law, \langle r^(\tau )\rangle =K_\alpha\tau^\alphawhere K_\alpha is the so-called generalized diffusion coefficient and \tau is the elapsed time. In Brownian motion, α = 1. If α > 1, the process is superdiffusive. Superdiffusion can be the result of active cellular transport processes or due to jumps with a heavy-tail distribution. If α < 1, the parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fick's Laws Of Diffusion
Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation. A diffusion process that obeys Fick's laws is called normal or Fickian diffusion; otherwise, it is called anomalous diffusion or non-Fickian diffusion. History In 1855, physiologist Adolf Fick first reported* * his now well-known laws governing the transport of mass through diffusive means. Fick's work was inspired by the earlier experiments of Thomas Graham, which fell short of proposing the fundamental laws for which Fick would become famous. Fick's law is analogous to the relationships discovered at the same epoch by other eminent scientists: Darcy's law (hydraulic flow), Ohm's law (charge transport), and Fourier's Law (heat transport). Fick's experiments (modeled on Graham's) dealt with measuring the concentration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others. The fundamental analysis in all three subfields of mass, heat, and momentum transfer are often grounded in the simple principle that the total sum of the quantities being studied must be conserved by the system and its environment. Thus, the different phenomena that lead to transport are each considered individually with the knowled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
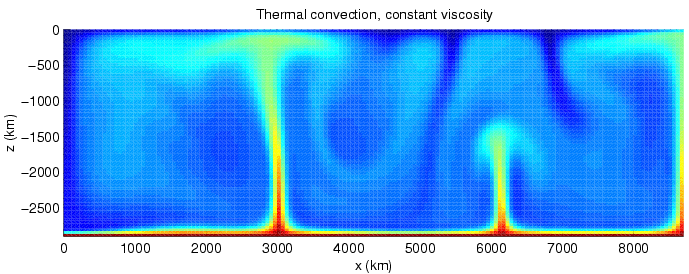
Convection
Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be transient (such as when a multiphase mixture of oil and water separates) or steady state (see Convection cell). The convection may be due to gravitational, electromagnetic or fictitious body forces. Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its mantle. Discrete convective cells in the atmosphere can be identified by clouds, with stronger convection resulting in thunderstorms. Natural convection also plays a role in stellar physics. Convection is often cate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Gamble Kirkwood
John "Jack" Gamble Kirkwood (May 30, 1907, Gotebo, Oklahoma – August 9, 1959, New Haven, Connecticut) was a noted chemist and physicist, holding faculty positions at Cornell University, the University of Chicago, California Institute of Technology, and Yale University. Early life and background Kirkwood was born in Gotebo, Oklahoma, the oldest child of John Millard and Lillian Gamble Kirkwood. His father was educated as an attorney and was a distributor for the Goodyear Corporation in the state of Kansas. In addition to Jack Kirkwood, there were two younger sisters: Caroline (1910) and Margaret (1921). In 1909, the family moved to Wichita, Kansas. In the 1920s the family traveled to Pasadena, California to escape Midwestern winters. Education While in Pasadena, Kirkwood, age 15, audited chemistry classes at Caltech. Showing remarkable talent in mathematics and chemistry, Kirkwood was persuaded by A. A. Noyes to enroll at Caltech before finishing his high school education ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advection
In the field of physics, engineering, and earth sciences, advection is the transport of a substance or quantity by bulk motion of a fluid. The properties of that substance are carried with it. Generally the majority of the advected substance is also a fluid. The properties that are carried with the advected substance are conserved properties such as energy. An example of advection is the transport of pollutants or silt in a river by bulk water flow downstream. Another commonly advected quantity is energy or enthalpy. Here the fluid may be any material that contains thermal energy, such as water or air. In general, any substance or conserved, extensive quantity can be advected by a fluid that can hold or contain the quantity or substance. During advection, a fluid transports some conserved quantity or material via bulk motion. The fluid's motion is described mathematically as a vector field, and the transported material is described by a scalar field showing its distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Lattice random walk A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the Roman Republic it became the dominant language in the Italian region and subsequently throughout the Roman Empire. Even after the fall of Western Rome, Latin remained the common language of international communication, science, scholarship and academia in Europe until well into the 18th century, when other regional vernaculars (including its own descendants, the Romance languages) supplanted it in common academic and political usage, and it eventually became a dead language in the modern linguistic definition. Latin is a highly inflected language, with three distinct genders (masculine, feminine, and neuter), six or seven noun cases (nominative, accusative, genitive, dative, ablative, and vocative), five declensions, four ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |