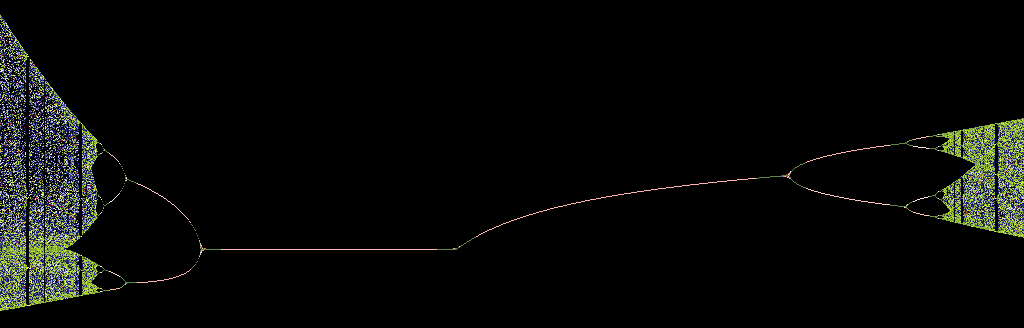
|
Bogdanov–Takens Bifurcation
In bifurcation theory, a field within mathematics, a Bogdanov–Takens bifurcation is a well-studied example of a bifurcation with co-dimension two, meaning that two parameters must be varied for the bifurcation to occur. It is named after Rifkat Bogdanov and Floris Takens, who independently and simultaneously described this bifurcation. A system ''y = ''f''(''y'') undergoes a Bogdanov–Takens bifurcation if it has a fixed point and the linearization of ''f'' around that point has a double eigenvalue at zero (assuming that some technical nondegeneracy conditions are satisfied). Three codimension-one bifurcations occur nearby: a saddle-node bifurcation, an Andronov–Hopf bifurcation and a homoclinic bifurcation Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Mo .... All associated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bogdanov Takens Bifurcation
Bogdanov (Богданов) or Bogdanova (Богданова; feminine) is a common Russian surname that derives from the given name Bogdan and literally means ''Bogdan's''. Translated: Bogu dan = God gave. Notable people with the surname include: Bogdanov *Abraham Bogdanove (1888–1946) Russian muralist, artist and educator *Alexei Alexeivich Bogdanov (1907–1971), Soviet geologist * Andrei Ivanovich Bogdanov (1692–1766), Russian bibliographer and ethnographer *Igor and Grichka Bogdanoff (1949–2021/2022), French TV hosts and twin brothers, notable for the Bogdanov affair and numerous internet memes *Ivan Bogdanov (1897–1942), Soviet military officer *Ivan Bogdanov (painter) (1855–1932), Russian painter *Malachi Bogdanov, British theatre director *Michael Bogdanov (1938–2017), British theatre director * Mikhail Aleksandrovich Bogdanov (1914–1995), Soviet production designer *Nikolay Bogdanov-Belsky (1868–1945), Russian painter * Semen llyich Bogdanov (1894–1960), S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bifurcations, which can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Co-dimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, to submanifolds in manifolds, and suitable subsets of algebraic varieties. For affine and projective algebraic varieties, the codimension equals the height of the defining ideal. For this reason, the height of an ideal is often called its codimension. The dual concept is relative dimension. Definition Codimension is a ''relative'' concept: it is only defined for one object ''inside'' another. There is no “codimension of a vector space (in isolation)”, only the codimension of a vector ''sub''space. If ''W'' is a linear subspace of a finite-dimensional vector space ''V'', then the codimension of ''W'' in ''V'' is the difference between the dimensions: :\operatorname(W) = \dim(V) - \dim(W). It is the complement of the dimension of ''W,'' in that, with the dimension of ''W,'' it adds up to the dimension of the ambient space ''V:'' :\dim(W) + \operatorname(W) = \dim(V). Similarl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rifkat Bogdanov
Rifkat Ibragimovich Bogdanov (russian: Рифка́т Ибраги́мович Богда́нов; June 13, 1950 – November 3, 2013) was a Soviet and Russian mathematician known for contributions to nonlinear dynamical systems, bifurcation theory, and differential geometry. He was an ethnic Tatar. In his work on bifurcations of limit cycles and versal deformations of singular points of vector fields (1975–76), he described a bifurcation of co-dimension 2, which has become known in the literature as the Bogdanov–Takens bifurcation. Born in the village of Mamykovo in Tatarstan, Bogdanov had a doctorate in physico-mathematical sciences and was a professor in two Russian research organizations: the Skobeltsyn Institute of Nuclear Physics at Lomonosov Moscow State University and the Department of Higher Mathematics at MATI — the Tsiolkovskii State Technological University. See also * Bogdanov–Takens bifurcation Selected publications * R. I. Bogdanov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floris Takens
Floris Takens (12 November 1940 – 20 June 2010) was a Dutch mathematician known for contributions to the theory of chaotic dynamical systems. Together with David Ruelle, he predicted that fluid turbulence could develop through a strange attractor, a term they coined, as opposed to the then-prevailing theory of accretion of modes. The prediction was later confirmed by experiment. Takens also established the result now known as the Takens's theorem, which shows how to reconstruct a dynamical system from an observed time-series. He was the first to show how chaotic attractors could be learned by neural networks. Takens was born in Zaandam in the Netherlands. He attended schools in The Hague and in Zaandam before serving in the Dutch army for one year (1960–1961). At the University of Amsterdam he concluded his undergraduate and graduate studies. He was granted a doctorate in mathematics in 1969 under the supervision of Nicolaas Kuiper for a thesis entitled ''The minimal number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic roo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle-node Bifurcation
In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed points (or equilibria) of a dynamical system collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue sky bifurcation in reference to the sudden creation of two fixed points. If the phase space is one-dimensional, one of the equilibrium points is unstable (the saddle), while the other is stable (the node). Saddle-node bifurcations may be associated with hysteresis loops and catastrophes. Normal form A typical example of a differential equation with a saddle-node bifurcation is: :\frac=r+x^2. Here x is the state variable and r is the bifurcation parameter. *If r0 there are no equilibrium points. In fact, this is a normal fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andronov–Hopf Bifurcation
In the mathematical theory of bifurcations, a Hopf bifurcation is a critical point where a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis. Under reasonably generic assumptions about the dynamical system, a small-amplitude limit cycle branches from the fixed point. A Hopf bifurcation is also known as a Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Aleksandr Andronov and Eberhard Hopf. Overview Supercritical and subcritical Hopf bifurcations The limit cycle is orbitally stable if a specific quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it is unstable and the bifurcation is subcritical. The normal form of a Hopf bifurcation is: ::\f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homoclinic Bifurcation
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bifurcations, which can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Form (bifurcation Theory)
In mathematics, the normal form of a dynamical system is a simplified form that can be useful in determining the system's behavior. Normal forms are often used for determining local bifurcations in a system. All systems exhibiting a certain type of bifurcation are locally (around the equilibrium) topologically equivalent to the normal form of the bifurcation. For example, the normal form of a saddle-node bifurcation is : \frac = \mu + x^2 where \mu is the bifurcation parameter. The transcritical bifurcation : \frac = r \ln x + x - 1 near x=1 can be converted to the normal form : \frac = \mu u - u^2 + O(u^3) with the transformation u = x -1, \mu = r + 1 .Strogatz, Steven. "Nonlinear Dynamics and Chaos". Westview Press, 2001. p. 52. See also canonical form In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |