|
Saddle-node Bifurcation
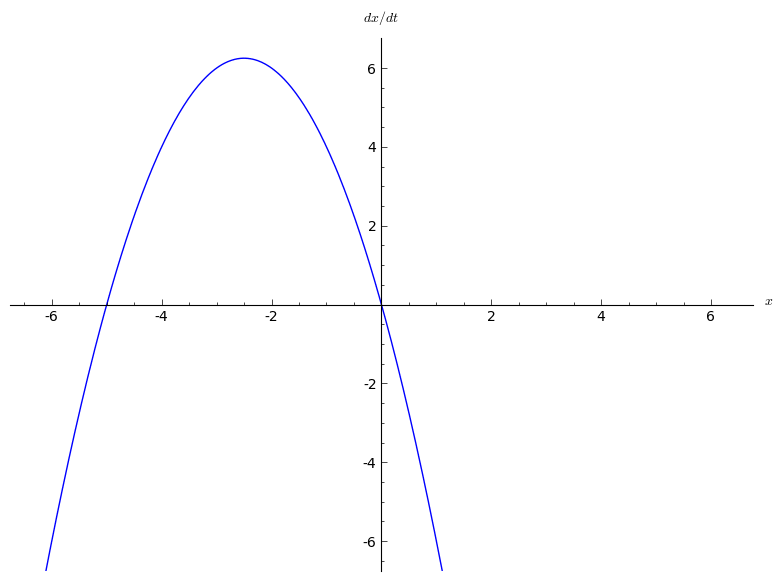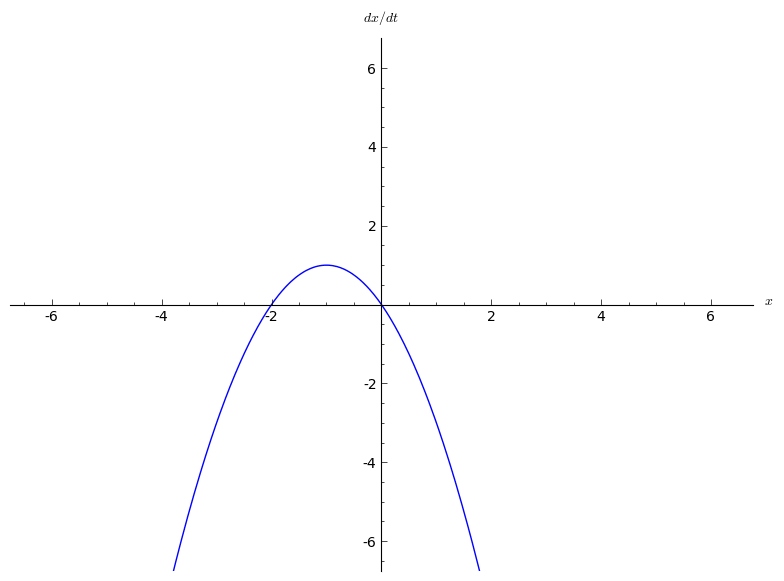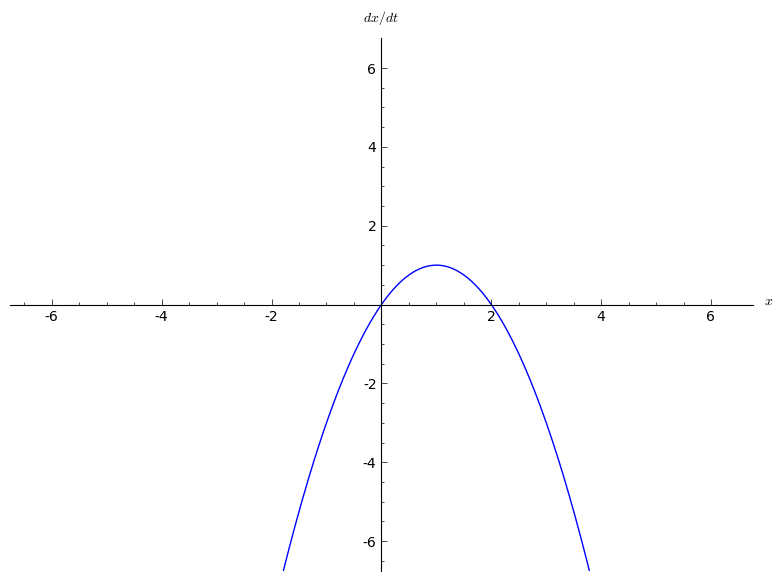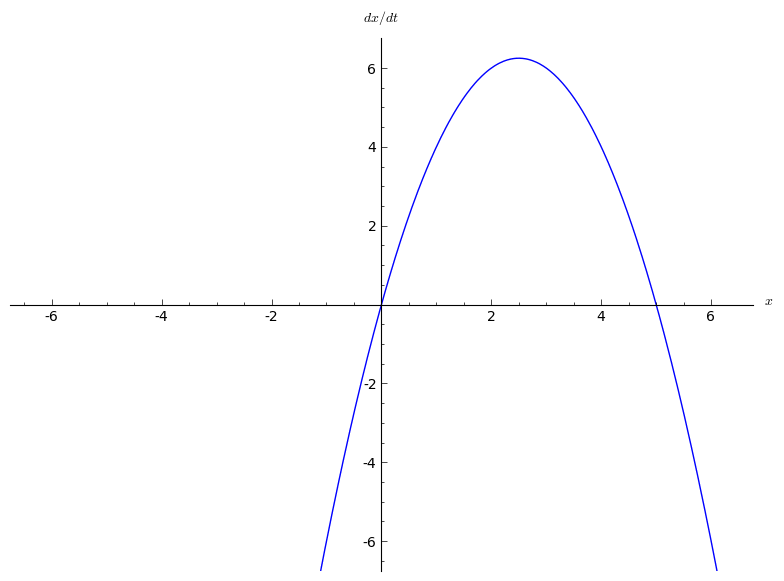
In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed points (or equilibria) of a dynamical system collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue sky bifurcation in reference to the sudden creation of two fixed points. If the phase space is one-dimensional, one of the equilibrium points is unstable (the saddle), while the other is stable (the node). Saddle-node bifurcations may be associated with hysteresis loops and catastrophes. Normal form A typical example of a differential equation with a saddle-node bifurcation is: :\frac=r+x^2. Here x is the state variable and r is the bifurcation parameter. *If r0 there are no equilibrium points. In fact, this is a normal fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Conjugacy
In mathematics, two functions are said to be topologically conjugate if there exists a homeomorphism that will conjugate the one into the other. Topological conjugacy, and related-but-distinct of flows, are important in the study of iterated functions and more generally dynamical systems, since, if the dynamics of one iterative function can be determined, then that for a topologically conjugate function follows trivially. To illustrate this directly: suppose that f and g are iterated functions, and there exists a homeomorphism h such that :g = h^ \circ f \circ h, so that f and g are topologically conjugate. Then one must have :g^n = h^ \circ f^n \circ h, and so the iterated systems are topologically conjugate as well. Here, \circ denotes function composition. Definition f\colon X \to X, g\colon Y \to Y, and h\colon Y \to X are continuous functions on topological spaces, X and Y. f being topologically semiconjugate to g means, by definition, that h is a surjection such t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Point
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface that ''curves up'' in one direction, and ''curves down'' in a different direction, resembling a riding saddle or a mountain pass between two peaks forming a landform saddle. In te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hopf Bifurcation
In the mathematical theory of bifurcations, a Hopf bifurcation is a critical point where a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis. Under reasonably generic assumptions about the dynamical system, a small-amplitude limit cycle branches from the fixed point. A Hopf bifurcation is also known as a Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Aleksandr Andronov and Eberhard Hopf. Overview Supercritical and subcritical Hopf bifurcations The limit cycle is orbitally stable if a specific quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it is unstable and the bifurcation is subcritical. The normal form of a Hopf bifurcation is: ::\frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcritical Bifurcation
In bifurcation theory, a field within mathematics, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized by an equilibrium having an eigenvalue whose real part passes through zero. A transcritical bifurcation is one in which a fixed point exists for all values of a parameter and is never destroyed. However, such a fixed point interchanges its stability with another fixed point as the parameter is varied. In other words, both before and after the bifurcation, there is one unstable and one stable fixed point. However, their stability is exchanged when they collide. So the unstable fixed point becomes stable and vice versa. The normal form of a transcritical bifurcation is :\frac = rx - x^2. This equation is similar to the logistic equation A logistic function or logistic curve is a common S-shaped curve (sigmoid curve) with equation f(x) = \frac, where For values of x in the domain of real numbers from -\infty to +\inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pitchfork Bifurcation
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation where the system transitions from one fixed point to three fixed points. Pitchfork bifurcations, like Hopf bifurcations, have two types – supercritical and subcritical. In continuous dynamical systems described by ODEs—i.e. flows—pitchfork bifurcations occur generically in systems with symmetry. Supercritical case The normal form of the supercritical pitchfork bifurcation is : \frac=rx-x^3. For r0 there is an unstable equilibrium at x = 0, and two stable equilibria at x = \pm\sqrt. Subcritical case The normal form for the subcritical case is : \frac=rx+x^3. In this case, for r0 the equilibrium at x=0 is unstable. Formal definition An ODE : \dot=f(x,r)\, described by a one parameter function f(x, r) with r \in \mathbb satisfying: : -f(x, r) = f(-x, r)\,\, (f is an odd function), :\begin \frac(0, r_0) &= 0, & \frac(0, r_0) &= 0, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcritical Bifurcation
In bifurcation theory, a field within mathematics, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized by an equilibrium having an eigenvalue whose real part passes through zero. A transcritical bifurcation is one in which a fixed point exists for all values of a parameter and is never destroyed. However, such a fixed point interchanges its stability with another fixed point as the parameter is varied. In other words, both before and after the bifurcation, there is one unstable and one stable fixed point. However, their stability is exchanged when they collide. So the unstable fixed point becomes stable and vice versa. The normal form of a transcritical bifurcation is :\frac = rx - x^2. This equation is similar to the logistic equation A logistic function or logistic curve is a common S-shaped curve (sigmoid curve) with equation f(x) = \frac, where For values of x in the domain of real numbers from -\infty to +\inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Point
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface that ''curves up'' in one direction, and ''curves down'' in a different direction, resembling a riding saddle or a mountain pass between two peaks forming a landform saddle. In te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Form (bifurcation Theory)
In mathematics, the normal form of a dynamical system is a simplified form that can be useful in determining the system's behavior. Normal forms are often used for determining local bifurcations in a system. All systems exhibiting a certain type of bifurcation are locally (around the equilibrium) topologically equivalent to the normal form of the bifurcation. For example, the normal form of a saddle-node bifurcation is : \frac = \mu + x^2 where \mu is the bifurcation parameter. The transcritical bifurcation : \frac = r \ln x + x - 1 near x=1 can be converted to the normal form : \frac = \mu u - u^2 + O(u^3) with the transformation u = x -1, \mu = r + 1 .Strogatz, Steven. "Nonlinear Dynamics and Chaos". Westview Press, 2001. p. 52. See also canonical form In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bifurcations, which can b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fold Bifurcation
In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed points (or equilibria) of a dynamical system collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue sky bifurcation in reference to the sudden creation of two fixed points. If the phase space is one-dimensional, one of the equilibrium points is unstable (the saddle), while the other is stable (the node). Saddle-node bifurcations may be associated with hysteresis loops and catastrophes. Normal form A typical example of a differential equation with a saddle-node bifurcation is: :\frac=r+x^2. Here x is the state variable and r is the bifurcation parameter. *If r0 there are no equilibrium points. In fact, this is a normal fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
