Andronov–Hopf Bifurcation on:
[Wikipedia]
[Google]
[Amazon]
 In the mathematical theory of bifurcations, a Hopf bifurcation is a critical point where a system's stability switches and a
In the mathematical theory of bifurcations, a Hopf bifurcation is a critical point where a system's stability switches and a
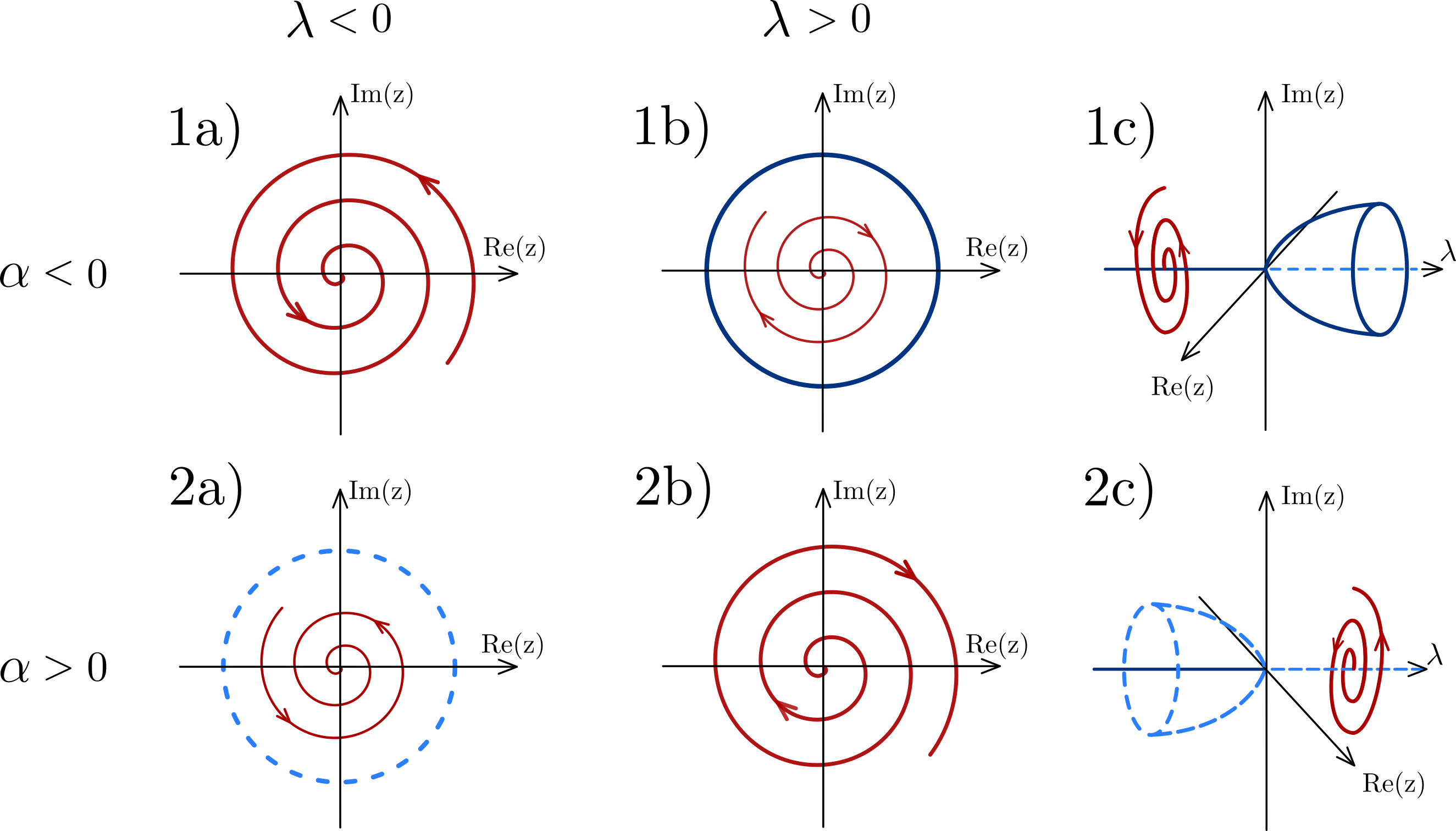 The limit cycle is orbitally stable if a specific quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it is unstable and the bifurcation is subcritical.
The normal form of a Hopf bifurcation is:
:: where ''z'', ''b'' are both complex and ''λ'' is a parameter.
Write: The number ''α'' is called the first
The limit cycle is orbitally stable if a specific quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it is unstable and the bifurcation is subcritical.
The normal form of a Hopf bifurcation is:
:: where ''z'', ''b'' are both complex and ''λ'' is a parameter.
Write: The number ''α'' is called the first
The associated Sturm series is: : The Sturm polynomials can be written as (here ): : The above proposition 2 tells that one must have: : Because 1 > 0 and −1 < 0 are obvious, one can conclude that a Hopf bifurcation may occur for Van der Pol oscillator if .
The Hopf Bifurcation
Andronov–Hopf bifurcation page
at
 In the mathematical theory of bifurcations, a Hopf bifurcation is a critical point where a system's stability switches and a
In the mathematical theory of bifurcations, a Hopf bifurcation is a critical point where a system's stability switches and a periodic solution
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a ...
loses stability, as a pair of complex conjugate eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
s—of the linearization
In mathematics, linearization is finding the linear approximation to a function at a given point. The linear approximation of a function is the first order Taylor expansion around the point of interest. In the study of dynamical systems, lineariz ...
around the fixed point—crosses the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the ...
imaginary axis. Under reasonably generic assumptions about the dynamical system, a small-amplitude limit cycle branches from the fixed point.
A Hopf bifurcation is also known as a Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The ...
, Aleksandr Andronov
Aleksandr Aleksandrovich Andronov (russian: Алекса́ндр Алекса́ндрович Андро́нов; , Moscow – October 31, 1952, Gorky) was a Soviet physicist and member of the Soviet Academy of Sciences (1946). He worked exten ...
and Eberhard Hopf.
Overview
Supercritical and subcritical Hopf bifurcations
 The limit cycle is orbitally stable if a specific quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it is unstable and the bifurcation is subcritical.
The normal form of a Hopf bifurcation is:
:: where ''z'', ''b'' are both complex and ''λ'' is a parameter.
Write: The number ''α'' is called the first
The limit cycle is orbitally stable if a specific quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it is unstable and the bifurcation is subcritical.
The normal form of a Hopf bifurcation is:
:: where ''z'', ''b'' are both complex and ''λ'' is a parameter.
Write: The number ''α'' is called the first Lyapunov Lyapunov (, in old-Russian often written Лепунов) is a Russian surname that is sometimes also romanized as Ljapunov, Liapunov or Ljapunow. Notable people with the surname include:
* Alexey Lyapunov (1911–1973), Russian mathematician
* Alek ...
coefficient.
* If ''α'' is negative then there is a stable limit cycle for ''λ'' > 0:
::
: where
::
: The bifurcation is then called supercritical.
* If ''α'' is positive then there is an unstable limit cycle for ''λ'' < 0. The bifurcation is called subcritical.
Intuition
The normal form of the supercritical Hopf bifurcation can be expressed intuitively in polar coordinates, : where is the instantaneous amplitude of the oscillation and is its instantaneous angular position. The angular velocity is fixed. When , the differential equation for has an unstable fixed point at and a stable fixed point at . The system thus describes a stable circular limit cycle with radius and angular velocity . When then is the only fixed point and it is stable. In that case, the system describes a spiral that converges to the origin.Cartesian coordinates
The polar coordinates can be transformed into Cartesian coordinates by writing and . Differentiating and with respect to time yields the differential equations, : and :Subcritical case
The normal form of the subcritical Hopf is obtained by negating the sign of , : which reverses the stability of the fixed points in . For the limit cycle is now unstable and the origin is stable.Example
Hopf bifurcations occur in the Lotka–Volterra model ofpredator–prey interaction
Predation is a biological interaction where one organism, the predator, kills and eats another organism, its prey. It is one of a family of common List of feeding behaviours, feeding behaviours that includes parasitism and micropredation (wh ...
(known as paradox of enrichment
The paradox of enrichment is a term from population ecology coined by Michael Rosenzweig in 1971. He described an effect in six predator–prey models where increasing the food available to the prey caused the predator's population to destabiliz ...
), the Hodgkin–Huxley model
The Hodgkin–Huxley model, or conductance-based model, is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is a set of nonlinear differential equations that approximates the electrical charact ...
for nerve membrane potential, the Selkov model of glycolysis
Glycolysis is the metabolic pathway that converts glucose () into pyruvate (). The free energy released in this process is used to form the high-energy molecules adenosine triphosphate (ATP) and reduced nicotinamide adenine dinucleotide (NADH ...
, the Belousov–Zhabotinsky reaction
A Belousov–Zhabotinsky reaction, or BZ reaction, is one of a class of reactions that serve as a classical example of non-equilibrium thermodynamics, resulting in the establishment of a nonlinear chemical oscillator. The only common element in ...
, the Lorenz attractor
The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lo ...
, the Brusselator
The Brusselator is a theoretical model for a type of autocatalytic reaction.
The Brusselator model was proposed by Ilya Prigogine and his collaborators at the Université Libre de Bruxelles.
It is a portmanteau of Brussels and oscillator.
...
, Classical electromagnetism. Hopf bifurcations have also been shown to occur in fission waves.
The Selkov model is
:
The phase portrait illustrating the Hopf bifurcation in the Selkov model is shown on the right.For detailed derivation, see
In railway vehicle systems, Hopf bifurcation analysis is notably important. Conventionally a railway vehicle's stable motion at low speeds crosses over to unstable at high speeds. One aim of the nonlinear analysis of these systems is to perform an analytical investigation of bifurcation, nonlinear lateral stability and hunting behavior of rail vehicles on a tangent track, which uses the Bogoliubov method.
Definition of a Hopf bifurcation
The appearance or the disappearance of a periodic orbit through a local change in the stability properties of a fixed point is known as the Hopf bifurcation. The following theorem works for fixed points with one pair of conjugate nonzero purely imaginaryeigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
s. It tells the conditions under which this bifurcation phenomenon occurs.
Theorem (see section 11.2 of ). Let be the Jacobian
In mathematics, a Jacobian, named for Carl Gustav Jacob Jacobi, may refer to:
*Jacobian matrix and determinant
*Jacobian elliptic functions
*Jacobian variety
*Intermediate Jacobian
In mathematics, the intermediate Jacobian of a compact Kähler m ...
of a continuous parametric dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a ...
evaluated at a steady point . Suppose that all eigenvalues of have negative real part except one conjugate nonzero purely imaginary pair . A ''Hopf bifurcation'' arises when these two eigenvalues cross the imaginary axis because of a variation of the system parameters.
Routh–Hurwitz criterion
Routh–Hurwitz criterion (section I.13 of ) gives necessary conditions so that a Hopf bifurcation occurs. Let us see how one can use concretely this idea.Sturm series
Let be Sturm series associated to acharacteristic polynomial
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The chara ...
. They can be written in the form:
:
The coefficients for in correspond to what is called Hurwitz determinants In mathematics, Hurwitz determinants were introduced by , who used them to give a criterion for all roots of a polynomial to have negative real part.
Definition
Consider a characteristic polynomial ''P'' in the variable ''λ'' of the form: ...
. Their definition is related to the associated Hurwitz matrix.
Propositions
Proposition 1. If all the Hurwitz determinants are positive, apart perhaps then the associated Jacobian has no pure imaginary eigenvalues. Proposition 2. If all Hurwitz determinants (for all in are positive, and then all the eigenvalues of the associated Jacobian have negative real parts except a purely imaginary conjugate pair. The conditions that we are looking for so that a Hopf bifurcation occurs (see theorem above) for a parametric continuous dynamical system are given by this last proposition.Example
Consider the classical Van der Pol oscillator written with ordinary differential equations: : The Jacobian matrix associated to this system follows: : The characteristic polynomial (in ) of the linearization at (0,0) is equal to: : The coefficients are:The associated Sturm series is: : The Sturm polynomials can be written as (here ): : The above proposition 2 tells that one must have: : Because 1 > 0 and −1 < 0 are obvious, one can conclude that a Hopf bifurcation may occur for Van der Pol oscillator if .
See also
* Reaction–diffusion systemsReferences
Further reading
* * * * *External links
{{commons category, Hopf bifurcationsThe Hopf Bifurcation
Andronov–Hopf bifurcation page
at
Scholarpedia
''Scholarpedia'' is an English-language wiki-based online encyclopedia with features commonly associated with open-access online academic journals, which aims to have quality content in science and medicine.
''Scholarpedia'' articles are written ...
Bifurcation theory
Circuit theorems