|
5-limit
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as . Powers of 2 represent intervallic movements by octaves. Powers of 3 represent movements by intervals of perfect fifths (plus one octave, which can be removed by multiplying by 1/2, i.e., 2−1). Powers of 5 represent intervals of major thirds (plus two octaves, removable by multiplying by 1/4, i.e., 2−2). Thus, 5-limit tunings are constructed entirely from stacking of three basic purely-tuned intervals (octaves, thirds and fifths). Since the perception of consonance seems related to low numbers in the harmonic series, and 5-limit tuning relies on the three lowest primes, 5-limit tuning should be capable of producing very consona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) (around 21.51 cents). Two notes that differ by this interval would sound different from each other even to untrained ears, , ''BBC''. but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Second
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C; the interval between them is a semitone. In a 12-note approximately equally divided scale, any interval can be defined in terms of an appropriate number of semitones (e.g. a whole tone or major second is 2 semitones wide, a major third 4 semitones, and a perfect fifth 7 semitones. In music theory, a distinction is made between a diatonic semitone, or minor second (an interval encompassing two different staff positions, e.g. from C to D) and a chromatic semitone or augmented unison (an interval between two notes at the same staff position, e.g. from C to C). These are enharmonically equivalent when twelve-tone equal temperament is used, but are not the same thing in meantone te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Intonation
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios (such as 3:2 or 4:3) of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and chords created by combining them) consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth. In Western musical practice, instruments are rarely tuned using only pure intervals—the desire for different keys to have identical intervals in Western music makes this impractical. Some instruments of fixed pitch, such as electric pianos, are commonly tuned using equal temperament, in which all intervals other than octaves consist of irrational-number freque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diminished Triad
In music theory, a diminished triad (also known as the minor flatted fifth) is a triad consisting of two minor thirds above the root. It is a minor triad with a lowered ( flattened) fifth. When using chord symbols, it may be indicated by the symbols "dim", "", "m5", or "MI(5)". However, in most popular-music chord books, the symbol "dim" and "" represents a diminished seventh chord (a four-tone chord), which in some modern jazz books and music theory books is represented by the "dim7" or "7" symbols. For example, the diminished triad built on C, written as C, has pitches C–E–G: : The chord can be represented by the integer notation . In the common practice period, the diminished triad is considered dissonant because of the diminished fifth (or tritone). Harmonic function In major scales, a diminished triad occurs only on the seventh scale degree. For instance, in the key of C, this is a B diminished triad (B, D, F). Since the triad is built on the seventh sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
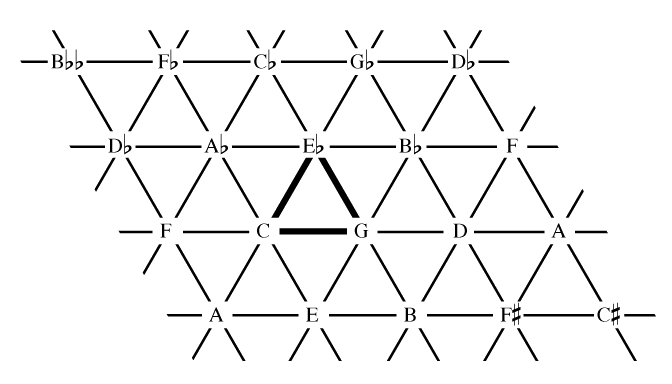
Lattice (music)
In musical tuning, a lattice "is a way of modeling the tuning relationships of a just intonation system. It is an array of points in a periodic multidimensional pattern. Each point on the lattice corresponds to a ratio (i.e., a pitch, or an interval with respect to some other point on the lattice). The lattice can be two-, three-, or ''n''-dimensional, with each dimension corresponding to a different prime-number partial ."Gilmore, Bob (2006). "Introduction", p.xviii, ''"Maximum Clarity" and Other Writings on Music'', edited by Bob Gilmore. Urbana: University of Illinois Press. . When listed in a spreadsheet a lattice may be referred to as a tuning table. The points in a lattice represent pitch classes (or pitches if octaves are represented), and the connectors in a lattice represent the intervals between them. The connecting lines in a lattice display intervals as vectors, so that a line of the same length and angle always has the same intervalic relationship between the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemy's Intense Diatonic Scale
Ptolemy's intense diatonic scale, also known as the Ptolemaic sequence, justly tuned major scale, Ptolemy's tense diatonic scale, or the syntonous (or syntonic) diatonic scale, is a tuning for the diatonic scale proposed by Ptolemy, and corresponding with modern 5-limit just intonation.Chisholm, Hugh (1911). The Encyclopædia Britannica', Vol.28, p. 961. The Encyclopædia Britannica Company. This tuning was declared by Zarlino to be the only tuning that could be reasonably sung, it was also supported by Giuseppe Tartini, and is equivalent to Indian Gandhar tuning which features exactly the same intervals. It is produced through a tetrachord consisting of a greater tone (9:8), lesser tone (10:9), and just diatonic semitone (16:15). This is called Ptolemy's intense diatonic tetrachord (or "tense"), as opposed to Ptolemy's soft diatonic tetrachord (or "relaxed"), which is formed by 21:20, 10:9 and 8:7 intervals. Structure The structure of the intense diatonic scale is shown in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a melodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth (for example C to G) is 3:2 (), 1.5, and may be approximated by an equal tempered perfect fifth () which is 27/12 (about 1.498). If the A above middle C is 440 Hz, the perfect fifth above it would be E, at (440*1.5=) 660 Hz, while the equal tempered E5 is 659.255 Hz. Ratios, rather than direct frequency measurements, allow musicians to work with relative pitch measurements applicable to many instruments in an intuitive manner, whereas one rarely has the frequencies of fixed pitched instruments memorized and rarely has the capabilities to measure the changes of adjustable pitch instruments ( electronic tuner). Ratios have an inverse relationship to string length, for example stopping a string at two-thirds (2:3) its length produces a pitch one and one-half (3:2) that of the open string (not to be confused with inversion). Intervals may be ranke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiditone
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two commonly occurring thirds. It is called ''minor'' because it is the smaller of the two: the major third spans an additional semitone. For example, the interval from A to C is a minor third, as the note C lies three semitones above A. Coincidentally, there are three staff positions from A to C. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones (two and five). The minor third is a skip melodically. Notable examples of ascending minor thirds include the opening two notes of "Greensleeves" and of "Light My Fire". The minor third may be derived from the harmonic series as the interval between the fifth and sixth harmonics, or from the 19th harmonic. The minor third is common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term ''limit'' was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name. The harmonic series and the evolution of music Harry Partch, Ivor Darreg, and Ralph David Hill are among the many microtonalists to suggest that music has been slowly evolving to employ higher and higher harmonics in its constructs (see emancipation of the dissonance). In medieval music, only chords made of octaves and perfect fifths (involving relationships among the first three harmonics) were considered consonant. In the West, triadic harmony arose ( contenance angloise) around the time of the Renaissance, and triads quickly became the fundamental building blocks of Western music. The major and minor thirds of these triads invoke relationships among the first five h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)