|
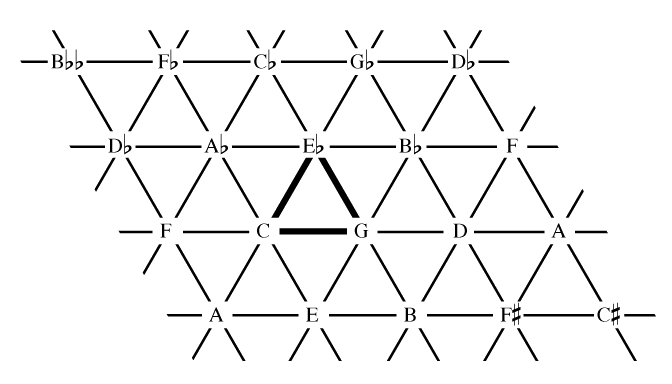
Lattice (music)
In musical tuning, a lattice "is a way of modeling the tuning relationships of a just intonation system. It is an array of points in a periodic multidimensional pattern. Each point on the lattice corresponds to a ratio (i.e., a pitch, or an interval with respect to some other point on the lattice). The lattice can be two-, three-, or ''n''-dimensional, with each dimension corresponding to a different prime-number partial ."Gilmore, Bob (2006). "Introduction", p.xviii, ''"Maximum Clarity" and Other Writings on Music'', edited by Bob Gilmore. Urbana: University of Illinois Press. . When listed in a spreadsheet a lattice may be referred to as a tuning table. The points in a lattice represent pitch classes (or pitches if octaves are represented), and the connectors in a lattice represent the intervals between them. The connecting lines in a lattice display intervals as vectors, so that a line of the same length and angle always has the same intervalic relationship between the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tonnetz
In musical tuning and harmony, the (German for 'tone network') is a conceptual lattice diagram representing tonal space first described by Leonhard Euler in 1739. Various visual representations of the ''Tonnetz'' can be used to show traditional harmonic relationships in European classical music. History through 1900 The ''Tonnetz'' originally appeared in Leonhard Euler's 1739 . Euler's ''Tonnetz'', pictured at left, shows the triadic relationships of the perfect fifth and the major third: at the top of the image is the note F, and to the left underneath is C (a perfect fifth above F), and to the right is A (a major third above F). The ''Tonnetz'' was rediscovered in 1858 by Ernst Naumann, and was disseminated in an 1866 treatise of Arthur von Oettingen. Oettingen and the influential musicologist Hugo Riemann (not to be confused with the mathematician Bernhard Riemann) explored the capacity of the space to chart harmonic motion between chords and modulation between key ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erv Wilson
Ervin Wilson (June 11, 1928 – December 8, 2016) was a Mexican/American (dual citizen) music theorist. Early life Ervin Wilson was born in a remote area of northwest Chihuahua, Mexico, where he lived until the age of fifteen. His mother taught him to play the reed organ and to read musical notation. He began to compose at an early age, but immediately discovered that some of the sounds he was hearing mentally could not be reproduced by the conventional intervals of the organ. As a teenager he began to read books on Indian music, developing an interest in concepts of raga. While he was in the Air Force in Japan, a chance meeting with a total stranger introduced him to musical harmonics, which changed the course of his life and work. Influenced by the work of Joseph Yasser, Wilson began to think of the musical scale as a living process—like a crystal or plant. He mentored many composers and instrument builders. Works Despite his avoidance of academia, Wilson has been influenti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
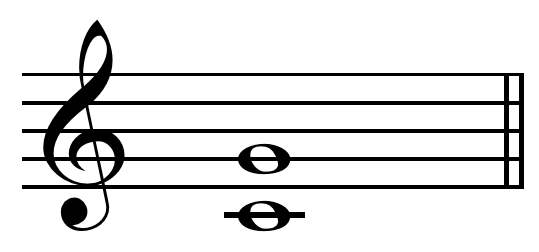
Perfect Fifth
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five consecutive notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant note is a perfect fifth above the tonic note. The perfect fifth is more consonant, or stable, than any other interval except the unison and the octave. It occurs above the root of all major and minor chords (triads) and their extensions. Until the late 19th century, it was often referred to by one of its Gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unison
In music, unison is two or more musical parts that sound either the same pitch or pitches separated by intervals of one or more octaves, usually at the same time. ''Rhythmic unison'' is another term for homorhythm. Definition Unison or perfect unison (also called a prime, or perfect prime)Benward & Saker (2003), p. 53. may refer to the (pseudo-) interval formed by a tone and its duplication (in German, ''Unisono'', ''Einklang'', or ''Prime''), for example C–C, as differentiated from the second, C–D, etc. In the unison the two pitches have the ratio of 1:1 or 0 half steps and zero cents. Although two tones in unison are considered to be the same pitch, they are still perceivable as coming from separate sources, whether played on instruments of a different type: ; or of the same type: . This is because a pair of tones in unison come from different locations or can have different "colors" (timbres), i.e. come from different musical instruments or human voices. Voices w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fourth
A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth () is the fourth spanning five semitones (half steps, or half tones). For example, the ascending interval from C to the next F is a perfect fourth, because the note F is the fifth semitone above C, and there are four staff positions between C and F. Diminished and augmented fourths span the same number of staff positions, but consist of a different number of semitones (four and six, respectively). The perfect fourth may be derived from the harmonic series as the interval between the third and fourth harmonics. The term ''perfect'' identifies this interval as belonging to the group of perfect intervals, so called because they are neither major nor minor. A perfect fourth in just intonation corresponds to a pitch ratio of 4:3, or about 498 cents (), while in equal temperament a perfect fourth is equal to five semitones, or 500 cents (see additive synth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tritone
In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones (six semitones). For instance, the interval from F up to the B above it (in short, F–B) is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B. Narrowly defined, each of these whole tones must be a step in the scale, so by this definition, within a diatonic scale there is only one tritone for each octave. For instance, the above-mentioned interval F–B is the only tritone formed from the notes of the C major scale. More broadly, a tritone is also commonly defined as any interval with a width of three whole tones (spanning six semitones in the chromatic scale), regardless of scale degrees. According to this definition, a diatonic scale contains two tritones for each octave. For instance, the above-mentioned C major scale contains the tritones F–B (from F to the B above it, also called augmented fourth) and B–F (from B to the F above ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Seventh
In music from Western culture, a seventh is a musical interval encompassing seven staff positions (see Interval number for more details), and the major seventh is one of two commonly occurring sevenths. It is qualified as ''major'' because it is the larger of the two. The major seventh spans eleven semitones, its smaller counterpart being the minor seventh, spanning ten semitones. For example, the interval from C to B is a major seventh, as the note B lies eleven semitones above C, and there are seven staff positions from C to B. Diminished and augmented sevenths span the same number of staff positions, but consist of a different number of semitones (nine and twelve). The easiest way to locate and identify the major seventh is from the octave rather than the unison, and it is suggested that one sings the octave first.Keith Wyatt, Carl Schroeder, Joe Elliott (2005). ''Ear Training for the Contemporary Musician'', p.69. . For example, the most commonly cited example of a melody ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and Practice'', p.8. Holt, Rinehart, and Winston. Third edition . "A large 3rd, or ''major 3rd'' (M3) encompassing four half steps." Along with the minor third, the major third is one of two commonly occurring thirds. It is qualified as ''major'' because it is the larger of the two: the major third spans four semitones, the minor third three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones (two and five). The major third may be derived from the harmonic series as the interval between the fourth and fifth harmonics. The maj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Sixth
In music from Western culture, a sixth is a musical interval encompassing six note letter names or staff positions (see Interval number for more details), and the major sixth is one of two commonly occurring sixths. It is qualified as ''major'' because it is the larger of the two. The major sixth spans nine semitones. Its smaller counterpart, the minor sixth, spans eight semitones. For example, the interval from C up to the nearest A is a major sixth. It is a sixth because it encompasses six note letter names (C, D, E, F, G, A) and six staff positions. It is a major sixth, not a minor sixth, because the note A lies nine semitones above C. Diminished and augmented sixths (such as C to A and C to A) span the same number of note letter names and staff positions, but consist of a different number of semitones (seven and ten, respectively). A commonly cited example of a melody featuring the major sixth as its opening is " My Bonnie Lies Over the Ocean".Blake Neely, ''Piano For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of Fifths
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths. (This is strictly true in the standard 12-tone equal temperament system — using a different system requires one interval of diminished sixth to be treated as a fifth). If C is chosen as a starting point, the sequence is: C, G, D, A, E, B (=C), F (=G), C (=D), A, E, B, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle. Definition The circle of fifths organizes pitches in a sequence of perfect fifths, generally shown as a circle with the pitches (and their corresponding keys) in a clockwise progression. Musicians and composers often use the circle of fifths to describe the musical relationships between pitches. Its design is helpful in composing and harmonizing melodies, building chords, and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime-counting Function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number ''x''. It is denoted by (''x'') (unrelated to the number ). History Of great interest in number theory is the growth rate of the prime-counting function. It was conjectured in the end of the 18th century by Gauss and by Legendre to be approximately : \frac x where log is the natural logarithm, in the sense that :\lim_ \frac=1. This statement is the prime number theorem. An equivalent statement is :\lim_\pi(x) / \operatorname(x)=1 where li is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard and by Charles de la Vallée Poussin independently, using properties of the Riemann zeta function introduced by Riemann in 1859. Proofs of the prime number theorem not using the zeta function or complex analysis were found around 1948 by Atle Selberg and by Paul Erdős (for the most ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave Equivalence
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music," the use of which is "common in most musical systems." The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' ( it, all'ottava), ''8va bassa'' ( it, all'ottava bassa, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |