|
Arrow–Debreu Model
In mathematical economics, the Arrow–Debreu model is a theoretical general equilibrium model. It posits that under certain economic assumptions (convex preferences, perfect competition, and demand independence), there must be a set of prices such that Aggregate supply, aggregate supplies will equal aggregate demands for every commodity in the economy. The model is central to the theory of General equilibrium, general (economic) equilibrium, and it is used as a general reference for other microeconomic models. It was proposed by Kenneth Arrow, Gérard Debreu in 1954, and Lionel W. McKenzie independently in 1954, with later improvements in 1959. The A-D model is one of the most general models of competitive economy and is a crucial part of general equilibrium theory, as it can be used to prove the existence of general equilibrium (or Walrasian equilibrium) of an economy. In general, there may be many equilibria. Arrow (1972) and Debreu (1983) were separately awarded the Nobel Me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Economics
Mathematical economics is the application of Mathematics, mathematical methods to represent theories and analyze problems in economics. Often, these Applied mathematics#Economics, applied methods are beyond simple geometry, and may include differential and integral calculus, Recurrence relation, difference and differential equations, Matrix (mathematics), matrix algebra, mathematical programming, or other Computational economics, computational methods.TOC. Proponents of this approach claim that it allows the formulation of theoretical relationships with rigor, generality, and simplicity. Mathematics allows economists to form meaningful, testable propositions about wide-ranging and complex subjects which could less easily be expressed informally. Further, the language of mathematics allows economists to make specific, positiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Market Clearing
In economics, market clearing is the process by which, in an economic market, the supply of whatever is traded is equated to the demand so that there is no excess supply or demand, ensuring that there is neither a surplus nor a shortage. The new classical economics assumes that in any given market, assuming that all buyers and sellers have access to information and that there is no "friction" impeding price changes, prices ''constantly'' adjust up or down to ensure market clearing. Mechanism and examples A market-clearing price is the price of a good or service at which the quantity supplied equals the quantity demanded, also called the equilibrium price. The theory claims that markets tend to move toward this price. Supply is fixed for a one-time sale of goods, so the market-clearing price is simply the maximum price at which all items can be sold. In a market where goods are produced and sold on an ongoing basis, the theory predicts that the market will move toward a price wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kakutani Fixed-point Theorem
In mathematical analysis, the Kakutani fixed-point theorem is a fixed-point theorem for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex, compact subset of a Euclidean space to have a fixed point, i.e. a point which is mapped to a set containing it. The Kakutani fixed point theorem is a generalization of the Brouwer fixed point theorem. The Brouwer fixed point theorem is a fundamental result in topology which proves the existence of fixed points for continuous functions defined on compact, convex subsets of Euclidean spaces. Kakutani's theorem extends this to set-valued functions. The theorem was developed by Shizuo Kakutani in 1941, and was used by John Nash in his description of Nash equilibria. It has subsequently found widespread application in game theory and economics. Statement Kakutani's theorem states: : ''Let'' ''S'' ''be a non-empty, compact and convex subset of some Euclidean space'' R''n''. :''Let'' ''φ'':&n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lionel McKenzie
Lionel Wilfred McKenzie (January 26, 1919 – October 12, 2010) was an American economist. He was the Wilson Professor Emeritus of Economics at the University of Rochester. He was born in Montezuma, Georgia. He completed undergraduate studies at Duke University in 1939 and subsequently moved to Oxford that year as a Rhodes Scholar. McKenzie worked with the Cowles Commission while it was in Chicago and served as an assistant professor at Duke from 1948 to 1957. Having received his Ph.D. at Princeton University in 1956, McKenzie moved to Rochester where he was responsible for the establishment of the graduate program in economics. McKenzie has been the recipient of numerous professional awards, including the Guggenheim Fellowship in 1973, election to the United States National Academy of Sciences in 1978, the Order of the Rising Sun in 1995 and honorary doctorates from Keio University in 1998 and Kyoto University in 2004. The latter three reflect the success of his many Japanese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of "dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contraction Mapping
In mathematics, a contraction mapping, or contraction or contractor, on a metric space (''M'', ''d'') is a function ''f'' from ''M'' to itself, with the property that there is some real number 0 \leq k < 1 such that for all ''x'' and ''y'' in ''M'', : The smallest such value of ''k'' is called the Lipschitz constant of ''f''. Contractive maps are sometimes called Lipschitzian maps. If the above condition is instead satisfied for ''k'' ≤ 1, then the mapping is said to be a non-expansive map. More generally, the idea of a contractive mapping can be defined for maps between metric spaces. Thus, if (''M'', ''d'') and (''N'', ''d) are two metric spaces, then is a contractive mapping if there is a constant such that : |
Interior Solution (optimization)
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Optimization problems can be divided into two categories, depending on whether the variables ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
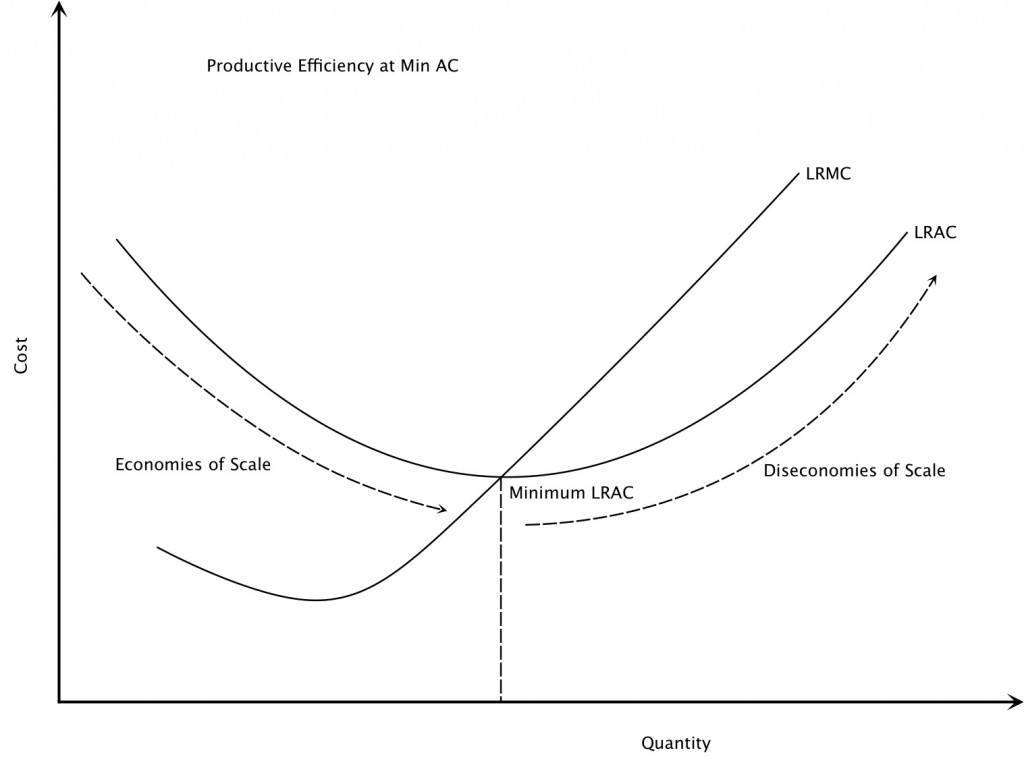
Economies Of Scale
In microeconomics, economies of scale are the cost advantages that enterprises obtain due to their scale of operation, and are typically measured by the amount of Productivity, output produced per unit of cost (production cost). A decrease in unit cost, cost per unit of output enables an increase in scale that is, increased production with lowered cost. At the basis of economies of scale, there may be technical, statistical, organizational or related factors to the degree of Market (economics), market control. Economies of scale arise in a variety of organizational and business situations and at various levels, such as a production, plant or an entire enterprise. When average costs start falling as output increases, then economies of scale occur. Some economies of scale, such as capital cost of manufacturing facilities and friction loss of transportation and industrial equipment, have a physical or engineering basis. The economic concept dates back to Adam Smith and the idea o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diseconomies Of Scale
In microeconomics, diseconomies of scale are the cost disadvantages that economic actors accrue due to an increase in organizational size or in output, resulting in production of Product (business), goods and Service (economics), services at increased average cost, per-unit costs. The concept of diseconomies of scale is the opposite of economies of scale. It occurs when economies of scale become dysfunctional for a firm. In business, diseconomies of scale are the features that lead to an increase in average costs as a business grows beyond a certain size. Causes Communication costs Ideally, all employees of a firm would have one-on-one communication with each other so they know exactly what the other workers are doing. A firm with a single worker does not require any communication between employees. A firm with two workers requires one communication channel, directly between those two workers. A firm with three workers requires three communication channels between employees (betwee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shapley–Folkman Lemma
The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of set (mathematics), sets in a vector space. The lemma may be intuitively understood as saying that, if the number of summed sets exceeds the dimension (linear algebra), dimension of the vector space, then their Minkowski sum is approximately convex. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross Starr, Ross M. Starr. Related results provide more refined statements about how close the approximation is. For example, the Shapley–Folkman theorem provides an upper bound on the Euclidean distance, distance between any point in the Minkowski sum and its convex hull. This upper bound is sharpened by the Shapley–Folkman–Starr theorem (alternatively, Starr's corollary). The Shapley–Folkman lemma has applications in economics, mathematical optimization, optimization and probability theory. In economics, it can be use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diminishing Marginal Utility
Marginal utility, in mainstream economics, describes the change in ''utility'' (pleasure or satisfaction resulting from the consumption) of one unit of a good or service. Marginal utility can be positive, negative, or zero. Negative marginal utility implies that every consumed additional unit of a commodity causes more harm than good, leading to a decrease in overall utility. In contrast, positive marginal utility indicates that every additional unit consumed increases overall utility. In the context of cardinal utility, liberal economists postulate a law of diminishing marginal utility. This law states that the first unit of consumption of a good or service yields more satisfaction or utility than the subsequent units, and there is a continuing reduction in satisfaction or utility for greater amounts. As consumption increases, the additional satisfaction or utility gained from each additional unit consumed falls, a concept known as ''diminishing marginal utility.'' This idea is u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |