Angular momentum (sometimes called moment of momentum or rotational momentum) is the
rotational analog of
linear momentum. It is an important
physical quantity
A physical quantity (or simply quantity) is a property of a material or system that can be Quantification (science), quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a ''nu ...
because it is a
conserved quantity – the total angular momentum of a
closed system remains constant. Angular momentum has both a
direction and a magnitude, and both are conserved.
Bicycles and motorcycles,
flying discs,
rifled bullets, and
gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why
hurricane
A tropical cyclone is a rapidly rotating storm system with a low-pressure area, a closed low-level atmospheric circulation, strong winds, and a spiral arrangement of thunderstorms that produce heavy rain and squalls. Depending on its ...
s
form spirals and
neutron star
A neutron star is the gravitationally collapsed Stellar core, core of a massive supergiant star. It results from the supernova explosion of a stellar evolution#Massive star, massive star—combined with gravitational collapse—that compresses ...
s have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it.
The three-dimensional angular momentum for a
point particle is classically represented as a
pseudovector , the
cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
of the particle's
position vector (relative to some origin) and its
momentum vector; the latter is in
Newtonian mechanics. Unlike linear momentum, angular momentum depends on where this origin is chosen, since the particle's position is measured from it.
Angular momentum is an
extensive quantity; that is, the total angular momentum of any composite system is the sum of the angular momenta of its constituent parts. For a
continuous rigid body or a
fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
, the total angular momentum is the
volume integral of angular momentum density (angular momentum per unit volume in the limit as volume shrinks to zero) over the entire body.
Similar to conservation of linear momentum, where it is conserved if there is no external force, angular momentum is conserved if there is no external
torque. Torque can be defined as the rate of change of angular momentum, analogous to
force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
. The net ''external'' torque on any system is always equal to the ''total'' torque on the system; the sum of all internal torques of any system is always 0 (this is the rotational analogue of
Newton's third law of motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body r ...
). Therefore, for a
closed system (where there is no net external torque), the ''total'' torque on the system must be 0, which means that the total angular momentum of the system is constant.
The change in angular momentum for a particular interaction is called angular impulse, sometimes twirl. Angular impulse is the angular analog of (linear)
impulse.
Examples
The trivial case of the angular momentum
of a body in an orbit is given by
where
is the
mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
of the orbiting object,
is the orbit's
frequency and
is the orbit's radius.
The angular momentum
of a uniform rigid sphere rotating around its axis, instead, is given by
where
is the sphere's mass,
is the frequency of rotation and
is the sphere's radius.
Thus, for example, the orbital angular momentum of the
Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
with respect to the Sun is about 2.66 × 10
40 kg⋅m
2⋅s
−1, while its rotational angular momentum is about 7.05 × 10
33 kg⋅m
2⋅s
−1.
In the case of a uniform rigid sphere rotating around its axis, if, instead of its mass, its
density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
is known, the angular momentum
is given by
where
is the sphere's
density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
,
is the frequency of rotation and
is the sphere's radius.
In the simplest case of a spinning disk, the angular momentum
is given by
[
]
where
is the disk's mass,
is the frequency of rotation and
is the disk's radius.
If instead the disk rotates about its diameter (e.g. coin toss), its angular momentum
is given by
Definition in classical mechanics
Just as for
angular velocity, there are two special types of angular
momentum of an object: the spin angular momentum is the angular momentum about the object's
center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
, while the orbital angular momentum is the angular momentum about a chosen center of rotation. The
Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
has an orbital angular momentum by nature of revolving around the
Sun, and a spin angular momentum by nature of its daily rotation around the polar axis. The total angular momentum is the sum of the spin and orbital angular momenta. In the case of the Earth the primary conserved quantity is the total angular momentum of the
Solar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Sola ...
because angular momentum is exchanged to a small but important extent among the planets and the Sun. The orbital angular momentum vector of a point particle is always parallel and directly proportional to its orbital angular
velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
vector ω, where the constant of proportionality depends on both the mass of the particle and its distance from origin. The spin angular momentum vector of a rigid body is proportional but not always parallel to the spin angular velocity vector Ω, making the constant of proportionality a second-rank
tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
rather than a scalar.
Orbital angular momentum in two dimensions

Angular momentum is a
vector quantity (more precisely, a
pseudovector) that represents the product of a body's
rotational inertia and
rotational velocity (in radians/sec) about a particular axis. However, if the particle's trajectory lies in a single
plane, it is sufficient to discard the vector nature of angular momentum, and treat it as a
scalar (more precisely, a
pseudoscalar).
[
] Angular momentum can be considered a rotational analog of linear momentum. Thus, where linear momentum is proportional to
mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
and
linear speed
angular momentum is proportional to
moment of inertia and
angular speed measured in radians per second.
Unlike mass, which depends only on amount of matter, moment of inertia depends also on the position of the axis of rotation and the distribution of the matter. Unlike linear velocity, which does not depend upon the choice of origin, orbital angular velocity is always measured with respect to a fixed origin. Therefore, strictly speaking, should be referred to as the angular momentum ''relative to that center''.
[
]
In the case of circular motion of a single particle, we can use
and
to expand angular momentum as
reducing to:
the product of the
radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...
of rotation and the linear momentum of the particle
, where
is the
linear (tangential) speed.
This simple analysis can also apply to non-circular motion if one uses the component of the motion
perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
to the
radius vector:
where
is the perpendicular component of the motion. Expanding,
rearranging,
and reducing, angular momentum can also be expressed,
where
is the length of the
''moment arm'', a line dropped perpendicularly from the origin onto the path of the particle. It is this definition, , to which the term ''moment of momentum'' refers.
Scalar angular momentum from Lagrangian mechanics
Another approach is to define angular momentum as the conjugate momentum (also called canonical momentum) of the angular coordinate
expressed in the
Lagrangian of the mechanical system. Consider a mechanical system with a mass
constrained to move in a circle of radius
in the absence of any external force field. The kinetic energy of the system is
And the potential energy is
Then the Lagrangian is
The ''generalized momentum'' "canonically conjugate to" the coordinate
is defined by
Orbital angular momentum in three dimensions
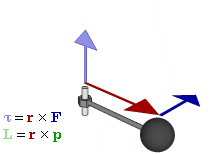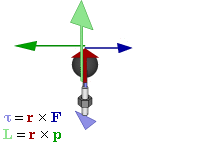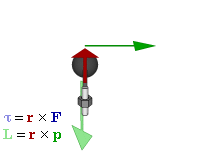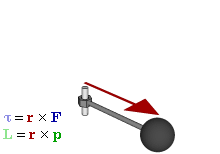
To completely define orbital angular momentum in
three dimensions, it is required to know the rate at which the position vector sweeps out an angle, the direction perpendicular to the instantaneous plane of
angular displacement, and the
mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
involved, as well as how this mass is distributed in space. By retaining this
vector nature of angular momentum, the general nature of the equations is also retained, and can describe any sort of three-dimensional
motion
In physics, motion is when an object changes its position with respect to a reference point in a given time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed, and frame of reference to an o ...
about the center of rotation –
circular,
linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
, or otherwise. In
vector notation, the orbital angular momentum of a
point particle in motion about the origin can be expressed as:
where
*
is the
moment of inertia for a
point mass,
*
is the orbital
angular velocity of the particle about the origin,
*
is the position vector of the particle relative to the origin, and
,
*
is the linear velocity of the particle relative to the origin, and
*
is the mass of the particle.
This can be expanded, reduced, and by the rules of
vector algebra, rearranged:
which is the
cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
of the position vector
and the linear momentum
of the particle. By the definition of the cross product, the
vector is
perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
to both
and
. It is directed perpendicular to the plane of angular displacement, as indicated by the
right-hand rule – so that the angular velocity is seen as
counter-clockwise from the head of the vector. Conversely, the
vector defines the
plane in which
and
lie.
By defining a
unit vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ...
perpendicular to the plane of angular displacement, a
scalar angular speed results, where
and
where
is the perpendicular component of the motion, as above.
The two-dimensional scalar equations of the previous section can thus be given direction:
and
for circular motion, where all of the motion is perpendicular to the radius
.
In the
spherical coordinate system the angular momentum vector expresses as
:
Analogy to linear momentum
Angular momentum can be described as the rotational analog of
linear momentum. Like linear momentum it involves elements of
mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
and
displacement. Unlike linear momentum it also involves elements of
position and
shape
A shape is a graphics, graphical representation of an object's form or its external boundary, outline, or external Surface (mathematics), surface. It is distinct from other object properties, such as color, Surface texture, texture, or material ...
.
Many problems in physics involve matter in motion about some certain point in space, be it in actual rotation about it, or simply moving past it, where it is desired to know what effect the moving matter has on the point—can it exert energy upon it or perform work about it?
Energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
, the ability to do
work, can be stored in matter by setting it in motion—a combination of its
inertia and its displacement. Inertia is measured by its
mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
, and displacement by its
velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
. Their product,
is the matter's
momentum. Referring this momentum to a central point introduces a complication: the momentum is not applied to the point directly. For instance, a particle of matter at the outer edge of a wheel is, in effect, at the end of a
lever
A lever is a simple machine consisting of a beam (structure), beam or rigid rod pivoted at a fixed hinge, or '':wikt:fulcrum, fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, l ...
of the same length as the wheel's radius, its momentum turning the lever about the center point. This imaginary lever is known as the ''moment arm''. It has the effect of multiplying the momentum's effort in proportion to its length, an effect known as a
''moment''. Hence, the particle's momentum referred to a particular point,
is the ''angular momentum'', sometimes called, as here, the ''moment of momentum'' of the particle versus that particular center point. The equation
combines a moment (a mass
turning moment arm
) with a linear (straight-line equivalent) speed
. Linear speed referred to the central point is simply the product of the distance
and the angular speed
versus the point:
another moment. Hence, angular momentum contains a double moment:
Simplifying slightly,
the quantity
is the particle's
moment of inertia, sometimes called the second moment of mass. It is a measure of rotational inertia.
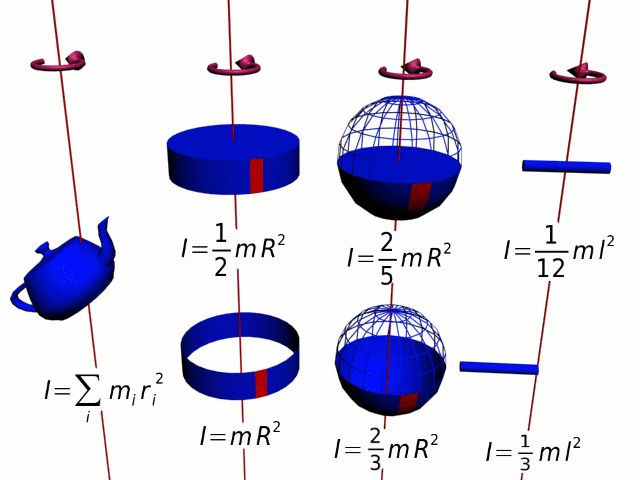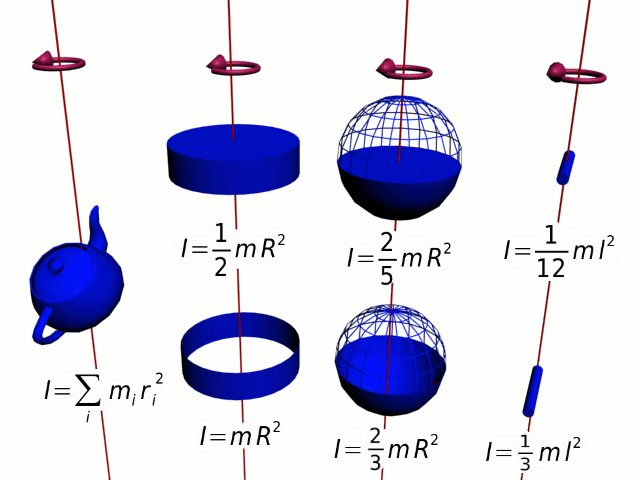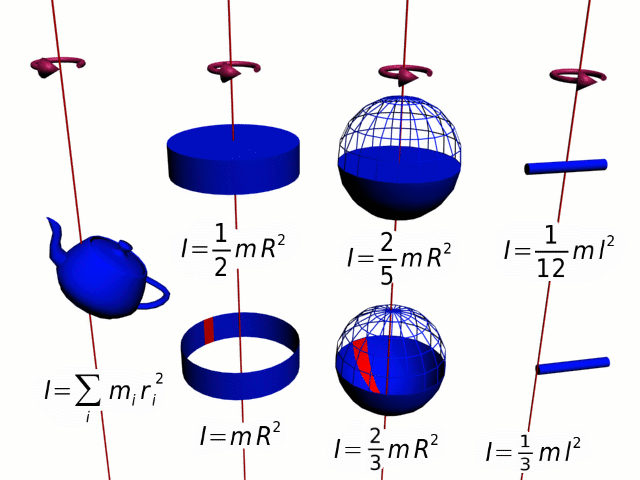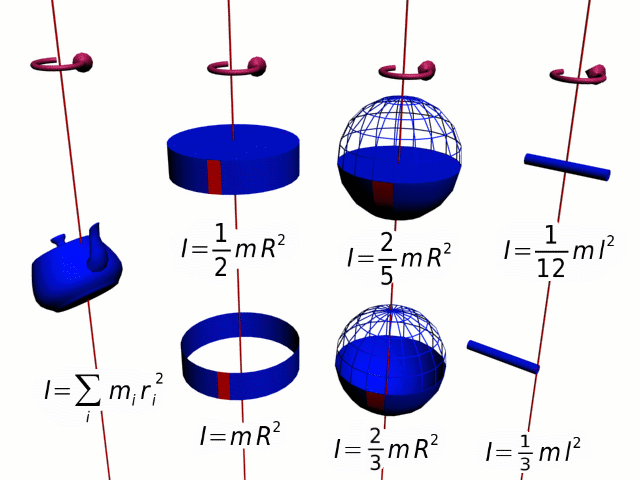
The above analogy of the translational momentum and rotational momentum can be expressed in vector form:
*
for linear motion
*
for rotation
The direction of momentum is related to the direction of the velocity for linear movement. The direction of angular momentum is related to the angular velocity of the rotation.
Because
moment of inertia is a crucial part of the spin angular momentum, the latter necessarily includes all of the complications of the former, which is calculated by multiplying elementary bits of the mass by the
squares
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
of their
distances from the center of rotation.
[
] Therefore, the total moment of inertia, and
the angular momentum, is a complex function of the configuration of the
matter
In classical physics and general chemistry, matter is any substance that has mass and takes up space by having volume. All everyday objects that can be touched are ultimately composed of atoms, which are made up of interacting subatomic pa ...
about the center of rotation and the orientation of the rotation for the various bits.
For a
rigid body, for instance a wheel or an asteroid, the orientation of rotation is simply the position of the
rotation axis versus the matter of the body. It may or may not pass through the
center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
, or it may lie completely outside of the body. For the same body, angular momentum may take a different value for every possible axis about which rotation may take place. It reaches a minimum when the axis passes through the center of mass.
For a collection of objects revolving about a center, for instance all of the bodies of the
Solar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Sola ...
, the orientations may be somewhat organized, as is the Solar System, with most of the bodies' axes lying close to the system's axis. Their orientations may also be completely random.
In brief, the more mass and the farther it is from the center of rotation (the longer the
moment arm
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek alphabet, Greek let ...
), the greater the moment of inertia, and therefore the greater the angular momentum for a given
angular velocity. In many cases the
moment of inertia, and hence the angular momentum, can be simplified by,
where
is the
radius of gyration, the distance from the axis at which the entire mass
may be considered as concentrated.
Similarly, for a
point mass the
moment of inertia is defined as,
where
is the
radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...
of the point mass from the center of rotation, and for any collection of particles
as the sum,
Angular momentum's dependence on position and shape is reflected in its
units versus linear momentum: kg⋅m
2/s or N⋅m⋅s for angular momentum versus
kg⋅m/s or
N⋅s for linear momentum. When calculating angular momentum as the product of the moment of inertia times the angular velocity, the angular velocity must be expressed in radians per second, where the radian assumes the dimensionless value of unity. (When performing dimensional analysis, it may be productive to use
orientational analysis which treats radians as a base unit, but this is not done in the
International system of units
The International System of Units, internationally known by the abbreviation SI (from French ), is the modern form of the metric system and the world's most widely used system of measurement. It is the only system of measurement with official s ...
). The units if angular momentum can be interpreted as
torque⋅time. An object with angular momentum of can be reduced to zero angular velocity by an angular
impulse of .
The
plane perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
to the axis of angular momentum and passing through the center of mass is sometimes called the ''invariable plane'', because the direction of the axis remains fixed if only the interactions of the bodies within the system, free from outside influences, are considered.
[
] One such plane is the
invariable plane of the Solar System.
Angular momentum and torque
Newton's second law of motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body re ...
can be expressed mathematically,
or
force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
=
mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
×
acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
. The rotational equivalent for point particles may be derived as follows:
which means that the torque (i.e. the time
derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
of the angular momentum) is
Because the moment of inertia is
, it follows that
, and
which, reduces to
This is the rotational analog of Newton's second law. Note that the torque is not necessarily proportional or parallel to the
angular acceleration (as one might expect). The reason for this is that the moment of inertia of a particle can change with time, something that cannot occur for ordinary mass.
Conservation of angular momentum
General considerations
A rotational analog of
Newton's third law of motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body r ...
might be written, "In a
closed system, no torque can be exerted on any matter without the exertion on some other matter of an equal and opposite torque about the same axis."
Hence, ''angular momentum can be exchanged between objects in a closed system, but total angular momentum before and after an exchange remains constant (is conserved)''.
Seen another way, a rotational analogue of
Newton's first law of motion might be written, "A rigid body continues in a state of uniform rotation unless acted upon by an external influence."
[
] Thus ''with no external influence to act upon it, the original angular momentum of the system remains constant''.
The conservation of angular momentum is used in analyzing
''central force motion''. If the net force on some body is directed always toward some point, the ''center'', then there is no torque on the body with respect to the center, as all of the force is directed along the
radius vector, and none is
perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
to the radius. Mathematically, torque
because in this case
and
are parallel vectors. Therefore, the angular momentum of the body about the center is constant. This is the case with
gravitational attraction in the
orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an ...
s of
planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets b ...
s and
satellite
A satellite or an artificial satellite is an object, typically a spacecraft, placed into orbit around a celestial body. They have a variety of uses, including communication relay, weather forecasting, navigation ( GPS), broadcasting, scient ...
s, where the gravitational force is always directed toward the primary body and orbiting bodies conserve angular momentum by exchanging distance and velocity as they move about the primary. Central force motion is also used in the analysis of the
Bohr model
In atomic physics, the Bohr model or Rutherford–Bohr model was a model of the atom that incorporated some early quantum concepts. Developed from 1911 to 1918 by Niels Bohr and building on Ernest Rutherford's nuclear Rutherford model, model, i ...
of the
atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
.
For a planet, angular momentum is distributed between the spin of the planet and its revolution in its orbit, and these are often exchanged by various mechanisms. The conservation of angular momentum in the
Earth–Moon system results in the transfer of angular momentum from Earth to Moon, due to
tidal torque the Moon exerts on the Earth. This in turn results in the slowing down of the rotation rate of Earth, at about 65.7 nanoseconds per day, and in gradual increase of the radius of Moon's orbit, at about 3.82 centimeters per year.

The conservation of angular momentum explains the angular acceleration of an
ice skater as they bring their arms and legs close to the vertical axis of rotation. By bringing part of the mass of their body closer to the axis, they decrease their body's moment of inertia. Because angular momentum is the product of
moment of inertia and
angular velocity, if the angular momentum remains constant (is conserved), then the angular velocity (rotational speed) of the skater must increase.
The same phenomenon results in extremely fast spin of compact stars (like
white dwarf
A white dwarf is a Compact star, stellar core remnant composed mostly of electron-degenerate matter. A white dwarf is very density, dense: in an Earth sized volume, it packs a mass that is comparable to the Sun. No nuclear fusion takes place i ...
s,
neutron star
A neutron star is the gravitationally collapsed Stellar core, core of a massive supergiant star. It results from the supernova explosion of a stellar evolution#Massive star, massive star—combined with gravitational collapse—that compresses ...
s and
black hole
A black hole is a massive, compact astronomical object so dense that its gravity prevents anything from escaping, even light. Albert Einstein's theory of general relativity predicts that a sufficiently compact mass will form a black hole. Th ...
s) when they are formed out of much larger and slower rotating stars.
Conservation is not always a full explanation for the dynamics of a system but is a key constraint. For example, a
spinning top is subject to gravitational torque making it lean over and change the angular momentum about the
nutation axis, but neglecting friction at the point of spinning contact, it has a conserved angular momentum about its spinning axis, and another about its
precession axis. Also, in any
planetary system, the planets, star(s), comets, and asteroids can all move in numerous complicated ways, but only so that the angular momentum of the system is conserved.
Noether's theorem states that every
conservation law is associated with a
symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
(invariant) of the underlying physics. The symmetry associated with conservation of angular momentum is
rotational invariance. The fact that the physics of a system is unchanged if it is rotated by any angle about an axis implies that angular momentum is conserved.
Relation to Newton's second law of motion
While angular momentum total conservation can be understood separately from
Newton's laws of motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body re ...
as stemming from
Noether's theorem in systems symmetric under rotations, it can also be understood simply as an efficient method of calculation of results that can also be otherwise arrived at directly from Newton's second law, together with laws governing the forces of nature (such as Newton's third law,
Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, Electrical network, electr ...
and
Lorentz force). Indeed, given initial conditions of position and velocity for every point, and the forces at such a condition, one may use Newton's second law to calculate the second derivative of position, and solving for this gives full information on the development of the physical system with time. Note, however, that this is no longer true in
quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, due to the existence of
particle spin, which is an angular momentum that cannot be described by the cumulative effect of point-like motions in space.
As an example, consider decreasing of the
moment of inertia, e.g. when a
figure skater is pulling in their hands, speeding up the circular motion. In terms of angular momentum conservation, we have, for angular momentum ''L'', moment of inertia ''I'' and angular velocity ''ω'':
Using this, we see that the change requires an energy of:
so that a decrease in the moment of inertia requires investing energy.
This can be compared to the work done as calculated using Newton's laws. Each point in the rotating body is accelerating, at each point of time, with radial acceleration of:
Let us observe a point of mass ''m'', whose position vector relative to the center of motion is perpendicular to the z-axis at a given point of time, and is at a distance ''z''. The
centripetal force on this point, keeping the circular motion, is:
Thus the work required for moving this point to a distance ''dz'' farther from the center of motion is:
For a non-pointlike body one must integrate over this, with ''m'' replaced by the mass density per unit ''z''. This gives:
which is exactly the energy required for keeping the angular momentum conserved.
Note, that the above calculation can also be performed per mass, using
kinematics
In physics, kinematics studies the geometrical aspects of motion of physical objects independent of forces that set them in motion. Constrained motion such as linked machine parts are also described as kinematics.
Kinematics is concerned with s ...
only. Thus the phenomena of figure skater accelerating tangential velocity while pulling their hands in, can be understood as follows in layman's language: The skater's palms are not moving in a straight line, so they are constantly accelerating inwards, but do not gain additional speed because the accelerating is always done when their motion inwards is zero. However, this is different when pulling the palms closer to the body: The acceleration due to rotation now increases the speed; but because of the rotation, the increase in speed does not translate to a significant speed inwards, but to an increase of the rotation speed.
Stationary-action principle
In classical mechanics it can be shown that the rotational invariance of action functionals implies conservation of angular momentum. The action is defined in classical physics as a functional of positions,
often represented by the use of square brackets, and the final and initial times. It assumes the following form in cartesian coordinates:
where the repeated indices indicate summation over the index. If the action is invariant of an infinitesimal transformation, it can be mathematically stated as:
.
Under the transformation,
, the action becomes:
where we can employ the expansion of the terms up-to first order in
:
giving the following change in action:
Since all rotations can be expressed as
matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrix, square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exp ...
of skew-symmetric matrices, i.e. as
where
is a skew-symmetric matrix and
is angle of rotation, we can express the change of coordinates due to the rotation
, up-to first order of infinitesimal angle of rotation,
as:
Combining the equation of motion and rotational invariance of action, we get from the above equations that:
Since this is true for any matrix
that satisfies
it results in the conservation of the following quantity:
as
. This corresponds to the conservation of angular momentum throughout the motion.
Lagrangian formalism
In
Lagrangian mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the ...
, angular momentum for rotation around a given axis, is the
conjugate momentum of the
generalized coordinate of the angle around the same axis. For example,
, the angular momentum around the z axis, is:
where
is the Lagrangian and
is the angle around the z axis.
Note that
, the time derivative of the angle, is the
angular velocity . Ordinarily, the Lagrangian depends on the angular velocity through the kinetic energy: The latter can be written by separating the velocity to its radial and tangential part, with the tangential part at the x-y plane, around the z-axis, being equal to:
where the subscript i stands for the i-th body, and ''m'', ''v''
''T'' and ''ω''
''z'' stand for mass, tangential velocity around the z-axis and angular velocity around that axis, respectively.
For a body that is not point-like, with density ''ρ'', we have instead:
where integration runs over the area of the body, and ''I''
z is the moment of inertia around the z-axis.
Thus, assuming the potential energy does not depend on ''ω''
''z'' (this assumption may fail for electromagnetic systems), we have the angular momentum of the ''i''th object:
We have thus far rotated each object by a separate angle; we may also define an overall angle ''θ''
z by which we rotate the whole system, thus rotating also each object around the z-axis, and have the overall angular momentum:
From
Euler–Lagrange equations it then follows that:
Since the lagrangian is dependent upon the angles of the object only through the potential, we have:
which is the torque on the ''i''th object.
Suppose the system is invariant to rotations, so that the potential is independent of an overall rotation by the angle ''θ''
z (thus it may depend on the angles of objects only through their differences, in the form
). We therefore get for the total angular momentum:
And thus the angular momentum around the z-axis is conserved.
This analysis can be repeated separately for each axis, giving conversation of the angular momentum vector. However, the angles around the three axes cannot be treated simultaneously as generalized coordinates, since they are not independent; in particular, two angles per point suffice to determine its position. While it is true that in the case of a rigid body, fully describing it requires, in addition to three
translational degrees of freedom, also specification of three rotational degrees of freedom; however these cannot be defined as rotations around the
Cartesian axes (see
Euler angles). This caveat is reflected in quantum mechanics in the non-trivial
commutation relations of the different components of the
angular momentum operator.
Hamiltonian formalism
Equivalently, in
Hamiltonian mechanics
In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (gener ...
the Hamiltonian can be described as a function of the angular momentum. As before, the part of the kinetic energy related to rotation around the z-axis for the ''i''th object is:
which is analogous to the energy dependence upon momentum along the z-axis,
.
Hamilton's equations relate the angle around the z-axis to its conjugate momentum, the angular momentum around the same axis:
The first equation gives
And so we get the same results as in the Lagrangian formalism.
Note, that for combining all axes together, we write the kinetic energy as:
where ''p''
r is the momentum in the radial direction, and the
moment of inertia is a 3-dimensional matrix; bold letters stand for 3-dimensional vectors.
For point-like bodies we have:
This form of the kinetic energy part of the Hamiltonian is useful in analyzing
central potential problems, and is easily transformed to a
quantum mechanical work frame (e.g. in the
hydrogen atom problem).
Angular momentum in orbital mechanics
While in classical mechanics the language of angular momentum can be replaced by Newton's laws of motion, it is particularly useful for motion in
central potential such as planetary motion in the solar system. Thus, the orbit of a planet in the solar system is defined by its energy, angular momentum and angles of the orbit major axis relative to a coordinate frame.
In astrodynamics and
celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, a quantity closely related to angular momentum is defined as
called ''
specific angular momentum''. Note that
Mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
is often unimportant in orbital mechanics calculations, because motion of a body is determined by
gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
. The primary body of the system is often so much larger than any bodies in motion about it that the gravitational effect of the smaller bodies on it can be neglected; it maintains, in effect, constant velocity. The motion of all bodies is affected by its gravity in the same way, regardless of mass, and therefore all move approximately the same way under the same conditions.
Solid bodies
Angular momentum is also an extremely useful concept for describing rotating rigid bodies such as a
gyroscope or a rocky planet.
For a continuous mass distribution with
density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
function ''ρ''(r), a differential
volume element ''dV'' with
position vector r within the mass has a mass element ''dm'' = ''ρ''(r)''dV''. Therefore, the
infinitesimal angular momentum of this element is:
and
integrating this
differential over the volume of the entire mass gives its total angular momentum:
In the derivation which follows, integrals similar to this can replace the sums for the case of continuous mass.
Collection of particles

For a collection of particles in motion about an arbitrary origin, it is informative to develop the equation of angular momentum by resolving their motion into components about their own center of mass and about the origin. Given,
*
is the mass of particle
,
*
is the position vector of particle
w.r.t. the origin,
*
is the velocity of particle
w.r.t. the origin,
*
is the position vector of the center of mass w.r.t. the origin,
*
is the velocity of the center of mass w.r.t. the origin,
*
is the position vector of particle
w.r.t. the center of mass,
*
is the velocity of particle
w.r.t. the center of mass,
The total mass of the particles is simply their sum,
The position vector of the center of mass is defined by,
By inspection,
:
and
The total angular momentum of the collection of particles is the sum of the angular momentum of each particle,
Expanding
,
:
Expanding
,
:
It can be shown that (see sidebar),
:
and
therefore the second and third terms vanish,
:
The first term can be rearranged,
:
and total angular momentum for the collection of particles is finally,
The first term is the angular momentum of the center of mass relative to the origin. Similar to ', below, it is the angular momentum of one particle of mass ''M'' at the center of mass moving with velocity V. The second term is the angular momentum of the particles moving relative to the center of mass, similar to ', below. The result is general—the motion of the particles is not restricted to rotation or revolution about the origin or center of mass. The particles need not be individual masses, but can be elements of a continuous distribution, such as a solid body.
Rearranging equation () by vector identities, multiplying both terms by "one", and grouping appropriately,
gives the total angular momentum of the system of particles in terms of
moment of inertia and
angular velocity ,
Single particle case
In the case of a single particle moving about the arbitrary origin,
and equations () and () for total angular momentum reduce to,
Case of a fixed center of mass
For the case of the center of mass fixed in space with respect to the origin,
and equations () and () for total angular momentum reduce to,
Angular momentum in general relativity

In modern (20th century) theoretical physics, angular momentum (not including any intrinsic angular momentum – see
below) is described using a different formalism, instead of a classical
pseudovector. In this formalism, angular momentum is the
2-form Noether charge associated with rotational invariance. As a result, angular momentum is generally not conserved locally for general
curved spacetimes, unless they have rotational symmetry;
[
] whereas globally the notion of angular momentum itself only makes sense if the spacetime is asymptotically flat.
[
] If the spacetime is only axially symmetric like for the
Kerr metric, the total angular momentum is not conserved but
is conserved which is related to the invariance of rotating around the symmetry-axis, where note that
where
is the
metric,
is the
rest mass,
is the
four-velocity, and
is the four-position in spherical coordinates.
In classical mechanics, the angular momentum of a particle can be reinterpreted as a plane element:
in which the
exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of ...
(∧) replaces the
cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
(×) (these products have similar characteristics but are nonequivalent). This has the advantage of a clearer geometric interpretation as a plane element, defined using the vectors x and p, and the expression is true in any number of dimensions. In Cartesian coordinates:
or more compactly in index notation:
The angular velocity can also be defined as an anti-symmetric second order tensor, with components ''ω
ij''. The relation between the two anti-symmetric tensors is given by the moment of inertia which must now be a fourth order tensor:
Again, this equation in L and ''ω'' as tensors is true in any number of dimensions. This equation also appears in the
geometric algebra formalism, in which L and ''ω'' are bivectors, and the moment of inertia is a mapping between them.
In
relativistic mechanics, the
relativistic angular momentum of a particle is expressed as an
anti-symmetric tensor of second order:
in terms of
four-vectors, namely the
four-position ''X'' and the
four-momentum ''P'', and absorbs the above L together with the
moment of mass, i.e., the product of the relativistic mass of the particle and its
center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
, which can be thought of as describing the motion of its center of mass, since mass–energy is conserved.
In each of the above cases, for a system of particles the total angular momentum is just the sum of the individual particle angular momenta, and the center of mass is for the system.
Angular momentum in quantum mechanics
In
quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, angular momentum (like other quantities) is expressed as an
operator, and its one-dimensional projections have
quantized eigenvalues. Angular momentum is subject to the
Heisenberg uncertainty principle, implying that at any time, only one
projection (also called "component") can be measured with definite precision; the other two then remain uncertain. Because of this, the axis of rotation of a quantum particle is undefined. Quantum particles ''do'' possess a type of non-orbital angular momentum called "spin", but this angular momentum does not correspond to a spinning motion. In
relativistic quantum mechanics the above relativistic definition becomes a tensorial operator.
Spin, orbital, and total angular momentum

The classical definition of angular momentum as
can be carried over to quantum mechanics, by reinterpreting r as the quantum
position operator and p as the quantum
momentum operator. L is then an
operator, specifically called the ''
orbital angular momentum operator''. The components of the angular momentum operator satisfy the commutation relations of the Lie algebra so(3). Indeed, these operators are precisely the infinitesimal action of the rotation group on the quantum
Hilbert space. (See also the discussion below of the angular momentum operators as the generators of rotations.)
However, in quantum physics, there is another type of angular momentum, called ''spin angular momentum'', represented by the spin operator S. Spin is often depicted as a particle literally spinning around an axis, but this is a misleading and inaccurate picture: spin is an intrinsic property of a particle, unrelated to any sort of motion in space and fundamentally different from orbital angular momentum. All
elementary particle
In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. The Standard Model presently recognizes seventeen distinct particles—twelve fermions and five bosons. As a c ...
s have a characteristic spin (possibly zero), and almost all
elementary particle
In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. The Standard Model presently recognizes seventeen distinct particles—twelve fermions and five bosons. As a c ...
s have nonzero spin. For example
electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
s have "spin 1/2" (this actually means "spin
ħ/2"),
photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s have "spin 1" (this actually means "spin ħ"), and
pi-mesons have spin 0.
Finally, there is
total angular momentum J, which combines both the spin and orbital angular momentum of all particles and fields. (For one particle, .)
Conservation of angular momentum applies to J, but not to L or S; for example, the
spin–orbit interaction allows angular momentum to transfer back and forth between L and S, with the total remaining constant. Electrons and photons need not have integer-based values for total angular momentum, but can also have half-integer values.
In molecules the total angular momentum F is the sum of the rovibronic (orbital) angular momentum N, the electron spin angular momentum S, and the nuclear spin angular momentum I. For electronic singlet states the rovibronic angular momentum is denoted J rather than N. As explained by Van Vleck, the components of the molecular rovibronic angular momentum referred to molecule-fixed axes have different commutation relations from those for the components about space-fixed axes.
Quantization
In
quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, angular momentum is
quantized – that is, it cannot vary continuously, but only in "
quantum leaps" between certain allowed values. For any system, the following restrictions on measurement results apply, where
is the
reduced Planck constant and
is any
Euclidean vector such as x, y, or z:

The
reduced Planck constant is tiny by everyday standards, about 10
−34 J s, and therefore this quantization does not noticeably affect the angular momentum of macroscopic objects. However, it is very important in the microscopic world. For example, the structure of
electron shells and subshells in chemistry is significantly affected by the quantization of angular momentum.
Quantization of angular momentum was first postulated by
Niels Bohr
Niels Henrik David Bohr (, ; ; 7 October 1885 – 18 November 1962) was a Danish theoretical physicist who made foundational contributions to understanding atomic structure and old quantum theory, quantum theory, for which he received the No ...
in
his model of the atom and was later predicted by
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger ( ; ; 12 August 1887 – 4 January 1961), sometimes written as or , was an Austrian-Irish theoretical physicist who developed fundamental results in quantum field theory, quantum theory. In particul ...
in his
Schrödinger equation.
Uncertainty
In the definition
, six operators are involved: The
position operators
,
,
, and the
momentum operators
,
,
. However, the
Heisenberg uncertainty principle tells us that it is not possible for all six of these quantities to be known simultaneously with arbitrary precision. Therefore, there are limits to what can be known or measured about a particle's angular momentum. It turns out that the best that one can do is to simultaneously measure both the angular momentum vector's
magnitude and its component along one axis.
The uncertainty is closely related to the fact that different components of an angular momentum operator do not
commute, for example
. (For the precise
commutation relations, see
angular momentum operator.)
Total angular momentum as generator of rotations
As mentioned above, orbital angular momentum L is defined as in classical mechanics:
, but ''total'' angular momentum J is defined in a different, more basic way: J is defined as the "generator of rotations".
More specifically, J is defined so that the operator
is the
rotation operator that takes any system and rotates it by angle
about the axis
. (The "exp" in the formula refers to
operator exponential.) To put this the other way around, whatever our quantum Hilbert space is, we expect that the
rotation group SO(3) will act on it. There is then an associated action of the Lie algebra so(3) of SO(3); the operators describing the action of so(3) on our Hilbert space are the (total) angular momentum operators.
The relationship between the angular momentum operator and the rotation operators is the same as the relationship between
Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi ident ...
s and
Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
s in mathematics. The close relationship between angular momentum and rotations is reflected in
Noether's theorem that proves that angular momentum is conserved whenever the laws of physics are rotationally invariant.
Angular momentum in electrodynamics
When describing the motion of a
charged particle in an
electromagnetic field, the
canonical momentum P (derived from the
Lagrangian for this system) is not
gauge invariant. As a consequence, the canonical angular momentum L = r × P is not gauge invariant either. Instead, the momentum that is physical, the so-called ''kinetic momentum'' (used throughout this article), is (in
SI units)
where ''e'' is the
electric charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and ...
of the particle and A the
magnetic vector potential
In classical electromagnetism, magnetic vector potential (often denoted A) is the vector quantity defined so that its curl is equal to the magnetic field, B: \nabla \times \mathbf = \mathbf. Together with the electric potential ''φ'', the ma ...
of the electromagnetic field. The gauge-invariant angular momentum, that is ''kinetic angular momentum'', is given by
The interplay with quantum mechanics is discussed further in the article on
canonical commutation relations.
Angular momentum in optics
In ''classical Maxwell electrodynamics'' the
Poynting vector
is a linear momentum density of electromagnetic field.
The angular momentum density vector
is given by a vector product
as in classical mechanics:
The above identities are valid ''locally'', i.e. in each space point
in a given moment
.
Angular momentum in nature and the cosmos
Tropical cyclones and other related weather phenomena involve conservation of angular momentum in order to explain the dynamics. Winds revolve slowly around low pressure systems, mainly due to the
coriolis effect. If the low pressure intensifies and the slowly circulating air is drawn toward the center, the molecules must speed up in order to conserve angular momentum. By the time they reach the center, the speeds become destructive.
Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
determined the laws of planetary motion without knowledge of conservation of momentum. However, not long after his discovery their derivation was determined from conservation of angular momentum. Planets move more slowly the further they are out in their elliptical orbits, which is explained intuitively by the fact that orbital angular momentum is proportional to the radius of the orbit. Since the mass does not change and the angular momentum is conserved, the velocity drops.
Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite (e.g. the
Moon
The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). The Moon rotation, rotates, with a rotation period (lunar ...
) and the primary planet that it orbits (e.g. Earth). The gravitational torque between the Moon and the tidal bulge of Earth causes the Moon to be constantly promoted to a slightly higher orbit (~3.8 cm per year) and Earth to be
decelerated (by −25.858 ± 0.003″/cy²) in its rotation (the
length of the day increases by ~1.7 ms per century, +2.3 ms from tidal effect and −0.6 ms from post-glacial rebound). The Earth loses angular momentum which is transferred to the Moon such that the overall angular momentum is conserved.
Angular momentum in engineering and technology
Examples of using conservation of angular momentum for practical advantage are abundant. In engines such as
steam engines or
internal combustion engines, a
flywheel is needed to efficiently convert the lateral motion of the pistons to rotational motion.
Inertial navigation system
An inertial navigation system (INS; also inertial guidance system, inertial instrument) is a navigation device that uses motion sensors (accelerometers), rotation sensors (gyroscopes) and a computer to continuously calculate by dead reckoning th ...
s explicitly use the fact that angular momentum is conserved with respect to the
inertial frame of space. Inertial navigation is what enables submarine trips under the polar ice cap, but are also crucial to all forms of modern navigation.
Rifled bullets use the stability provided by conservation of angular momentum to be more true in their trajectory. The invention of rifled firearms and cannons gave their users significant strategic advantage in battle, and thus were a technological turning point in history.
History
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
, in the
''Principia'', hinted at angular momentum in his examples of the
first law of motion,
A top, whose parts by their cohesion are perpetually drawn aside from rectilinear motions, does not cease its rotation, otherwise than as it is retarded by the air. The greater bodies of the planets and comets, meeting with less resistance in more free spaces, preserve their motions both progressive and circular for a much longer time.
He did not further investigate angular momentum directly in the ''Principia'', saying:
From such kind of reflexions also sometimes arise the circular motions of bodies about their own centers. But these are cases which I do not consider in what follows; and it would be too tedious to demonstrate every particular that relates to this subject.
However, his geometric proof of the
law of areas is an outstanding example of Newton's genius, and indirectly proves angular momentum conservation in the case of a
central force.
Law of Areas
Newton's derivation

As a
planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets b ...
orbits the
Sun, the line between the Sun and the planet sweeps out equal areas in equal intervals of time. This had been known since Kepler expounded his
second law of planetary motion. Newton derived a unique geometric proof, and went on to show that the attractive force of the Sun's
gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
was the cause of all of Kepler's laws.
During the first interval of time, an object is in motion from point A to point B. Undisturbed, it would continue to point c during the second interval. When the object arrives at B, it receives an impulse directed toward point S. The impulse gives it a small added velocity toward S, such that if this were its only velocity, it would move from B to V during the second interval. By the
rules of velocity composition, these two velocities add, and point C is found by construction of parallelogram BcCV. Thus the object's path is deflected by the impulse so that it arrives at point C at the end of the second interval. Because the triangles SBc and SBC have the same base SB and the same height Bc or VC, they have the same area. By symmetry, triangle SBc also has the same area as triangle SAB, therefore the object has swept out equal areas SAB and SBC in equal times.
At point C, the object receives another impulse toward S, again deflecting its path during the third interval from d to D. Thus it continues to E and beyond, the triangles SAB, SBc, SBC, SCd, SCD, SDe, SDE all having the same area. Allowing the time intervals to become ever smaller, the path ABCDE approaches indefinitely close to a continuous curve.
Note that because this derivation is geometric, and no specific force is applied, it proves a more general law than Kepler's second law of planetary motion. It shows that the Law of Areas applies to any central force, attractive or repulsive, continuous or non-continuous, or zero.
Conservation of angular momentum in the law of areas
The proportionality of angular momentum to the area swept out by a moving object can be understood by realizing that the bases of the triangles, that is, the lines from S to the object, are equivalent to the
radius , and that the heights of the triangles are proportional to the perpendicular component of
velocity . Hence, if the area swept per unit time is constant, then by the triangular area formula , the product and therefore the product are constant: if and the base length are decreased, and height must increase proportionally. Mass is constant, therefore
angular momentum is conserved by this exchange of distance and velocity.
In the case of triangle SBC, area is equal to (SB)(VC). Wherever C is eventually located due to the impulse applied at B, the product (SB)(VC), and therefore remain constant. Similarly so for each of the triangles.
Another areal proof of conservation of angular momentum for any central force uses Mamikon's sweeping tangents theorem.
After Newton
Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
,
Daniel Bernoulli, and
Patrick d'Arcy all understood angular momentum in terms of conservation of
areal velocity, a result of their analysis of Kepler's second law of planetary motion. It is unlikely that they realized the implications for ordinary rotating matter.
In 1736 Euler, like Newton, touched on some of the equations of angular momentum in his ''
Mechanica'' without further developing them.
Bernoulli wrote in a 1744 letter of a "moment of rotational motion", possibly the first conception of angular momentum as we now understand it.
In 1799,
Pierre-Simon Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
first realized that a fixed plane was associated with rotation—his ''
invariable plane''.
Louis Poinsot in 1803 began representing rotations as a line segment perpendicular to the rotation, and elaborated on the "conservation of moments".
In 1852
Léon Foucault used a
gyroscope in an experiment to display the Earth's rotation.
William J. M. Rankine's 1858 ''Manual of Applied Mechanics'' defined angular momentum in the modern sense for the first time:
... a line whose length is proportional to the magnitude of the angular momentum, and whose direction is perpendicular to the plane of motion of the body and of the fixed point, and such, that when the motion of the body is viewed from the extremity of the line, the radius-vector of the body seems to have right-handed rotation.
In an 1872 edition of the same book, Rankine stated that "The term ''angular momentum'' was introduced by Mr. Hayward," probably referring to R.B. Hayward's article ''On a Direct Method of estimating Velocities, Accelerations, and all similar Quantities with respect to Axes moveable in any manner in Space with Applications,''
which was introduced in 1856, and published in 1864. Rankine was mistaken, as numerous publications feature the term starting in the late 18th to early 19th centuries. However, Hayward's article apparently was the first use of the term and the concept seen by much of the English-speaking world. Before this, angular momentum was typically referred to as "momentum of rotation" in English.
[see, for instance, ]
See also
References
Further reading
*
*
*
* .
*
*
*
*
*
External links
"What Do a Submarine, a Rocket and a Football Have in Common?Why the prolate spheroid is the shape for success" (''Scientific American'', November 8, 2010)
– a chapter from an online textbook
– derivation of the three-dimensional case
Angular Momentum and Rolling Motion– more momentum theory
{{Authority control
Mechanical quantities
Rotation
Conservation laws
Moment (physics)
Angular momentum
 Angular momentum is a vector quantity (more precisely, a pseudovector) that represents the product of a body's rotational inertia and rotational velocity (in radians/sec) about a particular axis. However, if the particle's trajectory lies in a single plane, it is sufficient to discard the vector nature of angular momentum, and treat it as a scalar (more precisely, a pseudoscalar).
Angular momentum can be considered a rotational analog of linear momentum. Thus, where linear momentum is proportional to
Angular momentum is a vector quantity (more precisely, a pseudovector) that represents the product of a body's rotational inertia and rotational velocity (in radians/sec) about a particular axis. However, if the particle's trajectory lies in a single plane, it is sufficient to discard the vector nature of angular momentum, and treat it as a scalar (more precisely, a pseudoscalar).
Angular momentum can be considered a rotational analog of linear momentum. Thus, where linear momentum is proportional to  To completely define orbital angular momentum in three dimensions, it is required to know the rate at which the position vector sweeps out an angle, the direction perpendicular to the instantaneous plane of angular displacement, and the
To completely define orbital angular momentum in three dimensions, it is required to know the rate at which the position vector sweeps out an angle, the direction perpendicular to the instantaneous plane of angular displacement, and the  The above analogy of the translational momentum and rotational momentum can be expressed in vector form:
* for linear motion
* for rotation
The direction of momentum is related to the direction of the velocity for linear movement. The direction of angular momentum is related to the angular velocity of the rotation.
Because moment of inertia is a crucial part of the spin angular momentum, the latter necessarily includes all of the complications of the former, which is calculated by multiplying elementary bits of the mass by the
The above analogy of the translational momentum and rotational momentum can be expressed in vector form:
* for linear motion
* for rotation
The direction of momentum is related to the direction of the velocity for linear movement. The direction of angular momentum is related to the angular velocity of the rotation.
Because moment of inertia is a crucial part of the spin angular momentum, the latter necessarily includes all of the complications of the former, which is calculated by multiplying elementary bits of the mass by the  For a collection of particles in motion about an arbitrary origin, it is informative to develop the equation of angular momentum by resolving their motion into components about their own center of mass and about the origin. Given,
* is the mass of particle ,
* is the position vector of particle w.r.t. the origin,
* is the velocity of particle w.r.t. the origin,
* is the position vector of the center of mass w.r.t. the origin,
* is the velocity of the center of mass w.r.t. the origin,
* is the position vector of particle w.r.t. the center of mass,
* is the velocity of particle w.r.t. the center of mass,
The total mass of the particles is simply their sum,
The position vector of the center of mass is defined by,
By inspection,
: and
The total angular momentum of the collection of particles is the sum of the angular momentum of each particle,
Expanding ,
:
Expanding ,
:
It can be shown that (see sidebar),
: and
therefore the second and third terms vanish,
:
The first term can be rearranged,
:
and total angular momentum for the collection of particles is finally,
The first term is the angular momentum of the center of mass relative to the origin. Similar to ', below, it is the angular momentum of one particle of mass ''M'' at the center of mass moving with velocity V. The second term is the angular momentum of the particles moving relative to the center of mass, similar to ', below. The result is general—the motion of the particles is not restricted to rotation or revolution about the origin or center of mass. The particles need not be individual masses, but can be elements of a continuous distribution, such as a solid body.
Rearranging equation () by vector identities, multiplying both terms by "one", and grouping appropriately,
gives the total angular momentum of the system of particles in terms of moment of inertia and angular velocity ,
For a collection of particles in motion about an arbitrary origin, it is informative to develop the equation of angular momentum by resolving their motion into components about their own center of mass and about the origin. Given,
* is the mass of particle ,
* is the position vector of particle w.r.t. the origin,
* is the velocity of particle w.r.t. the origin,
* is the position vector of the center of mass w.r.t. the origin,
* is the velocity of the center of mass w.r.t. the origin,
* is the position vector of particle w.r.t. the center of mass,
* is the velocity of particle w.r.t. the center of mass,
The total mass of the particles is simply their sum,
The position vector of the center of mass is defined by,
By inspection,
: and
The total angular momentum of the collection of particles is the sum of the angular momentum of each particle,
Expanding ,
:
Expanding ,
:
It can be shown that (see sidebar),
: and
therefore the second and third terms vanish,
:
The first term can be rearranged,
:
and total angular momentum for the collection of particles is finally,
The first term is the angular momentum of the center of mass relative to the origin. Similar to ', below, it is the angular momentum of one particle of mass ''M'' at the center of mass moving with velocity V. The second term is the angular momentum of the particles moving relative to the center of mass, similar to ', below. The result is general—the motion of the particles is not restricted to rotation or revolution about the origin or center of mass. The particles need not be individual masses, but can be elements of a continuous distribution, such as a solid body.
Rearranging equation () by vector identities, multiplying both terms by "one", and grouping appropriately,
gives the total angular momentum of the system of particles in terms of moment of inertia and angular velocity ,
 The reduced Planck constant is tiny by everyday standards, about 10−34 J s, and therefore this quantization does not noticeably affect the angular momentum of macroscopic objects. However, it is very important in the microscopic world. For example, the structure of electron shells and subshells in chemistry is significantly affected by the quantization of angular momentum.
Quantization of angular momentum was first postulated by
The reduced Planck constant is tiny by everyday standards, about 10−34 J s, and therefore this quantization does not noticeably affect the angular momentum of macroscopic objects. However, it is very important in the microscopic world. For example, the structure of electron shells and subshells in chemistry is significantly affected by the quantization of angular momentum.
Quantization of angular momentum was first postulated by  As a
As a