group theory on:
[Wikipedia]
[Google]
[Amazon]
In
abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structur ...
, group theory studies the algebraic structure
In mathematics, an algebraic structure or algebraic system consists of a nonempty set ''A'' (called the underlying set, carrier set or domain), a collection of operations on ''A'' (typically binary operations such as addition and multiplicatio ...
s known as groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
s, can all be seen as groups endowed with additional operations and axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or ...
s. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n\times n matrices (under matrix multiplication) that is defined by polynomial equations. An example is the orthogonal group, defined by the relation M^TM = I_n ...
s and Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
s are two branches of group theory that have experienced advances and have become subject areas in their own right.
Various physical systems, such as crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
s and the hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a single positively charged proton in the nucleus, and a single negatively charged electron bound to the nucleus by the Coulomb for ...
, and three of the four known fundamental forces in the universe, may be modelled by symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
s. Thus group theory and the closely related representation theory
Representation theory is a branch of mathematics that studies abstract algebra, abstract algebraic structures by ''representing'' their element (set theory), elements as linear transformations of vector spaces, and studies Module (mathematics), ...
have many important applications in physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
, and materials science
Materials science is an interdisciplinary field of researching and discovering materials. Materials engineering is an engineering field of finding uses for materials in other fields and industries.
The intellectual origins of materials sci ...
. Group theory is also central to public key cryptography
Public-key cryptography, or asymmetric cryptography, is the field of cryptographic systems that use pairs of related keys. Each key pair consists of a public key and a corresponding private key. Key pairs are generated with cryptographic al ...
.
The early history of group theory
The history of group theory, a mathematical domain studying groups in their various forms, has evolved in various parallel threads. There are three historical roots of group theory: the theory of algebraic equations, number theory and geometry. Jo ...
dates from the 19th century. One of the most important mathematical achievements of the 20th century was the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 2004, that culminated in a complete classification of finite simple groups
In mathematics, the classification of finite simple groups (popularly called the enormous theorem) is a result of group theory stating that every List of finite simple groups, finite simple group is either cyclic group, cyclic, or alternating gro ...
.
History
Group theory has three main historical sources:number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
, the theory of algebraic equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form P = 0, where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers.
For example, x^5-3x+1=0 is an algebraic equati ...
s, and geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
. The number-theoretic strand was begun by Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
, and developed by Gauss's work on modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic operations for integers, other than the usual ones from elementary arithmetic, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to mo ...
and additive and multiplicative groups related to quadratic field
In algebraic number theory, a quadratic field is an algebraic number field of Degree of a field extension, degree two over \mathbf, the rational numbers.
Every such quadratic field is some \mathbf(\sqrt) where d is a (uniquely defined) square-free ...
s. Early results about permutation groups were obtained by Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaRuffini, and
 Geometric group theory attacks these problems from a geometric viewpoint, either by viewing groups as geometric objects, or by finding suitable geometric objects a group acts on. The first idea is made precise by means of the
Geometric group theory attacks these problems from a geometric viewpoint, either by viewing groups as geometric objects, or by finding suitable geometric objects a group acts on. The first idea is made precise by means of the

 In
In
 Very large groups of prime order constructed in
Very large groups of prime order constructed in
History of the abstract group concept
* This is a detailed exposition of contemporaneous understanding of Group Theory by an early researcher in the field. {{Authority control ml:ഗ്രൂപ്പ് സിദ്ധാന്തം
Abel
Abel ( ''Hébel'', in pausa ''Hā́ḇel''; ''Hábel''; , ''Hābēl'') is a biblical figure in the Book of Genesis within the Abrahamic religions. Born as the second son of Adam and Eve, the first two humans created by God in Judaism, God, he ...
in their quest for general solutions of polynomial equations of high degree. Évariste Galois
Évariste Galois (; ; 25 October 1811 – 31 May 1832) was a French mathematician and political activist. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by Nth root, ...
coined the term "group" and established a connection, now known as Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field (mathematics), field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems ...
, between the nascent theory of groups and field theory. In geometry, groups first became important in projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
and, later, non-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean ge ...
. Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
's Erlangen program
In mathematics, the Erlangen program is a method of characterizing geometries based on group theory and projective geometry. It was published by Felix Klein in 1872 as ''Vergleichende Betrachtungen über neuere geometrische Forschungen.'' It is na ...
proclaimed group theory to be the organizing principle of geometry.
Galois, in the 1830s, was the first to employ groups to determine the solvability of polynomial equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form P = 0, where ''P'' is a polynomial with coefficients in some field (mathematics), field, often the field of the rational numbers.
For example, x^5-3x+1=0 is a ...
s. Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics, and was a professor at Trinity College, Cambridge for 35 years.
He ...
and Augustin Louis Cauchy pushed these investigations further by creating the theory of permutation groups. The second historical source for groups stems from geometrical situations. In an attempt to come to grips with possible geometries (such as euclidean, hyperbolic
Hyperbolic may refer to:
* of or pertaining to a hyperbola, a type of smooth curve lying in a plane in mathematics
** Hyperbolic geometry, a non-Euclidean geometry
** Hyperbolic functions, analogues of ordinary trigonometric functions, defined u ...
or projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
) using group theory, Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
initiated the Erlangen programme. Sophus Lie
Marius Sophus Lie ( ; ; 17 December 1842 – 18 February 1899) was a Norwegian mathematician. He largely created the theory of continuous symmetry and applied it to the study of geometry and differential equations. He also made substantial cont ...
, in 1884, started using groups (now called Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
s) attached to analytic problems. Thirdly, groups were, at first implicitly and later explicitly, used in algebraic number theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic ob ...
.
The different scope of these early sources resulted in different notions of groups. The theory of groups was unified starting around 1880. Since then, the impact of group theory has been ever growing, giving rise to the birth of abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structur ...
in the early 20th century, representation theory
Representation theory is a branch of mathematics that studies abstract algebra, abstract algebraic structures by ''representing'' their element (set theory), elements as linear transformations of vector spaces, and studies Module (mathematics), ...
, and many more influential spin-off domains. The classification of finite simple groups
In mathematics, the classification of finite simple groups (popularly called the enormous theorem) is a result of group theory stating that every List of finite simple groups, finite simple group is either cyclic group, cyclic, or alternating gro ...
is a vast body of work from the mid 20th century, classifying all the finite simple group
SIMPLE Group Limited is a conglomeration of separately run companies that each has its core area in International Consulting. The core business areas are Legal Services, Fiduciary Activities, Banking Intermediation and Corporate Service.
The d ...
s.
Main classes of groups
The range of groups being considered has gradually expanded from finite permutation groups and special examples of matrix groups to abstract groups that may be specified through apresentation
A presentation conveys information from a speaker to an audience. Presentations are typically demonstrations, introduction, lecture, or speech meant to inform, persuade, inspire, motivate, build goodwill, or present a new idea/product. Presenta ...
by generators and relations.
Permutation groups
The firstclass
Class, Classes, or The Class may refer to:
Common uses not otherwise categorized
* Class (biology), a taxonomic rank
* Class (knowledge representation), a collection of individuals or objects
* Class (philosophy), an analytical concept used d ...
of groups to undergo a systematic study was permutation group
In mathematics, a permutation group is a group ''G'' whose elements are permutations of a given set ''M'' and whose group operation is the composition of permutations in ''G'' (which are thought of as bijective functions from the set ''M'' to ...
s. Given any set ''X'' and a collection ''G'' of bijection
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
s of ''X'' into itself (known as ''permutations'') that is closed under compositions and inverses, ''G'' is a group acting
Acting is an activity in which a story is told by means of its enactment by an actor who adopts a character—in theatre, television, film, radio, or any other medium that makes use of the mimetic mode.
Acting involves a broad range of sk ...
on ''X''. If ''X'' consists of ''n'' elements and ''G'' consists of ''all'' permutations, ''G'' is the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric grou ...
S''n''; in general, any permutation group ''G'' is a subgroup
In group theory, a branch of mathematics, a subset of a group G is a subgroup of G if the members of that subset form a group with respect to the group operation in G.
Formally, given a group (mathematics), group under a binary operation ...
of the symmetric group of ''X''. An early construction due to Cayley exhibited any group as a permutation group, acting on itself () by means of the left regular representation.
In many cases, the structure of a permutation group can be studied using the properties of its action on the corresponding set. For example, in this way one proves that for , the alternating group
In mathematics, an alternating group is the Group (mathematics), group of even permutations of a finite set. The alternating group on a set of elements is called the alternating group of degree , or the alternating group on letters and denoted ...
A''n'' is simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by John ...
, i.e. does not admit any proper normal subgroup
In abstract algebra, a normal subgroup (also known as an invariant subgroup or self-conjugate subgroup) is a subgroup that is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup N of the group ...
s. This fact plays a key role in the impossibility of solving a general algebraic equation of degree in radicals.
Matrix groups
The next important class of groups is given by ''matrix groups'', orlinear group In mathematics, a matrix group is a group ''G'' consisting of invertible matrices over a specified field ''K'', with the operation of matrix multiplication. A linear group is a group that is isomorphic to a matrix group (that is, admitting a ...
s. Here ''G'' is a set consisting of invertible matrices
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the ...
of given order ''n'' over a field ''K'' that is closed under the products and inverses. Such a group acts on the ''n''-dimensional vector space ''K''''n'' by linear transformation
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that pr ...
s. This action makes matrix groups conceptually similar to permutation groups, and the geometry of the action may be usefully exploited to establish properties of the group ''G''.
Transformation groups
Permutation groups and matrix groups are special cases oftransformation group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the gr ...
s: groups that act on a certain space ''X'' preserving its inherent structure. In the case of permutation groups, ''X'' is a set; for matrix groups, ''X'' is a vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
. The concept of a transformation group is closely related with the concept of a symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
: transformation groups frequently consist of ''all'' transformations that preserve a certain structure.
The theory of transformation groups forms a bridge connecting group theory with differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
. A long line of research, originating with Lie and Klein, considers group actions on manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
s by homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function ...
s or diffeomorphism
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
Definit ...
s. The groups themselves may be discrete
Discrete may refer to:
*Discrete particle or quantum in physics, for example in quantum theory
* Discrete device, an electronic component with just one circuit element, either passive or active, other than an integrated circuit
* Discrete group, ...
or continuous.
Abstract groups
Most groups considered in the first stage of the development of group theory were "concrete", having been realized through numbers, permutations, or matrices. It was not until the late nineteenth century that the idea of an abstract group began to take hold, where "abstract" means that the nature of the elements are ignored in such a way that two isomorphic groups are considered as the same group. A typical way of specifying an abstract group is through apresentation
A presentation conveys information from a speaker to an audience. Presentations are typically demonstrations, introduction, lecture, or speech meant to inform, persuade, inspire, motivate, build goodwill, or present a new idea/product. Presenta ...
by ''generators and relations'',
:
A significant source of abstract groups is given by the construction of a ''factor group'', or quotient group
A quotient group or factor group is a mathematical group obtained by aggregating similar elements of a larger group using an equivalence relation that preserves some of the group structure (the rest of the structure is "factored out"). For ex ...
, ''G''/''H'', of a group ''G'' by a normal subgroup
In abstract algebra, a normal subgroup (also known as an invariant subgroup or self-conjugate subgroup) is a subgroup that is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup N of the group ...
''H''. Class group
In mathematics, the ideal class group (or class group) of an algebraic number field K is the quotient group J_K/P_K where J_K is the group of fractional ideals of the ring of integers of K, and P_K is its subgroup of principal ideals. The class ...
s of algebraic number field
In mathematics, an algebraic number field (or simply number field) is an extension field K of the field of rational numbers such that the field extension K / \mathbb has finite degree (and hence is an algebraic field extension).
Thus K is a ...
s were among the earliest examples of factor groups, of much interest in number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
. If a group ''G'' is a permutation group on a set ''X'', the factor group ''G''/''H'' is no longer acting on ''X''; but the idea of an abstract group permits one not to worry about this discrepancy.
The change of perspective from concrete to abstract groups makes it natural to consider properties of groups that are independent of a particular realization, or in modern language, invariant under isomorphism
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
, as well as the classes of group with a given such property: finite group
In abstract algebra, a finite group is a group whose underlying set is finite. Finite groups often arise when considering symmetry of mathematical or physical objects, when those objects admit just a finite number of structure-preserving tra ...
s, periodic groups, simple group
SIMPLE Group Limited is a conglomeration of separately run companies that each has its core area in International Consulting. The core business areas are Legal Services, Fiduciary Activities, Banking Intermediation and Corporate Service.
The d ...
s, solvable group
In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminat ...
s, and so on. Rather than exploring properties of an individual group, one seeks to establish results that apply to a whole class of groups. The new paradigm was of paramount importance for the development of mathematics: it foreshadowed the creation of abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structur ...
in the works of Hilbert
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician and philosophy of mathematics, philosopher of mathematics and one of the most influential mathematicians of his time.
Hilbert discovered and developed a broad ...
, Emil Artin
Emil Artin (; March 3, 1898 – December 20, 1962) was an Austrians, Austrian mathematician of Armenians, Armenian descent.
Artin was one of the leading mathematicians of the twentieth century. He is best known for his work on algebraic number t ...
, Emmy Noether
Amalie Emmy Noether (23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's theorem, Noether's first and Noether's second theorem, second theorems, which ...
, and mathematicians of their school.
Groups with additional structure
An important elaboration of the concept of a group occurs if ''G'' is endowed with additional structure, notably, of atopological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
, differentiable manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One ...
, or algebraic variety
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the solution set, set of solutions of a system of polynomial equations over the real number, ...
. If the multiplication and inversion of the group are compatible with this structure, that is, they are continuous, smooth or regular (in the sense of algebraic geometry) maps, then ''G'' is a topological group
In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures ...
, a Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
, or an algebraic group.
The presence of extra structure relates these types of groups with other mathematical disciplines and means that more tools are available in their study. Topological groups form a natural domain for abstract harmonic analysis, whereas Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
s (frequently realized as transformation groups) are the mainstays of differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
and unitary representation theory
Representation theory is a branch of mathematics that studies abstract algebra, abstract algebraic structures by ''representing'' their element (set theory), elements as linear transformations of vector spaces, and studies Module (mathematics), ...
. Certain classification questions that cannot be solved in general can be approached and resolved for special subclasses of groups. Thus, compact connected Lie groups have been completely classified. There is a fruitful relation between infinite abstract groups and topological groups: whenever a group ''Γ'' can be realized as a lattice in a topological group ''G'', the geometry and analysis pertaining to ''G'' yield important results about ''Γ''. A comparatively recent trend in the theory of finite groups exploits their connections with compact topological groups ( profinite groups): for example, a single ''p''-adic analytic group ''G'' has a family of quotients which are finite ''p''-groups of various orders, and properties of ''G'' translate into the properties of its finite quotients.
Branches of group theory
Finite group theory
During the twentieth century, mathematicians investigated some aspects of the theory of finite groups in great depth, especially thelocal theory
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. A theory that includes the principle of locality is said to be a "local theory". This is an alternative to the concept of ins ...
of finite groups and the theory of solvable and nilpotent groups. As a consequence, the complete classification of finite simple groups
In mathematics, the classification of finite simple groups (popularly called the enormous theorem) is a result of group theory stating that every List of finite simple groups, finite simple group is either cyclic group, cyclic, or alternating gro ...
was achieved, meaning that all those simple group
SIMPLE Group Limited is a conglomeration of separately run companies that each has its core area in International Consulting. The core business areas are Legal Services, Fiduciary Activities, Banking Intermediation and Corporate Service.
The d ...
s from which all finite groups can be built are now known.
During the second half of the twentieth century, mathematicians such as Chevalley and Steinberg also increased our understanding of finite analogs of classical group
In mathematics, the classical groups are defined as the special linear groups over the reals \mathbb, the complex numbers \mathbb and the quaternions \mathbb together with special automorphism groups of Bilinear form#Symmetric, skew-symmetric an ...
s, and other related groups. One such family of groups is the family of general linear group
In mathematics, the general linear group of degree n is the set of n\times n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again inve ...
s over finite field
In mathematics, a finite field or Galois field (so-named in honor of Évariste Galois) is a field (mathematics), field that contains a finite number of Element (mathematics), elements. As with any field, a finite field is a Set (mathematics), s ...
s.
Finite groups often occur when considering symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
of mathematical or
physical objects, when those objects admit just a finite number of structure-preserving transformations. The theory of Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
s,
which may be viewed as dealing with "continuous symmetry
In mathematics, continuous symmetry is an intuitive idea corresponding to the concept of viewing some Symmetry in mathematics, symmetries as Motion (physics), motions, as opposed to discrete symmetry, e.g. reflection symmetry, which is invariant u ...
", is strongly influenced by the associated Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections t ...
s. These are finite groups generated by reflections which act on a finite-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. The properties of finite groups can thus play a role in subjects such as theoretical physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain, and predict List of natural phenomena, natural phenomena. This is in contrast to experimental p ...
and chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
.
Representation of groups
Saying that a group ''G'' '' acts'' on a set ''X'' means that every element of ''G'' defines a bijective map on the set ''X'' in a way compatible with the group structure. When ''X'' has more structure, it is useful to restrict this notion further: a representation of ''G'' on avector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
''V'' is a group homomorphism
In mathematics, given two groups, (''G'',∗) and (''H'', ·), a group homomorphism from (''G'',∗) to (''H'', ·) is a function ''h'' : ''G'' → ''H'' such that for all ''u'' and ''v'' in ''G'' it holds that
: h(u*v) = h(u) \cdot h(v)
whe ...
:
:
where GL(''V'') consists of the invertible linear transformations of ''V''. In other words, to every group element ''g'' is assigned an automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphism ...
''ρ''(''g'') such that for any ''h'' in ''G''.
This definition can be understood in two directions, both of which give rise to whole new domains of mathematics. On the one hand, it may yield new information about the group ''G'': often, the group operation in ''G'' is abstractly given, but via ''ρ'', it corresponds to the multiplication of matrices, which is very explicit. On the other hand, given a well-understood group acting on a complicated object, this simplifies the study of the object in question. For example, if ''G'' is finite, it is known that ''V'' above decomposes into irreducible parts (see Maschke's theorem). These parts, in turn, are much more easily manageable than the whole ''V'' (via Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if ''M'' and ''N'' are two finite-dimensional irreducible representations
of a gro ...
).
Given a group ''G'', representation theory
Representation theory is a branch of mathematics that studies abstract algebra, abstract algebraic structures by ''representing'' their element (set theory), elements as linear transformations of vector spaces, and studies Module (mathematics), ...
then asks what representations of ''G'' exist. There are several settings, and the employed methods and obtained results are rather different in every case: representation theory of finite groups
The representation theory of groups is a part of mathematics which examines how groups act on given structures.
Here the focus is in particular on operations of groups on vector spaces. Nevertheless, groups acting on other groups or on sets are ...
and representations of Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
s are two main subdomains of the theory. The totality of representations is governed by the group's characters. For example, Fourier polynomials can be interpreted as the characters of U(1)
In mathematics, the circle group, denoted by \mathbb T or , is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane or simply the unit complex numbers
\mathbb T = \.
The circle g ...
, the group of complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
of absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
''1'', acting on the ''L''2-space of periodic functions.
Lie theory
ALie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
is a group that is also a differentiable manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One ...
, with the property that the group operations are compatible with the smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows mathematical analysis to be performed on the manifold.
Definition
A smooth structure on a manifold M ...
. Lie groups are named after Sophus Lie
Marius Sophus Lie ( ; ; 17 December 1842 – 18 February 1899) was a Norwegian mathematician. He largely created the theory of continuous symmetry and applied it to the study of geometry and differential equations. He also made substantial cont ...
, who laid the foundations of the theory of continuous transformation group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the gr ...
s. The term ''groupes de Lie'' first appeared in French in 1893 in the thesis of Lie's student Arthur Tresse
Arthur is a masculine given name of uncertain etymology. Its popularity derives from it being the name of the legendary hero King Arthur.
A common spelling variant used in many Slavic, Romance, and Germanic languages is Artur. In Spanish and Ital ...
, page 3.
Lie groups represent the best-developed theory of continuous symmetry
In mathematics, continuous symmetry is an intuitive idea corresponding to the concept of viewing some Symmetry in mathematics, symmetries as Motion (physics), motions, as opposed to discrete symmetry, e.g. reflection symmetry, which is invariant u ...
of mathematical object
A mathematical object is an abstract concept arising in mathematics. Typically, a mathematical object can be a value that can be assigned to a Glossary of mathematical symbols, symbol, and therefore can be involved in formulas. Commonly encounter ...
s and structures, which makes them indispensable tools for many parts of contemporary mathematics, as well as for modern theoretical physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain, and predict List of natural phenomena, natural phenomena. This is in contrast to experimental p ...
. They provide a natural framework for analysing the continuous symmetries of differential equations ( differential Galois theory), in much the same way as permutation groups are used in Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field (mathematics), field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems ...
for analysing the discrete symmetries of algebraic equations
In mathematics, an algebraic equation or polynomial equation is an equation of the form P = 0, where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers.
For example, x^5-3x+1=0 is an algebraic equation ...
. An extension of Galois theory to the case of continuous symmetry groups was one of Lie's principal motivations.
Combinatorial and geometric group theory
Groups can be described in different ways. Finite groups can be described by writing down the group table consisting of all possible multiplications . A more compact way of defining a group is by ''generators and relations'', also called the ''presentation'' of a group. Given any set ''F'' of generators , thefree group
In mathematics, the free group ''F'S'' over a given set ''S'' consists of all words that can be built from members of ''S'', considering two words to be different unless their equality follows from the group axioms (e.g. ''st'' = ''suu''− ...
generated by ''F'' surjects onto the group ''G''. The kernel of this map is called the subgroup of relations, generated by some subset ''D''. The presentation is usually denoted by For example, the group presentation describes a group which is isomorphic to A string consisting of generator symbols and their inverses is called a ''word''.
Combinatorial group theory In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations. It is much used in geometric topology, the fundamental group of a simplicial complex having in a na ...
studies groups from the perspective of generators and relations. It is particularly useful where finiteness assumptions are satisfied, for example finitely generated groups, or finitely presented groups (i.e. in addition the relations are finite). The area makes use of the connection of graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
s via their fundamental group
In the mathematics, mathematical field of algebraic topology, the fundamental group of a topological space is the group (mathematics), group of the equivalence classes under homotopy of the Loop (topology), loops contained in the space. It record ...
s. A fundamental theorem of this area is that every subgroup of a free group is free.
There are several natural questions arising from giving a group by its presentation. The '' word problem'' asks whether two words are effectively the same group element. By relating the problem to Turing machine
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algori ...
s, one can show that there is in general no algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
solving this task. Another, generally harder, algorithmically insoluble problem is the group isomorphism problem, which asks whether two groups given by different presentations are actually isomorphic. For example, the group with presentation is isomorphic to the additive group Z of integers, although this may not be immediately apparent. (Writing , one has )
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
, whose vertices correspond to group elements and edges correspond to right multiplication in the group. Given two elements, one constructs the word metric given by the length of the minimal path between the elements. A theorem of Milnor and Svarc then says that given a group ''G'' acting in a reasonable manner on a metric space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...
''X'', for example a compact manifold
In mathematics, a closed manifold is a manifold Manifold with boundary, without boundary that is Compact space, compact.
In comparison, an open manifold is a manifold without boundary that has only ''non-compact'' components.
Examples
The onl ...
, then ''G'' is quasi-isometric (i.e. looks similar from a distance) to the space ''X''.
Connection of groups and symmetry
Given a structured object ''X'' of any sort, asymmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
is a mapping of the object onto itself which preserves the structure. This occurs in many cases, for example
*If ''X'' is a set with no additional structure, a symmetry is a bijective
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
map from the set to itself, giving rise to permutation groups.
*If the object ''X'' is a set of points in the plane with its metric
Metric or metrical may refer to:
Measuring
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
...
structure or any other metric space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...
, a symmetry is a bijection
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
of the set to itself which preserves the distance between each pair of points (an isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' me ...
). The corresponding group is called isometry group
In mathematics, the isometry group of a metric space is the set of all bijective isometries (that is, bijective, distance-preserving maps) from the metric space onto itself, with the function composition as group operation. Its identity element ...
of ''X''.
*If instead angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s are preserved, one speaks of conformal map
In mathematics, a conformal map is a function (mathematics), function that locally preserves angles, but not necessarily lengths.
More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-prese ...
s. Conformal maps give rise to Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of the group (mathematics), group of orientation-preserving Isometry, isometries of hyperbolic 3-space . The latter, identifiable with PSL(2,C), , is the quotient group of the 2 by 2 complex ...
s, for example.
*Symmetries are not restricted to geometrical objects, but include algebraic objects as well. For instance, the equation has the two solutions and . In this case, the group that exchanges the two roots is the Galois group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the pol ...
belonging to the equation. Every polynomial equation in one variable has a Galois group, that is a certain permutation group on its roots.
The axioms of a group formalize the essential aspects of symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
. Symmetries form a group: they are closed because if you take a symmetry of an object, and then apply another symmetry, the result will still be a symmetry. The identity keeping the object fixed is always a symmetry of an object. Existence of inverses is guaranteed by undoing the symmetry and the associativity comes from the fact that symmetries are functions on a space, and composition of functions is associative.
Frucht's theorem says that every group is the symmetry group of some graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
. So every abstract group is actually the symmetries of some explicit object.
The saying of "preserving the structure" of an object can be made precise by working in a category
Category, plural categories, may refer to:
General uses
*Classification, the general act of allocating things to classes/categories Philosophy
* Category of being
* ''Categories'' (Aristotle)
* Category (Kant)
* Categories (Peirce)
* Category ( ...
. Maps preserving the structure are then the morphism
In mathematics, a morphism is a concept of category theory that generalizes structure-preserving maps such as homomorphism between algebraic structures, functions from a set to another set, and continuous functions between topological spaces. Al ...
s, and the symmetry group is the automorphism group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the g ...
of the object in question.
Applications of group theory
Applications of group theory abound. Almost all structures inabstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structur ...
are special cases of groups. Rings, for example, can be viewed as abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commu ...
s (corresponding to addition) together with a second operation (corresponding to multiplication). Therefore, group theoretic arguments underlie large parts of the theory of those entities.
Galois theory
Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field (mathematics), field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems ...
uses groups to describe the symmetries of the roots of a polynomial (or more precisely the automorphisms of the algebras generated by these roots). The fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions in relation to groups. It was proved by Évariste Galois in his development of Galois theory.
In its most bas ...
provides a link between algebraic field extension
In mathematics, an algebraic extension is a field extension such that every element of the larger field is algebraic over the smaller field ; that is, every element of is a root of a non-zero polynomial with coefficients in . A field extens ...
s and group theory. It gives an effective criterion for the solvability of polynomial equations in terms of the solvability of the corresponding Galois group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the pol ...
. For example, ''S''5, the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric grou ...
in 5 elements, is not solvable which implies that the general quintic equation
In mathematics, a quintic function is a function of the form
:g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\,
where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other word ...
cannot be solved by radicals in the way equations of lower degree can. The theory, being one of the historical roots of group theory, is still fruitfully applied to yield new results in areas such as class field theory
In mathematics, class field theory (CFT) is the fundamental branch of algebraic number theory whose goal is to describe all the abelian Galois extensions of local and global fields using objects associated to the ground field.
Hilbert is credit ...
.
Algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
is another domain which prominently associates groups to the objects the theory is interested in. There, groups are used to describe certain invariants of topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
s. They are called "invariants" because they are defined in such a way that they do not change if the space is subjected to some deformation. For example, the fundamental group
In the mathematics, mathematical field of algebraic topology, the fundamental group of a topological space is the group (mathematics), group of the equivalence classes under homotopy of the Loop (topology), loops contained in the space. It record ...
"counts" how many paths in the space are essentially different. The Poincaré conjecture
In the mathematical field of geometric topology, the Poincaré conjecture (, , ) is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.
Originally conjectured b ...
, proved in 2002/2003 by Grigori Perelman, is a prominent application of this idea. The influence is not unidirectional, though. For example, algebraic topology makes use of Eilenberg–MacLane spaces which are spaces with prescribed homotopy groups
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted \pi_1(X), which records information about Loop (topology), loops in a Mathematic ...
. Similarly algebraic K-theory relies in a way on classifying space
In mathematics, specifically in homotopy theory, a classifying space ''BG'' of a topological group ''G'' is the quotient of a weakly contractible space ''EG'' (i.e., a topological space all of whose homotopy groups are trivial) by a proper free ...
s of groups. Finally, the name of the torsion subgroup
In the theory of abelian groups, the torsion subgroup ''AT'' of an abelian group ''A'' is the subgroup of ''A'' consisting of all elements that have finite order (the torsion elements of ''A''). An abelian group ''A'' is called a torsion group ...
of an infinite group shows the legacy of topology in group theory.

Algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
likewise uses group theory in many ways. Abelian varieties have been introduced above. The presence of the group operation yields additional information which makes these varieties particularly accessible. They also often serve as a test for new conjectures. (For example the Hodge conjecture (in certain cases).) The one-dimensional case, namely elliptic curve
In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point . An elliptic curve is defined over a field and describes points in , the Cartesian product of with itself. If the ...
s is studied in particular detail. They are both theoretically and practically intriguing. In another direction, toric varieties are algebraic varieties
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. ...
acted on by a torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
. Toroidal embeddings have recently led to advances in algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
, in particular resolution of singularities
In algebraic geometry, the problem of resolution of singularities asks whether every algebraic variety ''V'' has a resolution, which is a non-singular variety ''W'' with a Proper morphism, proper birational map ''W''→''V''. For varieties ov ...
.
Algebraic number theory
Algebraic number theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic ob ...
makes uses of groups for some important applications. For example, Euler's product formula,
:
captures the fact that any integer decomposes in a unique way into primes. The failure of this statement for more general rings gives rise to class group
In mathematics, the ideal class group (or class group) of an algebraic number field K is the quotient group J_K/P_K where J_K is the group of fractional ideals of the ring of integers of K, and P_K is its subgroup of principal ideals. The class ...
s and regular primes, which feature in Kummer's treatment of Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive number, positive integers , , and satisfy the equation for any integer value of greater than . The cases ...
.
Harmonic analysis
Analysis on Lie groups and certain other groups is calledharmonic analysis
Harmonic analysis is a branch of mathematics concerned with investigating the connections between a function and its representation in frequency. The frequency representation is found by using the Fourier transform for functions on unbounded do ...
. Haar measure
In mathematical analysis, the Haar measure assigns an "invariant volume" to subsets of locally compact topological groups, consequently defining an integral for functions on those groups.
This Measure (mathematics), measure was introduced by Alfr� ...
s, that is, integrals invariant under the translation in a Lie group, are used for pattern recognition
Pattern recognition is the task of assigning a class to an observation based on patterns extracted from data. While similar, pattern recognition (PR) is not to be confused with pattern machines (PM) which may possess PR capabilities but their p ...
and other image processing
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a pr ...
techniques.
Combinatorics
Incombinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many ...
, the notion of permutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
group and the concept of group action are often used to simplify the counting of a set of objects; see in particular Burnside's lemma.

Music
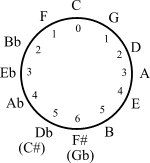
The presence of the 12- periodicity in thecircle of fifths
In music theory, the circle of fifths (sometimes also cycle of fifths) is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music (12-tone equal temperament), the se ...
yields applications of elementary group theory in musical set theory
Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonality, tonal music. Other theorists, such as Allen Forte, further devel ...
. Transformational theory
Transformational theory is a branch of music theory developed by David Lewin in the 1980s, and formally introduced in his 1987 work ''Generalized Musical Intervals and Transformations''. The theory—which models Transformation (music), musical t ...
models musical transformations as elements of a mathematical group.
Physics
Inphysics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, groups are important because they describe the symmetries which the laws of physics seem to obey. According to Noether's theorem
Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems (see Noether's second theorem) published by the mat ...
, every continuous symmetry of a physical system corresponds to a conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of mass-energy, conservation of linear momen ...
of the system. Physicists are very interested in group representations, especially of Lie groups, since these representations often point the way to the "possible" physical theories. Examples of the use of groups in physics include the Standard Model
The Standard Model of particle physics is the Scientific theory, theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions – excluding gravity) in the unive ...
, gauge theory
In physics, a gauge theory is a type of field theory in which the Lagrangian, and hence the dynamics of the system itself, does not change under local transformations according to certain smooth families of operations (Lie groups). Formally, t ...
, the Lorentz group
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physi ...
, and the Poincaré group.
Group theory can be used to resolve the incompleteness of the statistical interpretations of mechanics developed by Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynami ...
, relating to the summing of an infinite number of probabilities to yield a meaningful solution.Norbert Wiener
Norbert Wiener (November 26, 1894 – March 18, 1964) was an American computer scientist, mathematician, and philosopher. He became a professor of mathematics at the Massachusetts Institute of Technology ( MIT). A child prodigy, Wiener late ...
, Cybernetics: Or Control and Communication in the Animal and the Machine, , Ch 2
Chemistry and materials science
Inchemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
and materials science
Materials science is an interdisciplinary field of researching and discovering materials. Materials engineering is an engineering field of finding uses for materials in other fields and industries.
The intellectual origins of materials sci ...
, point group
In geometry, a point group is a group (mathematics), mathematical group of symmetry operations (isometry, isometries in a Euclidean space) that have a Fixed point (mathematics), fixed point in common. The Origin (mathematics), coordinate origin o ...
s are used to classify regular polyhedra, and the symmetries of molecules, and space group
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of the pattern that ...
s to classify crystal structure
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat ...
s. The assigned groups can then be used to determine physical properties (such as chemical polarity
In chemistry, polarity is a separation of electric charge leading to a molecule or its chemical groups having an electric dipole moment, with a negatively charged end and a positively charged end.
Polar molecules must contain one or more polar ...
and chirality
Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is distinguishable fro ...
), spectroscopic properties (particularly useful for Raman spectroscopy
Raman spectroscopy () (named after physicist C. V. Raman) is a Spectroscopy, spectroscopic technique typically used to determine vibrational modes of molecules, although rotational and other low-frequency modes of systems may also be observed. Ra ...
, infrared spectroscopy
Infrared spectroscopy (IR spectroscopy or vibrational spectroscopy) is the measurement of the interaction of infrared radiation with matter by absorption, emission, or reflection. It is used to study and identify chemical substances or functio ...
, circular dichroism spectroscopy, magnetic circular dichroism spectroscopy, UV/Vis spectroscopy, and fluorescence spectroscopy), and to construct molecular orbitals.
Molecular symmetry
In chemistry, molecular symmetry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explai ...
is responsible for many physical and spectroscopic properties of compounds and provides relevant information about how chemical reactions occur. In order to assign a point group for any given molecule, it is necessary to find the set of symmetry operations present on it. The symmetry operation is an action, such as a rotation around an axis or a reflection through a mirror plane. In other words, it is an operation that moves the molecule such that it is indistinguishable from the original configuration. In group theory, the rotation axes and mirror planes are called "symmetry elements". These elements can be a point, line or plane with respect to which the symmetry operation is carried out. The symmetry operations of a molecule determine the specific point group for this molecule.
 In
In chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
, there are five important symmetry operations. They are identity operation (E), rotation operation or proper rotation (C''n''), reflection operation (σ), inversion (i) and rotation reflection operation or improper rotation (S''n''). The identity operation (E) consists of leaving the molecule as it is. This is equivalent to any number of full rotations around any axis. This is a symmetry of all molecules, whereas the symmetry group of a chiral
Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek language, Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is dist ...
molecule consists of only the identity operation. An identity operation is a characteristic of every molecule even if it has no symmetry. Rotation around an axis (C''n'') consists of rotating the molecule around a specific axis by a specific angle. It is rotation through the angle 360°/''n'', where ''n'' is an integer, about a rotation axis. For example, if a water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
molecule rotates 180° around the axis that passes through the oxygen
Oxygen is a chemical element; it has chemical symbol, symbol O and atomic number 8. It is a member of the chalcogen group (periodic table), group in the periodic table, a highly reactivity (chemistry), reactive nonmetal (chemistry), non ...
atom and between the hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
atoms, it is in the same configuration as it started. In this case, , since applying it twice produces the identity operation. In molecules with more than one rotation axis, the Cn axis having the largest value of n is the highest order rotation axis or principal axis. For example in boron trifluoride (BF3), the highest order of rotation axis is C3, so the principal axis of rotation is C3.
In the reflection operation (σ) many molecules have mirror planes, although they may not be obvious. The reflection operation exchanges left and right, as if each point had moved perpendicularly through the plane to a position exactly as far from the plane as when it started. When the plane is perpendicular to the principal axis of rotation, it is called σ''h'' (horizontal). Other planes, which contain the principal axis of rotation, are labeled vertical (σ''v'') or dihedral (σ''d'').
Inversion (i ) is a more complex operation. Each point moves through the center of the molecule to a position opposite the original position and as far from the central point as where it started. Many molecules that seem at first glance to have an inversion center do not; for example, methane
Methane ( , ) is a chemical compound with the chemical formula (one carbon atom bonded to four hydrogen atoms). It is a group-14 hydride, the simplest alkane, and the main constituent of natural gas. The abundance of methane on Earth makes ...
and other tetrahedral
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
molecules lack inversion symmetry. To see this, hold a methane model with two hydrogen atoms in the vertical plane on the right and two hydrogen atoms in the horizontal plane on the left. Inversion results in two hydrogen atoms in the horizontal plane on the right and two hydrogen atoms in the vertical plane on the left. Inversion is therefore not a symmetry operation of methane, because the orientation of the molecule following the inversion operation differs from the original orientation. And the last operation is improper rotation or rotation reflection operation (S''n'') requires rotation of 360°/''n'', followed by reflection through a plane perpendicular to the axis of rotation.
Cryptography
elliptic curve cryptography
Elliptic-curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. ECC allows smaller keys to provide equivalent security, compared to cryptosystems based on modula ...
serve for public-key cryptography
Public-key cryptography, or asymmetric cryptography, is the field of cryptographic systems that use pairs of related keys. Each key pair consists of a public key and a corresponding private key. Key pairs are generated with cryptographic alg ...
. Cryptographical methods of this kind benefit from the flexibility of the geometric objects, hence their group structures, together with the complicated structure of these groups, which make the discrete logarithm
In mathematics, for given real numbers a and b, the logarithm \log_b(a) is a number x such that b^x=a. Analogously, in any group G, powers b^k can be defined for all integers k, and the discrete logarithm \log_b(a) is an integer k such that b^k=a ...
very hard to calculate. One of the earliest encryption protocols, Caesar's cipher, may also be interpreted as a (very easy) group operation. Most cryptographic schemes use groups in some way. In particular Diffie–Hellman key exchange
Diffie–Hellman (DH) key exchangeSynonyms of Diffie–Hellman key exchange include:
* Diffie–Hellman–Merkle key exchange
* Diffie–Hellman key agreement
* Diffie–Hellman key establishment
* Diffie–Hellman key negotiation
* Exponential ke ...
uses finite cyclic group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, ge ...
s. So the term group-based cryptography refers mostly to cryptographic protocol
A cryptographic protocol is an abstract or concrete Communications protocol, protocol that performs a information security, security-related function and applies cryptographic methods, often as sequences of cryptographic primitives. A protocol desc ...
s that use infinite non-abelian groups such as a braid group
In mathematics, the braid group on strands (denoted B_n), also known as the Artin braid group, is the group whose elements are equivalence classes of Braid theory, -braids (e.g. under ambient isotopy), and whose group operation is composition of ...
.
See also
* List of group theory topics * Examples of groups * Bass-Serre theoryNotes
References
* * * * * Shows the advantage of generalising from group togroupoid
In mathematics, especially in category theory and homotopy theory, a groupoid (less often Brandt groupoid or virtual group) generalises the notion of group in several equivalent ways. A groupoid can be seen as a:
* '' Group'' with a partial fu ...
.
* An introductory undergraduate text in the spirit of texts by Gallian or Herstein, covering groups, rings, integral domains, fields and Galois theory. Free downloadable PDF with open-source GFDL license.
*
*
* Conveys the practical value of group theory by explaining how it points to symmetries in physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
and other sciences.
*
* Ronan M., 2006. ''Symmetry and the Monster''. Oxford University Press. . For lay readers. Describes the quest to find the basic building blocks for finite groups.
* A standard contemporary reference.
*
* Inexpensive and fairly readable, but somewhat dated in emphasis, style, and notation.
*
*
External links
History of the abstract group concept
* This is a detailed exposition of contemporaneous understanding of Group Theory by an early researcher in the field. {{Authority control ml:ഗ്രൂപ്പ് സിദ്ധാന്തം