turbulent mixing on:
[Wikipedia]
[Google]
[Amazon]
In

 * Smoke rising from a
* Smoke rising from a
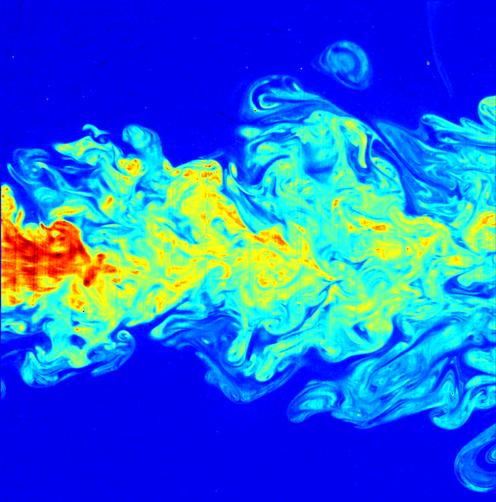 Turbulence is characterized by the following features:
; Irregularity : Turbulent flows are always highly irregular. For this reason, turbulence problems are normally treated statistically rather than deterministically. Turbulent flow is chaotic. However, not all chaotic flows are turbulent.
; Diffusivity :The readily available supply of energy in turbulent flows tends to accelerate the homogenization (mixing) of fluid mixtures. The characteristic which is responsible for the enhanced mixing and increased rates of mass, momentum and energy transports in a flow is called "diffusivity".
''Turbulent diffusion'' is usually described by a turbulent
Turbulence is characterized by the following features:
; Irregularity : Turbulent flows are always highly irregular. For this reason, turbulence problems are normally treated statistically rather than deterministically. Turbulent flow is chaotic. However, not all chaotic flows are turbulent.
; Diffusivity :The readily available supply of energy in turbulent flows tends to accelerate the homogenization (mixing) of fluid mixtures. The characteristic which is responsible for the enhanced mixing and increased rates of mass, momentum and energy transports in a flow is called "diffusivity".
''Turbulent diffusion'' is usually described by a turbulent
 The onset of turbulence can be, to some extent, predicted by the
The onset of turbulence can be, to some extent, predicted by the
Center for Turbulence Research
Scientific papers and books on turbulence
Center for Turbulence Research
Scientific American article
Air Turbulence Forecast
international CFD database iCFDdatabase
*
Fluid Mechanics website with movies, Q&A, etcJohns Hopkins public database with direct numerical simulation data TurBase public database with experimental data from European High Performance Infrastructures in Turbulence (EuHIT)
{{Authority control Concepts in physics Aerodynamics Chaos theory Transport phenomena Fluid dynamics Flow regimes
fluid dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) an ...
, turbulence or turbulent flow is fluid motion characterized by chaotic
Chaotic was originally a Danish trading card game. It expanded to an online game in America which then became a television program based on the game. The program was able to be seen on 4Kids TV (Fox affiliates, nationwide), Jetix, The CW4Kid ...
changes in pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and e ...
and flow velocity. It is in contrast to a laminar flow
In fluid dynamics, laminar flow is characterized by fluid particles following smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mi ...
, which occurs when a fluid flows in parallel layers, with no disruption between those layers.
Turbulence is commonly observed in everyday phenomena such as surf, fast flowing rivers, billowing storm clouds, or smoke from a chimney, and most fluid flows occurring in nature or created in engineering applications are turbulent. Turbulence is caused by excessive kinetic energy in parts of a fluid flow, which overcomes the damping effect of the fluid's viscosity. For this reason turbulence is commonly realized in low viscosity fluids. In general terms, in turbulent flow, unsteady vortices
In fluid dynamics, a vortex ( : vortices or vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in th ...
appear of many sizes which interact with each other, consequently drag due to friction effects increases. This increases the energy needed to pump fluid through a pipe.
The onset of turbulence can be predicted by the dimensionless Reynolds number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be domi ...
, the ratio of kinetic energy to viscous damping in a fluid flow. However, turbulence has long resisted detailed physical analysis, and the interactions within turbulence create a very complex phenomenon. Richard Feynman described turbulence as the most important unsolved problem in classical physics.
The turbulence intensity affects many fields, for examples fish ecology, air pollution, precipitation, and climate change.
Examples of turbulence

 * Smoke rising from a
* Smoke rising from a cigarette
A cigarette is a narrow cylinder containing a combustible material, typically tobacco, that is rolled into thin paper for smoking. The cigarette is ignited at one end, causing it to smolder; the resulting smoke is orally inhaled via the opp ...
. For the first few centimeters, the smoke is laminar
Laminar means "flat". Laminar may refer to:
Terms in science and engineering:
* Laminar electronics or organic electronics, a branch of material sciences dealing with electrically conductive polymers and small molecules
* Laminar armour or "band ...
. The smoke plume becomes turbulent as its Reynolds number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be domi ...
increases with increases in flow velocity and characteristic length scale.
* Flow over a golf ball. (This can be best understood by considering the golf ball to be stationary, with air flowing over it.) If the golf ball were smooth, the boundary layer flow over the front of the sphere would be laminar at typical conditions. However, the boundary layer would separate early, as the pressure gradient switched from favorable (pressure decreasing in the flow direction) to unfavorable (pressure increasing in the flow direction), creating a large region of low pressure behind the ball that creates high form drag. To prevent this, the surface is dimpled to perturb the boundary layer and promote turbulence. This results in higher skin friction, but it moves the point of boundary layer separation further along, resulting in lower drag.
* Clear-air turbulence experienced during airplane flight, as well as poor astronomical seeing (the blurring of images seen through the atmosphere).
* Most of the terrestrial atmospheric circulation.
* The oceanic and atmospheric mixed layers and intense oceanic currents.
* The flow conditions in many industrial equipment (such as pipes, ducts, precipitators, gas scrubber
Scrubber systems (e.g. chemical scrubbers, gas scrubbers) are a diverse group of air pollution control devices that can be used to remove some particulates and/or gases from industrial exhaust streams. An early application of a carbon dioxide scr ...
s, dynamic scraped surface heat exchangers, etc.) and machines (for instance, internal combustion engine
An internal combustion engine (ICE or IC engine) is a heat engine in which the combustion of a fuel occurs with an oxidizer (usually air) in a combustion chamber that is an integral part of the working fluid flow circuit. In an internal combus ...
s and gas turbines).
* The external flow over all kinds of vehicles such as cars, airplanes, ships, and submarines.
* The motions of matter in stellar atmospheres.
* A jet exhausting from a nozzle into a quiescent fluid. As the flow emerges into this external fluid, shear layers originating at the lips of the nozzle are created. These layers separate the fast moving jet from the external fluid, and at a certain critical Reynolds number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be domi ...
they become unstable and break down to turbulence.
* Biologically generated turbulence resulting from swimming animals affects ocean mixing.
* Snow fence
A snow fence, similar to a sand fence, is a barrier that forces windblown, drifting snow to accumulate in a desired place. They are primarily employed to minimize the amount of snowdrift on roadways and railways. Farmers and ranchers use snow fe ...
s work by inducing turbulence in the wind, forcing it to drop much of its snow load near the fence.
* Bridge supports (piers) in water. When river flow is slow, water flows smoothly around the support legs. When the flow is faster, a higher Reynolds number is associated with the flow. The flow may start off laminar but is quickly separated from the leg and becomes turbulent.
* In many geophysical flows (rivers, atmospheric boundary layer), the flow turbulence is dominated by the coherent structures and turbulent events. A turbulent event is a series of turbulent fluctuations that contain more energy than the average flow turbulence. The turbulent events are associated with coherent flow structures such as eddies and turbulent bursting, and they play a critical role in terms of sediment scour, accretion and transport in rivers as well as contaminant mixing and dispersion in rivers and estuaries, and in the atmosphere.
*In the medical field of cardiology
Cardiology () is a branch of medicine that deals with disorders of the heart and the cardiovascular system. The field includes medical diagnosis and treatment of congenital heart defects, coronary artery disease, heart failure, valvular heart d ...
, a stethoscope is used to detect heart sounds
Heart sounds are the noises generated by the beating heart and the resultant flow of blood through it. Specifically, the sounds reflect the turbulence created when the heart valves snap shut. In cardiac auscultation, an examiner may use a stetho ...
and bruits
Bruit, also called vascular murmur, is the abnormal sound generated by turbulent flow of blood in an artery due to either an area of partial obstruction or a localized high rate of blood flow through an unobstructed artery.
The bruit may be hear ...
, which are due to turbulent blood flow. In normal individuals, heart sounds are a product of turbulent flow as heart valves close. However, in some conditions turbulent flow can be audible due to other reasons, some of them pathological. For example, in advanced atherosclerosis, bruits (and therefore turbulent flow) can be heard in some vessels that have been narrowed by the disease process.
* Recently, turbulence in porous media became a highly debated subject.
Features
 Turbulence is characterized by the following features:
; Irregularity : Turbulent flows are always highly irregular. For this reason, turbulence problems are normally treated statistically rather than deterministically. Turbulent flow is chaotic. However, not all chaotic flows are turbulent.
; Diffusivity :The readily available supply of energy in turbulent flows tends to accelerate the homogenization (mixing) of fluid mixtures. The characteristic which is responsible for the enhanced mixing and increased rates of mass, momentum and energy transports in a flow is called "diffusivity".
''Turbulent diffusion'' is usually described by a turbulent
Turbulence is characterized by the following features:
; Irregularity : Turbulent flows are always highly irregular. For this reason, turbulence problems are normally treated statistically rather than deterministically. Turbulent flow is chaotic. However, not all chaotic flows are turbulent.
; Diffusivity :The readily available supply of energy in turbulent flows tends to accelerate the homogenization (mixing) of fluid mixtures. The characteristic which is responsible for the enhanced mixing and increased rates of mass, momentum and energy transports in a flow is called "diffusivity".
''Turbulent diffusion'' is usually described by a turbulent diffusion coefficient
Diffusivity, mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion). Diffusivity is enco ...
. This turbulent diffusion coefficient is defined in a phenomenological sense, by analogy with the molecular diffusivities, but it does not have a true physical meaning, being dependent on the flow conditions, and not a property of the fluid itself. In addition, the turbulent diffusivity concept assumes a constitutive relation between a turbulent flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport ph ...
and the gradient of a mean variable similar to the relation between flux and gradient that exists for molecular transport. In the best case, this assumption is only an approximation. Nevertheless, the turbulent diffusivity is the simplest approach for quantitative analysis of turbulent flows, and many models have been postulated to calculate it. For instance, in large bodies of water like oceans this coefficient can be found using Richardson
Richardson may refer to:
People
* Richardson (surname), an English and Scottish surname
* Richardson Gang, a London crime gang in the 1960s
* Richardson Dilworth, Mayor of Philadelphia (1956-1962)
Places Australia
* Richardson, Australian Cap ...
's four-third power law and is governed by the random walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...
principle. In rivers and large ocean currents, the diffusion coefficient is given by variations of Elder's formula.
; Rotationality :Turbulent flows have non-zero vorticity and are characterized by a strong three-dimensional vortex generation mechanism known as vortex stretching
In fluid dynamics, vortex stretching is the lengthening of vortices in three-dimensional fluid flow, associated with a corresponding increase of the component of vorticity in the stretching direction—due to the conservation of angular momentum. ...
. In fluid dynamics, they are essentially vortices subjected to stretching associated with a corresponding increase of the component of vorticity in the stretching direction—due to the conservation of angular momentum. On the other hand, vortex stretching is the core mechanism on which the turbulence energy cascade relies to establish and maintain identifiable structure function.Kundu, Pijush K.; Cohen, Ira M.; Dowling, David R. (2012). ''Fluid Mechanics''. Netherlands: Elsevier Inc. pp. 537–601. . In general, the stretching mechanism implies thinning of the vortices in the direction perpendicular to the stretching direction due to volume conservation of fluid elements. As a result, the radial length scale of the vortices decreases and the larger flow structures break down into smaller structures. The process continues until the small scale structures are small enough that their kinetic energy can be transformed by the fluid's molecular viscosity into heat. Turbulent flow is always rotational and three dimensional. For example, atmospheric cyclones are rotational but their substantially two-dimensional shapes do not allow vortex generation and so are not turbulent. On the other hand, oceanic flows are dispersive but essentially non rotational and therefore are not turbulent.
; Dissipation : To sustain turbulent flow, a persistent source of energy supply is required because turbulence dissipates rapidly as the kinetic energy is converted into internal energy by viscous shear stress. Turbulence causes the formation of eddies
In fluid dynamics, an eddy is the swirling of a fluid and the reverse current created when the fluid is in a turbulent flow regime. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object. Fluid beh ...
of many different length scales. Most of the kinetic energy of the turbulent motion is contained in the large-scale structures. The energy "cascades" from these large-scale structures to smaller scale structures by an inertial and essentially inviscid
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the inte ...
mechanism. This process continues, creating smaller and smaller structures which produces a hierarchy of eddies. Eventually this process creates structures that are small enough that molecular diffusion becomes important and viscous dissipation of energy finally takes place. The scale at which this happens is the Kolmogorov length scale.
Via this energy cascade, turbulent flow can be realized as a superposition of a spectrum of flow velocity fluctuations and eddies upon a mean flow. The eddies are loosely defined as coherent patterns of flow velocity, vorticity and pressure. Turbulent flows may be viewed as made of an entire hierarchy of eddies over a wide range of length scales and the hierarchy can be described by the energy spectrum that measures the energy in flow velocity fluctuations for each length scale (wavenumber
In the physical sciences, the wavenumber (also wave number or repetency) is the ''spatial frequency'' of a wave, measured in cycles per unit distance (ordinary wavenumber) or radians per unit distance (angular wavenumber). It is analogous to temp ...
). The scales in the energy cascade are generally uncontrollable and highly non-symmetric. Nevertheless, based on these length scales these eddies can be divided into three categories.
; Integral time scale
The integral time scale for a Lagrangian flow can be defined as:
:
where ''u''′ is the velocity fluctuation, and is the time lag between measurements.
; Integral length scales
: Large eddies obtain energy from the mean flow and also from each other. Thus, these are the energy production eddies which contain most of the energy. They have the large flow velocity fluctuation and are low in frequency. Integral scales are highly anisotropic
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physic ...
and are defined in terms of the normalized two-point flow velocity correlations. The maximum length of these scales is constrained by the characteristic length of the apparatus. For example, the largest integral length scale of pipe flow is equal to the pipe diameter. In the case of atmospheric turbulence, this length can reach up to the order of several hundreds kilometers.: The integral length scale can be defined as
::
: where ''r'' is the distance between two measurement locations, and ''u''′ is the velocity fluctuation in that same direction.
; Kolmogorov length scales : Smallest scales in the spectrum that form the viscous sub-layer range. In this range, the energy input from nonlinear interactions and the energy drain from viscous dissipation are in exact balance. The small scales have high frequency, causing turbulence to be locally isotropic
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe ...
and homogeneous.
; Taylor microscale The Taylor microscale, which is sometimes called the turbulence length scale, is a length scale used to characterize a turbulent fluid flow. This microscale is named after Geoffrey Ingram Taylor. The Taylor microscale is the intermediate length scal ...
s : The intermediate scales between the largest and the smallest scales which make the inertial subrange. Taylor microscales are not dissipative scales, but pass down the energy from the largest to the smallest without dissipation. Some literatures do not consider Taylor microscales as a characteristic length scale and consider the energy cascade to contain only the largest and smallest scales; while the latter accommodate both the inertial subrange and the viscous sublayer. Nevertheless, Taylor microscales are often used in describing the term "turbulence" more conveniently as these Taylor microscales play a dominant role in energy and momentum transfer in the wavenumber space.
Although it is possible to find some particular solutions of the Navier–Stokes equations governing fluid motion, all such solutions are unstable to finite perturbations at large Reynolds numbers. Sensitive dependence on the initial and boundary conditions makes fluid flow irregular both in time and in space so that a statistical description is needed. The Russia
Russia (, , ), or the Russian Federation, is a List of transcontinental countries, transcontinental country spanning Eastern Europe and North Asia, Northern Asia. It is the List of countries and dependencies by area, largest country in the ...
n mathematician Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov ( rus, Андре́й Никола́евич Колмого́ров, p=ɐnˈdrʲej nʲɪkɐˈlajɪvʲɪtɕ kəlmɐˈɡorəf, a=Ru-Andrey Nikolaevich Kolmogorov.ogg, 25 April 1903 – 20 October 1987) was a Sovi ...
proposed the first statistical theory of turbulence, based on the aforementioned notion of the energy cascade (an idea originally introduced by Richardson
Richardson may refer to:
People
* Richardson (surname), an English and Scottish surname
* Richardson Gang, a London crime gang in the 1960s
* Richardson Dilworth, Mayor of Philadelphia (1956-1962)
Places Australia
* Richardson, Australian Cap ...
) and the concept of self-similarity. As a result, the Kolmogorov microscales
In fluid dynamics, Kolmogorov microscales are the smallest scales in the turbulent flow of fluids. At the Kolmogorov scale, viscosity dominates and the turbulence kinetic energy is dissipated into thermal energy. They are defined by
where
* i ...
were named after him. It is now known that the self-similarity is broken so the statistical description is presently modified.
A complete description of turbulence is one of the unsolved problems in physics
The following is a list of notable unsolved problems grouped into broad areas of physics.
Some of the major unsolved problems in physics are theoretical, meaning that existing theories seem incapable of explaining a certain observed phenomenon ...
. According to an apocryphal story, Werner Heisenberg
Werner Karl Heisenberg () (5 December 1901 – 1 February 1976) was a German theoretical physicist and one of the main pioneers of the theory of quantum mechanics. He published his work in 1925 in a breakthrough paper. In the subsequent series ...
was asked what he would ask God, given the opportunity. His reply was: "When I meet God, I am going to ask him two questions: Why relativity? And why turbulence? I really believe he will have an answer for the first." A similar witticism has been attributed to Horace Lamb in a speech to the British Association for the Advancement of Science
The British Science Association (BSA) is a charity and learned society founded in 1831 to aid in the promotion and development of science. Until 2009 it was known as the British Association for the Advancement of Science (BA). The current Chie ...
: "I am an old man now, and when I die and go to heaven there are two matters on which I hope for enlightenment. One is quantum electrodynamics, and the other is the turbulent motion of fluids. And about the former I am rather more optimistic."
Onset of turbulence
 The onset of turbulence can be, to some extent, predicted by the
The onset of turbulence can be, to some extent, predicted by the Reynolds number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be domi ...
, which is the ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
of inertial forces to viscous
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the inter ...
forces within a fluid which is subject to relative internal movement due to different fluid velocities, in what is known as a boundary layer in the case of a bounding surface such as the interior of a pipe. A similar effect is created by the introduction of a stream of higher velocity fluid, such as the hot gases from a flame in air. This relative movement generates fluid friction, which is a factor in developing turbulent flow. Counteracting this effect is the viscosity of the fluid, which as it increases, progressively inhibits turbulence, as more kinetic energy is absorbed by a more viscous fluid. The Reynolds number quantifies the relative importance of these two types of forces for given flow conditions, and is a guide to when turbulent flow will occur in a particular situation.
This ability to predict the onset of turbulent flow is an important design tool for equipment such as piping systems or aircraft wings, but the Reynolds number is also used in scaling of fluid dynamics problems, and is used to determine dynamic similitude
Similitude is a concept applicable to the testing of engineering models. A model is said to have similitude with the real application if the two share geometric similarity, kinematic similarity and dynamic similarity. ''Similarity'' and ''simili ...
between two different cases of fluid flow, such as between a model aircraft, and its full size version. Such scaling is not always linear and the application of Reynolds numbers to both situations allows scaling factors to be developed.
A flow situation in which the kinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its accele ...
is significantly absorbed due to the action of fluid molecular viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the inte ...
gives rise to a laminar flow
In fluid dynamics, laminar flow is characterized by fluid particles following smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mi ...
regime. For this the dimensionless quantity the Reynolds number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be domi ...
() is used as a guide.
With respect to laminar
Laminar means "flat". Laminar may refer to:
Terms in science and engineering:
* Laminar electronics or organic electronics, a branch of material sciences dealing with electrically conductive polymers and small molecules
* Laminar armour or "band ...
and turbulent flow regimes:
* laminar flow occurs at low Reynolds numbers, where viscous forces are dominant, and is characterized by smooth, constant fluid motion;
* turbulent flow occurs at high Reynolds numbers and is dominated by inertial forces, which tend to produce chaotic eddies
In fluid dynamics, an eddy is the swirling of a fluid and the reverse current created when the fluid is in a turbulent flow regime. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object. Fluid beh ...
, vortices
In fluid dynamics, a vortex ( : vortices or vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in th ...
and other flow instabilities.
The Reynolds number is defined as
:
where:
* is the density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
of the fluid (SI units
The International System of Units, known by the international abbreviation SI in all languages and sometimes Pleonasm#Acronyms and initialisms, pleonastically as the SI system, is the modern form of the metric system and the world's most wid ...
: kg/m3)
* is a characteristic velocity of the fluid with respect to the object (m/s)
* is a characteristic linear dimension (m)
* is the dynamic viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the inter ...
of the fluid
In physics, a fluid is a liquid, gas, or other material that continuously deforms (''flows'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot resist any shear ...
(Pa·s or N·s/m2 or kg/(m·s)).
While there is no theorem directly relating the non-dimensional Reynolds number to turbulence, flows at Reynolds numbers larger than 5000 are typically (but not necessarily) turbulent, while those at low Reynolds numbers usually remain laminar. In Poiseuille flow, for example, turbulence can first be sustained if the Reynolds number is larger than a critical value of about 2040; moreover, the turbulence is generally interspersed with laminar flow until a larger Reynolds number of about 4000.
The transition occurs if the size of the object is gradually increased, or the viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the inte ...
of the fluid is decreased, or if the density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
of the fluid is increased.
Heat and momentum transfer
When flow is turbulent, particles exhibit additional transverse motion which enhances the rate of energy and momentum exchange between them thus increasing theheat transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, ...
and the friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative lateral motion of t ...
coefficient.
Assume for a two-dimensional turbulent flow that one was able to locate a specific point in the fluid and measure the actual flow velocity of every particle that passed through that point at any given time. Then one would find the actual flow velocity fluctuating about a mean value:
:
and similarly for temperature () and pressure (), where the primed quantities denote fluctuations superposed to the mean. This decomposition of a flow variable into a mean value and a turbulent fluctuation was originally proposed by Osborne Reynolds in 1895, and is considered to be the beginning of the systematic mathematical analysis of turbulent flow, as a sub-field of fluid dynamics. While the mean values are taken as predictable variables determined by dynamics laws, the turbulent fluctuations are regarded as stochastic variables.
The heat flux and momentum transfer (represented by the shear stress ) in the direction normal to the flow for a given time are
:
where is the heat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity i ...
at constant pressure, is the density of the fluid, is the coefficient of turbulent viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the inte ...
and is the turbulent thermal conductivity
The thermal conductivity of a material is a measure of its ability to conduct heat. It is commonly denoted by k, \lambda, or \kappa.
Heat transfer occurs at a lower rate in materials of low thermal conductivity than in materials of high thermal ...
.
Kolmogorov's theory of 1941
Richardson's notion of turbulence was that a turbulent flow is composed by "eddies" of different sizes. The sizes define a characteristic length scale for the eddies, which are also characterized by flow velocity scales and time scales (turnover time) dependent on the length scale. The large eddies are unstable and eventually break up originating smaller eddies, and the kinetic energy of the initial large eddy is divided into the smaller eddies that stemmed from it. These smaller eddies undergo the same process, giving rise to even smaller eddies which inherit the energy of their predecessor eddy, and so on. In this way, the energy is passed down from the large scales of the motion to smaller scales until reaching a sufficiently small length scale such that the viscosity of the fluid can effectively dissipate the kinetic energy into internal energy. In his original theory of 1941, Kolmogorov postulated that for very highReynolds number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be domi ...
s, the small-scale turbulent motions are statistically isotropic (i.e. no preferential spatial direction could be discerned). In general, the large scales of a flow are not isotropic, since they are determined by the particular geometrical features of the boundaries (the size characterizing the large scales will be denoted as ). Kolmogorov's idea was that in the Richardson's energy cascade this geometrical and directional information is lost, while the scale is reduced, so that the statistics of the small scales has a universal character: they are the same for all turbulent flows when the Reynolds number is sufficiently high.
Thus, Kolmogorov introduced a second hypothesis: for very high Reynolds numbers the statistics of small scales are universally and uniquely determined by the kinematic viscosity and the rate of energy dissipation . With only these two parameters, the unique length that can be formed by dimensional analysis is
:
This is today known as the Kolmogorov length scale (see Kolmogorov microscales
In fluid dynamics, Kolmogorov microscales are the smallest scales in the turbulent flow of fluids. At the Kolmogorov scale, viscosity dominates and the turbulence kinetic energy is dissipated into thermal energy. They are defined by
where
* i ...
).
A turbulent flow is characterized by a hierarchy of scales through which the energy cascade takes place. Dissipation of kinetic energy takes place at scales of the order of Kolmogorov length , while the input of energy into the cascade comes from the decay of the large scales, of order . These two scales at the extremes of the cascade can differ by several orders of magnitude at high Reynolds numbers. In between there is a range of scales (each one with its own characteristic length ) that has formed at the expense of the energy of the large ones. These scales are very large compared with the Kolmogorov length, but still very small compared with the large scale of the flow (i.e. ). Since eddies in this range are much larger than the dissipative eddies that exist at Kolmogorov scales, kinetic energy is essentially not dissipated in this range, and it is merely transferred to smaller scales until viscous effects become important as the order of the Kolmogorov scale is approached. Within this range inertial effects are still much larger than viscous effects, and it is possible to assume that viscosity does not play a role in their internal dynamics (for this reason this range is called "inertial range").
Hence, a third hypothesis of Kolmogorov was that at very high Reynolds number the statistics of scales in the range are universally and uniquely determined by the scale and the rate of energy dissipation .
The way in which the kinetic energy is distributed over the multiplicity of scales is a fundamental characterization of a turbulent flow. For homogeneous turbulence (i.e., statistically invariant under translations of the reference frame) this is usually done by means of the ''energy spectrum function'' , where is the modulus of the wavevector corresponding to some harmonics in a Fourier representation of the flow velocity field :
:
where is the Fourier transform of the flow velocity field. Thus, represents the contribution to the kinetic energy from all the Fourier modes with , and therefore,
:
where is the mean turbulent kinetic energy of the flow. The wavenumber corresponding to length scale is . Therefore, by dimensional analysis, the only possible form for the energy spectrum function according with the third Kolmogorov's hypothesis is
:
where would be a universal constant. This is one of the most famous results of Kolmogorov 1941 theory, and considerable experimental evidence has accumulated that supports it.
Outside of the inertial area, one can find the formula below :
:
In spite of this success, Kolmogorov theory is at present under revision. This theory implicitly assumes that the turbulence is statistically self-similar at different scales. This essentially means that the statistics are scale-invariant and non-intermittent in the inertial range. A usual way of studying turbulent flow velocity fields is by means of flow velocity increments:
:
that is, the difference in flow velocity between points separated by a vector (since the turbulence is assumed isotropic, the flow velocity increment depends only on the modulus of ). Flow velocity increments are useful because they emphasize the effects of scales of the order of the separation when statistics are computed. The statistical scale-invariance without intermittency implies that the scaling of flow velocity increments should occur with a unique scaling exponent , so that when is scaled by a factor ,
:
should have the same statistical distribution as
:
with independent of the scale . From this fact, and other results of Kolmogorov 1941 theory, it follows that the statistical moments of the flow velocity increments (known as ''structure functions'' in turbulence) should scale as
:
where the brackets denote the statistical average, and the would be universal constants.
There is considerable evidence that turbulent flows deviate from this behavior. The scaling exponents deviate from the value predicted by the theory, becoming a non-linear function of the order of the structure function. The universality of the constants have also been questioned. For low orders the discrepancy with the Kolmogorov value is very small, which explain the success of Kolmogorov theory in regards to low order statistical moments. In particular, it can be shown that when the energy spectrum follows a power law
:
with , the second order structure function has also a power law, with the form
:
Since the experimental values obtained for the second order structure function only deviate slightly from the value predicted by Kolmogorov theory, the value for is very near to (differences are about 2%). Thus the "Kolmogorov − spectrum" is generally observed in turbulence. However, for high order structure functions, the difference with the Kolmogorov scaling is significant, and the breakdown of the statistical self-similarity is clear. This behavior, and the lack of universality of the constants, are related with the phenomenon of intermittency
In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics ( Pomeau–Manneville dynamics), or different forms of chaotic dynamics (crisis-induced intermittency).
Pomeau and Mannev ...
in turbulence and can be related to the non-trivial scaling behavior of the dissipation rate averaged over scale . This is an important area of research in this field, and a major goal of the modern theory of turbulence is to understand what is universal in the inertial range, and how to deduce intermittency properties from the Navier-Stokes equations, i.e. from first principles.
See also
* Astronomical seeing * Atmospheric dispersion modeling *Chaos theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have co ...
* Clear-air turbulence
* Different types of boundary conditions in fluid dynamics
Boundary conditions in fluid dynamics are the set of constraints to boundary value problems in computational fluid dynamics. These boundary conditions include inlet boundary conditions, outlet boundary conditions, wall boundary conditions, constan ...
* Eddy covariance
* Fluid dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) an ...
** Darcy–Weisbach equation
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation ...
** Eddy
** Navier–Stokes equations
** Large eddy simulation
Large eddy simulation (LES) is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and first explored by Deardorff (1970). LES is c ...
** Hagen–Poiseuille equation
In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow ...
** Kelvin–Helmholtz instability
** Lagrangian coherent structure
Lagrangian coherent structures (LCSs) are distinguished surfaces of trajectories in a dynamical system that exert a major influence on nearby trajectories over a time interval of interest. The type of this influence may vary, but it invariably cr ...
** Turbulence kinetic energy
* Mesocyclones
* Navier–Stokes existence and smoothness
The Navier–Stokes existence and smoothness problem concerns the mathematical properties of solutions to the Navier–Stokes equations, a system of partial differential equations that describe the motion of a fluid in space. Solutions to the N ...
* Reynolds number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be domi ...
* Swing bowling
* Taylor microscale The Taylor microscale, which is sometimes called the turbulence length scale, is a length scale used to characterize a turbulent fluid flow. This microscale is named after Geoffrey Ingram Taylor. The Taylor microscale is the intermediate length scal ...
* Turbulence modeling
* Velocimetry
Velocimetry is the measurement of the velocity of fluids. This is a task often taken for granted, and involves far more complex processes than one might expect. It is often used to solve fluid dynamics problems, study fluid networks, in industria ...
* Vertical draft
* Vortex
In fluid dynamics, a vortex ( : vortices or vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in th ...
* Vortex generator
* Wake turbulence
Wake turbulence is a disturbance in the atmosphere that forms behind an aircraft as it passes through the air. It includes variety of elements, the most significant of which are wingtip vortices and jetwash. Jetwash refers to the rapidly moving g ...
* Wave turbulence
In continuum mechanics, wave turbulence is a set of nonlinear waves deviated far from thermal equilibrium. Such a state is usually accompanied by dissipation. It is either decaying turbulence or requires an external source of energy to sustain it. ...
* Wingtip vortices
Wingtip vortices are circular patterns of rotating air left behind a wing as it generates lift.Clancy, L.J., ''Aerodynamics'', section 5.14 One wingtip vortex trails from the tip of each wing. Wingtip vortices are sometimes named ''trailing'' ...
* Wind tunnel
Wind tunnels are large tubes with air blowing through them which are used to replicate the interaction between air and an object flying through the air or moving along the ground. Researchers use wind tunnels to learn more about how an aircraft ...
References and notes
Further reading
General
* * * * * * * *Original scientific research papers and classic monographs
* **Translated into English: * **Translated into English: *External links
Center for Turbulence Research
Scientific papers and books on turbulence
Center for Turbulence Research
Stanford University
Stanford University, officially Leland Stanford Junior University, is a private research university in Stanford, California. The campus occupies , among the largest in the United States, and enrolls over 17,000 students. Stanford is consider ...
Scientific American article
Air Turbulence Forecast
international CFD database iCFDdatabase
*
Fluid Mechanics website with movies, Q&A, etc
{{Authority control Concepts in physics Aerodynamics Chaos theory Transport phenomena Fluid dynamics Flow regimes