|
Vortex Stretching
In fluid dynamics, vortex stretching is the lengthening of vortices in three-dimensional fluid flow, associated with a corresponding increase of the component of vorticity in the stretching direction—due to the conservation of angular momentum. Vortex stretching is associated with a particular term in the vorticity equation. For example, vorticity transport in an incompressible inviscid flow is governed by : = \left(\vec \cdot \vec\right) \vec, where ''D/Dt'' is the material derivative. The source term on the right hand side is the vortex stretching term. It amplifies the vorticity \vec when the velocity is diverging in the direction parallel to \vec. A simple example of vortex stretching in a viscous flow is provided by the Burgers vortex. Vortex stretching is at the core of the description of the turbulence energy cascade from the large scales to the small scales in turbulence. In general, in turbulence fluid elements are more lengthened than squeezed, on average. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Studies Of Water Passing Obstacles And Falling
Study or studies may refer to: General * Education **Higher education * Clinical trial * Experiment * Observational study * Research * Study skills, abilities and approaches applied to learning Other * Study (art), a drawing or series of drawings done in preparation for a finished piece * ''Study'' (film), a 2012 film by Paolo Benetazzo * ''Study'' (Flandrin), an 1835/36 painting by Hippolyte Flandrin * Study (room), a room in a home used as an office or library * ''Study'' (soundtrack), a soundtrack album from the 2012 film * The Study, a private all-girls school in Westmount, Quebec, Canada * ''Studies'' (journal), published by the Jesuits in Ireland * Eduard Study (1862–1930), German mathematician * Facebook Study, a market research app See also * Étude An étude (; ) or study is an instrumental musical composition, usually short, designed to provide practice material for perfecting a particular musical skill. The tradition of writing études emerged in the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including '' aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vortex
In fluid dynamics, a vortex ( : vortices or vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil. Vortices are a major component of turbulent flow. The distribution of velocity, vorticity (the curl of the flow velocity), as well as the concept of circulation are used to characterise vortices. In most vortices, the fluid flow velocity is greatest next to its axis and decreases in inverse proportion to the distance from the axis. In the absence of external forces, viscous friction within the fluid tends to organise the flow into a collection of irrotational vortices, possibly superimposed to larger-scale flows, including larger-scale vortices. Once formed, vortices can move, stretch, twist, and interact in complex ways. A moving vortex carrie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vorticity
In continuum mechanics, vorticity is a pseudovector field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point and traveling along with the flow. It is an important quantity in the dynamical theory of fluids and provides a convenient framework for understanding a variety of complex flow phenomena, such as the formation and motion of vortex rings. Mathematically, the vorticity \vec is the curl of the flow velocity \vec: :\vec \equiv \nabla \times \vec\,, where \nabla is the nabla operator. Conceptually, \vec could be determined by marking parts of a continuum in a small neighborhood of the point in question, and watching their ''relative'' displacements as they move along the flow. The vorticity \vec would be twice the mean angular velocity vector of those particles relative to their center of mass, oriented according to the right-hand rule. In a two-dimensiona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Of Angular Momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its momentum vector; the latter is in Newtonian mechanics. Unlike linear momentum, angular momentu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Material Derivative
In continuum mechanics, the material derivative describes the time rate of change of some physical quantity (like heat or momentum) of a material element that is subjected to a space-and-time-dependent macroscopic velocity field. The material derivative can serve as a link between Eulerian and Lagrangian descriptions of continuum deformation. For example, in fluid dynamics, the velocity field is the flow velocity, and the quantity of interest might be the temperature of the fluid. In which case, the material derivative then describes the temperature change of a certain fluid parcel with time, as it flows along its pathline (trajectory). Other names There are many other names for the material derivative, including: *advective derivative *convective derivative *derivative following the motion *hydrodynamic derivative *Lagrangian derivative *particle derivative *substantial derivative *substantive derivative *Stokes derivative *total derivative, although the material derivat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Burgers Vortex
In fluid dynamics, the Burgers vortex or Burgers–Rott vortex is an exact solution to the Navier–Stokes equations governing viscous flow, named after Jan Burgers and Nicholas Rott. The Burgers vortex describes a stationary, self-similar flow. An inward, radial flow, tends to concentrate vorticity in a narrow column around the symmetry axis. At the same time, viscous diffusion tends to spread the vorticity. The stationary Burgers vortex arises when the two effects balance. The Burgers vortex, apart from serving as an illustration of the vortex stretching mechanism, may describe such flows as tornados, where the vorticity is provided by continuous convection-driven vortex stretching. Flow field The flow for the Burgers vortex is described in cylindrical (r,\theta,z) coordinates. Assuming axial symmetry (no \theta-dependence), the flow field associated with the axisymmetric stagnation point flow is considered: :v_r= -\alpha r, :v_z=2\alpha z, :v_\theta=\fracg(r), where \alpha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Cascade
In continuum mechanics, an energy cascade involves the transfer of energy from large scales of motion to the small scales (called a direct energy cascade) or a transfer of energy from the small scales to the large scales (called an inverse energy cascade). This transfer of energy between different scales requires that the dynamics of the system is nonlinear. Strictly speaking, a cascade requires the energy transfer to be local in scale (only between fluctuations of nearly the same size), evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain. This concept plays an important role in the study of well-developed turbulence. It was memorably expressed in this poem by Lewis F. Richardson in the 1920s. Energy cascades are also important for wind waves in the theory of wave turbulence. Consider for instance turbulence generated by the air flow around a tall building: the energy-containing eddies generated by flow separation have sizes of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
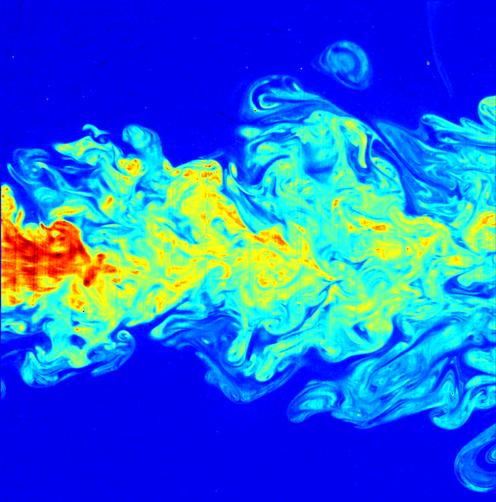
Turbulence
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers. Turbulence is commonly observed in everyday phenomena such as surf, fast flowing rivers, billowing storm clouds, or smoke from a chimney, and most fluid flows occurring in nature or created in engineering applications are turbulent. Turbulence is caused by excessive kinetic energy in parts of a fluid flow, which overcomes the damping effect of the fluid's viscosity. For this reason turbulence is commonly realized in low viscosity fluids. In general terms, in turbulent flow, unsteady vortices appear of many sizes which interact with each other, consequently drag due to friction effects increases. This increases the energy needed to pump fluid through a pipe. The onset of turbulence can be predicted by the dimensionless Rey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Parcel
In fluid dynamics, within the framework of continuum mechanics, a fluid parcel is a very small amount of fluid, identifiable throughout its dynamic history while moving with the fluid flow. As it moves, the mass of a fluid parcel remains constant, while—in a compressible flow—its volume may change. And its shape changes due to the distortion by the flow. In an incompressible flow the volume of the fluid parcel is also a constant ( isochoric flow). This mathematical concept is closely related to the description of fluid motion—its kinematics and dynamics—in a Lagrangian frame of reference. In this reference frame, fluid parcels are labelled and followed through space and time. But also in the Eulerian frame of reference the notion of fluid parcels can be advantageous, for instance in defining the material derivative, streamlines, streaklines, and pathlines; or for determining the Stokes drift. The fluid parcels, as used in continuum mechanics, are to be distinguished ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incompressible Flow
In fluid mechanics or more generally continuum mechanics, incompressible flow ( isochoric flow) refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero (see the derivation below, which illustrates why these conditions are equivalent). Incompressible flow does not imply that the fluid itself is incompressible. It is shown in the derivation below that (under the right conditions) even compressible fluids can – to a good approximation – be modelled as an incompressible flow. Incompressible flow implies that the density remains constant within a parcel of fluid that moves with the flow velocity. Derivation The fundamental requirement for incompressible flow is that the density, \rho , is constant within a small element volume, ''dV'', which moves at the flow velocity u. Mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |