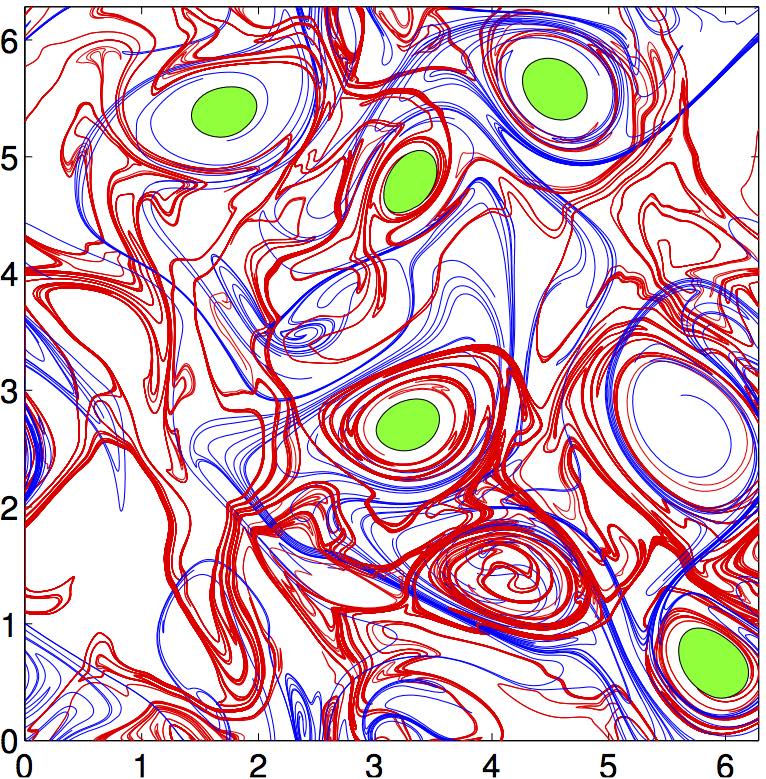
Lagrangian Coherent Structure
Lagrangian coherent structures (LCSs) are distinguished surfaces of trajectories in a dynamical system that exert a major influence on nearby trajectories over a time interval of interest. The type of this influence may vary, but it invariably creates a coherent trajectory pattern for which the underlying LCS serves as a theoretical centerpiece. In observations of tracer patterns in nature, one readily identifies coherent features, but it is often the underlying structure creating these features that is of interest. As illustrated on the right, individual tracer trajectories forming coherent patterns are generally sensitive with respect to changes in their initial conditions and the system parameters. In contrast, the LCSs creating these trajectory patterns turn out to be robust and provide a simplified skeleton of the overall dynamics of the system. The robustness of this skeleton makes LCSs ideal tools for model validation, model comparison and benchmarking. LCSs can also be use ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

LCS Conceptual2
LCS may refer to: Schools and organizations * Laboratory for Computer Science, research institute at the Massachusetts Institute of Technology * Lake County Schools school district of Lake County, Florida * Lakefield College School an independent school in Lakefield, Ontario, Canada * Larchmont Charter School, a public charter school in Los Angeles, California * Lebanese Community School in Lagos, Nigeria * Legal Complaints Service, a former body that formally investigated complaints about solicitors in the United Kingdom * Lincoln Christian College and Seminary * Lincoln Community School in Accra, Ghana * Littlehampton Community School, large secondary school in West Sussex, England * Littleover Community School in Derby, England * Lockerby Composite School Canadian Secondary School in Ontario * London Controlling Section, a British World War II secret organisation * London Co-operative Society, a former consumer co-operative society of the United Kingdom * London Correspondi ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Matrix Similarity
In linear algebra, two ''n''-by-''n'' matrices and are called similar if there exists an invertible ''n''-by-''n'' matrix such that B = P^ A P . Similar matrices represent the same linear map under two (possibly) different bases, with being the change of basis matrix. A transformation is called a similarity transformation or conjugation of the matrix . In the general linear group, similarity is therefore the same as conjugacy, and similar matrices are also called conjugate; however, in a given subgroup of the general linear group, the notion of conjugacy may be more restrictive than similarity, since it requires that be chosen to lie in . Motivating example When defining a linear transformation, it can be the case that a change of basis can result in a simpler form of the same transformation. For example, the matrix representing a rotation in when the axis of rotation is not aligned with the coordinate axis can be complicated to compute. If the axis of rotation were ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Tangent Space
In mathematics, the tangent space of a manifold generalizes to higher dimensions the notion of '' tangent planes'' to surfaces in three dimensions and ''tangent lines'' to curves in two dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold. Informal description In differential geometry, one can attach to every point x of a differentiable manifold a ''tangent space''—a real vector space that intuitively contains the possible directions in which one can tangentially pass through x . The elements of the tangent space at x are called the ''tangent vectors'' at x . This is a generalization of the notion of a vector, based at a given initial point, in a Euclidean space. The dimension of the tangent space at every point of a connected manifold is the same as that of the manifold itself. For example, if the given manifold is a 2 -sphere, then one can picture the ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Nearshore FTLE Of Tidal Interface
Nearshore may refer to: *Littoral zone, the part of a sea, lake or river which is close to the shore *Nearshoring Outsourcing is an agreement in which one company hires another company to be responsible for a planned or existing activity which otherwise is or could be carried out internally, i.e. in-house, and sometimes involves transferring employees and ...

Ridge
A ridge or a mountain ridge is a geographical feature consisting of a chain of mountains or hills that form a continuous elevated crest for an extended distance. The sides of the ridge slope away from the narrow top on either side. The lines along the crest formed by the highest points, with the terrain dropping down on either side, are called the ridgelines. Ridges are usually termed hills or mountains as well, depending on size. Smaller ridges, especially those leaving a larger ridge, are often referred to as spurs. Types There are several main types of ridges: ;Dendritic ridge: In typical dissected plateau terrain, the stream drainage valleys will leave intervening ridges. These are by far the most common ridges. These ridges usually represent slightly more erosion resistant rock, but not always – they often remain because there were more joints where the valleys formed or other chance occurrences. This type of ridge is generally somewhat random in orientation, often ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Skeleton Turbulence
A skeleton is the structural frame that supports the body of an animal. There are several types of skeletons, including the exoskeleton, which is the stable outer shell of an organism, the endoskeleton, which forms the support structure inside the body, and the hydroskeleton, a flexible internal skeleton supported by fluid pressure. Vertebrates are animals with a vertebral column, and their skeletons are typically composed of bone and cartilage. Invertebrates are animals that lack a vertebral column. The skeletons of invertebrates vary, including hard exoskeleton shells, plated endoskeletons, or Sponge spicule, spicules. Cartilage is a rigid connective tissue that is found in the skeletal systems of vertebrates and invertebrates. Etymology The term ''skeleton'' comes . ''Sceleton'' is an archaic form of the word. Classification Skeletons can be defined by several attributes. Solid skeletons consist of hard substances, such as bone, cartilage, or cuticle. These can be further ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Lyapunov Exponent
In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector \delta \mathbf_0 diverge (provided that the divergence can be treated within the linearized approximation) at a rate given by : , \delta\mathbf(t) , \approx e^ , \delta \mathbf_0 , where \lambda is the Lyapunov exponent. The rate of separation can be different for different orientations of initial separation vector. Thus, there is a spectrum of Lyapunov exponents—equal in number to the dimensionality of the phase space. It is common to refer to the largest one as the maximal Lyapunov exponent (MLE), because it determines a notion of predictability for a dynamical system. A positive MLE is usually taken as an indication that the system is chaotic (provided some other conditions are met, e.g., phase space comp ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Finite Strain Theory
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue. Displacement The displacement of a body has two components: a rigid-body displacement and a deformation. * A rigid-body displacement consists of a simultaneous translation (physics) and rotation of the body without changing its shape or size. * Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration \kappa_0(\mathcal B) to a current or deformed configuration \kappa_t(\mathcal B) (Figure 1). A change in the conf ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Normally Hyperbolic Invariant Manifold
A normally hyperbolic invariant manifold (NHIM) is a natural generalization of a hyperbolic fixed point and a hyperbolic set. The difference can be described heuristically as follows: For a manifold \Lambda to be normally hyperbolic we are allowed to assume that the dynamics of \Lambda itself is neutral compared with the dynamics nearby, which is not allowed for a hyperbolic set. NHIMs were introduced by Neil Fenichel in 1972. In this and subsequent papers, Fenichel proves that NHIMs possess stable and unstable manifolds and more importantly, NHIMs and their stable and unstable manifolds persist under small perturbations. Thus, in problems involving perturbation theory, invariant manifolds exist with certain hyperbolicity properties, which can in turn be used to obtain qualitative information about a dynamical system.A. Katok and B. Hasselblatt''Introduction to the Modern Theory of Dynamical Systems'', Cambridge University Press (1996), Definition Let ''M'' be a compact smo ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]