Trig Sub Triangle 3 on:
[Wikipedia]
[Google]
[Amazon]
Trigonometry () is a branch of
 Trigonometric ratios are the ratios between edges of a right triangle. These ratios depend only on one acute angle of the right triangle, since any two right triangles with the same acute angle are similar.
So, these ratios define
Trigonometric ratios are the ratios between edges of a right triangle. These ratios depend only on one acute angle of the right triangle, since any two right triangles with the same acute angle are similar.
So, these ratios define
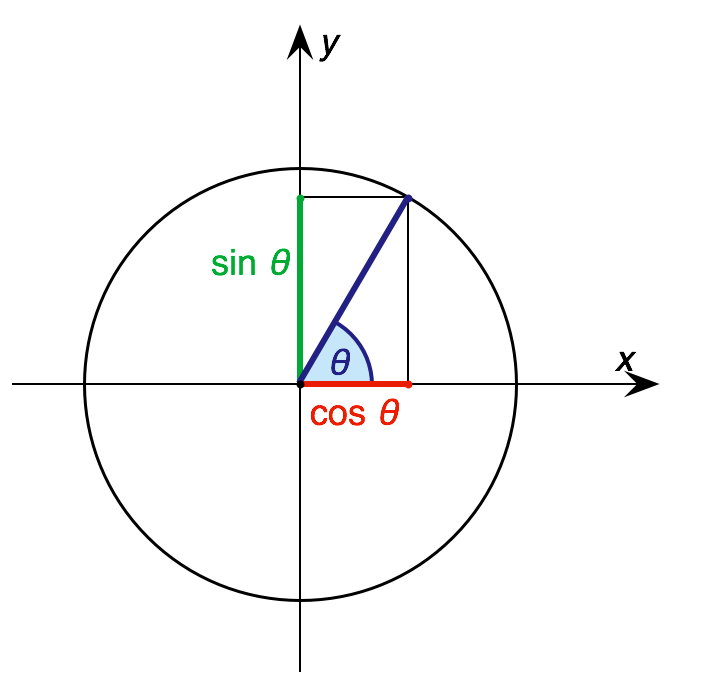
 Trigonometric ratios can also be represented using the
Trigonometric ratios can also be represented using the
 Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the
Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the
 The sine and cosine functions are fundamental to the theory of
The sine and cosine functions are fundamental to the theory of
 Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Extract of page 856
/ref> : : : The second and third equations are derived from dividing the first equation by and , respectively.
Khan Academy: Trigonometry, free online micro lectures
by Alfred Monroe Kenyon and Louis Ingold, The Macmillan Company, 1914. In images, full text presented.
Benjamin Banneker's Trigonometry Puzzle
a
Convergence
Dave's Short Course in Trigonometry
by David Joyce of
Trigonometry, by Michael Corral, Covers elementary trigonometry, Distributed under GNU Free Documentation License
{{Authority control 3rd-century BC introductions
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
concerned with relationships between angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s and side lengths of triangles. In particular, the trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
relate the angles of a right triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees).
The side opposite to the right angle i ...
with ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
s of its side lengths. The field emerged in the Hellenistic world
In classical antiquity, the Hellenistic period covers the time in Greek history after Classical Greece, between the death of Alexander the Great in 323 BC and the death of Cleopatra VII in 30 BC, which was followed by the ascendancy of the Roma ...
during the 3rd century BC from applications of geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
) such as sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite th ...
.
Throughout history, trigonometry has been applied in areas such as geodesy
Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ...
, surveying
Surveying or land surveying is the technique, profession, art, and science of determining the land, terrestrial Plane (mathematics), two-dimensional or Three-dimensional space#In Euclidean geometry, three-dimensional positions of Point (geom ...
, celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, and navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
.
Trigonometry is known for its many identities. These
trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation.
History
Sumer
Sumer () is the earliest known civilization, located in the historical region of southern Mesopotamia (now south-central Iraq), emerging during the Chalcolithic and Early Bronze Age, early Bronze Ages between the sixth and fifth millennium BC. ...
ian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the Babylonians
Babylonia (; , ) was an ancient Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Kuwait, Syria and Iran). It emerged as an Akkadian-populated but Amorite-ru ...
, studied the ratios of the sides of similar triangles and discovered some properties of these ratios but did not turn that into a systematic method for finding sides and angles of triangles. The ancient Nubians used a similar method.
In the 3rd century BC, Hellenistic mathematicians such as Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
and Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
studied the properties of chords
Chord or chords may refer to:
Art and music
* Chord (music), an aggregate of musical pitches sounded simultaneously
** Guitar chord, a chord played on a guitar, which has a particular tuning
* The Chords (British band), 1970s British mod ...
and inscribed angle
In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.
Equivalently, an ...
s in circles, and they proved theorems that are equivalent to modern trigonometric formulae, although they presented them geometrically rather than algebraically. In 140 BC, Hipparchus
Hipparchus (; , ; BC) was a Ancient Greek astronomy, Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equinoxes. Hippar ...
(from Nicaea
Nicaea (also spelled Nicæa or Nicea, ; ), also known as Nikaia (, Attic: , Koine: ), was an ancient Greek city in the north-western Anatolian region of Bithynia. It was the site of the First and Second Councils of Nicaea (the first and seve ...
, Asia Minor) gave the first tables of chords, analogous to modern tables of sine values, and used them to solve problems in trigonometry and spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
. In the 2nd century AD, the Greco-Egyptian astronomer Ptolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
(from Alexandria, Egypt) constructed detailed trigonometric tables (Ptolemy's table of chords
The table of chords, created by the Greece, Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's ''Almagest'', a treatise on mathematical astron ...
) in Book 1, chapter 11 of his ''Almagest
The ''Almagest'' ( ) is a 2nd-century Greek mathematics, mathematical and Greek astronomy, astronomical treatise on the apparent motions of the stars and planetary paths, written by Ptolemy, Claudius Ptolemy ( ) in Koine Greek. One of the most i ...
''. Ptolemy used chord length to define his trigonometric functions, a minor difference from the sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite th ...
convention we use today. (The value we call sin(θ) can be found by looking up the chord length for twice the angle of interest (2θ) in Ptolemy's table, and then dividing that value by two.) Centuries passed before more detailed tables were produced, and Ptolemy's treatise remained in use for performing trigonometric calculations in astronomy throughout the next 1200 years in the medieval Byzantine
The Byzantine Empire, also known as the Eastern Roman Empire, was the continuation of the Roman Empire centred on Constantinople during late antiquity and the Middle Ages. Having survived the events that caused the fall of the Western Roman E ...
, Islamic
Islam is an Abrahamic religions, Abrahamic monotheistic religion based on the Quran, and the teachings of Muhammad. Adherents of Islam are called Muslims, who are estimated to number Islam by country, 2 billion worldwide and are the world ...
, and, later, Western European worlds.
The modern definition of the sine is first attested in the ''Surya Siddhanta
The ''Surya Siddhanta'' (; ) is a Sanskrit treatise in Indian astronomy dated to 4th to 5th century,Menso Folkerts, Craig G. Fraser, Jeremy John Gray, John L. Berggren, Wilbur R. Knorr (2017)Mathematics Encyclopaedia Britannica, Quote: "(...) i ...
'', and its properties were further documented in the 5th century (AD) by Indian mathematician
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta, ...
and astronomer Aryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was the first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy. His works include the '' Āryabhaṭīya'' (which mentions that in 3600 ' ...
. These Greek and Indian works were translated and expanded by medieval Islamic mathematicians. In 830 AD, Persian mathematician Habash al-Hasib al-Marwazi
Ahmad ibn 'Abdallah al-Marwazi, known as Habash al-Hasib (, died 869) was a Persian astronomer, geographer, and mathematician from Merv in Khorasan, who discovered the trigonometric ratios tangent, and cotangent. Al-Biruni who cited Habash in ...
produced the first table of cotangents. By the 10th century AD, in the work of Persian mathematician Abū al-Wafā' al-Būzjānī
Abū al-Wafāʾ Muḥammad ibn Muḥammad ibn Yaḥyā ibn Ismāʿīl ibn al-ʿAbbās al-Būzjānī or Abū al-Wafā Būzhjānī (, ; 10 June 940 – 15 July 998) was a Persian mathematician and astronomer who worked in Baghdad. He made import ...
, all six trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
were used. Abu al-Wafa had sine tables in 0.25° increments, to 8 decimal places of accuracy, and accurate tables of tangent values. He also made important innovations in spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
The Persian
Persian may refer to:
* People and things from Iran, historically called ''Persia'' in the English language
** Persians, the majority ethnic group in Iran, not to be conflated with the Iranic peoples
** Persian language, an Iranian language of the ...
polymath
A polymath or polyhistor is an individual whose knowledge spans many different subjects, known to draw on complex bodies of knowledge to solve specific problems. Polymaths often prefer a specific context in which to explain their knowledge, ...
Nasir al-Din al-Tusi
Muḥammad ibn Muḥammad ibn al-Ḥasan al-Ṭūsī (1201 – 1274), also known as Naṣīr al-Dīn al-Ṭūsī (; ) or simply as (al-)Tusi, was a Persians, Persian polymath, architect, Early Islamic philosophy, philosopher, Islamic medicine, phy ...
has been described as the creator of trigonometry as a mathematical discipline in its own right. He was the first to treat trigonometry as a mathematical discipline independent from astronomy, and he developed spherical trigonometry into its present form. He listed the six distinct cases of a right-angled triangle in spherical trigonometry, and in his ''On the Sector Figure'', he stated the law of sines for plane and spherical triangles, discovered the law of tangents
In trigonometry, the law of tangents or tangent rule is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.
In Figure 1, , , and are the lengths of the three sides of the tr ...
for spherical triangles, and provided proofs for both these laws. Knowledge of trigonometric functions and methods reached Western Europe
Western Europe is the western region of Europe. The region's extent varies depending on context.
The concept of "the West" appeared in Europe in juxtaposition to "the East" and originally applied to the Western half of the ancient Mediterranean ...
via Latin translations of Ptolemy's Greek ''Almagest'' as well as the works of Persian and Arab astronomers such as Al Battani and Nasir al-Din al-Tusi
Muḥammad ibn Muḥammad ibn al-Ḥasan al-Ṭūsī (1201 – 1274), also known as Naṣīr al-Dīn al-Ṭūsī (; ) or simply as (al-)Tusi, was a Persians, Persian polymath, architect, Early Islamic philosophy, philosopher, Islamic medicine, phy ...
. One of the earliest works on trigonometry by a northern European mathematician is ''De Triangulis'' by the 15th century German mathematician Regiomontanus
Johannes Müller von Königsberg (6 June 1436 – 6 July 1476), better known as Regiomontanus (), was a mathematician, astrologer and astronomer of the German Renaissance, active in Vienna, Buda and Nuremberg. His contributions were instrument ...
, who was encouraged to write, and provided with a copy of the ''Almagest'', by the Byzantine Greek scholar cardinal Basilios Bessarion
Bessarion (; 2 January 1403 – 18 November 1472) was a Byzantine Greeks, Byzantine Greek Renaissance humanist, theologian, Catholic Church, Catholic Cardinal (Catholic Church), cardinal and one of the famed Greek scholars who contributed ...
with whom he lived for several years. At the same time, another translation of the ''Almagest'' from Greek into Latin was completed by the Cretan George of Trebizond
George of Trebizond (; 1395–1486) was a Byzantine Greek philosopher, scholar, and humanist.
Life
He was born on the Greek island of Crete (then a Venetian colony known as the Kingdom of Candia), and derived his surname Trapezuntius (Τραπ ...
. Trigonometry was still so little known in 16th-century northern Europe that Nicolaus Copernicus
Nicolaus Copernicus (19 February 1473 – 24 May 1543) was a Renaissance polymath who formulated a mathematical model, model of Celestial spheres#Renaissance, the universe that placed heliocentrism, the Sun rather than Earth at its cen ...
devoted two chapters of ''De revolutionibus orbium coelestium
''De revolutionibus orbium coelestium'' (English translation: ''On the Revolutions of the Heavenly Spheres'') is the seminal work on the heliocentric theory of the astronomer Nicolaus Copernicus (1473–1543) of the Polish Renaissance. The book ...
'' to explain its basic concepts.
Driven by the demands of navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
and the growing need for accurate maps of large geographic areas, trigonometry grew into a major branch of mathematics. Bartholomaeus Pitiscus
Bartholomaeus Pitiscus (also ''Barthélemy'' or ''Bartholomeo''; August 24, 1561 – August 24, 1613) was a 16th-century German trigonometrist, astronomer and theologian who first coined the word ''trigonometry''.
Biography
Pitiscus was bor ...
was the first to use the word, publishing his ''Trigonometria'' in 1595. Gemma Frisius
Gemma Frisius (; born Jemme Reinerszoon; December 9, 1508 – May 25, 1555) was a Dutch physician, mathematician, cartographer, philosopher, and instrument maker. He created important globes, improved the mathematical instruments of his day ...
described for the first time the method of triangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to the point from known points.
Applications
In surveying
Specifically in surveying, triangulation involves only angle m ...
still used today in surveying. It was Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
who fully incorporated complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s into trigonometry. The works of the Scottish mathematicians James Gregory in the 17th century and Colin Maclaurin
Colin Maclaurin (; ; February 1698 – 14 June 1746) was a Scottish mathematician who made important contributions to geometry and algebra. He is also known for being a child prodigy and holding the record for being the youngest professor. ...
in the 18th century were influential in the development of trigonometric series
In mathematics, trigonometric series are a special class of orthogonal series of the form
: A_0 + \sum_^\infty A_n \cos + B_n \sin,
where x is the variable and \ and \ are coefficients. It is an infinite version of a trigonometric polynom ...
. Also in the 18th century, Brook Taylor
Brook Taylor (18 August 1685 – 29 December 1731) was an English mathematician and barrister best known for several results in mathematical analysis. Taylor's most famous developments are Taylor's theorem and the Taylor series, essent ...
defined the general Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
.
Trigonometric ratios
function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-orie ...
s of this angle that are called trigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
s. Explicitly, they are defined below as functions of the known angle ''A'', where ''a'', '' b'' and ''h'' refer to the lengths of the sides in the accompanying figure.
In the following definitions, the hypotenuse
In geometry, a hypotenuse is the side of a right triangle opposite to the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called '' catheti'' or ''legs''. Every rectangle can be divided ...
is the side opposite to the 90-degree angle in a right triangle; it is the longest side of the triangle and one of the two sides adjacent to angle ''A''. The adjacent leg is the other side that is adjacent to angle ''A''. The opposite side is the side that is opposite to angle ''A''. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. See below under Mnemonics
A mnemonic device ( ), memory trick or memory device is any learning technique that aids information retention or retrieval in the human memory, often by associating the information with something that is easier to remember.
It makes use of e ...
.
* Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite th ...
(denoted sin), defined as the ratio of the side opposite the angle to the hypotenuse.
::
* Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
(denoted cos), defined as the ratio of the adjacent leg (the side of the triangle joining the angle to the right angle) to the hypotenuse.
::
* Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
(denoted tan), defined as the ratio of the opposite leg to the adjacent leg.
::
The reciprocals of these ratios are named the cosecant (csc), secant (sec), and cotangent (cot), respectively:
:
:
:
The cosine, cotangent, and cosecant are so named because they are respectively the sine, tangent, and secant of the complementary angle abbreviated to "co-".
With these functions, one can answer virtually all questions about arbitrary triangles by using the law of sines
In trigonometry, the law of sines (sometimes called the sine formula or sine rule) is a mathematical equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\ ...
and the law of cosines
In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides , , and , opposite respective angles , , and (see ...
. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and their included angle or two angles and a side or three sides are known.
Mnemonics
A common use ofmnemonic
A mnemonic device ( ), memory trick or memory device is any learning technique that aids information retention or retrieval in the human memory, often by associating the information with something that is easier to remember.
It makes use of e ...
s is to remember facts and relationships in trigonometry. For example, the ''sine'', ''cosine'', and ''tangent'' ratios in a right triangle can be remembered by representing them and their corresponding sides as strings of letters. For instance, a mnemonic is SOH-CAH-TOA:
:Sine = Opposite ÷ Hypotenuse
:Cosine = Adjacent ÷ Hypotenuse
:Tangent = Opposite ÷ Adjacent
One way to remember the letters is to sound them out phonetically (i.e. , similar to Krakatoa
Krakatoa (), also transcribed (), is a caldera in the Sunda Strait between the islands of Java and Sumatra in the Indonesian province of Lampung. The caldera is part of a volcanic island group (Krakatoa archipelago) comprising four islands. Tw ...
). Another method is to expand the letters into a sentence, such as "Some Old Hippie Caught Another Hippie Trippin' On Acid".
The unit circle and common trigonometric values

unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, which is the circle of radius 1 centered at the origin in the plane. In this setting, the terminal side of an angle ''A'' placed in standard position will intersect the unit circle in a point (x,y), where and . This representation allows for the calculation of commonly found trigonometric values, such as those in the following table:
Trigonometric functions of real or complex variables
Using theunit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, one can extend the definitions of trigonometric ratios to all positive and negative arguments (see trigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
).
Graphs of trigonometric functions
The following table summarizes the properties of the graphs of the six main trigonometric functions:Inverse trigonometric functions
Because the six main trigonometric functions are periodic, they are notinjective
In mathematics, an injective function (also known as injection, or one-to-one function ) is a function that maps distinct elements of its domain to distinct elements of its codomain; that is, implies (equivalently by contraposition, impl ...
(or, 1 to 1), and thus are not invertible. By restricting the domain of a trigonometric function, however, they can be made invertible.
The names of the inverse trigonometric functions, together with their domains and range, can be found in the following table:
Power series representations
When considered as functions of a real variable, the trigonometric ratios can be represented by aninfinite series
In mathematics, a series is, roughly speaking, an addition of infinitely many terms, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathemati ...
. For instance, sine and cosine have the following representations:
:
:
With these definitions the trigonometric functions can be defined for complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s. When extended as functions of real or complex variables, the following formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...
holds for the complex exponential:
:
This complex exponential function, written in terms of trigonometric functions, is particularly useful.
Calculating trigonometric functions
Trigonometric functions were among the earliest uses formathematical table
Mathematical tables are lists of numbers showing the results of a calculation with varying arguments. Trigonometric tables were used in ancient Greece and India for applications to astronomy and celestial navigation, and continued to be widely u ...
s. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate
In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points.
In engineering and science, one often has a ...
between the values listed to get higher accuracy. Slide rule
A slide rule is a hand-operated mechanical calculator consisting of slidable rulers for conducting mathematical operations such as multiplication, division, exponents, roots, logarithms, and trigonometry. It is one of the simplest analog ...
s had special scales for trigonometric functions.
Scientific calculator
A scientific calculator is an Electronics, electronic calculator, either desktop or handheld, designed to perform calculations using basic (addition, subtraction, multiplication, Division (mathematics), division) and advanced (Trigonometric fun ...
s have buttons for calculating the main trigonometric functions (sin, cos, tan, and sometimes cis and their inverses). Most allow a choice of angle measurement methods: degrees, radians, and sometimes gradians
In trigonometry, the gradianalso known as the gon (), grad, or gradeis a unit of measurement of an angle, defined as one-hundredth of the right angle; in other words, 100 gradians is equal to 90 degrees. It is equivalent to of a turn, of a ...
. Most computer programming language
A programming language is a system of notation for writing computer programs.
Programming languages are described in terms of their Syntax (programming languages), syntax (form) and semantics (computer science), semantics (meaning), usually def ...
s provide function libraries that include the trigonometric functions. The floating point unit
A floating-point unit (FPU), numeric processing unit (NPU), colloquially math coprocessor, is a part of a computer system specially designed to carry out operations on floating-point numbers. Typical operations are addition, subtraction, multipli ...
hardware incorporated into the microprocessor chips used in most personal computers has built-in instructions for calculating trigonometric functions.
Other trigonometric functions
In addition to the six ratios listed earlier, there are additional trigonometric functions that were historically important, though seldom used today. These include the chord (), theversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',coversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',haversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',exsecant
The external secant function (abbreviated exsecant, symbolized exsec) is a trigonometric function defined in terms of the secant function:
\operatorname \theta = \sec\theta - 1 = \frac - 1.
It was introduced in 1855 by American civil engineer ...
(), and the excosecant (). See List of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
for more relations between these functions.
Applications
Astronomy
For centuries, spherical trigonometry has been used for locating solar, lunar, and stellar positions, predicting eclipses, and describing the orbits of the planets. In modern times, the technique oftriangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to the point from known points.
Applications
In surveying
Specifically in surveying, triangulation involves only angle m ...
is used in astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
to measure the distance to nearby stars, as well as in satellite navigation system
A satellite or an artificial satellite is an object, typically a spacecraft, placed into orbit around a celestial body. They have a variety of uses, including communication relay, weather forecasting, navigation ( GPS), broadcasting, scientif ...
s.
Navigation
 Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the
Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the Global Positioning System
The Global Positioning System (GPS) is a satellite-based hyperbolic navigation system owned by the United States Space Force and operated by Mission Delta 31. It is one of the global navigation satellite systems (GNSS) that provide ge ...
and artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
for autonomous vehicle
Vehicular automation is using technology to assist or replace the operator of a vehicle such as a car, truck, aircraft, rocket, military vehicle, or boat. Assisted vehicles are ''semi-autonomous'', whereas vehicles that can travel without a ...
s.
Surveying
In landsurveying
Surveying or land surveying is the technique, profession, art, and science of determining the land, terrestrial Plane (mathematics), two-dimensional or Three-dimensional space#In Euclidean geometry, three-dimensional positions of Point (geom ...
, trigonometry is used in the calculation of lengths, areas, and relative angles between objects.
On a larger scale, trigonometry is used in geography
Geography (from Ancient Greek ; combining 'Earth' and 'write', literally 'Earth writing') is the study of the lands, features, inhabitants, and phenomena of Earth. Geography is an all-encompassing discipline that seeks an understanding o ...
to measure distances between landmarks.
Periodic functions
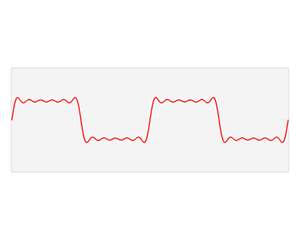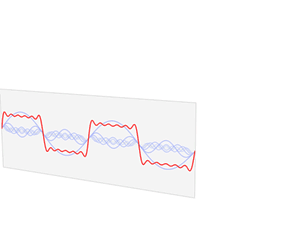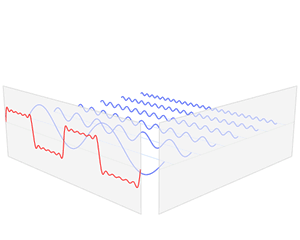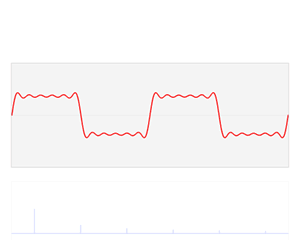
 The sine and cosine functions are fundamental to the theory of
The sine and cosine functions are fundamental to the theory of periodic function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the t ...
s, such as those that describe sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
and light
Light, visible light, or visible radiation is electromagnetic radiation that can be visual perception, perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400– ...
waves. Fourier discovered that every continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
, periodic function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the t ...
could be described as an infinite sum
In mathematics, a series is, roughly speaking, an addition of infinitely many terms, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathemati ...
of trigonometric functions.
Even non-periodic functions can be represented as an integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
of sines and cosines through the Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
. This has applications to quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
and communication
Communication is commonly defined as the transmission of information. Its precise definition is disputed and there are disagreements about whether Intention, unintentional or failed transmissions are included and whether communication not onl ...
s, among other fields.
Optics and acoustics
Trigonometry is useful in manyphysical science
Physical science is a branch of natural science that studies non-living systems, in contrast to life science. It in turn has many branches, each referred to as a "physical science", together is called the "physical sciences".
Definition
...
s, including acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
, and optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
. In these areas, they are used to describe sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
and light wave
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength, ra ...
s, and to solve boundary- and transmission-related problems.
Other applications
Other fields that use trigonometry or trigonometric functions includemusic theory
Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, ...
, geodesy
Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ...
, audio synthesis, architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and construction, constructi ...
, electronics
Electronics is a scientific and engineering discipline that studies and applies the principles of physics to design, create, and operate devices that manipulate electrons and other Electric charge, electrically charged particles. It is a subfield ...
, biology
Biology is the scientific study of life and living organisms. It is a broad natural science that encompasses a wide range of fields and unifying principles that explain the structure, function, growth, History of life, origin, evolution, and ...
, medical imaging
Medical imaging is the technique and process of imaging the interior of a body for clinical analysis and medical intervention, as well as visual representation of the function of some organs or tissues (physiology). Medical imaging seeks to revea ...
(CT scan
A computed tomography scan (CT scan), formerly called computed axial tomography scan (CAT scan), is a medical imaging technique used to obtain detailed internal images of the body. The personnel that perform CT scans are called radiographers or ...
s and ultrasound
Ultrasound is sound with frequency, frequencies greater than 20 Hertz, kilohertz. This frequency is the approximate upper audible hearing range, limit of human hearing in healthy young adults. The physical principles of acoustic waves apply ...
), chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
, number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
(and hence cryptology
Cryptography, or cryptology (from "hidden, secret"; and ''graphein'', "to write", or ''-logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of adversarial behavior. More gener ...
), seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic ...
, meteorology
Meteorology is the scientific study of the Earth's atmosphere and short-term atmospheric phenomena (i.e. weather), with a focus on weather forecasting. It has applications in the military, aviation, energy production, transport, agricultur ...
, oceanography
Oceanography (), also known as oceanology, sea science, ocean science, and marine science, is the scientific study of the ocean, including its physics, chemistry, biology, and geology.
It is an Earth science, which covers a wide range of to ...
, image compression
Image compression is a type of data compression applied to digital images, to reduce their cost for computer data storage, storage or data transmission, transmission. Algorithms may take advantage of visual perception and the statistical properti ...
, phonetics
Phonetics is a branch of linguistics that studies how humans produce and perceive sounds or, in the case of sign languages, the equivalent aspects of sign. Linguists who specialize in studying the physical properties of speech are phoneticians ...
, economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
, electrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, mechanical engineering
Mechanical engineering is the study of physical machines and mechanism (engineering), mechanisms that may involve force and movement. It is an engineering branch that combines engineering physics and engineering mathematics, mathematics principl ...
, civil engineering
Civil engineering is a regulation and licensure in engineering, professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including public works such as roads ...
, computer graphics
Computer graphics deals with generating images and art with the aid of computers. Computer graphics is a core technology in digital photography, film, video games, digital art, cell phone and computer displays, and many specialized applications. ...
, cartography
Cartography (; from , 'papyrus, sheet of paper, map'; and , 'write') is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can ...
, crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
and game development
game development (sometimes shortened to gamedev) is the process of creating a video game. It is a multidisciplinary practice, involving programming, design, art, audio, user interface, and writing. Each of those may be made up of more specialize ...
.
Identities
 Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Triangle identities
In the following identities, ''A'', ''B'' and ''C'' are the angles of a triangle and ''a'', ''b'' and ''c'' are the lengths of sides of the triangle opposite the respective angles (as shown in the diagram).Law of sines
Thelaw of sines
In trigonometry, the law of sines (sometimes called the sine formula or sine rule) is a mathematical equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\ ...
(also known as the "sine rule") for an arbitrary triangle states:
:
where is the area of the triangle and ''R'' is the radius of the circumscribed circle In geometry, a circumscribed circle for a set of points is a circle passing through each of them. Such a circle is said to ''circumscribe'' the points or a polygon formed from them; such a polygon is said to be ''inscribed'' in the circle.
* Circu ...
of the triangle:
:
Law of cosines
Thelaw of cosines
In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides , , and , opposite respective angles , , and (see ...
(known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:
:
or equivalently:
:
Law of tangents
Thelaw of tangents
In trigonometry, the law of tangents or tangent rule is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.
In Figure 1, , , and are the lengths of the three sides of the tr ...
, developed by François Viète
François Viète (; 1540 – 23 February 1603), known in Latin as Franciscus Vieta, was a French people, French mathematician whose work on new algebra was an important step towards modern algebra, due to his innovative use of letters as par ...
, is an alternative to the Law of Cosines when solving for the unknown edges of a triangle, providing simpler computations when using trigonometric tables. It is given by:
:
Area
Given two sides ''a'' and ''b'' and the angle between the sides ''C'', the area of the triangle is given by half the product of the lengths of two sides and the sine of the angle between the two sides: :Trigonometric identities
Pythagorean identities
The following trigonometric identities are related to thePythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
and hold for any value:/ref> : : : The second and third equations are derived from dividing the first equation by and , respectively.
Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for ...
, which states that , produces the following analytical identities for sine, cosine, and tangent in terms of '' e'' and the imaginary unit
The imaginary unit or unit imaginary number () is a mathematical constant that is a solution to the quadratic equation Although there is no real number with this property, can be used to extend the real numbers to what are called complex num ...
''i'':
:
Other trigonometric identities
Other commonly used trigonometric identities include the half-angle identities, the angle sum and difference identities, and the product-to-sum identities.See also
* Aryabhata's sine table * Generalized trigonometry *Lénárt sphere
A Lénárt sphere is an educational manipulative and writing surface for exploring spherical geometry, invented by Hungarian István Lénárt as a modern replacement for a spherical blackboard. It can be used for visualizing the geometry of poi ...
* List of triangle topics
* List of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
* Rational trigonometry
* Skinny triangle
In trigonometry, a skinny triangle is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to that angle in radians. The ...
* Small-angle approximation
For small angles, the trigonometric functions sine, cosine, and tangent can be calculated with reasonable accuracy by the following simple approximations:
:
\begin
\sin \theta &\approx \tan \theta \approx \theta, \\ mu\cos \theta &\approx 1 - \t ...
* Trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
* Unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
* Uses of trigonometry
References
Bibliography
* * *Further reading
* * Linton, Christopher M. (2004). ''From Eudoxus to Einstein: A History of Mathematical Astronomy''. Cambridge University Press. *External links
Khan Academy: Trigonometry, free online micro lectures
by Alfred Monroe Kenyon and Louis Ingold, The Macmillan Company, 1914. In images, full text presented.
Benjamin Banneker's Trigonometry Puzzle
a
Convergence
Dave's Short Course in Trigonometry
by David Joyce of
Clark University
Clark University is a private research university in Worcester, Massachusetts, United States. Founded in 1887 with a large endowment from its namesake Jonas Gilman Clark, a prominent businessman, Clark was one of the first modern research uni ...
Trigonometry, by Michael Corral, Covers elementary trigonometry, Distributed under GNU Free Documentation License
{{Authority control 3rd-century BC introductions