|
Hypotenuse
In geometry, a hypotenuse is the side of a right triangle opposite to the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called '' catheti'' or ''legs''. Every rectangle can be divided into a pair of right triangles by cutting it along either diagonal; the diagonals are the hypotenuses of these triangles. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two legs. Mathematically, this can be written as a^2 + b^2 = c^2, where ''a'' is the length of one leg, ''b'' is the length of another leg, and ''c'' is the length of the hypotenuse. For example, if one of the legs of a right angle has a length of 3 and the other has a length of 4, then their squares add up to 25 = 9 + 16 = 3 × 3 + 4 × 4. Since 25 is the square of the hypotenuse, the length of the hypotenuse is the square r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides , and the hypotenuse , sometimes called the Pythagorean equation: :a^2 + b^2 = c^2 . The theorem is named for the Ancient Greece, Greek philosopher Pythagoras, born around 570 BC. The theorem has been Mathematical proof, proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both Geometry, geometric proofs and Algebra, algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypotenuse
In geometry, a hypotenuse is the side of a right triangle opposite to the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called '' catheti'' or ''legs''. Every rectangle can be divided into a pair of right triangles by cutting it along either diagonal; the diagonals are the hypotenuses of these triangles. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two legs. Mathematically, this can be written as a^2 + b^2 = c^2, where ''a'' is the length of one leg, ''b'' is the length of another leg, and ''c'' is the length of the hypotenuse. For example, if one of the legs of a right angle has a length of 3 and the other has a length of 4, then their squares add up to 25 = 9 + 16 = 3 × 3 + 4 × 4. Since 25 is the square of the hypotenuse, the length of the hypotenuse is the square r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
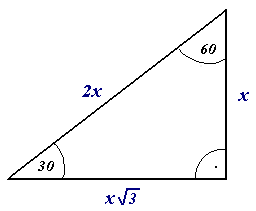
Right Triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees). The side opposite to the right angle is called the '' hypotenuse'' (side c in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: '' cathetus''). Side a may be identified as the side ''adjacent'' to angle B and ''opposite'' (or ''opposed to'') angle A, while side b is the side adjacent to angle A and opposite angle B. Every right triangle is half of a rectangle which has been divided along its diagonal. When the rectangle is a square, its right-triangular half is isosceles, with two congruent sides and two congruent angles. When the rectangle is not a square, its right-triangular half is scalene. Every triangle whose base is the diameter of a circle and whose apex lies on the circle is a right triangle, with the right angle at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real number, real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as Series (mathematics), infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic function, periodic pheno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catheti
In a right triangle, a cathetus (originally from Greek , "perpendicular"; plural: catheti), commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called a "side about the right angle". The side opposite the right angle is the hypotenuse. In the context of the hypotenuse, the catheti are sometimes referred to simply as "the other two sides". If the catheti of a right triangle have equal lengths, the triangle is isosceles. If they have different lengths, a distinction can be made between the minor (shorter) and major (longer) cathetus. The ratio of the lengths of the catheti defines the trigonometric functions tangent and cotangent of the acute angles in the triangle: the ratio c_1/c_2 is the tangent of the acute angle adjacent to c_2 and is also the cotangent of the acute angle adjacent to c_1. In a right triangle, the length of a cathetus is the geometric mean of the length of the adjacent segment cut by the altitude to the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Addition
In mathematics, Pythagorean addition is a binary operation on the real numbers that computes the length of the hypotenuse of a right triangle, given its two sides. Like the more familiar addition and multiplication operations of arithmetic, it is both associative and commutative. This operation can be used in the conversion of Cartesian coordinates to polar coordinates, and in the calculation of Euclidean distance. It also provides a simple notation and terminology for the diameter of a cuboid, the energy-momentum relation in physics, and the overall noise from independent sources of noise. In its applications to signal processing and propagation of measurement uncertainty, the same operation is also called addition in quadrature. A scaled version of this operation gives the quadratic mean or ''root mean square''. It is implemented in many programming libraries as the hypot function, in a way designed to avoid errors arising due to limited-precision calculations performed o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4^2 = (-4)^2 = 16. Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'' or simply ''the square root'' (with a definite article, see below), which is denoted by \sqrt, where the symbol "\sqrt" is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative , the principal square root can also be written in exponent notation, as x^. Every positive number has two square roots: \sqrt (which is positive) and -\sqrt (which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Cosines
In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides , , and , opposite respective angles , , and (see Fig. 1), the law of cosines states: \begin c^2 &= a^2 + b^2 - 2ab\cos\gamma, \\[3mu] a^2 &= b^2+c^2-2bc\cos\alpha, \\[3mu] b^2 &= a^2+c^2-2ac\cos\beta. \end The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if is a right angle then , and the law of cosines special case, reduces to . The law of cosines is useful for solution of triangles, solving a triangle when all three sides or two sides and their included angle are given. Use in solving triangles The theorem is used in solution of triangles, i.e., to find (see Figure 3): *the third side of a triangle if two sides and the angle between them is known: c = \sqrt\,; *the angles of a triangle if the three sides are known: \gamma = \arccos\l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangular Cuboid
A rectangular cuboid is a special case of a cuboid with rectangular faces in which all of its dihedral angles are right angles. This shape is also called rectangular parallelepiped or orthogonal parallelepiped. Many writers just call these "cuboids", without qualifying them as being rectangular, but others use cuboid to refer to a more general class of polyhedra with six quadrilateral faces. Properties A rectangular cuboid is a convex polyhedron with six rectangle faces. The dihedral angles of a rectangular cuboid are all right angles, and its opposite faces are congruent. Because of the faces' orthogonality, the rectangular cuboid is classified as convex orthogonal polyhedron. By definition, this makes it a ''right rectangular prism''. Rectangular cuboids may be referred to colloquially as "boxes" (after the physical object). If two opposite faces become square In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangular Coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |