The N-body Problem

In physics, the -body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally.Leimanis and Minorsky: Our interest is with Leimanis, who first discusses some history about the -body problem, especially Ms. Kovalevskaya's 1868–1888 twenty-year complex-variables approach, failure; Section 1: "The Dynamics of Rigid Bodies and Mathematical Exterior Ballistics" (Chapter 1, "The motion of a rigid body about a fixed point (Euler and Poisson equations)"; Chapter 2, "Mathematical Exterior Ballistics"), good precursor background to the -body problem; Section 2: "Celestial Mechanics" (Chapter 1, "The Uniformization of the Three-body Problem (Restricted Three-body Problem)"; Chapter 2, "Capture in the Three-Body Problem"; Chapter 3, "Generalized -body Problem"). Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important -body problem.See references cited for Heggie and Hut. The -body problem in general relativity is considerably more difficult to solve due to additional factors like time and space distortions.

The classical physical problem can be informally stated as the following:

The two-body problem has been completely solved and is discussed below, as well as the famous ''restricted'' three-body problem.

History

Knowing three orbital positions of a planet's orbit – positions obtained by Sir Isaac Newton from astronomer John Flamsteed – Newton was able to produce an equation by straightforward analytical geometry, to predict a planet's motion; i.e., to give its orbital properties: position, orbital diameter, period and orbital velocity. Having done so, he and others soon discovered over the course of a few years, those equations of motion did not predict some orbits correctly or even very well. Newton realized that this was because gravitational interactive forces amongst all the planets were affecting all their orbits.

The above discovery goes right to the heart of the matter as to what exactly the -body problem is physically: as Newton realized, it is not sufficient to just specify the initial position and velocity, or three orbital positions either, to determine a planet's true orbit: ''the gravitational interactive forces have to be known too''. Thus came the awareness and rise of the -body "problem" in the early 17th century. These gravitational attractive forces do conform to Newton's ''laws of motion'' and to his ''law of universal gravitation'', but the many multiple (-body) interactions have historically made any exact solution intractable. Ironically, this conformity led to the wrong approach.

After Newton's time the -body problem historically was not stated correctly ''because it did not include a reference to those gravitational interactive forces''. Newton does not say it directly but implies in his '' Principia'' the -body problem is unsolvable because of those gravitational interactive forces. Newton said in his ''Principia'', paragraph 21:

Newton concluded via his third law of motion that "according to this Law all bodies must attract each other." This last statement, which implies the existence of gravitational interactive forces, is key.

As shown below, the problem also conforms to Jean Le Rond D'Alembert's non-Newtonian first and second Principles and to the nonlinear -body problem algorithm, the latter allowing for a closed form solution for calculating those interactive forces.

The problem of finding the general solution of the -body problem was considered very important and challenging. Indeed, in the late 19th century King Oscar II of Sweden, advised by Gösta Mittag-Leffler, established a prize for anyone who could find the solution to the problem. The announcement was quite specific:

In case the problem could not be solved, any other important contribution to classical mechanics would then be considered to be prizeworthy. The prize was awarded to Poincaré, even though he did not solve the original problem. (The first version of his contribution even contained a serious error.) The version finally printed contained many important ideas which led to the development of chaos theory. The problem as stated originally was finally solved by Karl Fritiof Sundman for and generalized to by L. K. Babadzanjanz and Qiudong Wang.

General formulation

The -body problem considers point masses in an inertial reference frame in three dimensional space moving under the influence of mutual gravitational attraction. Each mass has a position vector . Newton's second law says that mass times acceleration is equal to the sum of the forces on the mass. Newton's law of gravity says that the gravitational force felt on mass by a single mass is given by
$\mathbf_ = \frac \cdot \frac = \frac,$
where is the gravitational constant and is the magnitude of the distance between and ( metric induced by the norm).

Summing over all masses yields the -body equations of motion:
$m_i \frac = \sum_^n \frac = -\frac$
where is the ''self-potential'' energy
$U = -\sum_ \frac.$

Defining the momentum to be , Hamilton's equations of motion for the -body problem become
$\frac = \frac \qquad \frac = -\frac,$
where the Hamiltonian function is
$H = T + U$
and is the kinetic energy
$T = \sum_^n \frac.$

Hamilton's equations show that the -body problem is a system of first-order differential equations, with initial conditions as initial position coordinates and initial momentum values.

Symmetries in the -body problem yield global integrals of motion that simplify the problem. Translational symmetry of the problem results in the center of mass
$\mathbf = \frac$
moving with constant velocity, so that , where is the linear velocity and is the initial position. The constants of motion and represent six integrals of the motion. Rotational symmetry results in the total angular momentum being constant
$\mathbf = \sum_^n \mathbf_i \times \mathbf_i,$
where × is the cross product. The three components of the total angular momentum yield three more constants of the motion. The last general constant of the motion is given by the conservation of energy . Hence, every -body problem has ten integrals of motion.

Because and are homogeneous functions of degree 2 and −1, respectively, the equations of motion have a scaling invariance: if is a solution, then so is for any .Chenciner 2007

The moment of inertia of an -body system is given by
$I = \sum_^n m_i \mathbf_i \cdot \mathbf_i = \sum_^n m_i \left\, \mathbf_i\right\, ^2$
and the ''virial'' is given by . Then the ''Lagrange–Jacobi formula'' states that
$\frac = 2T - U.$

For systems in ''dynamic equilibrium'', the longterm time average of is zero. Then on average the total kinetic energy is half the total potential energy, , which is an example of the virial theorem for gravitational systems. If is the total mass and a characteristic size of the system (for example, the radius containing half the mass of the system), then the critical time for a system to settle down to a dynamic equilibrium isTrenti 2008
$t_\mathrm = \sqrt\frac.$

Special cases

Two-body problem

Any discussion of planetary interactive forces has always started historically with the two-body problem. The purpose of this section is to relate the real complexity in calculating any planetary forces. Note in this Section also, several subjects, such as gravity, barycenter, Kepler's Laws, etc.; and in the following Section too ( Three-body problem) are discussed on other Wikipedia pages. Here though, these subjects are discussed from the perspective of the -body problem.

The two-body problem () was completely solved by Johann Bernoulli (1667–1748) by ''classical'' theory (and not by Newton) by assuming the main point-mass was ''fixed''; this is outlined here.See Bate, Mueller, and White, Chapter 1: "Two-Body Orbital Mechanics", pp 1–49. These authors were from the Department of Astronautics and Computer Science, United States Air Force Academy. Their textbook is not filled with advanced mathematics. Consider then the motion of two bodies, say the Sun and the Earth, with the Sun ''fixed'', then:
$\begin m_1 \mathbf_1 &= \frac(\mathbf_2-\mathbf_1) &&\quad\text \\ m_2 \mathbf_2 &= \frac(\mathbf_1-\mathbf_2) &&\quad\text \end$

The equation describing the motion of mass relative to mass is readily obtained from the differences between these two equations and after canceling common terms gives:
$\mathbf + \frac \mathbf = \mathbf$
Where

* is the vector position of relative to ;
* is the ''Eulerian'' acceleration ;
*.

The equation is the fundamental differential equation for the two-body problem Bernoulli solved in 1734. Notice for this approach forces have to be determined first, then the equation of motion resolved. This differential equation has elliptic, or parabolic or hyperbolic solutions.

It is incorrect to think of (the Sun) as fixed in space when applying Newton's law of universal gravitation, and to do so leads to erroneous results. The fixed point for two isolated gravitationally interacting bodies is their mutual barycenter, and this two-body problem can be solved exactly, such as using Jacobi coordinates relative to the barycenter.

Dr. Clarence Cleminshaw calculated the approximate position of the Solar System's barycenter, a result achieved mainly by combining only the masses of Jupiter and the Sun. ''Science Program'' stated in reference to his work:

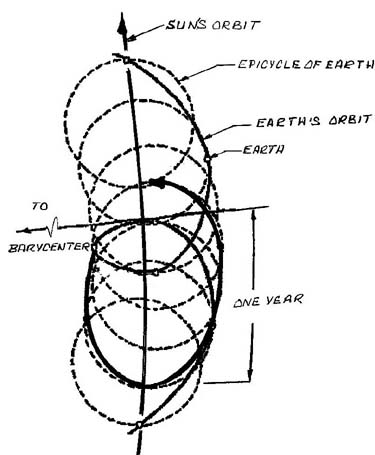
The Sun wobbles as it rotates around the galactic center, dragging the Solar System and Earth along with it. What mathematician Kepler did in arriving at his three famous equations was curve-fit the apparent motions of the planets using Tycho Brahe's data, and ''not'' curve-fitting their true circular motions about the Sun (see Figure). Both Robert Hooke and Newton were well aware that Newton's ''Law of Universal Gravitation'' did not hold for the forces associated with elliptical orbits.See. I. Bernard Cohen's ''Scientific American'' article. In fact, Newton's Universal Law does not account for the orbit of Mercury, the asteroid belt's gravitational behavior, or Saturn's rings. Newton stated (in section 11 of the ''Principia'') that the main reason, however, for failing to predict the forces for elliptical orbits was that his math model was for a body confined to a situation that hardly existed in the real world, namely, the motions of bodies attracted toward an unmoving center. Some present physics and astronomy textbooks do not emphasize the negative significance of Newton's assumption and end up teaching that his mathematical model is in effect reality. It is to be understood that the classical two-body problem solution above is a mathematical idealization. See also Kepler's first law of planetary motion.

Three-body problem

This section relates a historically important -body problem solution after simplifying assumptions were made.

In the past not much was known about the -body problem for . The case has been the most studied. Many earlier attempts to understand the ''Three-body problem'' were quantitative, aiming at finding explicit solutions for special situations.
*In 1687, Isaac Newton published in the ''Principia'' the first steps in the study of the problem of the movements of three bodies subject to their mutual gravitational attractions, but his efforts resulted in verbal descriptions and geometrical sketches; see especially Book 1, Proposition 66 and its corollaries (Newton, 1687 and 1999 (transl.), see also Tisserand, 1894).
*In 1767, Euler found collinear motions, in which three bodies of any masses move proportionately along a fixed straight line. The Euler's three-body problem is the special case in which two of the bodies are fixed in space (this should not be confused with the circular restricted three-body problem, in which the two massive bodies describe a circular orbit and are only fixed in a synodic reference frame).
*In 1772, Lagrange, who published two volumes on the topic, each of 900 pages in length, in 1860 and 1867. Among many other accomplishments, the work already hints at chaos, and clearly demonstrates the problem of so-called "''small denominators''" in perturbation theory.
*In 1917, Forest Ray Moulton published his now classic, ''An Introduction to Celestial Mechanics'' (see references) with its plot of the ''restricted three-body problem'' solution (see figure below). An aside, see Meirovitch's book, pages 413–414 for his restricted three-body problem solution.

Moulton's solution may be easier to visualize (and definitely easier to solve) if one considers the more massive body (such as the Sun) to be stationary in space, and the less massive body (such as Jupiter) to orbit around it, with the equilibrium points (Lagrangian points) maintaining the 60° spacing ahead of, and behind, the less massive body almost in its orbit (although in reality neither of the bodies are truly stationary, as they both orbit the center of mass of the whole system—about the barycenter). For sufficiently small mass ratio of the primaries, these triangular equilibrium points are stable, such that (nearly) massless particles will orbit about these points as they orbit around the larger primary (Sun). The five equilibrium points of the circular problem are known as the Lagrangian points. See figure below:

In the ''restricted three-body problem'' math model figure above (after Moulton), the Lagrangian points L₄ and L₅ are where the Trojan planetoids resided (see Lagrangian point); is the Sun and is Jupiter. L₂ is a point within the asteroid belt. It has to be realized for this model, this whole Sun-Jupiter diagram is rotating about its barycenter. The restricted three-body problem solution predicted the Trojan planetoids before they were first seen. The -circles and closed loops echo the electromagnetic fluxes issued from the Sun and Jupiter. It is conjectured, contrary to Richard H. Batin's conjecture (see References), the two are gravity sinks, in and where gravitational forces are zero, and the reason the Trojan planetoids are trapped there. The total amount of mass of the planetoids is unknown.

The restricted three-body problem that assumes the mass of one of the bodies is negligible. For a discussion of the case where the negligible body is a satellite of the body of lesser mass, see Hill sphere; for binary systems, see Roche lobe. Specific solutions to the three-body problem result in chaotic motion with no obvious sign of a repetitious path.

The restricted problem (both circular and elliptical) was worked on extensively by many famous mathematicians and physicists, most notably by Poincaré at the end of the 19th century. Poincaré's work on the restricted three-body problem was the foundation of deterministic chaos theory. In the restricted problem, there exist five equilibrium points. Three are collinear with the masses (in the rotating frame) and are unstable. The remaining two are located on the third vertex of both equilateral triangles of which the two bodies are the first and second vertices.

Four-body problem

Inspired by the circular restricted three-body problem, the four-body problem can be greatly simplified by considering a smaller body to have a small mass compared to the other three massive bodies, which in turn are approximated to describe circular orbits. This is known as the bicircular restricted four-body problem (also known as bicircular model) and it can be traced back to 1960 in a NASA report written by Su-Shu Huang. This formulation has been highly relevant in the astrodynamics, mainly to model spacecraft trajectories in the Earth-Moon system with the addition of the gravitational attraction of the Sun. The former formulation of the bicircular restricted four-body problem can be problematic when modelling other systems than the Earth-Moon-Sun, so the formulation was generalized by Negri and Prado to expand the application range and improve the accuracy without loss of simplicity.

Planetary problem

The ''planetary problem'' is the -body problem in the case that one of the masses is much larger than all the others. A prototypical example of a planetary problem is the Sun–Jupiter–Saturn system, where the mass of the Sun is about 1000 times larger than the masses of Jupiter or Saturn. An approximate solution to the problem is to decompose it into pairs of star–planet Kepler problems, treating interactions among the planets as perturbations. Perturbative approximation works well as long as there are no orbital resonances in the system, that is none of the ratios of unperturbed Kepler frequencies is a rational number. Resonances appear as small denominators in the expansion.

The existence of resonances and small denominators led to the important question of stability in the planetary problem: do planets, in nearly circular orbits around a star, remain in stable or bounded orbits over time?Chierchia 2010 In 1963, Vladimir Arnold proved using KAM theory a kind of stability of the planetary problem: there exists a set of positive measure of quasiperiodic orbits in the case of the planetary problem restricted to the plane. In the KAM theory, chaotic planetary orbits would be bounded by quasiperiodic KAM tori. Arnold's result was extended to a more general theorem by Féjoz and Herman in 2004.

Central configurations

A central configuration is an initial configuration such that if the particles were all released with zero velocity, they would all collapse toward the center of mass . Such a motion is called ''homothetic''. Central configurations may also give rise to ''homographic motions'' in which all masses moves along Keplerian trajectories (elliptical, circular, parabolic, or hyperbolic), with all trajectories having the same eccentricity . For elliptical trajectories, corresponds to homothetic motion and gives a ''relative equilibrium motion'' in which the configuration remains an isometry of the initial configuration, as if the configuration was a rigid body. Central configurations have played an important role in understanding the topology of invariant manifolds created by fixing the first integrals of a system.

-body choreography

Solutions in which all masses move on the ''same'' curve without collisions are called choreographies. A choreography for was discovered by Lagrange in 1772 in which three bodies are situated at the vertices of an equilateral triangle in the rotating frame. A figure eight choreography for was found numerically by C. Moore in 1993 and generalized and proven by A. Chenciner and R. Montgomery in 2000. Since then, many other choreographies have been found for .

Analytic approaches

For every solution of the problem, not only applying an isometry or a time shift but also a reversal of time (unlike in the case of friction) gives a solution as well.

In the physical literature about the -body problem (), sometimes reference is made to ''the impossibility of solving the -body problem'' (via employing the above approach). However, care must be taken when discussing the 'impossibility' of a solution, as this refers only to the method of first integrals (compare the theorems by Abel and Galois about the impossibility of solving algebraic equations of degree five or higher by means of formulas only involving roots).

Power series solution

One way of solving the classical -body problem is "the -body problem by Taylor series".

We start by defining the system of differential equations:
$\frac=G \sum_^n \frac,$

As and are given as initial conditions, every is known. Differentiating results in which at which is also known, and the Taylor series is constructed iteratively.

A generalized Sundman global solution

In order to generalize Sundman's result for the case (or and ) one has to face two obstacles:

#As has been shown by Siegel, collisions which involve more than two bodies cannot be regularized analytically, hence Sundman's regularization cannot be generalized.
#The structure of singularities is more complicated in this case: other types of singularities may occur (see below).

Lastly, Sundman's result was generalized to the case of bodies by Qiudong Wang in the 1990s. Since the structure of singularities is more complicated, Wang had to leave out completely the questions of singularities. The central point of his approach is to transform, in an appropriate manner, the equations to a new system, such that the interval of existence for the solutions of this new system is .

Singularities of the -body problem

There can be two types of singularities of the -body problem:
*collisions of two or more bodies, but for which (the bodies' positions) remains finite. (In this mathematical sense, a "collision" means that two pointlike bodies have identical positions in space.)
*singularities in which a collision does not occur, but does not remain finite. In this scenario, bodies diverge to infinity in a finite time, while at the same time tending towards zero separation (an imaginary collision occurs "at infinity").

The latter ones are called Painlevé's conjecture (no-collisions singularities). Their existence has been conjectured for by Painlevé (see Painlevé conjecture). Examples of this behavior for have been constructed by Xia and a heuristic model for by Gerver. Donald G. Saari has shown that for 4 or fewer bodies, the set of initial data giving rise to singularities has measure zero.

Simulation

While there are analytic solutions available for the classical (i.e. nonrelativistic) two-body problem and for selected configurations with , in general -body problems must be solved or simulated using numerical methods.

Few bodies

For a small number of bodies, an -body problem can be solved using direct methods, also called particle–particle methods. These methods numerically integrate the differential equations of motion. Numerical integration for this problem can be a challenge for several reasons. First, the gravitational potential is singular; it goes to infinity as the distance between two particles goes to zero. The gravitational potential may be ''softened'' to remove the singularity at small distances:
$U_\varepsilon = \sum_ \frac$
Second, in general for , the -body problem is chaotic, which means that even small errors in integration may grow exponentially in time. Third, a simulation may be over large stretches of model time (e.g. millions of years) and numerical errors accumulate as integration time increases.

There are a number of techniques to reduce errors in numerical integration. Local coordinate systems are used to deal with widely differing scales in some problems, for example an Earth–Moon coordinate system in the context of a solar system simulation. Variational methods and perturbation theory can yield approximate analytic trajectories upon which the numerical integration can be a correction. The use of a symplectic integrator ensures that the simulation obeys Hamilton's equations to a high degree of accuracy and in particular that energy is conserved.

Many bodies

Direct methods using numerical integration require on the order of computations to evaluate the potential energy over all pairs of particles, and thus have a time complexity of . For simulations with many particles, the factor makes large-scale calculations especially time consuming.

A number of approximate methods have been developed that reduce the time complexity relative to direct methods:
* Tree code methods, such as a Barnes–Hut simulation, are spatially-hierarchical methods used when distant particle contributions do not need to be computed to high accuracy. The potential of a distant group of particles is computed using a multipole expansion or other approximation of the potential. This allows for a reduction in complexity to .
* Fast multipole methods take advantage of the fact that the multipole-expanded forces from distant particles are similar for particles close to each other, and uses local expansions of far-field forces to reduce computational effort. It is claimed that this further approximation reduces the complexity to .
* Particle mesh methods divide up simulation space into a three dimensional grid onto which the mass density of the particles is interpolated. Then calculating the potential becomes a matter of solving a Poisson equation on the grid, which can be computed in time using fast Fourier transform or time using multigrid techniques. This can provide fast solutions at the cost of higher error for short-range forces. Adaptive mesh refinement can be used to increase accuracy in regions with large numbers of particles.
* P³M and PM-tree methods are hybrid methods that use the particle mesh approximation for distant particles, but use more accurate methods for close particles (within a few grid intervals). P³M stands for ''particle–particle, particle–mesh'' and uses direct methods with softened potentials at close range. PM-tree methods instead use tree codes at close range. As with particle mesh methods, adaptive meshes can increase computational efficiency.
*Mean field methods approximate the system of particles with a time-dependent Boltzmann equation representing the mass density that is coupled to a self-consistent Poisson equation representing the potential. It is a type of smoothed-particle hydrodynamics approximation suitable for large systems.

Strong gravitation

In astrophysical systems with strong gravitational fields, such as those near the event horizon of a black hole, -body simulations must take into account general relativity; such simulations are the domain of numerical relativity. Numerically simulating the Einstein field equations is extremely challenging and a parameterized post-Newtonian formalism (PPN), such as the Einstein–Infeld–Hoffmann equations, is used if possible. The two-body problem in general relativity is analytically solvable only for the Kepler problem, in which one mass is assumed to be much larger than the other.

Other -body problems

Most work done on the -body problem has been on the gravitational problem. But there exist other systems for which -body mathematics and simulation techniques have proven useful.

In large scale electrostatics problems, such as the simulation of proteins and cellular assemblies in structural biology, the Coulomb potential has the same form as the gravitational potential, except that charges may be positive or negative, leading to repulsive as well as attractive forces. ''Fast Coulomb solvers'' are the electrostatic counterpart to fast multipole method simulators. These are often used with periodic boundary conditions on the region simulated and Ewald summation techniques are used to speed up computations.

In statistics and machine learning, some models have loss functions of a form similar to that of the gravitational potential: a sum of kernel functions over all pairs of objects, where the kernel function depends on the distance between the objects in parameter space. Example problems that fit into this form include all-nearest-neighbors in manifold learning, kernel density estimation, and kernel machines. Alternative optimizations to reduce the time complexity to have been developed, such as ''dual tree'' algorithms, that have applicability to the gravitational -body problem as well.

A technique in Computational fluid dynamics called Vortex Methods sees the vorticity in a fluid domain discretized onto particles which are then advected with the velocity at their centers. Because the fluid velocity and vorticity are related via a Poisson's equation, the velocity can be solved in the same manner as gravitation and electrostatics: as an -body summation over all vorticity-containing particles. The summation uses the Biot-Savart law, with vorticity taking the place of electrical current. In the context of particle-laden turbulent multiphase flows, determining an overall disturbance field generated by all particles is an -body problem. If the particles translating within the flow are much smaller than the flow's Kolmogorov scale, their linear Stokes disturbance fields can be superposed, yielding a system of 3 equations for 3 components of disturbance velocities at the location of particles.

See also

*Celestial mechanics
*Gravitational two-body problem
*Jacobi integral
* Natural units
*Numerical model of the Solar System
* Stability of the Solar System
*Few-body systems
*N-body simulation, a method for numerically obtaining trajectories of bodies in an N-body system.

Notes

References

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* Also English translation of 3rd (1726) edition by I. Bernard Cohen and Anne Whitman (Berkeley, CA, 1999). .
*
*
*
*
*
*
*
*
*
*

Further reading

* Employs energy methods rather than a Newtonian approach.
*
*
*
*
*
*



*
*
*
*
* nbody*.zip is available at https://web.archive.org/web/19990221123102/http://ftp.cica.indiana.edu/: see external links.
*
*
*

External links

Three-Body Problem
at Scholarpedia
More detailed information on the three-body problemRegular Keplerian motions in classical many-body systemsApplet demonstrating chaos in restricted three-body problem


* ttps://web.archive.org/web/20090108060338/http://www.telefonica.net/web2/canrosin/index.htm A java applet to simulate the 3D movement of set of particles under gravitational interactionbr>Javascript Simulation of our Solar System
– with links to the original papers of Euler and Lagrange, and to translations, with discussion



Parallel GPU N-body simulation program with fast stackless particles tree traversal

{{DEFAULTSORT:N-Body Problem
Gravity
Orbits
Classical mechanics
Computational problems
Computational physics