|
Fast Multipole Method
__NOTOC__ The fast multipole method (FMM) is a numerical technique that was developed to speed up the calculation of long-ranged forces in the ''n''-body problem. It does this by expanding the system Green's function using a multipole expansion, which allows one to group sources that lie close together and treat them as if they are a single source. The FMM has also been applied in accelerating the iterative solver in the method of moments (MOM) as applied to computational electromagnetics problems. The FMM was first introduced in this manner by Leslie Greengard and Vladimir Rokhlin Jr. and is based on the multipole expansion of the vector Helmholtz equation. By treating the interactions between far-away basis functions using the FMM, the corresponding matrix elements do not need to be explicitly stored, resulting in a significant reduction in required memory. If the FMM is then applied in a hierarchical manner, it can improve the complexity of matrix-vector products in an iterati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Society For Industrial And Applied Mathematics
Society for Industrial and Applied Mathematics (SIAM) is a professional society dedicated to applied mathematics, computational science, and data science through research, publications, and community. SIAM is the world's largest scientific society devoted to applied mathematics, and roughly two-thirds of its membership resides within the United States. Founded in 1951, the organization began holding annual national meetings in 1954, and now hosts conferences, publishes books and scholarly journals, and engages in advocacy in issues of interest to its membership. Members include engineers, scientists, and mathematicians, both those employed in academia and those working in industry. The society supports educational institutions promoting applied mathematics. SIAM is one of the four member organizations of the Joint Policy Board for Mathematics. Membership Membership is open to both individuals and organizations. By the end of its first full year of operation, SIAM had 130 me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
OpenMP
OpenMP (Open Multi-Processing) is an application programming interface (API) that supports multi-platform shared-memory multiprocessing programming in C, C++, and Fortran, on many platforms, instruction-set architectures and operating systems, including Solaris, AIX, FreeBSD, HP-UX, Linux, macOS, and Windows. It consists of a set of compiler directives, library routines, and environment variables that influence run-time behavior. OpenMP is managed by the nonprofit technology consortium ''OpenMP Architecture Review Board'' (or ''OpenMP ARB''), jointly defined by a broad swath of leading computer hardware and software vendors, including Arm, AMD, IBM, Intel, Cray, HP, Fujitsu, Nvidia, NEC, Red Hat, Texas Instruments, and Oracle Corporation. OpenMP uses a portable, scalable model that gives programmers a simple and flexible interface for developing parallel applications for platforms ranging from the standard desktop computer to the supercomputer. An app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inria
The National Institute for Research in Digital Science and Technology (Inria) () is a French national research institution focusing on computer science and applied mathematics. It was created under the name ''Institut de recherche en informatique et en automatique'' (IRIA) in 1967 at Rocquencourt near Paris, part of Plan Calcul. Its first site was the historical premises of SHAPE (central command of NATO military forces), which is still used as Inria's main headquarters. In 1980, IRIA became INRIA. Since 2011, it has been styled ''Inria''. Inria is a Public Scientific and Technical Research Establishment (EPST) under the double supervision of the French Ministry of National Education, Advanced Instruction and Research and the Ministry of Economy, Finance and Industry. Administrative status Inria has 9 research centers distributed across France (in Bordeaux, Grenoble-Inovallée, Lille, Lyon, Nancy, Paris- Rocquencourt, Rennes, Saclay, and Sophia Antipolis) and one center ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-body Simulation
In physics and astronomy, an ''N''-body simulation is a simulation of a dynamical system of particles, usually under the influence of physical forces, such as gravity (see ''n''-body problem for other applications). ''N''-body simulations are widely used tools in astrophysics, from investigating the dynamics of few-body systems like the Earth-Moon- Sun system to understanding the evolution of the large-scale structure of the universe. In physical cosmology, ''N''-body simulations are used to study processes of non-linear structure formation such as galaxy filaments and galaxy halos from the influence of dark matter. Direct ''N''-body simulations are used to study the dynamical evolution of star clusters. Nature of the particles The 'particles' treated by the simulation may or may not correspond to physical objects which are particulate in nature. For example, an N-body simulation of a star cluster might have a particle per star, so each particle has some physical significa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipole Expansion
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on \R^3, or less often on \R^n for some other Multipole expansions are used frequently in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space. The multipole expansion is expressed as a sum of terms with progressively finer angula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barnes–Hut Simulation
The Barnes–Hut simulation (named after Josh Barnes and Piet Hut) is an approximation algorithm for performing an ''n''-body simulation. It is notable for having order O(''n'' log ''n'') compared to a direct-sum algorithm which would be O(''n''2). The simulation volume is usually divided up into cubic cells via an octree (in a three-dimensional space), so that only particles from nearby cells need to be treated individually, and particles in distant cells can be treated as a single large particle centered at the cell's center of mass (or as a low-order multipole expansion). This can dramatically reduce the number of particle pair interactions that must be computed. Some of the most demanding high-performance computing projects do computational astrophysics using the Barnes–Hut treecode algorithm, such as DEGIMA. Algorithm The Barnes–Hut tree In a three-dimensional ''n''-body simulation, the Barnes–Hut algorithm recursively divides the ''n'' bodies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of molecules, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed wave functions as well as to observable properties such as structures, spectra, and thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the quantization of energy on a molecular scale can be obtained. Common methods are infra-red (IR) spectroscopy, nuclear magnetic r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Functional Theory
Density-functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground state) of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry. DFT has been very popular for calculations in solid-state physics since the 1970s. However, DFT was not considered accurate enough for calculations in quantum chemistry until the 1990s, when the approximations used in the theory were greatly refined to better model the exchange and correlation interactio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
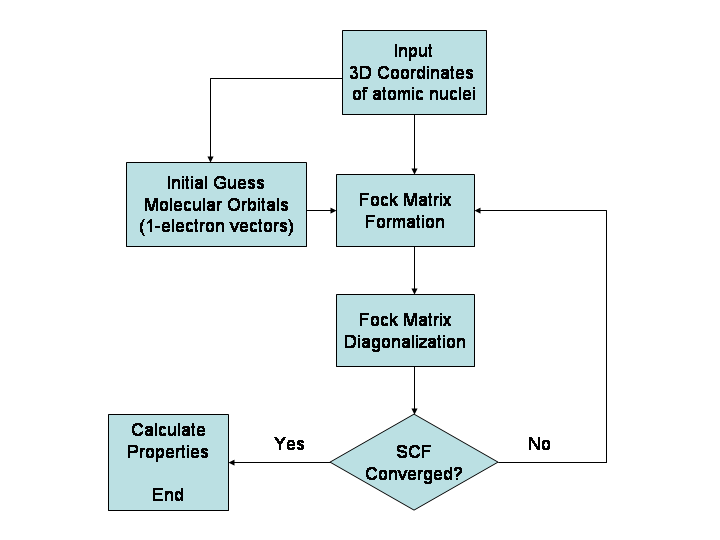
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distributi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |