|
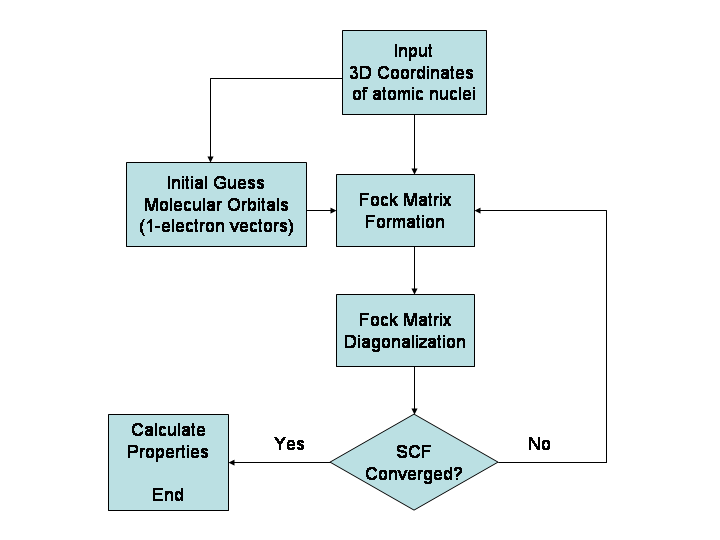
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Physics
Computational physics is the study and implementation of numerical analysis to solve problems in physics. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science. It is sometimes regarded as a subdiscipline (or offshoot) of theoretical physics, but others consider it an intermediate branch between theoretical and experimental physics — an area of study which supplements both theory and experiment. Overview In physics, different theories based on mathematical models provide very precise predictions on how systems behave. Unfortunately, it is often the case that solving the mathematical model for a particular system in order to produce a useful prediction is not feasible. This can occur, for instance, when the solution does not have a closed-form expression, or is too complicated. In such cases, numerical approximations are required. Computational physics is the subject that deals with these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unrestricted Hartree–Fock
Unrestricted Hartree–Fock (UHF) theory is the most common molecular orbital method for open shell molecules where the number of electrons of each spin are not equal. While restricted Hartree–Fock theory uses a single molecular orbital twice, one multiplied by the α spin function and the other multiplied by the β spin function in the Slater determinant, unrestricted Hartree–Fock theory uses different molecular orbitals for the α and β electrons. This has been called a ''different orbitals for different spins'' (DODS) method. The result is a pair of coupled Roothaan equations, known as the Pople–Nesbet–Berthier equations. :\mathbf^\alpha\ \mathbf^\alpha\ = \mathbf \mathbf^\alpha\ \mathbf^\alpha\ :\mathbf^\beta\ \mathbf^\beta\ = \mathbf \mathbf^\beta\ \mathbf^\beta\ Where \mathbf^\alpha\ and \mathbf^\beta\ are the Fock matrices for the \alpha\ and \beta\ orbitals, \mathbf^\alpha\ and \mathbf^\beta\ are the matrices of coefficients for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Restricted Open-shell Hartree–Fock
Restricted open-shell Hartree–Fock (ROHF) is a variant of Hartree–Fock method for open shell molecules. It uses doubly occupied molecular orbitals as far as possible and then singly occupied orbitals for the unpaired electrons. This is the simple picture for open shell molecules but it is difficult to implement. The foundations of the ROHF method were first formulated by Clemens C. J. Roothaan in a celebrated paper and then extended by various authors, see e.g. for in-depth discussions. As with restricted Hartree–Fock theory for closed shell molecules, it leads to Roothaan equations written in the form of a generalized eigenvalue problem :\mathbf \mathbf = \mathbf \mathbf \mathbf where \mathbf is the so-called Fock matrix (which is a function of \mathbf), \mathbf is a matrix of coefficients, \mathbf is the overlap matrix of the basis functions, and \epsilon is the (diagonal, by convention) matrix of orbital energies. Unlike restricted Hartree–Fock theory for closed shell ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Shell
In atomic physics and quantum chemistry, the electron configuration is the distribution of electrons of an atom or molecule (or other physical structure) in atomic or molecular orbitals. For example, the electron configuration of the neon atom is , meaning that the 1s, 2s, and 2p subshells are occupied by two, two, and six electrons, respectively. Electronic configurations describe each electron as moving independently in an orbital, in an average field created by the nuclei and all the other electrons. Mathematically, configurations are described by Slater determinants or configuration state functions. According to the laws of quantum mechanics, a level of energy is associated with each electron configuration. In certain conditions, electrons are able to move from one configuration to another by the emission or absorption of a quantum of energy, in the form of a photon. Knowledge of the electron configuration of different atoms is useful in understanding the structure o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ground State
The ground state of a quantum-mechanical system is its stationary state of lowest energy; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state. In quantum field theory, the ground state is usually called the vacuum. If more than one ground state exists, they are said to be degenerate. Many systems have degenerate ground states. Degeneracy occurs whenever there exists a unitary operator that acts non-trivially on a ground state and commutes with the Hamiltonian of the system. According to the third law of thermodynamics, a system at absolute zero temperature exists in its ground state; thus, its entropy is determined by the degeneracy of the ground state. Many systems, such as a perfect crystal lattice, have a unique ground state and therefore have zero entropy at absolute zero. It is also possible for the highest excited state to have absolute zero temperature for sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Number
In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system. To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantum numbers includes the principal, azimuthal, magnetic, and spin quantum numbers. To describe other systems, different quantum numbers are required. For subatomic particles, one needs to introduce new quantum numbers, such as the flavour of quarks, which have no classical correspondence. Quantum numbers are closely related to eigenvalues of observables. When the corresponding observable commutes with the Hamiltonian of the system, the quantum number is said to be " good", and acts as a constant of motion in the quantum dynamics. History Electronic quantum numbers In the era of the old quantum theory, starting from Max Planck's proposal of quanta in his model of blackbody radiation (1900) and Albert Einstein's adaptation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Configuration State Function
In quantum chemistry, a configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinants. A CSF must not be confused with a configuration. In general, one configuration gives rise to several CSFs; all have the same total quantum numbers for spin and spatial parts but differ in their intermediate couplings. Definition A configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinants. It is constructed to have the same quantum numbers as the wavefunction, \Psi, of the system being studied. In the method of configuration interaction, the wavefunction can be expressed as a linear combination of CSFs, that is in the form \Psi = \sum_k c_k \psi_k where \psi_k denotes the set of CSFs. The coefficients, c_k, are found by using the expansion of \Psi to compute a Hamiltonian matrix. When this is diagonalized, the eigenvectors are chosen as the expansion coefficients. CSFs rather than just Slater determinants can also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Structure
Atoms are the basic particles of the chemical elements. An atom consists of a nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished from each other by the number of protons that are in their atoms. For example, any atom that contains 11 protons is sodium, and any atom that contains 29 protons is copper. Atoms with the same number of protons but a different number of neutrons are called isotopes of the same element. Atoms are extremely small, typically around 100 picometers across. A human hair is about a million carbon atoms wide. Atoms are smaller than the shortest wavelength of visible light, which means humans cannot see atoms with conventional microscopes. They are so small that accurately predicting their behavior using classical physics is not possible due to quantum effects. More than 99.94% of an atom's mass is in the nucleus. Protons have a positive electric charge and n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
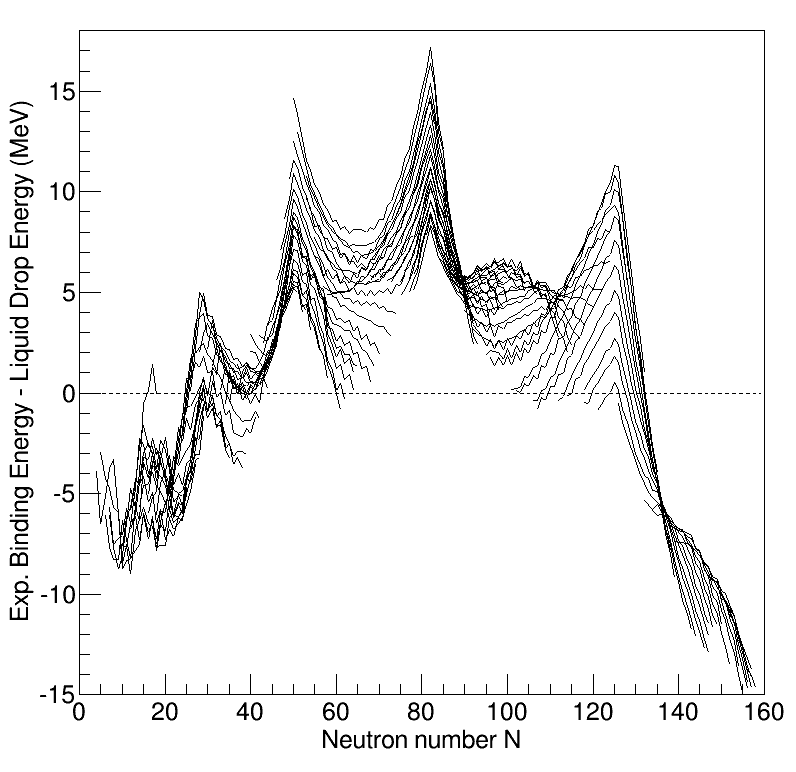
Nuclear Structure
Understanding the structure of the atomic nucleus is one of the central challenges in nuclear physics. Models The cluster model The cluster model describes the nucleus as a molecule-like collection of proton-neutron groups (e.g., alpha particles) with one or more valence neutrons occupying molecular orbitals. The liquid drop model The liquid drop model is one of the first models of nuclear structure, proposed by Carl Friedrich von Weizsäcker in 1935. It describes the nucleus as a semiclassical fluid made up of neutrons and protons, with an internal repulsive electrostatic force proportional to the number of protons. The quantum mechanical nature of these particles appears via the Pauli exclusion principle, which states that no two nucleons of the same kind can be at the same state. Thus the fluid is actually what is known as a Fermi liquid. In this model, the binding energy of a nucleus with Z protons and N neutrons is given by :E_ = a_ A - a_ A^ - a_ \frac - a_ \frac - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bogoliubov Transformation
In theoretical physics, the Bogoliubov transformation, also known as the Bogoliubov–Valatin transformation, was independently developed in 1958 by Nikolay Bogolyubov and John George Valatin for finding solutions of BCS theory in a homogeneous system. The Bogoliubov transformation is an isomorphism of either the canonical commutation relation algebra or canonical anticommutation relation algebra. This induces an autoequivalence on the respective representations. The Bogoliubov transformation is often used to diagonalize Hamiltonians, which yields the stationary solutions of the corresponding Schrödinger equation. The Bogoliubov transformation is also important for understanding the Unruh effect, Hawking radiation, Davies-Fulling radiation (moving mirror model), pairing effects in nuclear physics, and many other topics. The Bogoliubov transformation is often used to diagonalize Hamiltonians, ''with'' a corresponding transformation of the state function. Operator eigenvalues cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuclear Physics
Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter. Nuclear physics should not be confused with atomic physics, which studies the atom as a whole, including its electrons. Discoveries in nuclear physics have led to applications in many fields such as nuclear power, nuclear weapons, nuclear medicine and magnetic resonance imaging, industrial and agricultural isotopes, ion implantation in materials engineering, and radiocarbon dating in geology and archaeology. Such applications are studied in the field of nuclear engineering. Particle physics evolved out of nuclear physics and the two fields are typically taught in close association. Nuclear astrophysics, the application of nuclear physics to astrophysics, is crucial in explaining the inner workings of stars and the origin of the chemical elements. History The history of nuclear physics as a discipline ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |