|
Kepler Problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force that varies in strength as the inverse square of the distance between them. The force may be either attractive or repulsive. The problem is to find the position or speed of the two bodies over time given their masses, positions, and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit using six orbital elements. The Kepler problem is named after Johannes Kepler, who proposed Kepler's laws of planetary motion (which are part of classical mechanics and solved the problem for the orbits of the planets) and investigated the types of forces that would result in orbits obeying those laws (called ''Kepler's inverse problem''). For a discussion of the Kepler problem specific to radial orbits, see Radial trajectory. General relativity provides more accurate solutions to the two-body problem, especially in stron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-body Problem
In classical mechanics, the two-body problem is to calculate and predict the motion of two massive bodies that are orbiting each other in space. The problem assumes that the two bodies are point particles that interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored. The most prominent example of the classical two-body problem is the gravitational case (see also Kepler problem), arising in astronomy for predicting the orbits (or escapes from orbit) of objects such as satellites, planets, and stars. A two-point-particle model of such a system nearly always describes its behavior well enough to provide useful insights and predictions. A simpler "one body" model, the " central-force problem", treats one object as the immobile source of a force acting on the other. One then seeks to predict the motion of the single remaining mobile object. Such an approximation can give useful results when one object is much ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitation
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force between objects and the Earth. This force is dominated by the combined gravitational interactions of particles but also includes effect of the Earth's rotation. Gravity gives weight to physical objects and is essential to understanding the mechanisms responsible for surface water waves and lunar tides. Gravity also has many important biological functions, helping to guide the growth of plants through the process of gravitropism and influencing the circulation of fluids in multicellular organisms. The gravitational attraction between primordial hydrogen and clumps of dark matter in the early universe caused the hydrogen gas to coalesce, eventually condensing and fusing to form stars. At larger scales this results in galaxies and clusters ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler%27s Laws Of Planetary Motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, which was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in the heliocentric theory of Nicolaus Copernicus with elliptical orbits and explained how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law establishes that when a planet is closer to the Sun, it travels fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Laws Of Motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows: # A body remains at rest, or in motion at a constant speed in a straight line, unless it is acted upon by a force. # At any instant of time, the net force on a body is equal to the body's acceleration multiplied by its mass or, equivalently, the rate at which the body's momentum is changing with time. # If two bodies exert forces on each other, these forces have the same magnitude but opposite directions. The three laws of motion were first stated by Isaac Newton in his ''Philosophiæ Naturalis Principia Mathematica'' (''Mathematical Principles of Natural Philosophy''), originally published in 1687. Newton used them to investigate and explain the motion of many physical objects and systems. In the time since Newton, new insights, especially around t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosophiæ Naturalis Principia Mathematica
(English: ''The Mathematical Principles of Natural Philosophy''), often referred to as simply the (), is a book by Isaac Newton that expounds Newton's laws of motion and his law of universal gravitation. The ''Principia'' is written in Latin and comprises three volumes, and was authorized, imprimatur, by Samuel Pepys, then-President of the Royal Society on 5 July 1686 and first published in 1687. The is considered one of the most important works in the history of science. The French mathematical physicist Alexis Clairaut assessed it in 1747: "The famous book of ''Mathematical Principles of Natural Philosophy'' marked the epoch of a great revolution in physics. The method followed by its illustrious author Sir Newton ... spread the light of mathematics on a science which up to then had remained in the darkness of conjectures and hypotheses." The French scientist Joseph-Louis Lagrange described it as "the greatest production of the human mind". French polymath Pierre-Simon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, achieved the Unification of theories in physics#Unification of gravity and astronomy, first great unification in physics and established classical mechanics. Newton also made seminal contributions to optics, and Leibniz–Newton calculus controversy, shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating calculus, infinitesimal calculus, though he developed calculus years before Leibniz. Newton contributed to and refined the scientific method, and his work is considered the most influential in bringing forth modern science. In the , Newton formulated the Newton's laws of motion, laws of motion and Newton's law of universal g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
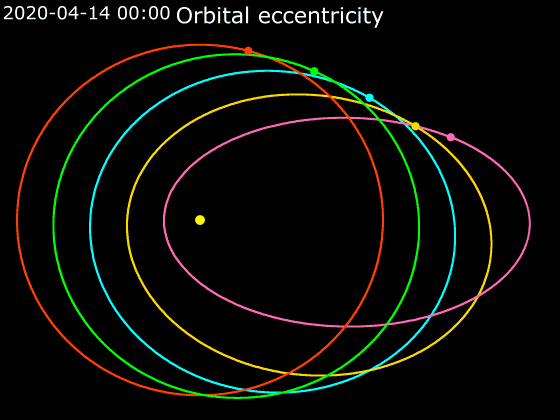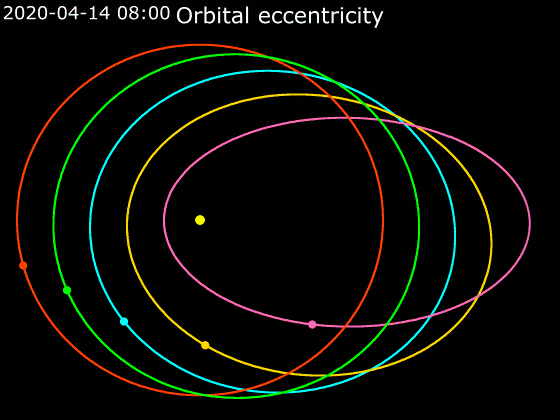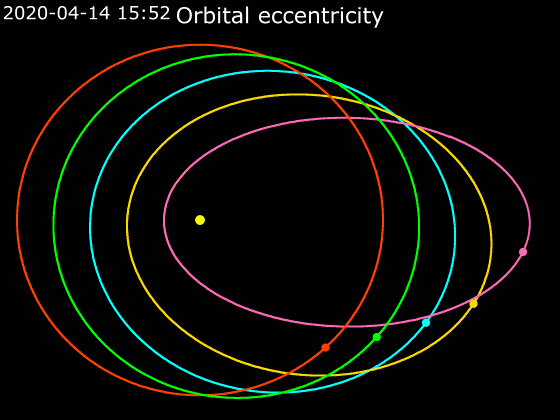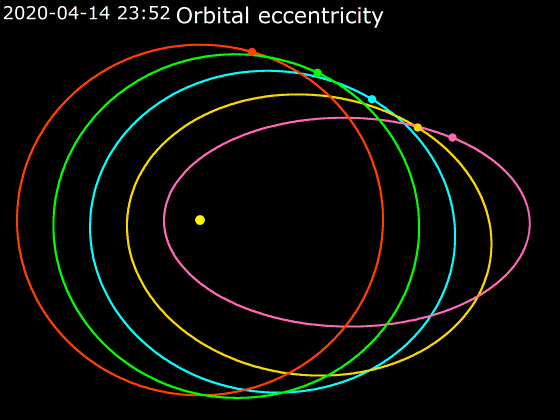
Elliptic Orbit
In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses. In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit. Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies (m_1) and (m_2), the orbital speed (v\,) of one body traveling along an elliptical orbit can be computed from the vis-viva equation as: :v = \sqrt where: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tycho Brahe
Tycho Brahe ( ; ; born Tyge Ottesen Brahe, ; 14 December 154624 October 1601), generally called Tycho for short, was a Danish astronomer of the Renaissance, known for his comprehensive and unprecedentedly accurate astronomical observations. He was known during his lifetime as an astronomer, astrologer, and alchemist. He was the last major astronomer before the invention of the telescope. Tycho Brahe has also been described as the greatest pre-telescopic astronomer. In 1572, Tycho noticed a completely SN 1572, new star that was brighter than any star or planet. Astonished by the existence of a star that ought not to have been there, he devoted himself to the creation of ever more accurate instruments of measurement over the next fifteen years (1576–1591). Frederick II of Denmark, King Frederick II granted Tycho an estate on the island of Hven and the money to build Uraniborg, the first large observatory in Christian Europe. He later worked underground at Stjerneborg, where he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Age Of Enlightenment
The Age of Enlightenment (also the Age of Reason and the Enlightenment) was a Europe, European Intellect, intellectual and Philosophy, philosophical movement active from the late 17th to early 19th century. Chiefly valuing knowledge gained through rationalism and empiricism, the Enlightenment was concerned with a wide range of social and Politics, political ideals such as natural law, liberty, and progress, toleration and fraternity (philosophy), fraternity, constitutional government, and the formal separation of church and state. The Enlightenment was preceded by and overlapped the Scientific Revolution, which included the work of Johannes Kepler, Galileo Galilei, Francis Bacon, Pierre Gassendi, Christiaan Huygens and Isaac Newton, among others, as well as the philosophy of Descartes, Hobbes, Spinoza, Leibniz, and John Locke. The dating of the period of the beginning of the Enlightenment can be attributed to the publication of René Descartes' ''Discourse on the Method'' in 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace–Runge–Lenz Vector
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector (geometric), vector used chiefly to describe the shape and orientation of the orbit (celestial mechanics), orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For Two-body problem, two bodies interacting by Newton's law of universal gravitation, Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be ''Conservation law, conserved''. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square law, inverse square of the distance between them; such problems are called Kepler problems. Thus the hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bertrand's Theorem
In classical mechanics, Bertrand's theorem states that among central-force potentials with bound orbits, there are only two types of central-force (radial) scalar potentials with the property that all bound orbits are also closed orbits. The first such potential is an inverse-square central force such as the gravitational or electrostatic potential: V(r) = -\frac with force f(r) = -\frac = -\frac. The second is the radial harmonic oscillator potential: V(r) = \frac k r^2 with force f(r) = -\frac = -k r. The theorem is named after its discoverer, Joseph Bertrand. Derivation All attractive central forces can produce circular orbits, which are naturally closed orbits. The only requirement is that the central force exactly equals the centripetal force, which determines the required angular velocity for a given circular radius. Non-central forces (i.e., those that depend on the angular variables as well as the radius) are ignored here, since they do not produce circu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Harmonic Oscillator
In mechanics and physics, simple harmonic motion (sometimes abbreviated as ) is a special type of periodic function, periodic motion an object experiences by means of a restoring force whose magnitude is directly proportionality (mathematics), proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely (if uninhibited by friction or any other dissipation of energy). Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring (device), spring when it is subject to the linear elasticity (physics), elastic restoring force given by Hooke's law. The motion is sinusoidal in time and demonstrates a single resonance, resonant frequency. Other phenomena can be modeled by simple harmonic motion, including the motion of a pendulum, simple pendulum, although for it to b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |