Spinor Representation on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 Spinors form a
Spinors form a
p. 151
/ref> More specifically, instead of representing spinors as complex-valued 2D column vectors as Pauli had done, they represented them as complex-valued 2 × 2 matrices in which only the elements of the left column are non-zero. In this manner the spinor space became a minimal left ideal in .Pertti Lounesto: ''Clifford algebras and spinors'', London Mathematical Society Lecture Notes Series 286, Cambridge University Press, Second Edition 2001, , p. 148 f. an
p. 327 f.
/ref> In 1947 Marcel Riesz constructed spinor spaces as elements of a minimal left ideal of
 In
In geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
and physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, spinors (pronounced "spinner" IPA ) are elements of a complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
that can be associated with Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " ...
) rotation, but unlike geometric vectors and tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
s, a spinor transforms to its negative when the
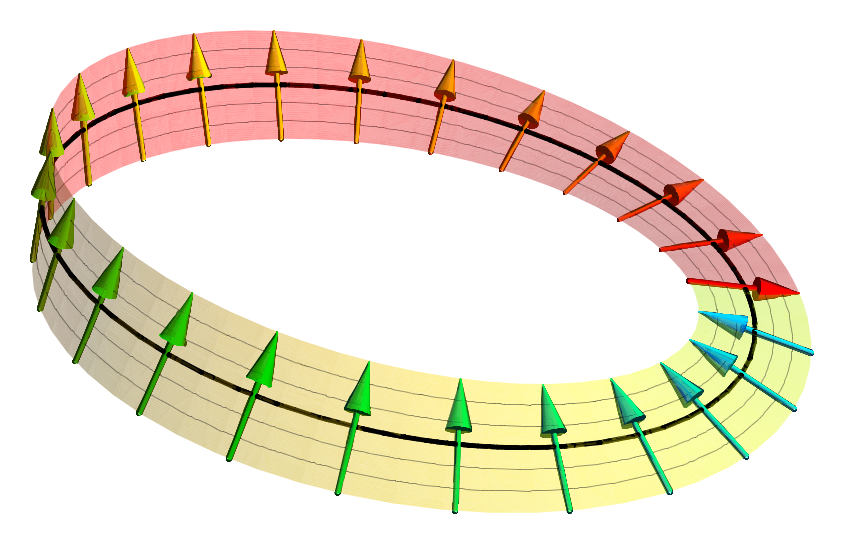
space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections
Section, Sectioning, or Sectioned may refer to:
Arts, entertainment and media
* Section (music), a complete, but not independent, musical idea
* Section (typography), a subdivision, especially of a chapter, in books and documents
** Section sig ...
of vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to eve ...
s – in the case of the exterior algebra
In mathematics, the exterior algebra or Grassmann algebra of a vector space V is an associative algebra that contains V, which has a product, called exterior product or wedge product and denoted with \wedge, such that v\wedge v=0 for every vector ...
bundle of the cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold. It may be described also as the dual bundle to the tangent bundle. This m ...
, they thus become "square roots" of differential form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications ...
s).
It is also possible to associate a substantially similar notion of spinor to Minkowski space
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model helps show how a ...
, in which case the Lorentz transformation
In physics, the Lorentz transformations are a six-parameter family of Linear transformation, linear coordinate transformation, transformations from a Frame of Reference, coordinate frame in spacetime to another frame that moves at a constant vel ...
s of special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity,
"On the Ele ...
play the role of rotations. Spinors were introduced in geometry by Élie Cartan
Élie Joseph Cartan (; 9 April 1869 – 6 May 1951) was an influential French mathematician who did fundamental work in the theory of Lie groups, differential systems (coordinate-free geometric formulation of PDEs), and differential geometry. He ...
in 1913. In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum
Spin is an intrinsic form of angular momentum carried by elementary particles, and thus by composite particles such as hadrons, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic ...
, or "spin", of the electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
and other subatomic particles.
Spinors are characterized by the specific way in which they behave under rotations. They change in different ways depending not just on the overall final rotation, but the details of how that rotation was achieved (by a continuous path in the rotation group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. ...
). There are two topologically distinguishable classes (homotopy class
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. A ...
es) of paths through rotations that result in the same overall rotation, as illustrated by the belt trick
In mathematics and physics, the plate trick, also known as Dirac's string trick (after Paul Dirac, who introduced and popularized it), the belt trick, or the Balinese cup trick (it appears in the Balinese candle dance), is any of several demonstr ...
puzzle. These two inequivalent classes yield spinor transformations of opposite sign. The spin group
In mathematics the spin group, denoted Spin(''n''), page 15 is a Lie group whose underlying manifold is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathbb_2 \to \o ...
is the group of all rotations keeping track of the class. It doubly covers the rotation group, since each rotation can be obtained in two inequivalent ways as the endpoint of a path. The space of spinors by definition is equipped with a (complex) linear representation
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essen ...
of the spin group, meaning that elements of the spin group act as linear transformations on the space of spinors, in a way that genuinely depends on the homotopy class. In mathematical terms, spinors are described by a double-valued projective representation
In the field of representation theory in mathematics, a projective representation of a group ''G'' on a vector space ''V'' over a field ''F'' is a group homomorphism from ''G'' to the projective linear group
\mathrm(V) = \mathrm(V) / F^*,
where G ...
of the rotation group SO(3)
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space \R^3 under the operation of composition.
By definition, a rotation about the origin is a ...
.
Although spinors can be defined purely as elements of a representation space of the spin group (or its Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi ident ...
of infinitesimal rotations), they are typically defined as elements of a vector space that carries a linear representation of the Clifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real number ...
. The Clifford algebra is an associative algebra
In mathematics, an associative algebra ''A'' over a commutative ring (often a field) ''K'' is a ring ''A'' together with a ring homomorphism from ''K'' into the center of ''A''. This is thus an algebraic structure with an addition, a mult ...
that can be constructed from Euclidean space and its inner product in a basis-independent way. Both the spin group and its Lie algebra are embedded inside the Clifford algebra in a natural way, and in applications the Clifford algebra is often the easiest to work with. A Clifford space operates on a spinor space, and the elements of a spinor space are spinors. After choosing an orthonormal
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal unit vectors. A unit vector means that the vector has a length of 1, which is also known as normalized. Orthogonal means that the vectors are all perpe ...
basis of Euclidean space, a representation of the Clifford algebra is generated by gamma matrices
In mathematical physics, the gamma matrices, \ \left\\ , also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra \ \mathr ...
, matrices that satisfy a set of canonical anti-commutation relations. The spinors are the column vectors on which these matrices act. In three Euclidean dimensions, for instance, the Pauli spin matrices are a set of gamma matrices, and the two-component complex column vectors on which these matrices act are spinors. However, the particular matrix representation of the Clifford algebra, hence what precisely constitutes a "column vector" (or spinor), involves the choice of basis and gamma matrices in an essential way. As a representation of the spin group, this realization of spinors as (complex) column vectors will either be irreducible if the dimension is odd, or it will decompose into a pair of so-called "half-spin" or Weyl representations if the dimension is even.
Introduction
What characterizes spinors and distinguishes them from geometric vectors and other tensors is subtle. Consider applying a rotation to the coordinates of a system. No object in the system itself has moved, only the coordinates have, so there will always be a compensating change in those coordinate values when applied to any object of the system. Geometrical vectors, for example, have components that will undergo ''the same'' rotation as the coordinates. More broadly, anytensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
associated with the system (for instance, the stress of some medium) also has coordinate descriptions that adjust to compensate for changes to the coordinate system itself.
Spinors do not appear at this level of the description of a physical system, when one is concerned only with the properties of a single isolated rotation of the coordinates. Rather, spinors appear when we imagine that instead of a single rotation, the coordinate system is gradually ( continuously) rotated between some initial and final configuration. For any of the familiar and intuitive ("tensorial") quantities associated with the system, the transformation law does not depend on the precise details of how the coordinates arrived at their final configuration. Spinors, on the other hand, are constructed in such a way that makes them ''sensitive'' to how the gradual rotation of the coordinates arrived there: They exhibit path-dependence. It turns out that, for any final configuration of the coordinates, there are actually two (" topologically") inequivalent ''gradual'' (continuous) rotations of the coordinate system that result in this same configuration. This ambiguity is called the homotopy class
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. A ...
of the gradual rotation. The belt trick
In mathematics and physics, the plate trick, also known as Dirac's string trick (after Paul Dirac, who introduced and popularized it), the belt trick, or the Balinese cup trick (it appears in the Balinese candle dance), is any of several demonstr ...
(shown, in which both ends of the rotated object are physically tethered to an external reference) demonstrates two different rotations, one through an angle of 2 and the other through an angle of 4, having the same final configurations but different classes. Spinors actually exhibit a sign-reversal that genuinely depends on this homotopy class. This distinguishes them from vectors and other tensors, none of which can feel the class.
Spinors can be exhibited as concrete objects using a choice of Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
. In three Euclidean dimensions, for instance, spinors can be constructed by making a choice of Pauli spin matrices corresponding to ( angular momenta about) the three coordinate axes. These are 2×2 matrices with complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
entries, and the two-component complex column vector
In linear algebra, a column vector with elements is an m \times 1 matrix consisting of a single column of entries, for example,
\boldsymbol = \begin x_1 \\ x_2 \\ \vdots \\ x_m \end.
Similarly, a row vector is a 1 \times n matrix for some , c ...
s on which these matrices act by matrix multiplication
In mathematics, specifically in linear algebra, matrix multiplication is a binary operation that produces a matrix (mathematics), matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the n ...
are the spinors. In this case, the spin group is isomorphic to the group of 2×2 unitary matrices with determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
one, which naturally sits inside the matrix algebra. This group acts by conjugation on the real vector space spanned by the Pauli matrices themselves, realizing it as a group of rotations among them, but it also acts on the column vectors (that is, the spinors).
More generally, a Clifford algebra can be constructed from any vector space ''V'' equipped with a (nondegenerate) quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two (" form" is another name for a homogeneous polynomial). For example,
4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong t ...
, such as Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
with its standard dot product or Minkowski space
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model helps show how a ...
with its standard Lorentz metric. The space of spinors is the space of column vectors with components. The orthogonal Lie algebra (i.e., the infinitesimal "rotations") and the spin group associated to the quadratic form are both (canonically) contained in the Clifford algebra, so every Clifford algebra representation also defines a representation of the Lie algebra and the spin group. Depending on the dimension and metric signature
In mathematics, the signature of a metric tensor ''g'' (or equivalently, a real quadratic form thought of as a real symmetric bilinear form on a finite-dimensional vector space) is the number (counted with multiplicity) of positive, negative and z ...
, this realization of spinors as column vectors may be irreducible or it may decompose into a pair of so-called "half-spin" or Weyl representations. When the vector space ''V'' is four-dimensional, the algebra is described by the gamma matrices
In mathematical physics, the gamma matrices, \ \left\\ , also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra \ \mathr ...
.
Mathematical definition
The space of spinors is formally defined as the fundamental representation of theClifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real number ...
. (This may or may not decompose into irreducible representations.) The space of spinors may also be defined as a spin representation
In mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature (i.e., including indefinite orthogonal groups). More precisely, they are two equi ...
of the orthogonal Lie algebra. These spin representations are also characterized as the finite-dimensional projective representations of the special orthogonal group that do not factor through linear representations. Equivalently, a spinor is an element of a finite-dimensional group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of bijective linear transformations of a vector space to itself (i.e. vector space automorphisms); in particular, they can be used ...
of the spin group
In mathematics the spin group, denoted Spin(''n''), page 15 is a Lie group whose underlying manifold is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathbb_2 \to \o ...
on which the center acts non-trivially.
Overview
There are essentially two frameworks for viewing the notion of a spinor: the ''representation theoretic point of view'' and the ''geometric point of view''.Representation theoretic point of view
From a representation theoretic point of view, one knows beforehand that there are some representations of theLie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi ident ...
of the orthogonal group
In mathematics, the orthogonal group in dimension , denoted , is the Group (mathematics), group of isometry, distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by ...
that cannot be formed by the usual tensor constructions. These missing representations are then labeled the spin representation
In mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature (i.e., including indefinite orthogonal groups). More precisely, they are two equi ...
s, and their constituents ''spinors''. From this view, a spinor must belong to a representation of the double cover of the rotation group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. ...
, or more generally of a double cover of the generalized special orthogonal group on spaces with a metric signature
In mathematics, the signature of a metric tensor ''g'' (or equivalently, a real quadratic form thought of as a real symmetric bilinear form on a finite-dimensional vector space) is the number (counted with multiplicity) of positive, negative and z ...
of . These double covers are Lie groups
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Euclidean space, whereas ...
, called the spin group
In mathematics the spin group, denoted Spin(''n''), page 15 is a Lie group whose underlying manifold is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathbb_2 \to \o ...
s or . All the properties of spinors, and their applications and derived objects, are manifested first in the spin group. Representations of the double covers of these groups yield double-valued projective representation
In the field of representation theory in mathematics, a projective representation of a group ''G'' on a vector space ''V'' over a field ''F'' is a group homomorphism from ''G'' to the projective linear group
\mathrm(V) = \mathrm(V) / F^*,
where G ...
s of the groups themselves. (This means that the action of a particular rotation on vectors in the quantum Hilbert space is only defined up to a sign.)
In summary, given a representation specified by the data where is a vector space over or and is a homomorphism , a spinor is an element of the vector space .
Geometric point of view
From a geometrical point of view, one can explicitly construct the spinors and then examine how they behave under the action of the relevant Lie groups. This latter approach has the advantage of providing a concrete and elementary description of what a spinor is. However, such a description becomes unwieldy when complicated properties of the spinors, such as Fierz identities, are needed.Clifford algebras
The language ofClifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real number ...
s (sometimes called geometric algebra
In mathematics, a geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric pr ...
s) provides a complete picture of the spin representations of all the spin groups, and the various relationships between those representations, via the classification of Clifford algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the finite-dimensional real and complex Clifford algebras for a nondegenerate quadratic form have been completely classified as rings. In each c ...
. It largely removes the need for ''ad hoc'' constructions.
In detail, let ''V'' be a finite-dimensional complex vector space with nondegenerate symmetric bilinear form ''g''. The Clifford algebra is the algebra generated by ''V'' along with the anticommutation relation . It is an abstract version of the algebra generated by the gamma
Gamma (; uppercase , lowercase ; ) is the third letter of the Greek alphabet. In the system of Greek numerals it has a value of 3. In Ancient Greek, the letter gamma represented a voiced velar stop . In Modern Greek, this letter normally repr ...
or Pauli matrices
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () ...
. If ''V'' = , with the standard form we denote the Clifford algebra by Cℓ''n''(). Since by the choice of an orthonormal basis every complex vector space with non-degenerate form is isomorphic to this standard example, this notation is abused more generally if . If is even, is isomorphic as an algebra (in a non-unique way) to the algebra of complex matrices (by the Artin–Wedderburn theorem and the easy to prove fact that the Clifford algebra is central simple). If is odd, is isomorphic to the algebra of two copies of the complex matrices. Therefore, in either case has a unique (up to isomorphism) irreducible representation (also called simple Clifford module), commonly denoted by Δ, of dimension 2 'n''/2/sup>. Since the Lie algebra is embedded as a Lie subalgebra in equipped with the Clifford algebra commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.
Group theory
The commutator of two elements, ...
as Lie bracket, the space Δ is also a Lie algebra representation of called a spin representation
In mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature (i.e., including indefinite orthogonal groups). More precisely, they are two equi ...
. If ''n'' is odd, this Lie algebra representation is irreducible. If ''n'' is even, it splits further into two irreducible representations called the Weyl or ''half-spin representations''.
Irreducible representations over the reals in the case when ''V'' is a real vector space are much more intricate, and the reader is referred to the Clifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real number ...
article for more details.
Spin groups
vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
, usually over the complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
, equipped with a linear group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of bijective linear transformations of a vector space to itself (i.e. vector space automorphisms); in particular, they can be used ...
of the spin group
In mathematics the spin group, denoted Spin(''n''), page 15 is a Lie group whose underlying manifold is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathbb_2 \to \o ...
that does not factor through a representation of the group of rotations (see diagram). The spin group is the group of rotations keeping track of the homotopy class. Spinors are needed to encode basic information about the topology of the group of rotations because that group is not simply connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every Path (topology), path between two points can be continuously transformed into any other such path while preserving ...
, but the simply connected spin group is its double cover. So for every rotation there are two elements of the spin group that represent it. Geometric vectors and other tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
s cannot feel the difference between these two elements, but they produce ''opposite'' signs when they affect any spinor under the representation. Thinking of the elements of the spin group as homotopy classes of one-parameter families of rotations, each rotation is represented by two distinct homotopy classes of paths to the identity. If a one-parameter family of rotations is visualized as a ribbon in space, with the arc length parameter of that ribbon being the parameter (its tangent, normal, binormal frame actually gives the rotation), then these two distinct homotopy classes are visualized in the two states of the belt trick
In mathematics and physics, the plate trick, also known as Dirac's string trick (after Paul Dirac, who introduced and popularized it), the belt trick, or the Balinese cup trick (it appears in the Balinese candle dance), is any of several demonstr ...
puzzle (above). The space of spinors is an auxiliary vector space that can be constructed explicitly in coordinates, but ultimately only exists up to isomorphism in that there is no "natural" construction of them that does not rely on arbitrary choices such as coordinate systems. A notion of spinors can be associated, as such an auxiliary mathematical object, with any vector space equipped with a quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two (" form" is another name for a homogeneous polynomial). For example,
4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong t ...
such as Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
with its standard dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
, or Minkowski space
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model helps show how a ...
with its Lorentz metric. In the latter case, the "rotations" include the Lorentz boost
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation ...
s, but otherwise the theory is substantially similar.
Spinor fields in physics
The constructions given above, in terms of Clifford algebra or representation theory, can be thought of as defining spinors as geometric objects in zero-dimensionalspace-time
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three-dimensional space, three dimensions of space and the one dimension of time into a single four-dimensional continuum (measurement), continu ...
. To obtain the spinors of physics, such as the Dirac spinor
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain comb ...
, one extends the construction to obtain a spin structure on 4-dimensional space-time (Minkowski space
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model helps show how a ...
). Effectively, one starts with the tangent manifold of space-time, each point of which is a 4-dimensional vector space with SO(3,1) symmetry, and then builds the spin group
In mathematics the spin group, denoted Spin(''n''), page 15 is a Lie group whose underlying manifold is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathbb_2 \to \o ...
at each point. The neighborhoods of points are endowed with concepts of smoothness and differentiability: the standard construction is one of a fiber bundle
In mathematics, and particularly topology, a fiber bundle ( ''Commonwealth English'': fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a pr ...
, the fibers of which are affine spaces transforming under the spin group. After constructing the fiber bundle, one may then consider differential equations, such as the Dirac equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac ...
, or the Weyl equation
In physics, particularly in quantum field theory, the Weyl equation is a relativistic wave equation for describing massless spin-1/2 particles called Weyl fermions. The equation is named after Hermann Weyl. The Weyl fermions are one of the three ...
on the fiber bundle. These equations (Dirac or Weyl) have solutions that are plane wave
In physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of ...
s, having symmetries characteristic of the fibers, ''i.e.'' having the symmetries of spinors, as obtained from the (zero-dimensional) Clifford algebra/spin representation theory described above. Such plane-wave solutions (or other solutions) of the differential equations can then properly be called fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles i ...
s; fermions have the algebraic qualities of spinors. By general convention, the terms "fermion" and "spinor" are often used interchangeably in physics, as synonyms of one-another.
It appears that all fundamental particles in nature that are spin-1/2 are described by the Dirac equation, with the possible exception of the neutrino
A neutrino ( ; denoted by the Greek letter ) is an elementary particle that interacts via the weak interaction and gravity. The neutrino is so named because it is electrically neutral and because its rest mass is so small ('' -ino'') that i ...
. There does not seem to be any ''a priori'' reason why this would be the case. A perfectly valid choice for spinors would be the non-complexified version of , the Majorana spinor. There also does not seem to be any particular prohibition to having Weyl spinors appear in nature as fundamental particles.
The Dirac, Weyl, and Majorana spinors are interrelated, and their relation can be elucidated on the basis of real geometric algebra. Dirac and Weyl spinors are complex representations while Majorana spinors are real representations.
Weyl spinors are insufficient to describe massive particles, such as electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
s, since the Weyl plane-wave solutions necessarily travel at the speed of light; for massive particles, the Dirac equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac ...
is needed. The initial construction of the Standard Model
The Standard Model of particle physics is the Scientific theory, theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions – excluding gravity) in the unive ...
of particle physics starts with both the electron and the neutrino as massless Weyl spinors; the Higgs mechanism
In the Standard Model of particle physics, the Higgs mechanism is essential to explain the Mass generation, generation mechanism of the property "mass" for gauge bosons. Without the Higgs mechanism, all bosons (one of the two classes of particles ...
gives electrons a mass; the classical neutrino
A neutrino ( ; denoted by the Greek letter ) is an elementary particle that interacts via the weak interaction and gravity. The neutrino is so named because it is electrically neutral and because its rest mass is so small ('' -ino'') that i ...
remained massless, and was thus an example of a Weyl spinor. However, because of observed neutrino oscillation
Neutrino oscillation is a quantum mechanics, quantum mechanical phenomenon in which a neutrino created with a specific lepton lepton number, family number ("lepton flavor": electron, muon, or tau lepton, tau) can later be Quantum measurement, mea ...
, it is now believed that they are not Weyl spinors, but perhaps instead Majorana spinors. It is not known whether Weyl spinor fundamental particles exist in nature.
The situation for condensed matter physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and elec ...
is different: one can construct two and three-dimensional "spacetimes" in a large variety of different physical materials, ranging from semiconductor
A semiconductor is a material with electrical conductivity between that of a conductor and an insulator. Its conductivity can be modified by adding impurities (" doping") to its crystal structure. When two regions with different doping level ...
s to far more exotic materials. In 2015, an international team led by Princeton University
Princeton University is a private university, private Ivy League research university in Princeton, New Jersey, United States. Founded in 1746 in Elizabeth, New Jersey, Elizabeth as the College of New Jersey, Princeton is the List of Colonial ...
scientists announced that they had found a quasiparticle
In condensed matter physics, a quasiparticle is a concept used to describe a collective behavior of a group of particles that can be treated as if they were a single particle. Formally, quasiparticles and collective excitations are closely relate ...
that behaves as a Weyl fermion.
Spinors in representation theory
One major mathematical application of the construction of spinors is to make possible the explicit construction oflinear representation
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essen ...
s of the Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi ident ...
s of the special orthogonal group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. ...
s, and consequently spinor representations of the groups themselves. At a more profound level, spinors have been found to be at the heart of approaches to the Atiyah–Singer index theorem, and to provide constructions in particular for discrete series representations of semisimple groups.
The spin representations of the special orthogonal Lie algebras are distinguished from the tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
representations given by Weyl's construction by the weights. Whereas the weights of the tensor representations are integer linear combinations of the roots of the Lie algebra, those of the spin representations are half-integer linear combinations thereof. Explicit details can be found in the spin representation
In mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature (i.e., including indefinite orthogonal groups). More precisely, they are two equi ...
article.
Attempts at intuitive understanding
The spinor can be described, in simple terms, as "vectors of a space the transformations of which are related in a particular way to rotations in physical space". Stated differently: Several ways of illustrating everyday analogies have been formulated in terms of the plate trick, tangloids and other examples of orientation entanglement. Nonetheless, the concept is generally considered notoriously difficult to understand, as illustrated byMichael Atiyah
Sir Michael Francis Atiyah (; 22 April 1929 – 11 January 2019) was a British-Lebanese mathematician specialising in geometry. His contributions include the Atiyah–Singer index theorem and co-founding topological K-theory. He was awarded the ...
's statement that is recounted by Dirac's biographer Graham Farmelo:
History
The most general mathematical form of spinors was discovered byÉlie Cartan
Élie Joseph Cartan (; 9 April 1869 – 6 May 1951) was an influential French mathematician who did fundamental work in the theory of Lie groups, differential systems (coordinate-free geometric formulation of PDEs), and differential geometry. He ...
in 1913. The word "spinor" was coined by Paul Ehrenfest
Paul Ehrenfest (; 18 January 1880 – 25 September 1933) was an Austrian Theoretical physics, theoretical physicist who made major contributions to statistical mechanics and its relation to quantum physics, quantum mechanics, including the theory ...
in his work on quantum physics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
.
Spinors were first applied to mathematical physics
Mathematical physics is the development of mathematics, mathematical methods for application to problems in physics. The ''Journal of Mathematical Physics'' defines the field as "the application of mathematics to problems in physics and the de ...
by Wolfgang Pauli
Wolfgang Ernst Pauli ( ; ; 25 April 1900 – 15 December 1958) was an Austrian theoretical physicist and a pioneer of quantum mechanics. In 1945, after having been nominated by Albert Einstein, Pauli received the Nobel Prize in Physics "for the ...
in 1927, when he introduced his spin matrices. The following year, Paul Dirac
Paul Adrien Maurice Dirac ( ; 8 August 1902 – 20 October 1984) was an English mathematician and Theoretical physics, theoretical physicist who is considered to be one of the founders of quantum mechanics. Dirac laid the foundations for bot ...
discovered the fully relativistic theory of electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
spin by showing the connection between spinors and the Lorentz group
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physi ...
. By the 1930s, Dirac, Piet Hein and others at the Niels Bohr Institute
The Niels Bohr Institute () is a research institute of the University of Copenhagen. The research of the institute spans astronomy, geophysics, nanotechnology, particle physics, quantum mechanics, and biophysics.
Overview
The institute was foun ...
(then known as the Institute for Theoretical Physics of the University of Copenhagen) created toys such as Tangloids to teach and model the calculus of spinors.
Spinor spaces were represented as left ideal
In mathematics, and more specifically in ring theory, an ideal of a ring is a special subset of its elements. Ideals generalize certain subsets of the integers, such as the even numbers or the multiples of 3. Addition and subtraction of even n ...
s of a matrix algebra in 1930, by Gustave Juvett and by Fritz Sauter.Pertti Lounesto: '' Crumeyrolle's bivectors and spinors'', pp. 137–166, In: Rafał Abłamowicz, Pertti Lounesto (eds.): ''Clifford algebras and spinor structures: A Special Volume Dedicated to the Memory of Albert Crumeyrolle (1919–1992)'', , 1995p. 151
/ref> More specifically, instead of representing spinors as complex-valued 2D column vectors as Pauli had done, they represented them as complex-valued 2 × 2 matrices in which only the elements of the left column are non-zero. In this manner the spinor space became a minimal left ideal in .Pertti Lounesto: ''Clifford algebras and spinors'', London Mathematical Society Lecture Notes Series 286, Cambridge University Press, Second Edition 2001, , p. 148 f. an
p. 327 f.
/ref> In 1947 Marcel Riesz constructed spinor spaces as elements of a minimal left ideal of
Clifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real number ...
s. In 1966/1967, David Hestenes replaced spinor spaces by the even subalgebra Cℓ01,3() of the spacetime algebra
In mathematical physics, spacetime algebra (STA) is the application of Clifford algebra Cl1,3(R), or equivalently the geometric algebra to physics. Spacetime algebra provides a "unified, coordinate-free formulation for all of special relativity, ...
Cℓ1,3(). As of the 1980s, the theoretical physics group at Birkbeck College
Birkbeck, University of London (formally Birkbeck College, University of London), is a public research university located in London, England, and a member institution of the University of London. Established in 1823 as the London Mechanics' ...
around David Bohm
David Joseph Bohm (; 20 December 1917 – 27 October 1992) was an American scientist who has been described as one of the most significant Theoretical physics, theoretical physicists of the 20th centuryDavid Peat Who's Afraid of Schrödinger' ...
and Basil Hiley has been developing algebraic approaches to quantum theory that build on Sauter and Riesz' identification of spinors with minimal left ideals.
Examples
Some simple examples of spinors in low dimensions arise from considering the even-graded subalgebras of the Clifford algebra . This is an algebra built up from an orthonormal basis of mutually orthogonal vectors under addition and multiplication, ''p'' of which have norm +1 and ''q'' of which have norm −1, with the product rule for the basis vectorsTwo dimensions
The Clifford algebra Cℓ2,0() is built up from a basis of one unit scalar, 1, two orthogonal unit vectors, ''σ''1 and ''σ''2, and one unitpseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
A pseudoscalar, when multiplied by an ordinary vector, becomes a '' pseudovector'' ...
. From the definitions above, it is evident that , and .
The even subalgebra Cℓ02,0(), spanned by ''even-graded'' basis elements of Cℓ2,0(), determines the space of spinors via its representations. It is made up of real linear combinations of 1 and ''σ''1''σ''2. As a real algebra, Cℓ02,0() is isomorphic to the field of complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
. As a result, it admits a conjugation operation (analogous to complex conjugation
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - ...
), sometimes called the ''reverse'' of a Clifford element, defined by
which, by the Clifford relations, can be written
The action of an even Clifford element on vectors, regarded as 1-graded elements of Cℓ2,0(), is determined by mapping a general vector to the vector
where is the conjugate of , and the product is Clifford multiplication. In this situation, a spinor is an ordinary complex number. The action of on a spinor is given by ordinary complex multiplication:
An important feature of this definition is the distinction between ordinary vectors and spinors, manifested in how the even-graded elements act on each of them in different ways. In general, a quick check of the Clifford relations reveals that even-graded elements conjugate-commute with ordinary vectors:
On the other hand, in comparison with its action on spinors , the action of on ordinary vectors appears as the ''square'' of its action on spinors.
Consider, for example, the implication this has for plane rotations. Rotating a vector through an angle of ''θ'' corresponds to , so that the corresponding action on spinors is via . In general, because of logarithmic branching, it is impossible to choose a sign in a consistent way. Thus the representation of plane rotations on spinors is two-valued.
In applications of spinors in two dimensions, it is common to exploit the fact that the algebra of even-graded elements (that is just the ring of complex numbers) is identical to the space of spinors. So, by abuse of language, the two are often conflated. One may then talk about "the action of a spinor on a vector". In a general setting, such statements are meaningless. But in dimensions 2 and 3 (as applied, for example, to computer graphics
Computer graphics deals with generating images and art with the aid of computers. Computer graphics is a core technology in digital photography, film, video games, digital art, cell phone and computer displays, and many specialized applications. ...
) they make sense.
Examples
* The even-graded element corresponds to a vector rotation of 90° from ''σ''1 around towards ''σ''2, which can be checked by confirming that It corresponds to a spinor rotation of only 45°, however: * Similarly the even-graded element corresponds to a vector rotation of 180°: but a spinor rotation of only 90°: * Continuing on further, the even-graded element corresponds to a vector rotation of 360°: but a spinor rotation of 180°.Three dimensions
The Clifford algebra Cℓ3,0() is built up from a basis of one unit scalar, 1, three orthogonal unit vectors, ''σ''1, ''σ''2 and ''σ''3, the three unit bivectors ''σ''1''σ''2, ''σ''2''σ''3, ''σ''3''σ''1 and thepseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
A pseudoscalar, when multiplied by an ordinary vector, becomes a '' pseudovector'' ...
. It is straightforward to show that , and .
The sub-algebra of even-graded elements is made up of scalar dilations,
and vector rotations
where
}
corresponds to a vector rotation through an angle ''θ'' about an axis defined by a unit vector .
As a special case, it is easy to see that, if , this reproduces the ''σ''1''σ''2 rotation considered in the previous section; and that such rotation leaves the coefficients of vectors in the ''σ''3 direction invariant, since
The bivectors ''σ''2''σ''3, ''σ''3''σ''1 and ''σ''1''σ''2 are in fact Hamilton's quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s i, j, and k, discovered in 1843:
With the identification of the even-graded elements with the algebra of quaternions, as in the case of two dimensions the only representation of the algebra of even-graded elements is on itself. Thus the (real) spinors in three-dimensions are quaternions, and the action of an even-graded element on a spinor is given by ordinary quaternionic multiplication.
Note that the expression (1) for a vector rotation through an angle , ''the angle appearing in γ was halved''. Thus the spinor rotation (ordinary quaternionic multiplication) will rotate the spinor through an angle one-half the measure of the angle of the corresponding vector rotation. Once again, the problem of lifting a vector rotation to a spinor rotation is two-valued: the expression (1) with in place of ''θ''/2 will produce the same vector rotation, but the negative of the spinor rotation.
The spinor/quaternion representation of rotations in 3D is becoming increasingly prevalent in computer geometry and other applications, because of the notable brevity of the corresponding spin matrix, and the simplicity with which they can be multiplied together to calculate the combined effect of successive rotations about different axes.
Explicit constructions
A space of spinors can be constructed explicitly with concrete and abstract constructions. The equivalence of these constructions is a consequence of the uniqueness of the spinor representation of the complex Clifford algebra. For a complete example in dimension 3, see spinors in three dimensions.Component spinors
Given a vector space ''V'' and a quadratic form ''g'' an explicit matrix representation of the Clifford algebra can be defined as follows. Choose an orthonormal basis for ''V'' i.e. where and for . Let . Fix a set of matrices such that (i.e. fix a convention for thegamma matrices
In mathematical physics, the gamma matrices, \ \left\\ , also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra \ \mathr ...
). Then the assignment extends uniquely to an algebra homomorphism by sending the monomial in the Clifford algebra to the product of matrices and extending linearly. The space on which the gamma matrices act is now a space of spinors. One needs to construct such matrices explicitly, however. In dimension 3, defining the gamma matrices to be the Pauli sigma matrices gives rise to the familiar two component spinors used in non relativistic quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
. Likewise using the Dirac gamma matrices gives rise to the 4 component Dirac spinors used in 3+1 dimensional relativistic quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct phy ...
. In general, in order to define gamma matrices of the required kind, one can use the Weyl–Brauer matrices.
In this construction the representation of the Clifford algebra , the Lie algebra , and the Spin group , all depend on the choice of the orthonormal basis and the choice of the gamma matrices. This can cause confusion over conventions, but invariants like traces are independent of choices. In particular, all physically observable quantities must be independent of such choices. In this construction a spinor can be represented as a vector of 2''k'' complex numbers and is denoted with spinor indices (usually ''α'', ''β'', ''γ''). In the physics literature, such indices are often used to denote spinors even when an abstract spinor construction is used.
Abstract spinors
There are at least two different, but essentially equivalent, ways to define spinors abstractly. One approach seeks to identify the minimal ideals for the left action of on itself. These are subspaces of the Clifford algebra of the form , admitting the evident action of by left-multiplication: . There are two variations on this theme: one can either find a primitive element that is anilpotent
In mathematics, an element x of a ring (mathematics), ring R is called nilpotent if there exists some positive integer n, called the index (or sometimes the degree), such that x^n=0.
The term, along with its sister Idempotent (ring theory), idem ...
element of the Clifford algebra, or one that is an idempotent
Idempotence (, ) is the property of certain operations in mathematics and computer science whereby they can be applied multiple times without changing the result beyond the initial application. The concept of idempotence arises in a number of pl ...
. The construction via nilpotent elements is more fundamental in the sense that an idempotent may then be produced from it. In this way, the spinor representations are identified with certain subspaces of the Clifford algebra itself. The second approach is to construct a vector space using a distinguished subspace of , and then specify the action of the Clifford algebra ''externally'' to that vector space.
In either approach, the fundamental notion is that of an isotropic subspace . Each construction depends on an initial freedom in choosing this subspace. In physical terms, this corresponds to the fact that there is no measurement protocol that can specify a basis of the spin space, even if a preferred basis of is given.
As above, we let be an -dimensional complex vector space equipped with a nondegenerate bilinear form. If is a real vector space, then we replace by its complexification and let denote the induced bilinear form on . Let be a maximal isotropic subspace, i.e. a maximal subspace of such that . If is even, then let be an isotropic subspace complementary to . If is odd, let be a maximal isotropic subspace with , and let be the orthogonal complement of . In both the even- and odd-dimensional cases and have dimension . In the odd-dimensional case, is one-dimensional, spanned by a unit vector .
Minimal ideals
Since ''W'' is isotropic, multiplication of elements of ''W'' inside is skew. Hence vectors in ''W'' anti-commute, and is just theexterior algebra
In mathematics, the exterior algebra or Grassmann algebra of a vector space V is an associative algebra that contains V, which has a product, called exterior product or wedge product and denoted with \wedge, such that v\wedge v=0 for every vector ...
Λ∗''W''. Consequently, the ''k''-fold product of ''W'' with itself, ''W''''k'', is one-dimensional. Let ''ω'' be a generator of ''W''''k''. In terms of a basis of in ''W'', one possibility is to set
Note that (i.e., ''ω'' is nilpotent of order 2), and moreover, for all . The following facts can be proven easily:
# If , then the left ideal is a minimal left ideal. Furthermore, this splits into the two spin spaces and on restriction to the action of the even Clifford algebra.
# If , then the action of the unit vector ''u'' on the left ideal decomposes the space into a pair of isomorphic irreducible eigenspaces (both denoted by Δ), corresponding to the respective eigenvalues +1 and −1.
In detail, suppose for instance that ''n'' is even. Suppose that ''I'' is a non-zero left ideal contained in . We shall show that ''I'' must be equal to by proving that it contains a nonzero scalar multiple of ''ω''.
Fix a basis ''w''''i'' of ''W'' and a complementary basis ''w''''i''′ of ''W'' so that
Note that any element of ''I'' must have the form ''αω'', by virtue of our assumption that . Let be any such element. Using the chosen basis, we may write
where the ''a''''i''1...''i''''p'' are scalars, and the ''B''''j'' are auxiliary elements of the Clifford algebra. Observe now that the product
Pick any nonzero monomial ''a'' in the expansion of ''α'' with maximal homogeneous degree in the elements ''w''i:
(no summation implied),
then
is a nonzero scalar multiple of ''ω'', as required.
Note that for ''n'' even, this computation also shows that
as a vector space. In the last equality we again used that ''W'' is isotropic. In physics terms, this shows that Δ is built up like a Fock space by creating spinors using anti-commuting creation operators in ''W'' acting on a vacuum ''ω''.
Exterior algebra construction
The computations with the minimal ideal construction suggest that a spinor representation can also be defined directly using theexterior algebra
In mathematics, the exterior algebra or Grassmann algebra of a vector space V is an associative algebra that contains V, which has a product, called exterior product or wedge product and denoted with \wedge, such that v\wedge v=0 for every vector ...
of the isotropic subspace ''W''.
Let denote the exterior algebra of ''W'' considered as vector space only. This will be the spin representation, and its elements will be referred to as spinors.
The action of the Clifford algebra on Δ is defined first by giving the action of an element of ''V'' on Δ, and then showing that this action respects the Clifford relation and so extends to a homomorphism
In algebra, a homomorphism is a morphism, structure-preserving map (mathematics), map between two algebraic structures of the same type (such as two group (mathematics), groups, two ring (mathematics), rings, or two vector spaces). The word ''homo ...
of the full Clifford algebra into the endomorphism ring
In mathematics, the endomorphisms of an abelian group ''X'' form a ring. This ring is called the endomorphism ring of ''X'', denoted by End(''X''); the set of all homomorphisms of ''X'' into itself. Addition of endomorphisms arises naturally in ...
End(Δ) by the universal property of Clifford algebras. The details differ slightly according to whether the dimension of ''V'' is even or odd.
When dim() is even, where ''W'' is the chosen isotropic complement. Hence any decomposes uniquely as with and . The action of on a spinor is given by
where ''i''(''w'') is interior product
In mathematics, the interior product (also known as interior derivative, interior multiplication, inner multiplication, inner derivative, insertion operator, contraction, or inner derivation) is a degree −1 (anti)derivation on the exterio ...
with ''w'' using the nondegenerate quadratic form to identify ''V'' with ''V''∗, and ''ε''(''w'') denotes the exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of ...
. This action is sometimes called the Clifford product. It may be verified that
and so respects the Clifford relations and extends to a homomorphism from the Clifford algebra to End(Δ).
The spin representation Δ further decomposes into a pair of irreducible complex representations of the Spin group (the half-spin representations, or Weyl spinors) via
When dim(''V'') is odd, , where ''U'' is spanned by a unit vector ''u'' orthogonal to ''W''. The Clifford action ''c'' is defined as before on , while the Clifford action of (multiples of) ''u'' is defined by
As before, one verifies that ''c'' respects the Clifford relations, and so induces a homomorphism.
Hermitian vector spaces and spinors
If the vector space ''V'' has extra structure that provides a decomposition of its complexification into two maximal isotropic subspaces, then the definition of spinors (by either method) becomes natural. The main example is the case that the real vector space ''V'' is a hermitian vector space , i.e., ''V'' is equipped with a complex structure ''J'' that is anorthogonal transformation
In linear algebra, an orthogonal transformation is a linear transformation ''T'' : ''V'' → ''V'' on a real inner product space ''V'', that preserves the inner product. That is, for each pair of elements of ''V'', we hav ...
with respect to the inner product ''g'' on ''V''. Then splits in the eigenspaces of ''J''. These eigenspaces are isotropic for the complexification of ''g'' and can be identified with the complex vector space and its complex conjugate . Therefore, for a hermitian vector space the vector space (as well as its complex conjugate ) is a spinor space for the underlying real euclidean vector space.
With the Clifford action as above but with contraction using the hermitian form, this construction gives a spinor space at every point of an almost Hermitian manifold and is the reason why every almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with a smooth linear complex structure on each tangent space. Every complex manifold is an almost complex manifold, but there are almost complex manifolds that are not comple ...
(in particular every symplectic manifold
In differential geometry, a subject of mathematics, a symplectic manifold is a smooth manifold, M , equipped with a closed nondegenerate differential 2-form \omega , called the symplectic form. The study of symplectic manifolds is called sy ...
) has a Spinc structure. Likewise, every complex vector bundle on a manifold carries a Spinc structure.
Clebsch–Gordan decomposition
A number of Clebsch–Gordan decompositions are possible on thetensor product
In mathematics, the tensor product V \otimes W of two vector spaces V and W (over the same field) is a vector space to which is associated a bilinear map V\times W \rightarrow V\otimes W that maps a pair (v,w),\ v\in V, w\in W to an element of ...
of one spin representation with another.. These decompositions express the tensor product in terms of the alternating representations of the orthogonal group.
For the real or complex case, the alternating representations are
* , the representation of the orthogonal group on skew tensors of rank ''r''.
In addition, for the real orthogonal groups, there are three characters (one-dimensional representations)
* ''σ''+ : O(''p'', ''q'') → given by , if ''R'' reverses the spatial orientation of ''V'', +1, if ''R'' preserves the spatial orientation of ''V''. (''The spatial character''.)
* ''σ''− : O(''p'', ''q'') → given by , if ''R'' reverses the temporal orientation of ''V'', +1, if ''R'' preserves the temporal orientation of ''V''. (''The temporal character''.)
* ''σ'' = ''σ''+''σ''− . (''The orientation character''.)
The Clebsch–Gordan decomposition allows one to define, among other things:
* An action of spinors on vectors.
* A Hermitian metric
In mathematics, and more specifically in differential geometry, a Hermitian manifold is the complex analogue of a Riemannian manifold
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as ...
on the complex representations of the real spin groups.
* A Dirac operator
In mathematics and in quantum mechanics, a Dirac operator is a first-order differential operator that is a formal square root, or half-iterate, of a second-order differential operator such as a Laplacian. It was introduced in 1847 by William Ham ...
on each spin representation.
Even dimensions
If is even, then the tensor product of Δ with the contragredient representation decomposes as which can be seen explicitly by considering (in the Explicit construction) the action of the Clifford algebra on decomposable elements . The rightmost formulation follows from the transformation properties of theHodge star operator
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a Dimension (vector space), finite-dimensional orientation (vector space), oriented vector space endowed with a Degenerate bilinear form, nonde ...
. Note that on restriction to the even Clifford algebra, the paired summands are isomorphic, but under the full Clifford algebra they are not.
There is a natural identification of Δ with its contragredient representation via the conjugation in the Clifford algebra:
So also decomposes in the above manner. Furthermore, under the even Clifford algebra, the half-spin representations decompose
For the complex representations of the real Clifford algebras, the associated reality structure on the complex Clifford algebra descends to the space of spinors (via the explicit construction in terms of minimal ideals, for instance). In this way, we obtain the complex conjugate of the representation Δ, and the following isomorphism is seen to hold:
In particular, note that the representation Δ of the orthochronous spin group is a unitary representation
In mathematics, a unitary representation of a group ''G'' is a linear representation π of ''G'' on a complex Hilbert space ''V'' such that π(''g'') is a unitary operator for every ''g'' ∈ ''G''. The general theory is well-developed in the ca ...
. In general, there are Clebsch–Gordan decompositions
In metric signature , the following isomorphisms hold for the conjugate half-spin representations
* If ''q'' is even, then and
* If ''q'' is odd, then and
Using these isomorphisms, one can deduce analogous decompositions for the tensor products of the half-spin representations .
Odd dimensions
If is odd, then In the real case, once again the isomorphism holds Hence there is a Clebsch–Gordan decomposition (again using the Hodge star to dualize) given byConsequences
There are many far-reaching consequences of the Clebsch–Gordan decompositions of the spinor spaces. The most fundamental of these pertain to Dirac's theory of the electron, among whose basic requirements are * A manner of regarding the product of two spinors ''ψ'' as a scalar. In physical terms, a spinor should determine aprobability amplitude
In quantum mechanics, a probability amplitude is a complex number used for describing the behaviour of systems. The square of the modulus of this quantity at a point in space represents a probability density at that point.
Probability amplitu ...
for the quantum state
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system ...
.
* A manner of regarding the product ''ψ'' as a vector. This is an essential feature of Dirac's theory, which ties the spinor formalism to the geometry of physical space.
* A manner of regarding a spinor as acting upon a vector, by an expression such as ''ψv''. In physical terms, this represents an electric current
An electric current is a flow of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is defined as the net rate of flow of electric charge through a surface. The moving particles are called charge c ...
of Maxwell's electromagnetic theory
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interact ...
, or more generally a probability current.
Summary in low dimensions
* In 1 dimension (a trivial example), the single spinor representation is formally Majorana, a real 1-dimensional representation that does not transform. * In 2 Euclidean dimensions, the left-handed and the right-handed Weyl spinor are 1-componentcomplex representation
In mathematics, a complex representation is a representation of a group (or that of Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bil ...
s, i.e. complex numbers that get multiplied by ''e''±''iφ''/2 under a rotation by angle ''φ''.
* In 3 Euclidean dimensions, the single spinor representation is 2-dimensional and quaternionic
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions ...
. The existence of spinors in 3 dimensions follows from the isomorphism of the groups that allows us to define the action of Spin(3) on a complex 2-component column (a spinor); the generators of SU(2) can be written as Pauli matrices
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () ...
.
* In 4 Euclidean dimensions, the corresponding isomorphism is . There are two inequivalent quaternionic
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions ...
2-component Weyl spinors and each of them transforms under one of the SU(2) factors only.
* In 5 Euclidean dimensions, the relevant isomorphism is that implies that the single spinor representation is 4-dimensional and quaternionic.
* In 6 Euclidean dimensions, the isomorphism guarantees that there are two 4-dimensional complex Weyl representations that are complex conjugates of one another.
* In 7 Euclidean dimensions, the single spinor representation is 8-dimensional and real; no isomorphisms to a Lie algebra from another series (A or C) exist from this dimension on.
* In 8 Euclidean dimensions, there are two Weyl–Majorana real 8-dimensional representations that are related to the 8-dimensional real vector representation by a special property of Spin(8) called triality.
* In dimensions, the number of distinct irreducible spinor representations and their reality (whether they are real, pseudoreal, or complex) mimics the structure in ''d'' dimensions, but their dimensions are 16 times larger; this allows one to understand all remaining cases. See Bott periodicity.
* In spacetimes with ''p'' spatial and ''q'' time-like directions, the dimensions viewed as dimensions over the complex numbers coincide with the case of the -dimensional Euclidean space, but the reality projections mimic the structure in Euclidean dimensions. For example, in dimensions there are two non-equivalent Weyl complex (like in 2 dimensions) 2-component (like in 4 dimensions) spinors, which follows from the isomorphism .
See also
*Anyon
In physics, an anyon is a type of quasiparticle so far observed only in two-dimensional physical system, systems. In three-dimensional systems, only two kinds of elementary particles are seen: fermions and bosons. Anyons have statistical proper ...
* Dirac equation in the algebra of physical space
* Eigenspinor
* Einstein–Cartan theory
* Projective representation
In the field of representation theory in mathematics, a projective representation of a group ''G'' on a vector space ''V'' over a field ''F'' is a group homomorphism from ''G'' to the projective linear group
\mathrm(V) = \mathrm(V) / F^*,
where G ...
* Pure spinor
* Spin-1/2
In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of . The spin number describes how many symmetrical facets a particle has in one f ...
* Spinor bundle
In differential geometry, given a spin structure on an n-dimensional orientable Riemannian manifold (M, g),\, one defines the spinor bundle to be the complex vector bundle \pi_\colon\to M\, associated to the corresponding principal bundle \pi_\co ...
* Supercharge
In theoretical physics, a supercharge is a generator of supersymmetry transformations. It is an example of the general notion of a charge (physics), charge in physics.
Supercharge, denoted by the symbol Q, is an operator which transforms bosons in ...
* Twistor theory
In theoretical physics, twistor theory was proposed by Roger Penrose in 1967 as a possible path to quantum gravity and has evolved into a widely studied branch of theoretical and mathematical physics. Penrose's idea was that twistor space should ...
* Spacetime algebra
In mathematical physics, spacetime algebra (STA) is the application of Clifford algebra Cl1,3(R), or equivalently the geometric algebra to physics. Spacetime algebra provides a "unified, coordinate-free formulation for all of special relativity, ...
Notes
References
Works cited
* * * * * * * *Further reading
* * * * * {{tensors Rotation in three dimensions Quantum mechanics Quantum field theory