right trapezoid on:
[Wikipedia]
[Google]
[Amazon]
A quadrilateral with at least one pair of parallel sides is called a trapezoid () in American and Canadian English. In British and other forms of English, it is called a trapezium ().
A trapezoid is necessarily a
 Ancient Greek mathematician
Ancient Greek mathematician
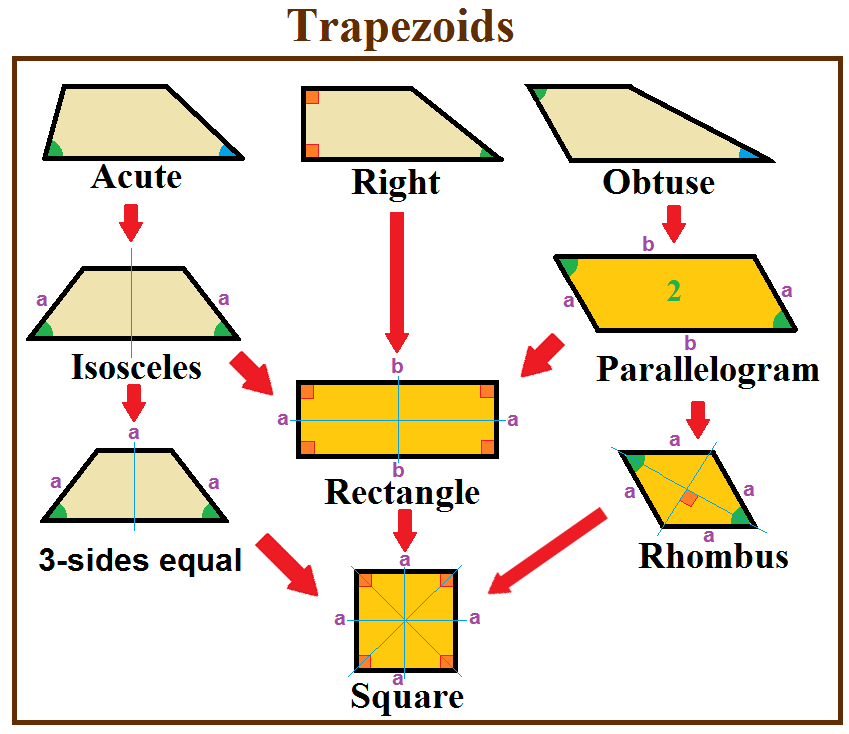 A right trapezoid (also called ''right-angled trapezoid'') has two adjacent
A right trapezoid (also called ''right-angled trapezoid'') has two adjacent
 Given a convex quadrilateral, the following properties are equivalent, and each implies that the quadrilateral is a trapezoid:
*It has two adjacent
Given a convex quadrilateral, the following properties are equivalent, and each implies that the quadrilateral is a trapezoid:
*It has two adjacent
"Characterizations of trapezoids"
Forum Geometricorum, 13 (2013) 23-35. *The product of the areas of the two triangles formed by one diagonal equals the product of the areas of the two triangles formed by the other diagonal. *The areas ''S'' and ''T'' of some two opposite triangles of the four triangles formed by the diagonals satisfy the equation :: :where ''K'' is the area of the quadrilateral. *The midpoints of two opposite sides and the intersection of the diagonals are
 The lengths of the diagonals are
:
:
where ''a'' is the short base, ''b'' is the long base, and ''c'' and ''d'' are the trapezoid legs.
If the trapezoid is divided into four triangles by its diagonals ''AC'' and ''BD'' (as shown on the right), intersecting at ''O'', then the area of is equal to that of , and the product of the areas of and is equal to that of and . The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides.
Let the trapezoid have vertices ''A'', ''B'', ''C'', and ''D'' in sequence and have parallel sides ''AB'' and ''DC''. Let ''E'' be the intersection of the diagonals, and let ''F'' be on side ''DA'' and ''G'' be on side ''BC'' such that ''FEG'' is parallel to ''AB'' and ''CD''. Then ''FG'' is the
The lengths of the diagonals are
:
:
where ''a'' is the short base, ''b'' is the long base, and ''c'' and ''d'' are the trapezoid legs.
If the trapezoid is divided into four triangles by its diagonals ''AC'' and ''BD'' (as shown on the right), intersecting at ''O'', then the area of is equal to that of , and the product of the areas of and is equal to that of and . The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides.
Let the trapezoid have vertices ''A'', ''B'', ''C'', and ''D'' in sequence and have parallel sides ''AB'' and ''DC''. Let ''E'' be the intersection of the diagonals, and let ''F'' be on side ''DA'' and ''G'' be on side ''BC'' such that ''FEG'' is parallel to ''AB'' and ''CD''. Then ''FG'' is the
Methods for Euclidean Geometry
', Mathematical Association of America, 2010, p. 55. :
 In
In
''Common properties of trapezoids and convex quadrilaterals''
"Trapezium"
at ''
Trapezoid definition
With interactive animations
Trapezoid (North America)
at elsy.at: Animated course (construction, circumference, area)
on ''Numerical Methods for Stem Undergraduate'' * Autar Kaw and E. Eric Kalu,
', (2008) {{Polygons Elementary shapes Types of quadrilaterals
convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytope ...
quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
in Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' (or the ''lateral sides'') if they are not parallel; otherwise, the trapezoid is a parallelogram, and there are two pairs of bases). A ''scalene trapezoid'' is a trapezoid with no sides of equal measure, in contrast with the special cases
Special or specials may refer to:
Policing
* Specials, Ulster Special Constabulary, the Northern Ireland police force
* Specials, Special Constable, an auxiliary, volunteer, or temporary; police worker or police officer
Literature
* ''Specia ...
below.
Etymology and ''trapezium'' versus ''trapezoid''
 Ancient Greek mathematician
Ancient Greek mathematician Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
defined five types of quadrilateral, of which four had two sets of parallel sides (known in English as square, rectangle, rhombus and rhomboid) and the last did not have two sets of parallel sides – a τραπέζια (''trapezia'' literally "a table", itself from τετράς (''tetrás''), "four" + πέζα (''péza''), "a foot; end, border, edge").
Two types of ''trapezia'' were introduced by Proclus
Proclus Lycius (; 8 February 412 – 17 April 485), called Proclus the Successor ( grc-gre, Πρόκλος ὁ Διάδοχος, ''Próklos ho Diádokhos''), was a Greek Neoplatonist philosopher, one of the last major classical philosophers ...
(412 to 485 AD) in his commentary on the first book of Euclid's Elements
The ''Elements'' ( grc, Στοιχεῖα ''Stoikheîa'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postulat ...
:
* one pair of parallel sides – a ''trapezium'' (τραπέζιον), divided into isosceles (equal legs) and scalene (unequal) trapezia
* no parallel sides – ''trapezoid'' (τραπεζοειδή, ''trapezoeidé'', literally trapezium-like ( εἶδος means "resembles"), in the same way as cuboid
In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube", in the sense that by adjusting the length of the edges or the angles between edges and faces a cuboid can be transformed into a cub ...
means cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
-like and rhomboid
Traditionally, in two-dimensional geometry, a rhomboid is a parallelogram in which adjacent sides are of unequal lengths and angles are non-right angled.
A parallelogram with sides of equal length (equilateral) is a rhombus but not a rhomboid.
...
means rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The ...
-like)
All European languages follow Proclus's structure as did English until the late 18th century, until an influential mathematical dictionary published by Charles Hutton
Charles Hutton FRS FRSE LLD (14 August 1737 – 27 January 1823) was a British mathematician and surveyor. He was professor of mathematics at the Royal Military Academy, Woolwich from 1773 to 1807. He is remembered for his calculation of th ...
in 1795 supported without explanation a transposition of the terms. This mistake was corrected in British English in about 1875, but was retained in American English into the modern day.
The following is a table comparing usages, with the most specific definitions at the top to the most general at the bottom.
Inclusive vs exclusive definition
There is some disagreement whetherparallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
s, which have two pairs of parallel sides, should be regarded as trapezoids. Some define a trapezoid as a quadrilateral having ''only'' one pair of parallel sides (the exclusive definition), thereby excluding parallelograms. Others define a trapezoid as a quadrilateral with ''at least'' one pair of parallel sides (the inclusive definition), making the parallelogram a special type of trapezoid. The latter definition is consistent with its uses in higher mathematics such as calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
. This article uses the inclusive definition and considers parallelograms as special cases of a trapezoid. This is also advocated in the taxonomy of quadrilaterals.
Under the inclusive definition, all parallelograms (including rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The ...
es, square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
s and non-square rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
s) are trapezoids. Rectangles have mirror symmetry on mid-edges; rhombuses have mirror symmetry on vertices, while squares have mirror symmetry on both mid-edges and vertices.
Special cases
 A right trapezoid (also called ''right-angled trapezoid'') has two adjacent
A right trapezoid (also called ''right-angled trapezoid'') has two adjacent right angles
In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or radians corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. T ...
. Right trapezoids are used in the trapezoidal rule
In calculus, the trapezoidal rule (also known as the trapezoid rule or trapezium rule; see Trapezoid for more information on terminology) is a technique for approximating the definite integral.
\int_a^b f(x) \, dx.
The trapezoidal rule works b ...
for estimating areas under a curve.
An acute trapezoid has two adjacent acute angles on its longer ''base'' edge, while an obtuse trapezoid has one acute and one obtuse angle on each ''base''.
An isosceles trapezoid
In Euclidean geometry, an isosceles trapezoid (isosceles trapezium in British English) is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined ...
is a trapezoid where the base angles have the same measure. As a consequence the two legs are also of equal length and it has reflection symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.
In 2D ther ...
. This is possible for acute trapezoids or right trapezoids (rectangles).
A parallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
is a trapezoid with two pairs of parallel sides. A parallelogram has central 2-fold rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which i ...
(or point reflection
In geometry, a point reflection (point inversion, central inversion, or inversion through a point) is a type of isometry of Euclidean space. An object that is invariant under a point reflection is said to possess point symmetry; if it is invari ...
symmetry). It is possible for obtuse trapezoids or right trapezoids (rectangles).
A tangential trapezoid
In Euclidean geometry, a tangential trapezoid, also called a circumscribed trapezoid, is a trapezoid whose four sides are all tangent to a circle within the trapezoid: the incircle or ''inscribed circle''. It is the special case of a tangential ...
is a trapezoid that has an incircle
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter.
...
.
A Saccheri quadrilateral
A Saccheri quadrilateral (also known as a Khayyam–Saccheri quadrilateral) is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book ''Euclides ab omni na ...
is similar to a trapezoid in the hyperbolic plane, with two adjacent right angles, while it is a rectangle in the Euclidean plane. A Lambert quadrilateral
In geometry, a Lambert quadrilateral (also known as Ibn al-Haytham–Lambert quadrilateral), is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest s ...
in the hyperbolic plane has 3 right angles.
Condition of existence
Four lengths ''a'', ''c'', ''b'', ''d'' can constitute the consecutive sides of a non-parallelogram trapezoid with ''a'' and ''b'' parallel only when : The quadrilateral is a parallelogram when , but it is anex-tangential quadrilateral
In Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the ''extensions'' of all four sides are tangent to a circle outside the quadrilateral.Radic, Mirko; Kaliman, Zoran and Kadum, Vladimir, "A condition that a tan ...
(which is not a trapezoid) when .
Characterizations
angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle.
Angles formed by two ...
s that are supplementary, that is, they add up to 180 degree
Degree may refer to:
As a unit of measurement
* Degree (angle), a unit of angle measurement
** Degree of geographical latitude
** Degree of geographical longitude
* Degree symbol (°), a notation used in science, engineering, and mathematics
...
s.
*The angle between a side and a diagonal is equal to the angle between the opposite side and the same diagonal.
*The diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek δ ...
s cut each other in mutually the same ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
(this ratio is the same as that between the lengths of the parallel sides).
*The diagonals cut the quadrilateral into four triangles of which one opposite pair have equal areas.Martin Josefsson"Characterizations of trapezoids"
Forum Geometricorum, 13 (2013) 23-35. *The product of the areas of the two triangles formed by one diagonal equals the product of the areas of the two triangles formed by the other diagonal. *The areas ''S'' and ''T'' of some two opposite triangles of the four triangles formed by the diagonals satisfy the equation :: :where ''K'' is the area of the quadrilateral. *The midpoints of two opposite sides and the intersection of the diagonals are
collinear
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, the term has been used for aligned ...
.
*The angles in the quadrilateral ''ABCD'' satisfy
*The cosines of two adjacent angles sum to 0, as do the cosines of the other two angles.
*The cotangents of two adjacent angles sum to 0, as do the cotangents of the other two adjacent angles.
*One bimedian divides the quadrilateral into two quadrilaterals of equal areas.
*Twice the length of the bimedian connecting the midpoints of two opposite sides equals the sum of the lengths of the other sides.
Additionally, the following properties are equivalent, and each implies that opposite sides ''a'' and ''b'' are parallel:
* The consecutive sides ''a'', ''c'', ''b'', ''d'' and the diagonals ''p'', ''q'' satisfy the equation
::
*The distance ''v'' between the midpoints of the diagonals satisfies the equation
::
Midsegment and height
The ''midsegment'' (also called the median or midline) of a trapezoid is the segment that joins themidpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dimens ...
s of the legs. It is parallel to the bases. Its length ''m'' is equal to the average of the lengths of the bases ''a'' and ''b'' of the trapezoid,
:
The midsegment of a trapezoid is one of the two bimedian
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
s (the other bimedian divides the trapezoid into equal areas).
The ''height'' (or altitude) is the perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can ...
distance between the bases. In the case that the two bases have different lengths (''a'' ≠ ''b''), the height of a trapezoid ''h'' can be determined by the length of its four sides using the formula
:
where ''c'' and ''d'' are the lengths of the legs.
Area
The area ''K'' of a trapezoid is given by : where ''a'' and ''b'' are the lengths of the parallel sides, ''h'' is the height (the perpendicular distance between these sides), and ''m'' is thearithmetic mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The colle ...
of the lengths of the two parallel sides. In 499 AD Aryabhata
Aryabhata (ISO: ) or Aryabhata I (476–550 CE) was an Indian mathematician and astronomer of the classical age of Indian mathematics and Indian astronomy. He flourished in the Gupta Era and produced works such as the ''Aryabhatiya'' (which ...
, a great mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
History
On ...
-astronomer
An astronomer is a scientist in the field of astronomy who focuses their studies on a specific question or field outside the scope of Earth. They observe astronomical objects such as stars, planets, natural satellite, moons, comets and galaxy, g ...
from the classical age of Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta ...
and Indian astronomy
Astronomy has long history in Indian subcontinent stretching from pre-historic to modern times. Some of the earliest roots of Indian astronomy can be dated to the period of Indus Valley civilisation or earlier. Astronomy later developed as a dis ...
, used this method in the ''Aryabhatiya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Sanskrit astronomical treatise, is the ''magnum opus'' and only known surviving work of the 5th century Indian mathematician Aryabhata. Philosopher of astronomy Roger Billard estimates that th ...
'' (section 2.8). This yields as a special case
In logic, especially as applied in mathematics, concept is a special case or specialization of concept precisely if every instance of is also an instance of but not vice versa, or equivalently, if is a generalization of . A limiting case is ...
the well-known formula for the area of a triangle
A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, an ...
, by considering a triangle as a degenerate trapezoid in which one of the parallel sides has shrunk to a point.
The 7th-century Indian mathematician Bhāskara I
Bhāskara () (commonly called Bhāskara I to avoid confusion with the 12th-century mathematician Bhāskara II) was a 7th-century Indian mathematician and astronomer who was the first to write numbers in the Hindu–Arabic decimal system with a ...
derived the following formula for the area of a trapezoid with consecutive sides ''a'', ''c'', ''b'', ''d'':
:
where ''a'' and ''b'' are parallel and ''b'' > ''a''. This formula can be factored into a more symmetric version
:
When one of the parallel sides has shrunk to a point (say ''a'' = 0), this formula reduces to Heron's formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths , , . If s = \tfrac12(a + b + c) is the semiperimeter of the triangle, the area is,
:A = \sqrt.
It is named after first-century ...
for the area of a triangle.
Another equivalent formula for the area, which more closely resembles Heron's formula, is
:
:
where is the semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name ...
of the trapezoid. (This formula is similar to Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula is used to find the area of any cyclic quadrilateral (one that can be inscribed in a circle) given the lengths of the sides; its generalized version (Bretschneider's formula) can be used with non-cyclic ...
, but it differs from it, in that a trapezoid might not be cyclic
Cycle, cycles, or cyclic may refer to:
Anthropology and social sciences
* Cyclic history, a theory of history
* Cyclical theory, a theory of American political history associated with Arthur Schlesinger, Sr.
* Social cycle, various cycles in soc ...
(inscribed in a circle). The formula is also a special case of Bretschneider's formula
In geometry, Bretschneider's formula is the following expression for the area of a general quadrilateral:
: K = \sqrt
::= \sqrt .
Here, , , , are the sides of the quadrilateral, is the semiperimeter, and and are any two opposite angles, sinc ...
for a general quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
).
From Bretschneider's formula, it follows that
:
The line that joins the midpoints of the parallel sides, bisects the area.
Diagonals
harmonic mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired.
The harmonic mean can be expressed as the recipro ...
of ''AB'' and ''DC'':
:
The line that goes through both the intersection point of the extended nonparallel sides and the intersection point of the diagonals, bisects each base.
Other properties
The center of area (center of mass for a uniformlamina
Lamina may refer to:
Science and technology
* Planar lamina, a two-dimensional planar closed surface with mass and density, in mathematics
* Laminar flow, (or streamline flow) occurs when a fluid flows in parallel layers, with no disruption betwee ...
) lies along the line segment joining the midpoints of the parallel sides, at a perpendicular distance ''x'' from the longer side ''b'' given by
:
The center of area divides this segment in the ratio (when taken from the short to the long side)
:
If the angle bisectors to angles ''A'' and ''B'' intersect at ''P'', and the angle bisectors to angles ''C'' and ''D'' intersect at ''Q'', thenOwen Byer, Felix Lazebnik and Deirdre Smeltzer
Deirdre Longacher Smeltzer (born 1964) is an American mathematician, mathematics educator, textbook author, and academic administrator. A former professor, dean, and vice president at Eastern Mennonite University, she is Senior Director for Prog ...
, Methods for Euclidean Geometry
', Mathematical Association of America, 2010, p. 55. :
Applications
Architecture
In architecture the word is used to refer to symmetrical doors, windows, and buildings built wider at the base, tapering toward the top, in Egyptian style. If these have straight sides and sharp angular corners, their shapes are usuallyisosceles trapezoid
In Euclidean geometry, an isosceles trapezoid (isosceles trapezium in British English) is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined ...
s. This was the standard style for the doors and windows of the Inca
The Inca Empire (also known as the Incan Empire and the Inka Empire), called ''Tawantinsuyu'' by its subjects, (Quechua for the "Realm of the Four Parts", "four parts together" ) was the largest empire in pre-Columbian America. The admin ...
.
Geometry
Thecrossed ladders problem The crossed ladders problem is a puzzle of unknown origin that has appeared in various publications and regularly reappears in Web pages and Usenet discussions.
The problem
Two ladders of lengths ''a'' and ''b'' lie oppositely across an alley, a ...
is the problem of finding the distance between the parallel sides of a right trapezoid, given the diagonal lengths and the distance from the perpendicular leg to the diagonal intersection.
Biology
 In
In morphology
Morphology, from the Greek and meaning "study of shape", may refer to:
Disciplines
*Morphology (archaeology), study of the shapes or forms of artifacts
*Morphology (astronomy), study of the shape of astronomical objects such as nebulae, galaxies, ...
, taxonomy
Taxonomy is the practice and science of categorization or classification.
A taxonomy (or taxonomical classification) is a scheme of classification, especially a hierarchical classification, in which things are organized into groups or types. ...
and other descriptive disciplines in which a term for such shapes is necessary, terms such as ''trapezoidal'' or ''trapeziform'' commonly are useful in descriptions of particular organs or forms.
Computer engineering
In computer engineering, specifically digital logic and computer architecture, trapezoids are typically utilized to symbolize multiplexors. Multiplexors are logic elements that select between multiple elements and produce a single output based on a select signal. Typical designs will employ trapezoids without specifically stating they are multiplexors as they are universally equivalent.See also
*Frustum
In geometry, a (from the Latin for "morsel"; plural: ''frusta'' or ''frustums'') is the portion of a solid (normally a pyramid or a cone) that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are p ...
, a solid having trapezoidal faces
* Polite number
In number theory, a polite number is a positive integer that can be written as the sum of two or more consecutive positive integers. A positive integer which is not polite is called impolite... The impolite numbers are exactly the powers of two, an ...
, also known as a trapezoidal number
* Wedge
A wedge is a triangular shaped tool, and is a portable inclined plane, and one of the six simple machines. It can be used to separate two objects or portions of an object, lift up an object, or hold an object in place. It functions by converti ...
, a polyhedron defined by two triangles and three trapezoid faces.
References
Further reading
*D. Fraivert, A. Sigler and M. Stupel''Common properties of trapezoids and convex quadrilaterals''
External links
"Trapezium"
at ''
Encyclopedia of Mathematics
The ''Encyclopedia of Mathematics'' (also ''EOM'' and formerly ''Encyclopaedia of Mathematics'') is a large reference work in mathematics.
Overview
The 2002 version contains more than 8,000 entries covering most areas of mathematics at a graduat ...
''
*
Trapezoid definition
With interactive animations
Trapezoid (North America)
at elsy.at: Animated course (construction, circumference, area)
on ''Numerical Methods for Stem Undergraduate'' * Autar Kaw and E. Eric Kalu,
', (2008) {{Polygons Elementary shapes Types of quadrilaterals