|
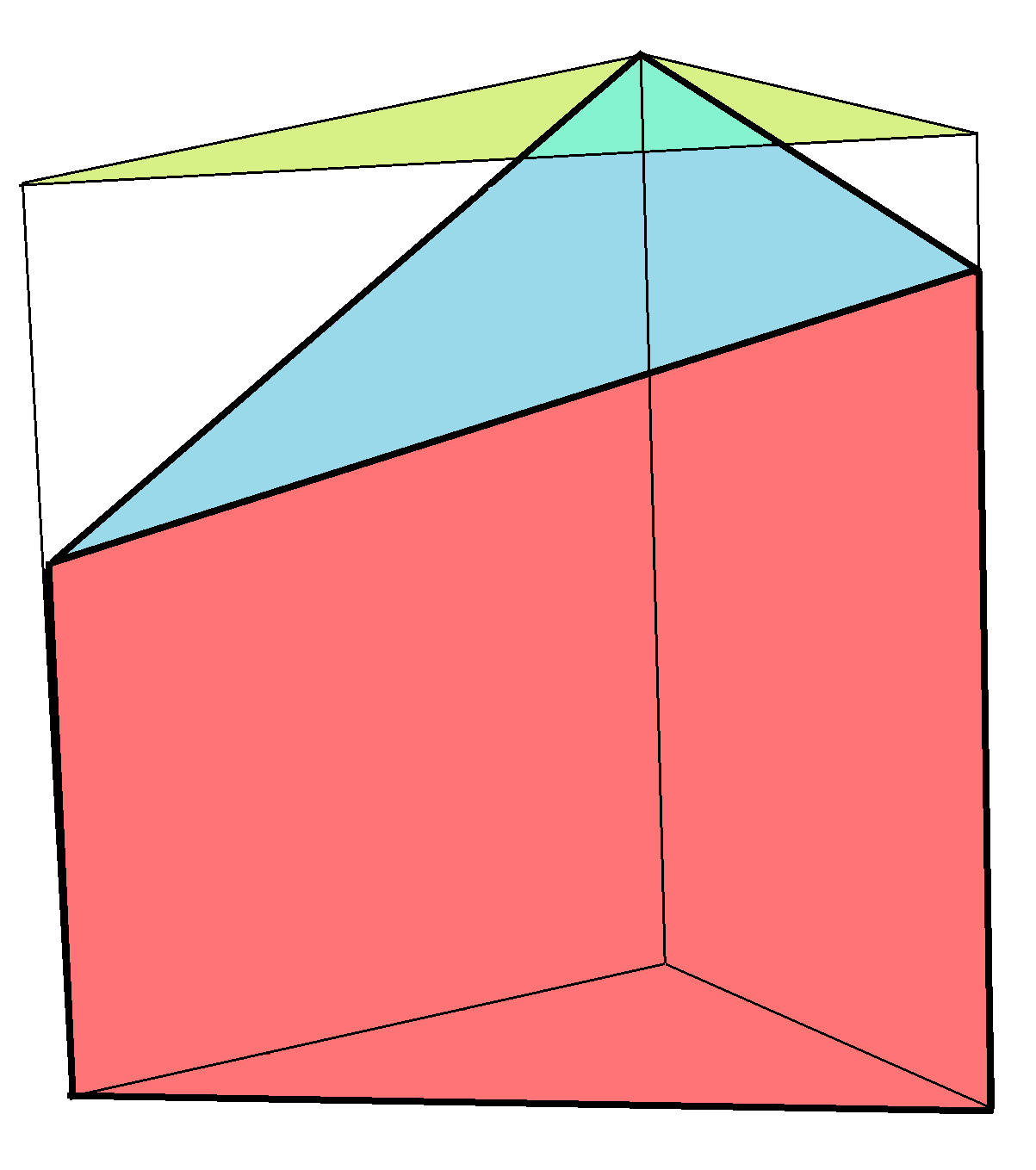
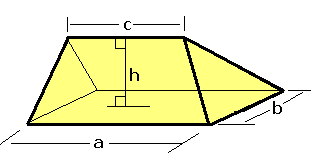
Wedge (geometry)
In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices. A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes. A wedge can also be classified as a digonal cupola. Comparisons: * A wedge is a parallelepiped where a face has collapsed into a line. * A quadrilaterally-based pyramid is a wedge in which one of the edges between two trapezoid faces has collapsed into a point. Volume For a rectangle based wedge, the volume is :V = bh\left(\frac+\frac\right), where the base rectangle is ''a'' by ''b'', ''c'' is the apex edge length parallel to ''a'', and ''h'' the height from the base rectangle to the apex edge. Examples Wedges can be created from decomposition of other polyhedra. For instance, the dodecahedron can be divided into a central cube with 6 wedges covering the cube faces. The orientations of the wedges are such that the triangle and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Wedge
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3- zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spheric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Dodecahedron
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals). It is represented by the Schläfli symbol . Dimensions If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is :r_u = a\frac \left(1 + \sqrt\right) \approx 1.401\,258\,538 \cdot a and the radius of an inscribed sphere (tangent to each of the regular dodecahedron's faces) is :r_i = a\frac \sqrt \approx 1.113\,516\,364 \cdot a while the midradius, which touches the middle of each edge, is :r_m = a\frac \left(3 +\sqrt\right) \approx 1.309\,016\,994 \cdot a These quantities may also be expressed as :r_u = a\, \frac \phi :r_i = a\, \frac :r_m = a\, \frac where ''ϕ'' is the golden ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube In Dodecahedron
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3-zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spherical tiling, and p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has symmetry. If all edge lengths are equal, it is an equilateral square pyramid, the Johnson solid General square pyramid A possibly oblique square pyramid with base length ''l'' and perpendicular height ''h'' has volume: :V=\frac l^2 h. Right square pyramid In a right square pyramid, all the lateral edges have the same length, and the sides other than the base are congruent isosceles triangles. A right square pyramid with base length ''l'' and height ''h'' has surface area and volume: :A=l^2+l\sqrt, :V=\frac l^2 h. The lateral edge length is: :\sqrt; the slant height is: :\sqrt. The dihedral angles are: :*between the base and a side: :::\arctan \left(\right); :*between two sides: :::\arccos \left(\right). Equilateral square pyramid, Johnson solid J1 If all edges have the same length, then the sides are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmentation (geometry)
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that isohedral, each face must be the same polygon, or that the same polygons join around each Vertex (geometry), vertex. An example of a Johnson solid is the square-based Pyramid (geometry), pyramid with equilateral sides (square pyramid, ); it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform polyhedron, uniform (i.e., not Platonic solid, Archimedean solid, prism (geometry), uniform prism, or uniform antiprism) before they refer to it as a “Johnson solid”. As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid () is an example that has a degree-5 vertex. Although there is no obvious restriction tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Obtuse Wedge
{{disambig ...
Obtuse may refer to: * Obtuse angle, an angle of between 90 and 180 degrees * Obtuse triangle, a triangle with an internal angle of between 90 and 180 degrees * Obtuse leaf shape * Obtuse tepal shape * Obtuse barracuda, a ray-finned fish * Obtuse, a neighborhood in Brookfield, Connecticut Brookfield is a town in Fairfield County, Connecticut, United States, situated within the southern foothills of the Berkshire Mountains. The population was 17,528 at the 2020 census. The town is located northeast of New York City, making it part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is ''oblique''. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides. Equivalently, it is a polyhedron of which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelograms. All cross-sections parallel to the base faces are the same triangle. As a semiregular (or uniform) polyhedron A right triangular prism is semiregular or, more generally, a uniform polyhedron if the base faces are equilateral triangles, and the other three faces are squares. It can be seen as a truncated trigonal hosohedron, represented by Schläfli symbol t. Alternately it can be seen as the Cartesian product of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Prism Wedge
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is ''oblique''. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides. Equivalently, it is a polyhedron of which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelograms. All cross-sections parallel to the base faces are the same triangle. As a semiregular (or uniform) polyhedron A right triangular prism is semiregular or, more generally, a uniform polyhedron if the base faces are equilateral triangles, and the other three faces are squares. It can be seen as a truncated trigonal hosohedron, represented by Schläfli symbol t. Alternately it can be seen as the Cartesian product of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.jpg)