|
Tangential Quadrilateral
In Euclidean geometry, a tangential quadrilateral (sometimes just tangent quadrilateral) or circumscribed quadrilateral is a convex polygon, convex quadrilateral whose sides all can be tangent to a single circle within the quadrilateral. This circle is called the Incircle and excircles of a triangle, incircle of the quadrilateral or its inscribed circle, its center is the ''incenter'' and its radius is called the ''inradius''. Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called ''circumscribable quadrilaterals'', ''circumscribing quadrilaterals'', and ''circumscriptible quadrilaterals''. Tangential quadrilaterals are a special case of tangential polygons. Other less frequently used names for this class of quadrilaterals are ''inscriptable quadrilateral'', ''inscriptible quadrilateral'', ''inscribable quadrilateral'', ''circumcyclic quadrilateral'', and ''co-cyclic quadrilateral''.. Due to the risk of confusion with a qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangential Quadrilateral 2
In geometry, the tangent line (or simply tangent) to a plane curve at a given Point (geometry), point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitesimal, infinitely close points on the curve. More precisely, a straight line is tangent to the curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. The point where the tangent line and the curve meet or intersection (geometry), intersect is called the ''point of tangency''. The tangent line is said to be "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a ''tangent line approximation'', the graph of the affine function that best ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degree (angle), degrees, or Pi, /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called square (algebra), squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangency Chords 2
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. The point where the tangent line and the curve meet or intersect is called the ''point of tangency''. The tangent line is said to be "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characterizations In The Four Subtriangles
Characterization or characterisation is the representation of characters (persons, creatures, or other beings) in narrative and dramatic works. The term character development is sometimes used as a synonym. This representation may include direct methods like the attribution of qualities in description or commentary, and indirect (or "dramatic") methods inviting readers to infer qualities from characters' actions, dialogue, or appearance. Such a personage is called a character. Character is a literary element. History The term ''characterization'' was introduced in the 19th century.Harrison (1998, pp. 51-2) Aristotle promoted the primacy of plot over characters, that is, a plot-driven narrative, arguing in his ''Poetics'' that tragedy "is a representation, not of men, but of action and life." This view was reversed in the 19th century, when the primacy of the character, that is, a character-driven narrative, was affirmed first with the realist novel, and increasingly later wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name. When the semiperimeter occurs as part of a formula, it is typically denoted by the letter . Motivation: triangles The semiperimeter is used most often for triangles; the formula for the semiperimeter of a triangle with side lengths :s = \frac. Properties In any triangle, any vertex and the point where the opposite excircle touches the triangle partition the triangle's perimeter into two equal lengths, thus creating two paths each of which has a length equal to the semiperimeter. If are as shown in the figure, then the segments connecting a vertex with the opposite excircle tangency (, shown in red in the diagram) are known as splitters, and :\begin s &= , AB, +, A'B, =, AB, +, AB', =, AC, +, A'C, \\ &= , AC, +, AC', =, BC, +, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pitot Theorem
The Pitot theorem in geometry states that in a tangential quadrilateral the two pairs of opposite sides have the same total length. It is named after French engineer Henri Pitot. Statement and converse A tangential quadrilateral is usually defined as a convex polygon, convex quadrilateral for which all four sides are Tangent lines to circles, tangent to the same inscribed circle. Pitot's theorem states that, for these quadrilaterals, the two sums of lengths of opposite sides are the same. Both sums of lengths equal the semiperimeter of the quadrilateral. The converse implication is also true: whenever a convex quadrilateral has pairs of opposite sides with the same sums of lengths, it has an inscribed circle. Therefore, this is an exact characterization: the tangential quadrilaterals are exactly the quadrilaterals with equal sums of opposite side lengths.. See in particular pp. 65–66. Proof idea One way to prove the Pitot's theorem is to divide the sides of any given tang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Bisector
In geometry, bisection is the division of something into two equal or congruent parts (having the same shape and size). Usually it involves a bisecting line, also called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'', a line that passes through the midpoint of a given segment, and the ''angle bisector'', a line that passes through the apex of an angle (that divides it into two equal angles). In three-dimensional space, bisection is usually done by a bisecting plane, also called the ''bisector''. Perpendicular line segment bisector Definition *The perpendicular bisector of a line segment is a line which meets the segment at its midpoint perpendicularly. *The perpendicular bisector of a line segment AB also has the property that each of its points X is equidistant from segment AB's endpoints: (D)\quad , XA, = , XB, . The proof follows from , MA, =, MB, and Pythagoras' theorem: :, XA, ^2=, XM, ^2+, MA, ^2=, XM, ^2+, MB, ^2=, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangential Trapezoid
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. The point where the tangent line and the curve meet or intersect is called the ''point of tangency''. The tangent line is said to be "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
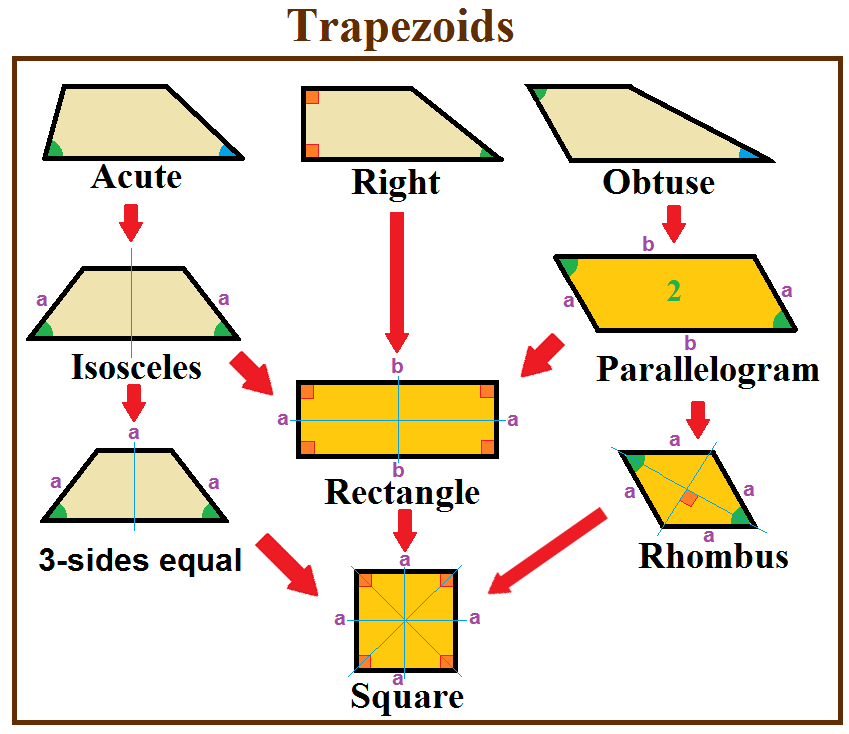
Trapezoid
In geometry, a trapezoid () in North American English, or trapezium () in British English, is a quadrilateral that has at least one pair of parallel sides. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' or ''lateral sides''. (If the trapezoid is a parallelogram, then the choice of bases and legs is arbitrary.) A trapezoid is usually considered to be a convex quadrilateral in Euclidean geometry, but there are also crossed cases. If ''ABCD'' is a convex trapezoid, then ''ABDC'' is a crossed trapezoid. The metric formulas in this article apply in convex trapezoids. Definitions ''Trapezoid'' can be defined exclusively or inclusively. Under an exclusive definition a trapezoid is a quadrilateral having pair of parallel sides, with the other pair of opposite sides non-parallel. Parallelograms including rhombi, rectangles, and squares are then not considered to be trapezoids. Under an inclusive definition, a trapezoid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |