Poncelet–Steiner Theorem

In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions having additional restrictions imposed on the traditional rules. This result, related to the rusty compass equivalence and to Steiner constructions, states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given:

: ''Any Euclidean construction, insofar as the given and required elements are points (or lines), if it can be completed with both the compass and the straightedge together, may be completed with the straightedge alone provided that no fewer than one circle with its center exist in the plane.''

Though a compass can make constructions significantly easier, it is implied that there is no functional purpose of the compass once the first circle has been drawn; the compass becomes redundant. All constructions remain possible, though it is naturally understood that circles and their arcs cannot be drawn without the compass. All points that uniquely define a construction, which can be determined with the use of the compass, are equally determinable without, albeit with greater difficulty.

This means only that the compass may be used for aesthetic purposes, rather than for the purposes of construction. In other words, the compass may be used ''after'' all of the key points are determined, in order to "fill-in" the arcs purely for visual or artistic purposes, if it is desirable, and not as a necessary step toward construction. Nothing essential for the purposes of geometric construction is lost by neglecting the construction of circular arcs.

History

In the tenth century, the Persian mathematician Abu al-Wafa' Buzjani (940−998) considered geometric constructions using a straightedge and a compass with a fixed opening, a so-called ''rusty compass''. Constructions of this type appeared to have some practical significance as they were used by artists Leonardo da Vinci and Albrecht Dürer in Europe in the late fifteenth century. A new viewpoint developed in the mid sixteenth century when the size of the opening was considered fixed but arbitrary and the question of how many of Euclid's constructions could be obtained was paramount.

Renaissance mathematician Lodovico Ferrari, a student of Gerolamo Cardano in a "mathematical challenge" against Niccolò Fontana Tartaglia was able to show that "all of Euclid" (that is, the straightedge and compass constructions in the first six books of Euclid's Elements) could be accomplished with a straightedge and rusty compass. Within ten years additional sets of solutions were obtained by Cardano, Tartaglia and Tartaglia's student Benedetti. During the next century these solutions were generally forgotten until, in 1673, Georg Mohr published (anonymously and in Dutch) ''Euclidis Curiosi'' containing his own solutions. Mohr had only heard about the existence of the earlier results and this led him to work on the problem.

Showing that "all of Euclid" could be performed with straightedge and rusty compass is not the same as proving that ''all'' straightedge and compass constructions could be done with a straightedge and just a rusty compass. Such a proof would require the formalization of what a straightedge and compass could construct. This groundwork was provided by Jean Victor Poncelet in 1822, having been motivated by Mohr's work on the Mohr-Mascheroni theorem. He also conjectured and suggested a possible proof that a straightedge and rusty compass would be equivalent to a straightedge and compass, and moreover, the rusty compass need only be used once. The result of this theorem, that ''a straightedge and single circle with given centre is equivalent to a straightedge and compass'' was proved by Jakob Steiner in 1833.

Major contributions to the field were made by Lazare Carnot, Karl von Staudt, Giuseppe Peano, Joseph Diez Gergonne, and others in the mid-to-late 19th and early 20th centuries, including contributions by Francesco Severi as late as the mid 20th century, even as further research is ongoing.

Controversies

While the theorem itself was not directly implicated, Jean-Victor Poncelet was involved in a plagiarism controversy with Joseph-Diez Gergonne in 1827 over duality principles in projective geometry. This unrelated controversy, the accusation of which was never proven, might occasionally surface in discussions about Poncelet's broader work.

Related constructs

Related constructs that link to this article.

Steiner constructions

The term Steiner construction typically refers to any geometric construction that utilizes the straightedge tool only, and is sometimes simply called a ''straightedge-only construction'', named for Jakob Steiner who studied the subject. As a restricted construction paradigm, no stipulations are made about what geometric objects already exist in the plane or their relative placement; any such conditions are postulated ahead of time. Also, no implications are made about what is or is not possible to construct. Constructions carried out in adherence with the Poncelet-Steiner theorem - relying solely on the use of a straightedge tool without the aid of a compass - are therefore a particular subset of ''Steiner constructions''.

Whereas Steiner constructions study the straightedge tool, the Poncelet-Steiner theorem stipulates the existence of a circle with its center, and affirms that a single circle is equivalent to a compass. Broadly, Steiner constructions may involve any number of circles, including none, already drawn in the plane, with or without their centers. They may also involve all manner of unique shapes and curves preexisting in the plane, provided that the straightedge tool is the only physical tool at the geometer's disposal.

Therefore, all constructions adhering to the Poncelet-Steiner theorem are Steiner constructions, though not all Steiner constructions abide by the strict condition of there being only one circle with its center provided in the plane. The Poncelet-Steiner theorem does not require an actual compass - it is presumed that the circle preexists in the plane - therefore all constructions herein demonstrating the Poncelet-Steiner theorem are Steiner constructions. The single arbitrary circle (with its center), which is postulated in the Poncelet-Steiner theorem, is therefore the minimal amount of information required to allow Steiner constructions to recover the constructive power and versatility of the traditional compass-straightedge paradigm.

Rusty compass

The rusty compass describes a compass whose hinge is so rusted as to be fused such that its legs - the needle and pencil - are unable to adjust width. In essence, it is a compass whose distance is fixed, and which draws circles of a predetermined and constant, but arbitrary radius. Circles may be drawn centered at any arbitrary point, but the radius is unchangeable.

As a restricted construction paradigm, the ''rusty compass constructions'' allow the use of a straightedge and the fixed-width compass. The rusty compass equivalence:

:''All points necessary to uniquely describe any compass-straightedge construction may be achieved with a straightedge and fixed-width compass.''

It is naturally understood that the arbitrary-radius compass may be used for aesthetic purposes; only the arc of one specific predetermined fixed-width compass may be used for construction.

As the rusty compass relates to the theorem

In some sense, the rusty compass is a generalization and simplification of the Poncelet-Steiner theorem. Though not more powerful, it is certainly more convenient. The Poncelet-Steiner theorem requires a single circle with arbitrary radius and center point to be placed in the plane. As it is the only drawn circle, whether or not it was drawn by a rusty compass is immaterial and equivalent. The benefit of general rusty compass constructions, however, is that the compass may be used repeatedly to redraw circles centered at any desired point, albeit with the same radius, thus simplifying many constructions. Naturally if all constructions are possible with a single circle arbitrarily placed in the plane, then the same can surely be said about a straightedge and rusty compass, with which at least one circle may be arbitrarily placed.

It is known that a straightedge and a rusty compass is sufficient to construct all that is possible with straightedge and standard compass - with the implied understanding that circular arcs of arbitrary radii cannot be drawn, and only need be drawn for aesthetic purposes rather than constructive ones. Historically this was proven when the Poncelet-Steiner theorem was proven, which is a stronger result. The rusty compass, therefore, is no weaker than the Poncelet-Steiner theorem. It should also be intuitively clear that a rusty compass cannot be any stronger than a standard compass. As the rusty compass is at least as strong as the circle and no stronger than the standard compass, and the latter two are proven equivalent by the Poncelet-Steiner theorem, so too must the rusty compass be equivalent.

The Poncelet-Steiner theorem reduces Ferrari's rusty compass equivalence, a claim at the time, to a single-use compass:
:''All points necessary to uniquely describe any compass-straightedge construction may be achieved with only a straightedge, once the first circle has been placed.''
The Poncelet-Steiner theorem takes the rusty compass scenario, and breaks the compass completely after its first use.

There is a subtle distinction, however, which makes the single use rusty compass slightly more useful. With a single-use compass, the geometer may place the first circle arbitrarily, as it suits convenience, even after other constructions have begun. The Poncelet-Steiner theorem, on the other hand, presumes the geometer has no control over the placement of the circle or over the constructions undertaken, making the two independent.

Associated concepts and vocabulary

Various other notions, tools, terminology, etc., is often associated (sometimes loosely) to the Poncelet-Steiner theorem. Some are listed here.

Projective geometry, as it relates to the Poncelet-Steiner Theorem

Projective geometry is the study of the geometric properties that are invariant under projective transformations. Though a distinct topic in its own right, many of the concepts of projective geometry are applied here to Steiner constructions. Jean-Victor Poncelet was a major contributor to the subject when he postulated the theorem of this article, which Jakob Steiner later proved. Many of the related concepts developed in projective geometry include but are not limited to: concurrence, "points at infinity", perspective and perspectivity, projectivity, ratios and cross-ratios, conjugates, stable or fixed points of involutions, invariants, duality, homogeneity and homography, linear transformations, projective harmonics, pencils (of lines or of circles), and others. A thorough treatment of Steiner constructions and their proofs require a background in projective geometry, though the subject of projective geometry is not restricted to straightedge-only constructions.

Points at Infinity

Points at infinity are a rather abstract notion found in projective geometry. Also called ''ideal points'', they refer to the "endpoint" of a line: the point where the line intersects the horizon of the plane. Rather than a coordinate, they are identified by a direction; any line therefore identifies a point at infinity. All parallel lines share in the same ideal point, and thus any two parallel lines are said to intersect at the same point at infinity, akin to Euclid's conception of parallels intersecting. In fact each direction along the line toward the infinite identify the same ideal point; each line is associated with one such point at infinity, not two. As each line orientation in the plane identifies a distinct point at infinity, the collection of these are called the ''line at infinity'', which may also in some contexts be viewed as a circle of infinite radius with no definable center. In some sense these points "complete" the plane; the notion is vital to transforming the traditional Euclidean plane (an affine space) into a projective space. It is through the notion of points at infinity that many Steiner constructions become possible, provable, and fully generalized.

Pencils of lines or of circles

The term pencil refers to a set of geometric objects that all share in a common property which is uniquely identifiable by precisely two of its elements, and is a term usually only employed in geometric contexts. The property in question is usually expressed as a geometric object also. For example, in the case of a ''pencil of lines'', which is a set containing only lines, the property is typically that of passing through the same point, also called concurrence. Two lines will intersect at a point - even if the point is "at infinity" in the case of parallel lines - where the point of concurrence (i.e. intersection) is the geometric object defining the property; any other line that also intersects at the same point is therefore in the pencil, and conversely those lines that do not are not in the pencil.

In the case of a ''pencil of circles'', a common coaxial system - that is, having the same radical axis (which is a line) - is the usual interpretation. Any other circle is included in the pencil if it shares the same radical axis with any other pair of circles already in the pencil. Indeed, a ''pencil of points'' typically refers to the set of all points on a given line, as any and every two points from this set will define the same line.

Though these are the usual meanings, any property the geometer chooses is valid, provided that it takes two elements - no more or less - to establish the underlying set. In essence, a pencil is an entire set of (potentially infinite) geometric objects which are wholly defined by any two, and every two, distinct members from its set. Any two like-objects therefore define the entire set to which other like-objects do or do not belong.

Historical publications

Pencils are a common theme in many geometry publications throughout history, though the term is less commonly used today. This article does not explicitly refer to pencils, though some of the constructions found herein, and in projective geometry more broadly, do in fact implicitly use the notion of a pencil, often by different terminology or by explicitly referring to the underlying property. The term is herein defined for the readers convenience due to its common usage within many of the cited references that are used to support the content of this article, wherein the term is rarely defined.

Generalizations of the pencil

Pencils have been generalized to higher dimensions as well (e.g. a ''pencil of planes''). For contrast, the term ''flat pencil'' refers to pencils in a two-dimensional space, and ''spatial pencil'' for three-dimensions.

The notion of pencils can also be generalized such that more than two elements establish the set. A set of geometric objects defined by precisely three of its elements, no more or less, is called a ''bundle''. One example of a ''bundle of points'' is the set of points on the arc of a circle. Similarly, though there is no specialized term for it, five points in the plane define a conic section, any five points on which may be used to establish the same curve.

Steiner's theorem / Hilbert's error

: ''Not to be confused for '' Steiner's parallel axis theorem'', ''Steiner's porism'', or the ''Steiner–Lehmus theorem''.

If only one circle is to be given and no other special information, Steiner's theorem implies that the center of the circle must be provided along with the arc of the circle. This is done by proving the impossibility of constructing the circle's center from straightedge alone using only a single circle in the plane, without its center. An argument using projective transformations and Steiner's conic sections is used.

: '' With only one circle provided in the plane, its center cannot be constructed by straightedge alone.''

Also attributed to David Hilbert and known as ''Hilbert's Error'', a naïve summary of the proof is as follows. With the use of a straightedge tool, only linear projective transformations are possible, and linear projective transformations are reversible operations. Lines project onto lines under any linear projective transformation, while conic sections project onto conic sections under a linear projective transformation, but the latter are skewed such that eccentricities, foci, and centers of circles are not preserved. Under different sequences of mappings, the center does not map uniquely and reversibly. This would not be the case if lines could be used to determine a circle's center. As linear transformations are reversible operations and would thus produce unique results, the fact that unique results are not possible implies the impossibility of center-point constructions. The uniqueness of the constructed center would depend on additional information - not provided by a single circle - which would make the construction reversible.

Thus, it is not possible to construct everything that can be constructed by straightedge and compass using only the straightedge alone. Consequently, requirements on the Poncelet-Steiner theorem cannot be weakened with respect to the circle center. If the centre of the only given circle is not provided, it cannot be obtained by a straightedge alone. Many constructions are impossible with straightedge alone. Something more is necessary, and a circle with its center identified is sufficient.

Alternative Frameworks to the Single Circle with Center

Alternatively, the center may be omitted with sufficient additional information. This is not a weakening of the Poncelet-Steiner theorem, merely an alternative framework. Nor is it a contradiction of Steiner's Theorem which hypothesizes only a single circle. The inclusion of this sufficient alternative information, which in most cases includes at least two circles, disambiguates the mappings under the projective transformations, thus allowing various Steiner constructions to recover the circle center.

Most of these alternatives requires at least two circles devoid of their centers, plus some other unique piece of information. Some alternatives include two concentric or two intersecting circles, or three circles, or other variations wherein the provided circles are devoid of their centers. In each, some additional unique-but-sufficient criterion is met, such as concentricity, intersection points, a third circle, etc., respectively. Other configurations exist (see a later section for a more detailed list), such as some one-circle configurations, where sufficient alternative information is provided. In any of these cases, the center of a circle can be constructed, thereby reducing the problem to the Poncelet-Steiner theorem hypothesis (with the added convenience of having additional circles in the plane, all of whose centers may now be constructed).

Constructive proof outline

To prove the theorem, each of the basic constructions of compass and straightedge need to be proven to be possible by using a straightedge alone (provided that a circle and its center exist in the plane), as these are the foundations of, or elementary steps for, all other constructions. That is to say, all constructions can be written as a series of steps involving these five basic constructions:

#Creating the line through two existing points.
#Creating the circle through one point with centre another point.
#Creating the point which is the intersection of two existing, non-parallel lines.
#Creating the one or two points in the intersection of a line and a circle (if they intersect).
#Creating the one or two points in the intersection of two circles (if they intersect).

If these fundamentals can be achieved with only a straightedge and an arbitrary circle (with center) embedded in the plane, the claim that is the theorem of this article will have been proved.

#1 – A line through two points

This can be done with a straightedge alone. Neither a compass nor a circle is required.

#2 – A circle through one point with defined center

It is understood that the arc of a circle cannot be drawn without a compass. A circle is considered to be given by any two points, one defining the center and one existing on the circumference at radius. Any such pair define a unique circle, although the converse is not true: for any given circle there is no unique pair defining it. In keeping with the intent of the theorem which we aim to prove, the actual circle need not be drawn but for aesthetic reasons. It is the claim of this theorem that a circle defined in this way is sufficient and fully useful for construction; even without its arc drawn the circle ''exists'' implicitly and may still be utilized. Thus, we may take construction #2 as proved if the other four are achievable. That is, if all constructions which involve a circle may be achieved with a circle defined according to its center and circumference point, we may say there is no distinction between the circle defined in such a way and the drawn arc. This claim will be revisited later in the article.

#3 – Intersection of two lines

This construction can also be done directly with a straightedge.

#4, #5 – Intersections involving the circle

Thus, to prove the theorem, only constructions #4 and #5 need be proven possible using only a straightedge and a given circle with its center.

Notes and Caveats for the Constructive Proof

Some notes and commentary regarding the theorem, the proofs, and related topics of consideration follow.

Regarding the Circle

Circle nomenclature

In the constructions below, a circle defined by a center point and a point on its circumference, , through which the arc of the circle passes (or would pass if compass-drawn), is denoted . As most circles are not compass-drawn, center and circumference points are named explicitly. The arc, if drawn, may also be named, such as ''circle'' or ''arc'' . Per the theorem, when a compass-drawn circle is provided it is simply referred to as the ''given circle'' or the ''provided circle''. Every compass-drawn circle is interchangeable for the purposes of this theorem.

Circle generality

The provided circle should always be assumed to be placed arbitrarily in the plane with an arbitrary radius. Many examples of constructability with a straightedge one may find in various references on and offline, will presume that the circle is not placed in general position. Instead, for example, the constructability of a polygon may postulate that the circle is circumscribing. Such assumptions simplify a construction but does not prove generality of the claim of constructability. For the purposes of this theorem, we may assume that the circle is indeed fully general: the center point and radius are completely arbitrary and purely independent of all other points in the plane. This is what makes the single-use rusty compass more convenient for the geometer; we avoid this scenario.

Usage of the arc of the provided circle(s)

The intersection points between any line and the given circle (or given arc of a circle) may be found directly, as can the intersection points between the arcs of two circles, if provided. The Poncelet-Steiner Theorem does not prohibit the normal treatment of circles already drawn in the plane; normal construction rules apply. The theorem only prohibits the construction of new circular arcs with a compass.

Regarding Application

Usability

The constructive proof does not merely serve as a proof of the theorem, but also demonstrates the practical application of the most basic constructions, such that the claim of constructability with a straightedge could be employed in practice, in the most general case. Since all geometric constructions can be expressed as a sequence of the five basic constructive steps, and the below constructions demonstrate and justify each of these, necessarily, in order to prove the theorem, therefore all possible constructions may be implemented accordingly.

Generality and simplicity

Some specific construction goals - such as for example the construction of a square - may potentially have relatively simple construction solutions, which will not be demonstrated here in the article, despite its simplicity. The omission of such constructions mitigate the length of the article. The purpose of these decisions is that such constructions may not be ubiquitous or sufficiently useful, particularly for the purposes of proving the theorem. Though the theorem and the constructions found herein can be used to construct any figure, no claims are made about the existence of simpler (straightedge-only) alternatives for any specific construction, or given any specific set of initial starting conditions.

Arbitrary point placement

Steiner constructions and those constructions herein proving the Poncelet-Steiner theorem require the arbitrary placement of points in space. These constructions rely on the concept of fixed points (and fixed lines), wherein the resultant construction is independent of the arbitrariness employed during construction. These are known as transformation invariants. In some construction paradigms - such as in the geometric definition of the constructible number - arbitrary point placement may be prohibited. Traditional geometry has no such restriction on point placement. With such a restriction against the placement of arbitrary points, the single circle is indeed weaker than the compass. This can be reconciled, however. Steiner constructions may be used as a basis for the set of constructible numbers if one only enters into the set those points which are fixed/invariant, disregarding the arbitrarily placed points, and the unfixed/variant points they derive, that are required during a construction.

Regarding the Proof and Approach

Doubts about constructions #1 or #3: defining lines and intersecting them

Any doubts about constructions #1 or #3 would apply equally to the traditional construction paradigms which do involve the compass, and thus are not concerns unique to the Poncelet-Steiner theorem or to Steiner constructions more generally. These concerns are in fact intrinsic to the straightedge itself, and have broad ramifications for traditional geometry beyond the scope of straightedge-only constructions. Their justifications - if any need be given - will not be explored in this specialized article, but would be more suited to the geometry article.

Doubts about construction #2: defining and constructing circles

Construction #2 should not be of concern. Even though it is undisputed that a unique circle is defined by a center point and a point on its circumference, the pertinent question is whether or not this is sufficient information for the purposes of straightedge-only construction, or if the drawn arc is required. As per the fundamental constructions, the arc of the circle is only ever used in traditional construction paradigms for the purposes of circle-circle and circle-line intersections, therein the arc of the circle is used directly to identify intersection points. Thus if constructions #4 and #5 are satisfiable without the arc of the circle with which to intersect, then it will prove the non-necessity of drawing the arc. This would therefore imply that construction #2 is effectively satisfied by a simple labeling of two points, identifying the unique circle. This claim will be revisited later in this article.

Choice of construction among variants

In general constructions there are often several variations that will produce the same result. The choices made in such a variant can be made without loss of generality. However, when a construction is being used to prove that something can be done, it is not necessary to describe all these various choices and, for the sake of clarity of exposition, only one variant will be given below. This serves as both proof of possibility and demonstration of methodology. The variants chosen below are done so for their ubiquity and generalizability in application rather than their simplicity or convenience under any particular set of special conditions.

Proofs of sub-constructions

For simplicity of exposition, each of the constructions below are not themselves fully proven. Their proofs may be found in other articles and papers. This article aims to prove the claim that is the theorem of this article by demonstration of the fundamental constructions of which the compass is capable. It does so by relying on a number of sub-constructions, which are provided without rigorous proofs of their own, though such proofs do exist. Though the constructions are fully provided and demonstrated, proof that they do what they claim to do is left to the reader to research. This article does not prove the theorem from axiom, postulate, or first principles; it presumes that certain other sub-constructions are accepted to be true as-is.

Alternative proofs

Alternative proofs do exist for the Poncelet-Steiner theorem, originating in an algebraic approach to geometry. Relying on equations and numerical values in real coordinate space, $\mathbb^2$, via an isomorphism to the Euclidean plane, this is a fairly modern interpretation which requires the notions of length, distance, and coordinate positions to be imported into the plane. The algebraic proof illustrates the dependence of the theorem on Archimedes' axiom, which cannot be formulated in first-order logic. This is well beyond the scope of traditional geometry. This article takes a more traditional approach and proves the theorem using pure geometric constructive techniques, which also showcases the practical application.

Constructive proof

The proof of the theorem and useful straightedge-only constructions follow.

Some preliminary constructions

To prove the above constructions #4 and #5, which are included below, a few necessary intermediary constructions are also explained below since they are used and referenced frequently. These are also straightedge-only constructions. All constructions below rely on basic constructions #1,#2,#3, and any other construction that is listed prior to it.

Parallel of a line having a colinear bisected segment

This construction does not require the use of the given circle. Naturally any line that passes through the center of the given circle implicitly has a bisected segment: the diameter is bisected by the center. The animated GIF file embedded at the introduction to this article demonstrates this construction - relying on the bisected diameter; the arc of the circle is never used - which is reiterated here without the circle and with enumerated steps.

Given an arbitrary line (in black) on which there exist two points and , having a midpoint between them, and an arbitrary point in the plane (assumed not to be on line ) through which a parallel of line is to be made:
# Construct a line (in red).
# Construct a line (in orange).
# Define an arbitrary point on line .
# Construct a line (in green).
# Construct a line (in light blue).
# Lines and intersect at point .
# Construct a line (in magenta).
# Lines and intersect at point .
# Construct a line (in dark blue), the desired parallel.

In some literature the bisected line segment is sometimes viewed as a one-dimensional "circle" existing on the line. Alternatively, some literature views the bisected line segment as a two dimensional circle in three dimensional space with the line passing through a diameter, but not parallel to the plane, thus intersecting the plane of construction at two points on the circumference with the midpoint simply being the prescribed circle center.

This construction is a special case of the projective harmonic conjugate construction, which is not demonstrated in this article.

Creating a bisected segment on a line

If the line passes through the center of a circle, the segment defined by the diameter through the circle is bisected by the center of the circle. In the general case, however, any other line in the plane may have a bisected segment constructed onto it. This construction does require the use of the given circle.

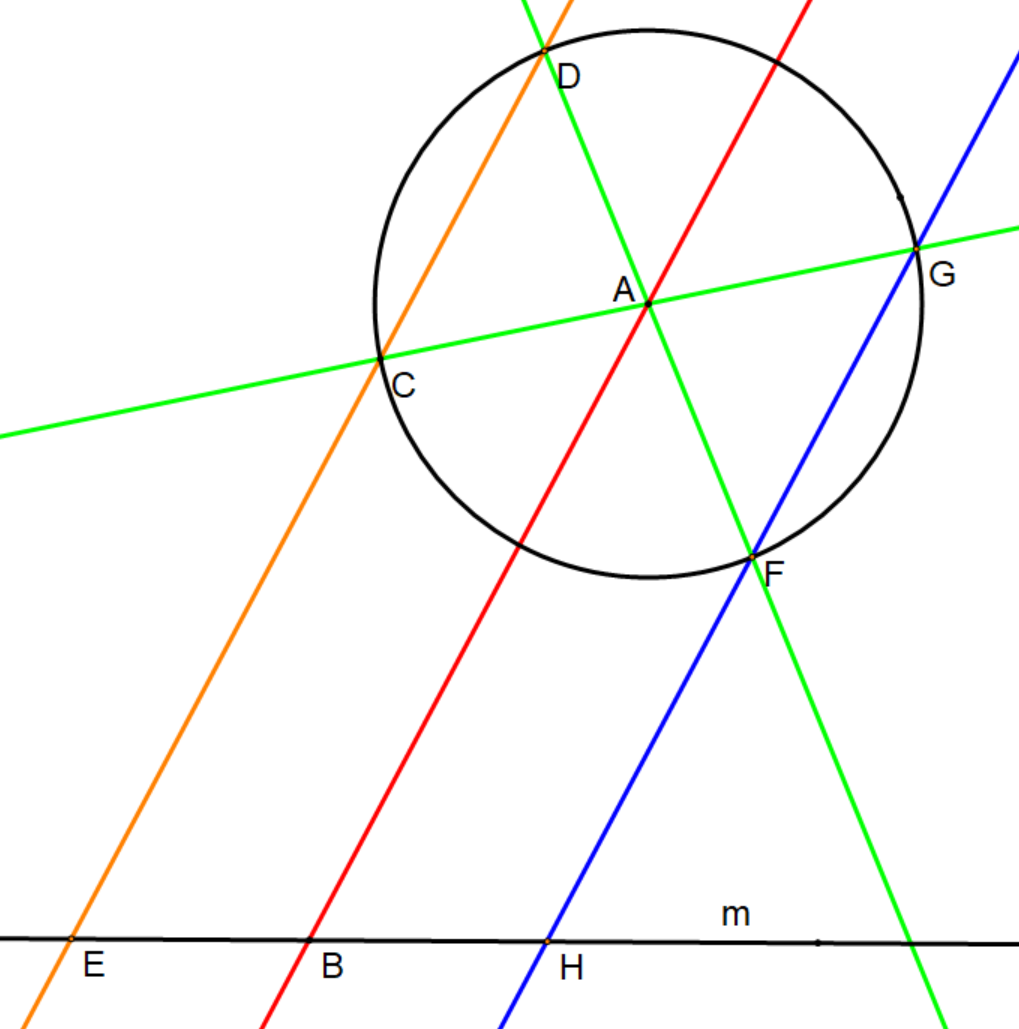
Given a line, (in black), and a circle centered at , we wish to create points , , and on the line such that is the midpoint:
# Draw an arbitrary line (in red) passing through the given circle's center, , and the desired midpoint (chosen arbitrarily) on the line .
#* Notice that the red line, , passes through the center of the circle and highlights a diameter, bisected by the circle center. Any parallel may be made from this line according to the previous construction.
# Choose an arbitrary point on the given circle
#* For convenience the point should be chosen such that line and line are not perpendicular.
# Construct a line (in orange), passing through , that is parallel to the red line .
#* If point is on the perpendicular of through the circle center, the parallel would be a tangent to the circle. The construction is possible by other means not listed in this article, but it is also unnecessary to choose such a point.
#* This parallel intersects the given circle at .
#* This parallel also intersects the black line at , defining one end of the line segment.
# Create two lines (in green), and , that each pass through the given circle's center.
#* These green lines intersect the given circle at points and , respectively.
# Line (in blue) intersects the line at , defining the other endpoint of the line segment.
#* Segment now exists coincident with line and having midpoint .

As point is chosen arbitrarily, there is no need for it to inconveniently be on the perpendicular of line through the circle center. If however it is, line is merely the tangent line to the circle through point , which is coincident to point . This construction is possible though the construction is not listed in this article. Points and may be constructed as before, and will also equal one another. And again, line is merely the tangent line to the circle at that point. Thus points , and their midpoint may be found, as before, with only a minor change adding a subconstruction.

Constructing a parallel of any line

This construction does require the use of the given circle. In order to generalize the parallel line construction to all possible lines, not just the ones with a collinear bisected line segment, it becomes necessary to have additional information. In keeping with the Poncelet-Steiner theorem, a circle (with center) is the object of choice for this construction.

To construct a parallel line of any given line, through any point in the plane, we trivially combine two constructions:
# Any line from which a parallel is to be made must have a bisected segment constructed onto it, if one does not already exist.
# A parallel is then constructed according to the previous parallel construction involving the collinear bisected segment.

In alternative constructions, which are not demonstrated in this article, a parallel may be constructed from any pair of lines which are already parallel to one another; thus a third parallel may be produced from any two, without the use of a circle. Additionally, a parallel of any line may be constructed whenever there exists in the plane any parallelogram, also without the use of a given circle.

Constructing a perpendicular line

This construction does require the use of the given circle and takes advantage of Thales's theorem.

From a given line , and a given point in the plane, a perpendicular to the line is to be constructed through the point. Provided is the given circle .
# If the desired line from which a perpendicular is to be made, , does not pass through the given circle - as is depicted - or it also passes through the given circle's center, then a new parallel line (in red) may be constructed arbitrarily such that it does pass through the given circle but not its center, and the perpendicular is to be made from this line instead.
# This red line which passes through the given circle but not its center, will intersect the given circle in two points, and .
# Draw a line (in orange), through the circle center.
#* This line intersects the given circle at point .
#* Angle is 180°.
# Draw a line (in light green).
#* This line is perpendicular to the red (and therefore the black) lines, and .
#* By Thales's Theorem, angle is 90°.
# Construct a parallel of line through point using previous constructions.
#* A perpendicular of the original black line, , now exists in the plane, line .
#* A parallel of any line may be constructed through any point in the plane.

If the line from which a perpendicular is to be made does pass through the circle center, an alternative approach would be to construct the tangent lines to the circle at the lines points of intersection, using Steiner constructions. This is not demonstrated in this article.

Another option in the event the line passes through the circle's center would be to construct a parallel to it through the circle at an arbitrary point. An isosceles trapezoid (or potentially an isosceles triangle) is formed by the intersection points to the circle of both lines. The two non-parallel sides of which may be extended to an intersection point between them, and a line drawn from there through the circle's center. This line is perpendicular, and the diameter is bisected by the center.

By an alternative construction not demonstrated in this article, a perpendicular of any line may be constructed without a circle, provided there exists in the plane any square.

Constructing the midpoint of any segment (segment bisection)

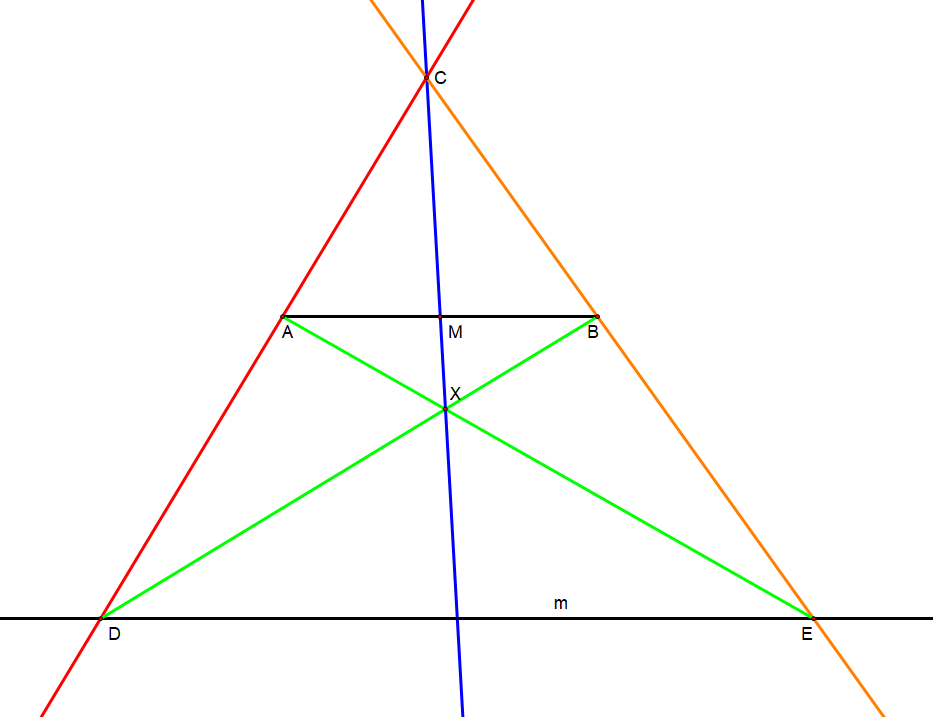
Given is a line segment , which is to be bisected. Optionally, a parallel line exists in the plane.

# If the line , which is parallel to line segment , does not exist in the plane then it must be constructed according to earlier constructions using the given circle in the plane (not depicted).
#* A given circle in the plane is not required for this construction if the parallel already exists.
#* The parallel may be placed in the plane arbitrarily, so long as it is not collinear with the line segment.
# Arbitrarily choose a point in the plane which is not collinear with the line or the line segment.
#* One may, alternatively, construct point as the intersection of lines and , provided that points and already exist on a parallel line .
# Draw a line (in red), intersecting line at point .
# Draw a line (in orange), intersecting line at point .
# Draw two lines, and (each in light green), intersecting each other at point
# Draw a line (in blue), intersecting segment at point .
#* Point is the desired midpoint of segment .
#* Line also bisects segment

For added perspective, in some sense this construction is a variant of a previous construction of a parallel from a bisected line segment, and is therefore also a special case of the projective harmonic conjugate (not provided in this article). It is the same set of lines when taken on whole, but constructed in a different order, and from a different initial set of conditions, arriving at a different end goal.

Since any arbitrary segment on one of two parallel lines can be bisected, and any line with a bisected segment on it may have a parallel constructed, the two scenarios are geometrically equivalent propositions. They imply one another; a simple construction can convert one scenario into the other using no additional information.

It may also be worth noting that if trapezoid is an isosceles trapezoid then the bisector is also a perpendicular bisector. An isosceles trapezoid is formed when lines and each pass through a circle and intersecting at those defining points, and in which case the perpendicular bisector is a centerline to the circle. If line is itself a centerline then a circle center has been found, if it was not already known.

Additionally, if is a parallelogram then the construction will fail as it is written. Point may be found normally, but point will not exist. Instead the bisecting line can be constructed as a parallel of lines or through point . However, in an alternate construction, any line segment may be bisected whenever a parallelogram exists in the plane (not demonstrated in this article).

Rotating a line segment

Line segment rotation is a useful construction but may rarely be used in practice. It is necessary to demonstrate in order to fully generalize the theorem.

To define a circle only the center and one point - any point - on the circumference is required. In principle a new point is constructed such that circle is equal to circle , though the point is not equal to point . In essence, segment is rotated about the axis point , to , for a different set of defining points for the same circle.

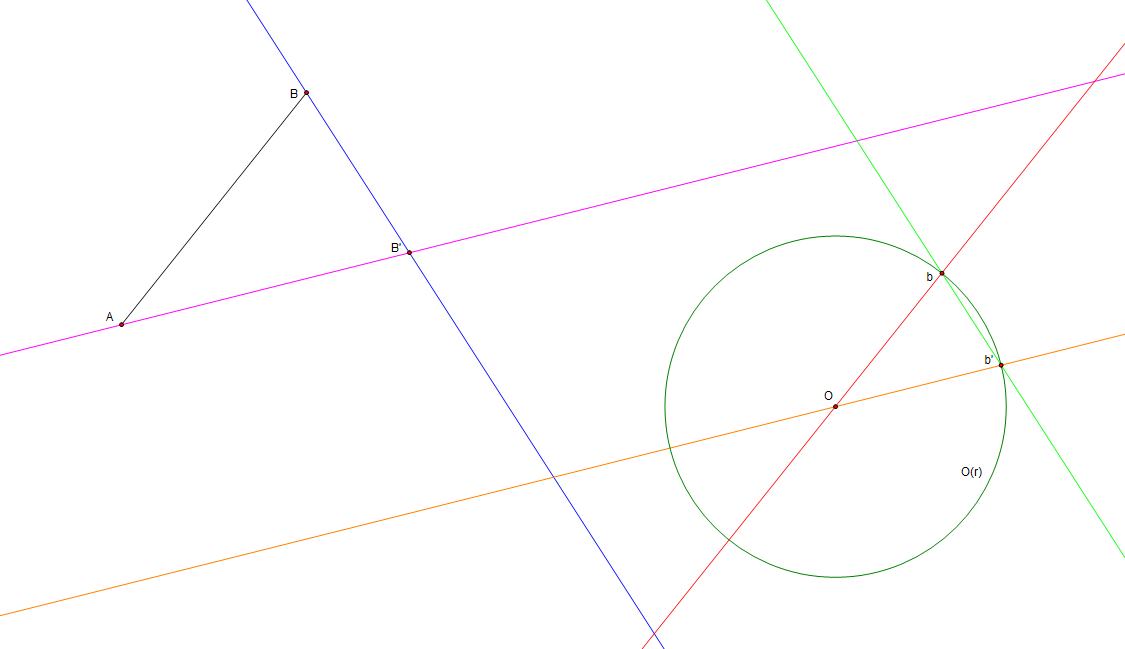
One way of going about this which satisfies most conditions is as follows:
# Draw the line segment (in black).
# Construct a parallel (in red) of line through the center, point , of the given circle.
#* The parallel intersects the given circle at some point .
# Choose a point arbitrarily on the given circle not colinear with line .
# Draw a line (in orange).
# Construct a parallel line to through point (in magenta).
# Draw a line (in light green), connecting the points on the circles circumference.
# Construct a parallel of line through point (in blue).
# Intersect the blue and pink parallels, from points and , respectively.
#* This is point .
#* Point is the desired point, rotating the line segment and defining the same circle centered at .

This construction will fail if the desired rotation is diametrically opposite the circle (i.e. a half-circle rotation). One solution to this scenario is to employ two separate rotation constructions, neither one a half-circle rotation from the previous, one acting as an intermediary step. Choose any rotation angle arbitrarily, complete the rotation, then choose the supplementary angle and perform the rotation a second time.

There does exist a second, alternative rotation construction solution, based on projections and perspective points. Though it avoids the aforementioned half-circle rotation complication, it does have its own complications, which are similarly resolved with intermediary rotation constructions. The construction is no more versatile. It is not demonstrated in this article.

Constructing the radical axis between circles

This construction does require the use of the given circle (which is not depicted) for the sub-constructions referenced in the steps below, which were previously demonstrated.

Suppose two circles and are implicitly given, defined only by the points , , , and in the plane, with their centers defined, but are not compass-constructed. The radical axis, line (in dark blue), between the two circles may be constructed:
# Draw a line (in orange) through the circle centers.
# Draw a line segment (in red) between the points on the circumference of the circles.
# Find the midpoint, , of segment .
# Draw lines and (both in light green), connecting the segment midpoint with each of the circle centers.
# Construct a line (in purple) passing through point , and perpendicular to .
#* Line is the radical axis between circle and circle , as it passes through the point of intersection and is perpendicular to the line through centers, .
# Construct a line (in dark green) passing through point , and perpendicular to .
#* Line is the radical axis between circle ''='' and circle .
# Lines and intersect at point .
#* Point is the power center between circles , , and , and therefore is the unique point that lies on the radical axis between any two of the three circles.
#* By transitivity, therefore, point exists on the radical axis between circles and .
#* If the lines and are parallel then the segment midpoint is on the line - the centers of circles , , and are colinear - and the construction will fail. An alternative approach is required (see below).
# Construct a line (in dark blue) perpendicular to line and passing through point .
#* Line is the desired radical axis.

In the event that the construction of the radical axis fails due to there not being an intersection point between parallel lines and , which results from the coincidental placement of the midpoint on the line , an alternative approach is required. One such approach is to rotate the segment about the axis point (the center of circle ). Once arrived at the arbitrary rotation , which defines the same circle, the radical axis construction can begin anew without issue.

Intersecting a line with a circle (Construction #4)

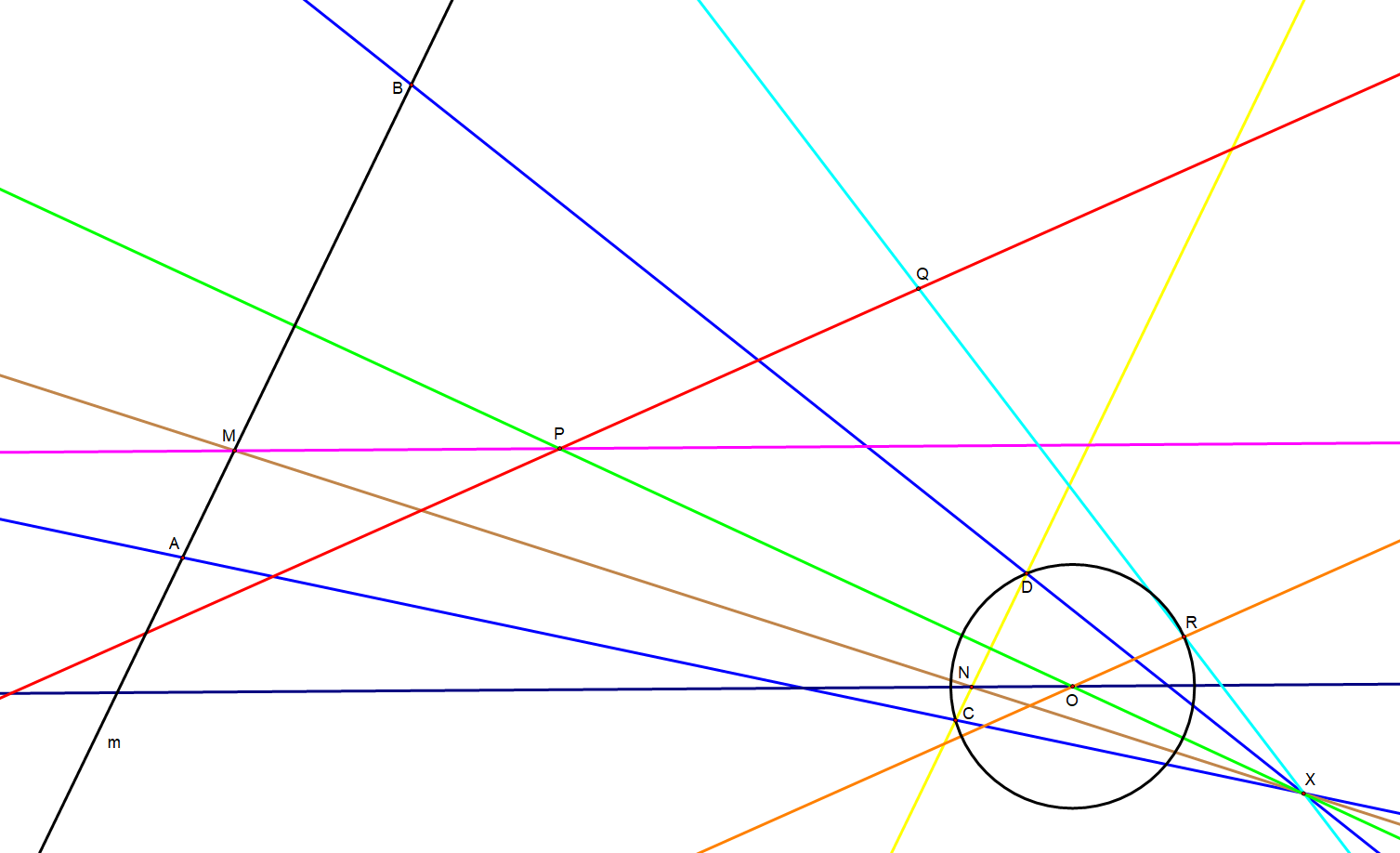
This construction does require the use of the provided circle, . Any line may be naturally intersected with any compass-drawn circle.

Given is the line (in black) and the circle , which is not compass-constructed. The intersection points of the circle and the line , which are point and , may be constructed:
# Draw a line (in red) through the points defining the circle.
#* If point is colinear with line then segment will need to be rotated about the center point of the circle, and this construction restarted anew.
# Construct a parallel (in orange) of line through the center of the provided circle.
#* The parallel intersects the provided circle at two points, one of which is arbitrarily chosen: .
# Draw a line (in light green), through the centers of the two circles (i.e. the one provided by compass construction and the one which is to be intersected).
# Draw a line (in light blue), connecting the two points on the circumferences of the two circles.
# Intersect the lines and at point .
#* If point does not exist due to lines and being parallel - which results from circles and having equal radii - then refer back to step 2 and choose the alternate point of intersection, .
# Choosing a point arbitrarily on line , such that it is not on line , draw a line (in magenta).
#* For construction simplicity and only if line is not parallel to line , lines and may be coincident.
# Draw a line (in brown).
# Construct a parallel (in dark purple) of line through the center of the provided circle.
#* The parallel intersects the line at a point .
# Construct a parallel (in yellow) of line through the point .
#* The parallel intersects the provided circle at points and .
#* If the parallel does not intersect the provided circle then neither does the line intersect circle .
# Draw lines and (both in dark blue).
#* These lines both intersect line at points and , respectively.
# Points and are the desired points of intersection between the line and the circle .

Intersecting two circles (Construction #5)

The intersection between two circles becomes a trivial combination of two earlier constructions.

Suppose two circles and are implicitly given, defined only by the points , , , and in the plane, with their centers defined, but are not compass-constructed. Their intersection points, and , may be constructed:

# Construct the radical axis, line , between the two circles.
# Construct the intersection points, and , between the radical axis, line , and either one of the two circles arbitrarily chosen.
#* The radical axis is a line, so this construction is possible per the previous circle-line intersection construction (basic construction #4).
# These points are the desired points of intersection of the circles.
#* The two circles and the radical axis all intersect at the same loci of points: two distinct points, one point if tangential, or none if they do not intersect.
#* If the radical axis does not intersect one circle then it intersects neither, and neither do the two circles intersect.

A circle through one point centered at another point (Construction #2, revisited)

The second basic construction - describing a full circle with just its center and one point at radius defining circumference - never needed an arc to be constructed with the compass in order for the circle to be utilized in constructions. Namely, the intersections of circles both with circles and with lines, which together are the essence of all constructions involving a circle, are achievable without the arc. That is, any circle defined by a center point and a point on its circumference may be intersected by any line and by any other similarly-defined circle; nothing is lost by omitting the arc. Rather than directly intersecting lines and circles with an arc of a circle, as would have been done in traditional geometry, intersections have been shown to be constructible using the straightedge in an indirect manner. Thus defining a circle by its center and by any arbitrary point on its circumference is sufficient to fully describe the entire circle and utilize it in constructions. As such, the arc only serves an aesthetic purpose. Basic construction #2 is satisfied.

Conclusion

Since all five basic constructions have been shown to be achievable with only a straightedge, provided that a single circle with its center is placed in the plane, this proves the Poncelet-Steiner theorem. Any compass-straightedge construction may be achieved with the straightedge alone by describing their constructive steps in terms of the five basic constructions, and then utilizing the constructions in the above proof, if a circle with its center point is provided anywhere in the plane.

Practical Application

The Poncelet-Steiner theorem is a fundamental result in projective geometry that has significant practical applications for geometers and mathematicians. It serves greater purpose than merely being purely academic, recreational, or a novelty. For practicing geometers, understanding this theorem is crucial as it demonstrates the power of projective techniques and provides alternative methods for solving classical construction problems, as well as broader insights.

The practical applications of the Poncelet-Steiner theorem extend beyond pure mathematics. In fields such as computer graphics and computational geometry, it offers efficient algorithms for geometric constructions without the need for more direct and lengthy approaches. This can lead to more streamlined and robust software implementations. Additionally, the theorem has implications in architectural design and engineering, where it can simplify certain drafting and modeling processes, and lending itself to improved design and modeling techniques. Often coordinates may be calculated using a sequence of linear equations, rather than the square roots associated with a circle, enabling faster, more accurate, and more numerically stable computation. In fact, Paul Dirac applied projective geometry in his contribution to the development of quantum mechanics.

Not only does the theorem have historical significance, but it, as well as projective geometry more broadly, also offers deeper insight into the nature of geometric constructions and the relationships between different geometric tools and geometric structures. It challenges conventional thinking about what is necessary for geometric constructions and opens the geometer up to new avenues for problem-solving. Mastering the insights of projective geometry enhances a geometer's ability to approach problems from multiple perspectives, fostering creativity and versatility in their work.

Other types of restricted construction

Restricted constructions involving the compass

''Compass-Only Constructions''

The Poncelet–Steiner theorem can be contrasted with the Mohr–Mascheroni theorem, which states that any compass and straightedge construction can be performed with only a compass. The straightedge is not required but for aesthetic purposes; nothing else is needed in the plane. Constructions carried out using only the compass are often called ''Mascheroni constructions'', or simply ''compass-only constructions''.

'' Rusty Compass ''

The rusty compass restriction allows the use of a compass and straightedge, provided that the compass produces circles of fixed radius. Although the rusty compass constructions were explored since the 10th century, and all of Euclid was shown to be constructable with a rusty compass by the 17th century, the Poncelet-Steiner theorem proves that the rusty compass and straightedge together are more than sufficient for any and all Euclidean construction. Indeed, the rusty compass becomes a tool simplifying constructions over merely the straightedge and single circle. Viewed the other way, the Poncelet-Steiner theorem not only fixes the width of the rusty compass, but ensures that the compass breaks after its first use.

'' Rigid versus Collapsing Compass''

The compass equivalence theorem proves that the rigid compass (also called the modern compass) - one that holds its spacing when lifted from the plane - is equivalent to the traditional collapsing compass (also called divider) - one that does not retain its spacing, thus "resetting to zero", every time it is lifted from the plane. The ability to transfer distances (i.e. construct congruent circles, translate a circle in the plane) - an operation made trivial by the fixable aperture of a rigid compass - was proven by Euclid to be possible with the collapsing compass. Consequently, the rigid compass and the collapsing compass are equivalent; what can be constructed by one can be constructed by the other.

Moreover, circle translation can be done using ''only'' the collapsing compass, without the straightedge tool. Since the compasses are equivalent even in the compass-only construction paradigm, the equivalence is not dependent on the straightedge to supplement the collapsing compass. The equivalence, therefore, is fundamental to the compasses themselves and to the properties of circle geometry. In the compass-only paradigm, additionally, the operation of circle translation requires no more than three additional circles (applications of the compass) over that of the rigid compass, and so it is a trivial matter.

It is valid to point out that the ability to translate circles with a collapsing compass is, in some sense, a purer result. It proves that the operation can be achieved in an abstract way, retained in the geometry of circles, rather than as a feature of a physical tool designed for purpose and transcendent the plane.

Restricted Steiner constructions

The requirement placed on the Poncelet-Steiner theorem - that one circle with its center provided exist in the plane - has been since generalized, or strengthened, to include alternative but equally restrictive conditions.

Other unique scenarios undoubtedly exist than those listed here. This is not an exhaustive list of possibilities.

Poncelet-Steiner without the circle center

In some configurations - or alternative paradigms - the circle center may be omitted entirely, and still all of Euclid remains constructible. In each of the following scenarios, the provided circle(s) are devoid of their centers. The approach to these situations is to construct the circle center from the provided information, leaving a circle with its center in the plane. Thus, these are problems reducible to one that's already been solved by the Poncelet-Steiner theorem. For the most part they are, therefore, geometrically equivalent scenarios; any of these scenarios can produce a circle with its center, and a circle with center is sufficient to construct any of these scenarios by straightedge alone (excepting the arcs of other circles which naturally require a compass)

These scenarios do not contradict Steiner's theorem which, although stating a center is absolutely required, also stipulates by hypothesis that only one circle exists in the plane with no other key information. Thus, a single circle devoid of its center, in the most general of cases, is indeed grossly insufficient to recover the properties, behaviors, and constructive power that the center point provides. With sufficient information, the projective mapping can still be disambiguated. Outlined below is a short list of some of the alternatives that can satisfactorily supplement the center, some of which convert or reduce to one another.

''One Circle Scenarios''

In one of the simplest of alternative scenarios, a single circle is sufficient. It is necessary that two distinct sets of two parallel lines exist in the plane, such that these two sets of two lines are not all mutually parallel, or equivalently, any parallelogram in the plane. Alternatively, we may have only three parallel lines, one being a midline - that is, a middle line equidistant between the other two. Unfortunately for the single-circle cases, a single point or line is grossly insufficient on its own; a parallelogram or equivalent is necessary.

''Two Circle Scenarios''

In another set of alternatives where two circles are provided, it is sufficient that they are either concentric circles, or that they are intersecting. Intersecting circles come in two cases: two intersection points and one intersection point (tangential circles). When concentricity, two points of intersection, or one point of intersection and accompanied tangency, are known properties then sufficient information is provided.

Still other two-circle variations exist. It suffices to have two arbitrary circles in the plane, provided that at least one point is given on either the centerline through them or on their respective radical axis, or provided that no less than a single set of two parallel lines arbitrarily exist in the plane.

Yet other alternatives exist. One may also have, for example, an inscribed-circumscribed quadrilateral: a quadrilateral inscribed in one circle (vertices on the circumference, thus the circle circumscribes the quadrilateral) but the quadrilateral also circumscribes the other circle, thus its edges are tangential to the other circle. In other words, a cyclic quadrilateral to one circle, which is also a tangential quadrilateral to another circle. More generally, the tangential circle need not be interior the circumscribing circle nor interior to the quadrilateral; the edges may be extended infinitely into tangential lines.

''Three Circle Scenarios''

It also suffices, alternatively, to have given three non-intersecting circles, provided they do not all belong to the same coaxial (or coaxal) system of circles - that is, each pair of the three given circles must have a distinct radical axis between them. Three randomly placed circles in the plane almost certainly meet this condition; consequently, and unfortunately, the condition is often not stated with the claim, though it is vital for the purpose of recovering a center point. The condition is guaranteed whenever the three circles do not have collinear centers, or, if they do, are each exterior one another. There are other conditions which guarantee three circles are in different coaxial systems. Otherwise, and in general, it cannot be guaranteed.

''Comment on four or more circles and common radical axes''

There are no quantity of circles, which pairwise share the same radical axis, that can recover a circle center. When in the same coaxial system, any number of circles at all provides no more information than does two circles alone. That is to say, any multiplicity of circles greater than two in the same coaxial system is equivalent to just two in that coaxial system; circles may be reduced (i.e. collapsed, deleted) accordingly and without loss in generality. If in different coaxial systems, three circles are sufficient.

This can be shown from the opposite approach. From any two circles - which naturally define a coaxial system - any number of other circles in the same system may be arbitrarily (effectively) constructed by establishing five or more points on each, using Steiner constructions. Thus two circles implies infinitely many circles. It may be deduced that since two circles alone are insufficient to recover a circle center then so too are three or more circles in the same coaxial system.

Four or more circles (whether or not sharing a coaxial system) only provides convenience; the information they contain is otherwise redundant. Due to this fact, there is no reason to discuss four or more circles; they do not provide an alternative.

Unique alternatives are primarily found among the one and two circle arrangements. Indeed, for three circles within the same coaxial system, something more is necessary; as three circles in this system reduce to two, any supplementary conditions are equivalent to those in the two-circle scenarios. For example, three circles in the same coaxial system could still be satisfied with a single point on the centerline or radical axis.

Poncelet-Steiner without a complete circular arc

''Severi's arc of a circle''

In another alternative, the entire circle is not required at all. In 1904, Francesco Severi proved that any small arc (of the circle), together with the centre, will suffice. This construction breaks the rusty compass at any point before the first circle is completed, but after it has begun, thus drawing some continuous portion of the arc of the circle in the plane, and still all constructions remain possible. Thus, the conditions hypothesizing the Poncelet-Steiner theorem may indeed be weakened, but only with respect to the completeness of the circular arc, and not, per the Steiner theorem, with respect to the center.

The theorem demonstrates the Steiner construction of the intersection points between a line and the circle of an arc. The construction is independent of the size or position of the arc, and uses only a straightedge and the arc.

Moreover, the construction does not make use of the center of the circle of the arc. Though the center is required to complete all of Euclid, as the Steiner theorem proves and the Poncelet-Steiner theorem necessitates, the center is not needed in Severi's construction to intersect a line with the circle of that arc. Using this construction, the arc, and the center of the circle of the arc, all of the above Poncelet-Steiner constructions are equally achievable, albeit with greater difficulty.

Severi's proof illustrates that any arc of the circle fully characterizes the circumference and allows intersection points (of lines) with it to be found. With the inclusion of its center, the entire circle is described. Consequently, the Poncelet-Steiner Theorem's minimum requirement of one circle is still satisfied. The circle remains, fully defined, and fully utilizable, regardless of the absence of some portion of the completed arc. Since Severi's construction intersects lines with the circle of the arc, and the Poncelet-Steiner theorem constructs circle-circle intersections via the straightedge, there is no additional need to justify the circle-circle intersections under this restricted paradigm.

''The arc as it relates to omissions of the circle center''

In each of the previously mentioned scenarios wherein the circle centers are omitted, the completeness of the circular arc is not necessary, as per Severi's theorem. This is because Severi's construction of the intersection points between a line and the circle of an arc does not require the center of said circle. However, in the case of two intersecting circles, their intersection points must be explicitly given whenever arcs of the circle(s) do not exist wherever intersection points do. That is, if the intersection points between two circles of arcs cannot be found directly by way of the two arcs, they must be provided. The completeness of the circular arc is otherwise redundant.

''Defining circle(s) by five points''

It takes five points existing on the curve to minimally describe any unique conic section. With the use of a compass, a circle only requires three such points. Without the use of a compass, like with other conic sections, the circle requires five. The circle may be used (that is, lines may be intersected with it using only Steiner constructions) when it is represented by no fewer than five distinct points on its circumference, provided that a circle or the arc of a circle exist somewhere in the plane. Thus, when provided a circle - with or without its center - or a reduced arc of such a circle, Steiner constructions exist to make use of any other additional circle that is defined by five points on its curve, enabling the construction of additional points on the undrawn circles. Consequently, in any of the previously discussed restricted scenarios involving two or more circles, if all conditions are otherwise met, any circle beyond the first may be substituted by a description in five distinct points. At least one circle must be described either in full or, by Severi's theorem, as an arc.

Control flow restrictions

Though a relatively new concept stemming from computational systems, the notion of control flow and its various restrictions in the context of geometry are also the subject of study. As it applies to the geometrical constructions, these restrictions are typically ones placed on the geometer. As with the case of constructible numbers, prohibitions against arbitrary point placement is one possible control flow restriction, previously discussed in this article. In the aforementioned Mohr-Mascheroni Theorem, restrictions on compass radius could be imposed, such as minimums and maximums given a set of starting points. Other examples may include restrictions on construction sequences and order, decision branching, and repetition or reiteration of steps. Another example of such a restriction is that demonstrated in Pythagorea - a gamified app and website geared toward teaching geometric concepts - in which only the straightedge is used, the geometer has only a set of uniformly-spaced lattice points upon which to begin constructions, and new points can only be constructed through intersections.

Extended, liberated, or neusis constructions

Instead of restricting the rules of construction further, it is of equal interest to study relaxing the restrictions. These are sometimes called ''extended constructions'', because they extend what is constructible by extending the allowable toolset. These constructions can also be called ''neusis constructions'' (from Greek) because they employ tools other than the compass and straightedge, or ''liberated constructions'' because they alleviate the restrictions of the traditional paradigm.

These terms are not necessarily interchangeable or equivalent. Restricting or alleviating the rules of construction alone does not introduce new tools, and some alternative toolsets or additional tools do not necessarily extend the scope of constructibility.

Just as geometers have studied what remains possible to construct (and how) when additional restrictions are placed on traditional construction rules - such as compass only, straightedge only, rusty compass, etc. - they have also studied what constructions becomes possible that weren't already when the natural restrictions inherent to traditional construction rules are alleviated. Questions such as "what becomes constructible", "how might it be constructed", "what are the fewest traditional rules to be broken", "what are the simplest tools needed", "which seemingly different tools are equivalent", "how does the new paradigm simplify traditional constructions", "which traditionally unsolveable problems are equivalent", etc. are asked.

Traditional approaches

The arbitrary angle is not trisectable using traditional compass and straightedge rules, for example, but the trisection becomes constructible when allowed the additional tool of an ellipse in the plane, which is itself not constructible. Some of the traditional unsolved problems such as angle trisection, doubling the cube, squaring the circle, finding cubic roots, etc., since proven to be impossible by straightedge and compass alone, have been resolved using an expanded set of tools. In general, the objects studied to extend the scope of what is constructible have included:
* Non-constructible "auxiliary" curves in the plane - including any of the conic sections, cycloids, lemniscates, limaçons, the Archimedean spiral, Euler spiral, any of the trisectrices or quadratrices, and others.
* Physical tools other than the compass and straightedge - generally called ''neuseis'' (plural) - which include specific tools such as the Tomahawk, markable and double-edged straightedges, graduated rulers, right triangular rulers, linkages, ellipsographs, French curves, and others.

Each of the above categorical approaches have their own unique angle trisection solutions, as do many of the individual tools and curves listed.

The ancient geometers considered the compass and straightedge constructions (known as ''planar constructions'') as ideal and preferred. Second to that they preferred ''solid constructions'', which included the use of conic sections in the plane other than the circle. They favored thirdly the use of arbitrary smooth curves in the plane (such as the Archimedean spiral), and least of all the use of neuseis (alternative physical handheld tools).

The term ''neusis'' (singular) or neusis construction may also refer to a specific tool or method employed by the ancient geometers.

Paper folding

Inspired by Japanese cultural artistry, the mathematical and geometric study of Origami has given rise to a unique approach to geometric construction. There exist various paper-folding techniques whereby folds in paper represent lines.

Lines may be drawn by straightedge or represented by a fold in the paper. Points may be placed by pen or represented as the intersection of lines. Folds may then be made along any line or between any two points. Lines may then be reflected across other lines using paper folds. The Huzita–Hatori axioms establishes the axiomatic basis of paper-folding geometry and the rules which govern this paradigm. In this way, even without a compass, various construction extensions may be achieved, such as, among other things, angle trisection. Through a paper fold, lines and points may be reflected across other lines, through axiomatic methods, offering constructive power that the straightedge in traditional geometry cannot.

Traditional interpretations of paper-folding do not use the compass as there is no way to fold along a curve; though in principle there need not be any prohibitions against the use of a compass because nothing is gained with its use. A compass is unnecessary, serving only as a convenience, because all constructions possible by straightedge and compass are possible by paper-folding alone. Paper-folding is in fact more powerful than traditional geometry, as angle trisections are among the possible constructions.

It is doubtful that the ancient geometers, at least of the western world, ever considered paper folding as a neusis. Understandably this is likely due to the fact that a real sheet of foldable paper is not an idealized plane. The idealized sheet of paper is infinitely large and infinitely foldable.

Not only may paper folding be used to extend constructability and offer alternative approaches to construction, but there exist other practical engineering applications. When provided the mechanical joints and appropriate machinery, folding surfaces may be given functionality, shape, as well as the ability to efficiently store in compact spaces to be deployed later by unfolding. This has particular value in the satellite deployment of orbital telescopes. Se
Space Origami, at JPL, NASA

Metrics, and a comment on the ruler

The graduated ruler is unique in that it defines a metric, and also a norm, and gives rise to the algebraic treatment of geometry, Cartesian graphing, and imports a standard unit for proportionality of segments. The algebraic approach to geometry offers a distinct proof of the Poncelet-Steiner theorem, and the tool is a neusis which enables constructions beyond the traditional compass and straightedge.

Although most mathematicians classify the Euclidean space as a metric space, this is somewhat misleading as no metric is intrinsically defined. This tendency to misclassify may arise from the use of a ruler, a focus on length and distance, or the overlay of a coordinate space. The traditional Euclidean geometric space might more accurately be referred to as a homogeneous space, or a ''geometric space with a set of transformations belonging to an algebraic group'', which enable a discussion on congruence, proportionality, and even angle. This classification is more specific than a topology, an inner-product space, or an affine space, but it is more generalized than a metric space.

Demonstration and relevance

Some algebraic operations performed in the geometric plane, even in traditional geometry, only have meaning in the context of an established field algebra, such as for example the taking of square roots. A segment cannot be square rooted - only numbers can be - thus a segment may only be square rooted if it corresponds to a numeric value (i.e. there exists a field algebra and an isomorphism between real numbers and segments). For clarity, a simple example is this: the square root of a segment may be another segment that is either the same length or a half its length, depending on whether the original is taken as 1 unit or 4 units. Depending on the arbitrary value called "length" that is assigned to a given segment, the length of the segment representing its square root may differ. In traditional geometry without a metric we may discuss proportionality between segments, but not length.

Lengths are meaningless without a metric, and so instead we may consider the ratios between segments. Though it is possible to construct the geometric mean between two segments, this is an exercise in segment ratio (''a'' is to ''g'' as ''g'' is to ''b''); a square root is established when one of these segments (''a'' or ''b'') is decided to be unitary and the other segment, whose proportionality is to the first, represents the real number being square rooted. The segment ratio perspective of traditional Euclidean geometry avoids the establishment of a unit length and therefore a metric. Any construction which aims to take a square root with straightedge and compass requires some standard unit-length segment, even if it is implicit. As such many new constructions become possible whence an isomorphism to the real numbers is established with a field algebra or metric.

A similar limitation exists with products, which is perhaps simpler to visualize. Two segments may not be ''multiplied'' without the metric, though segment ''b'' could be scaled up to ''ab'', this is done by proportionality, if segment ''a'' is first related to a segment ''1'', a unit segment. Without a metric, conversely, a rectangle whose adjacent legs are segments ''a'' and ''b'' contains an area ''ab'', but there is no corresponding segment representation for that area without a metric. It may be noted that addition does not suffer this limitation, as segments may be translated, rotated, and appended to one another without the need for a metric.

Approximations

It is worthwhile to point out that in all construction paradigms, the implicit rule is that all constructions must terminate in a finite number of applications of the available tools (traditionally the compass and straightedge), and produce the exact intended results. It is taken for granted that, from mostly philosophical considerations such as platonic idealism and operationalism, the ancient Greek geometers emphasized finitude and exactness in their constructions. Entire discussions could be made with either of these conditions alleviated.

For any otherwise non-constructible figure:
* It is possible to approximate a construction to a predetermined level of accuracy using only compass and straightedge, using a reiterative approach.
* Exact construction may become possible at the infinite limit of this convergent process, but requires infinite constructions.

For example, an angle trisection may be performed exactly with compass and straightedge, using an infinite sequence of angle bisections. If the construction is terminated at some finite iteration, an accurate approximation of a trisection can be achieved to arbitrary accuracy. Although each point, line or circle is a valid construction, what it aims to approximate can never truly be achieved in finite applications of a compass and/or straightedge.

There are, alternatively, exactly constructible non-iteratively constructed figures that are reasonable approximations for non-constructible figures. For example, there is a relatively simple non-iterative constructions for an approximation of the heptagon. The construction is fairly accurate for most use, and does not constitute an arbitrary termination of an infinite process.

Neuseis as a center point alternative

Using Steiner constructions and a single circle in the plane without its center, the center point may be supplemented (and eventually constructed), and all of Euclid may be constructible, if the straightedge is substituted for any other device (neusis tool) which is capable of drawing arbitrary lines and their parallels (e.g. a markable straightedge, a graduated ruler, a double-edged straightedge).

A tool which may be used to draw lines and their perpendiculars through an arbitrary point, such as set squares or drafting triangles, is also sufficient.

The Cyclos

Some well-studied neuseis tools end up being no more and no less versatile than the compass and/or straightedge, neither extending nor contracting what is constructible. For example, the cyclos, a unique tool in its own right, is similar to the compass in that it draws circles; how it does this is however unique. Although simplifying some constructions, it does so often at the expense of complicating others.

The cyclos refers to a fictional tool postulated for the purposes of testing students' geometric understanding, and has its origins in the modern era for a modern problem. The cyclos is often mistakenly attributed to Euclid, as it was the original Olympiad problem-wording which proposed an alternative history whereby the cyclos was Euclid's tool, though historically Euclid never had such a tool. The tool is only hypothetical - it does not exist - but is valuable as an exercise in abstract geometric thinking. The tool may be simulated in geometry software.

The neusis is capable of drawing the circle according to two properties:
* A circle may be drawn through two diametrically opposite points which define a circle by its diameter (in contrast to two points defining a circle by its radius, for which a standard compass is suitable).
* A circumscribing circle may be drawn through three non-collinear points.

The ''cyclos-only'' paradigm, which prohibits the use of a compass or straightedge, also allows arbitrary point placement on the circle (and in some interpretations the plane, or the line if provided). The intersections of two circles or arcs may be found directly, as is standard geometric practice. If provided, the intersection between two lines or a line and a circle may also be found directly, though the line is generally prohibited in the paradigm.

Ultimately the cyclos is proven to be geometrically equivalent to the compass, and therefore via the Mohr-Mascheroni theorem, all straightedge-compass constructions are possible with the cyclos.

Further generalizations

The Poncelet-Steiner theorem has been generalized to higher dimensions, such as, for example, a three dimensional variation where the straightedge is replaced with a plane, and the circle with center is replaced with a sphere with center. This is essentially a "straightedge only" variation of three dimensional geometry. Though research is ongoing, and some propositions are yet to be proved, many of the properties that apply to the two dimensional case also apply to higher dimensions, as implementations of projective geometry. Additionally, some research is underway to generalize the Poncelet-Steiner theorem to non-Euclidean geometries.

Related theorems

Below is a short list of some theorems of key interest that relate to the Poncelet-Steiner theorem or its variants, to understanding projective geometry, or to the behaviors of straightedges and lines especially as they relate to circles and other conic sections.

*Brianchon's theorem
*Ceva's theorem
*Desargues's theorem
*Menelaus's theorem
*Pascal's theorem
*Poncelet's closure theorem
*Ptolemy's theorem

See also

*Apollonian circles
*Constructible polygon
* Drafting
*Geometric algebra
*Geometric invariant theory
*Geometrography
*Inversive geometry
*Steel square
*T-Square

Notes

References

*
*

Further reading

*
*
*

External links

Jacob Steiner's theorem
at cut-the-knot (It is impossible to find the center of a given circle with the straightedge alone)

Two circles and only a straightedge
an article by Arseniy Akopyan and Roman Fedorov.

A remark on the construction of the centre of a circle by means of the ruler
by Christian Gram.


a page primarily about Steiner's Theorem

Poncelet-Steiner Theorem
(broken link)

The Ruler in Geometrical Constructions
by A. S. Smogorzhevskii.



Poncelet-Steiner Theorem and Dual Billiards
an article by Serge Tabachnikov, from Pennsylvania State University.

Hilbert's Error
an article by Alexander Shen

{{DEFAULTSORT:Poncelet-Steiner theorem
Euclidean plane geometry
Theorems in plane geometry
Straightedge and compass constructions