|
General Position
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the ''general case'' situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings. For example, generically, two lines in the plane intersect in a single point (they are not parallel or coincident). One also says "two generic lines intersect in a point", which is formalized by the notion of a generic point. Similarly, three generic points in the plane are not collinear; if three points are collinear (even stronger, if two coincide), this is a degenerate case. This notion is important in mathematics and its applications, because degenerate cases may require an exceptional treatment; for example, when stating general theorems or giving precise statements thereof, and when writing computer programs (see '' generic co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros. The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscates and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore, other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, ''point'' and ''line'' are primitive entities that are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invertible Sheaf
In mathematics, an invertible sheaf is a coherent sheaf ''S'' on a ringed space ''X'', for which there is an inverse ''T'' with respect to tensor product of ''O''''X''-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle. Due to their interactions with Cartier divisors, they play a central role in the study of algebraic varieties. Definition An invertible sheaf is a locally free sheaf ''S'' on a ringed space ''X'', for which there is an inverse ''T'' with respect to tensor product of ''O''''X''-modules, that is, we have :S \otimes T\ isomorphic to ''O''''X'', which acts as identity element for the tensor product. The most significant cases are those coming from algebraic geometry and complex geometry. For spaces such as (locally) Noetherian schemes or complex manifolds, one can actually replace 'locally free' by 'coherent' in the definition. The invertible sheaves in those theories are in effect the line bundles appropriately form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example, a curve in the plane having a tangent line at each point determines a varying line: the ''tangent bundle'' is a way of organising these. More formally, in algebraic topology and differential topology, a line bundle is defined as a ''vector bundle'' of rank 1. Line bundles are specified by choosing a one-dimensional vector space for each point of the space in a continuous manner. In topological applications, this vector space is usually real or complex. The two cases display fundamentally different behavior because of the different topological properties of real and complex vector spaces: If the origin is removed from the real line, then the result is the set of 1×1 invertible real matrices, which is homotopy-equivalent to a discrete two-point space by contracting the positive and negative reals each to a point; whereas removing the origin from the complex pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sheaf Cohomology
In mathematics, sheaf cohomology is the application of homological algebra to analyze the global sections of a sheaf on a topological space. Broadly speaking, sheaf cohomology describes the obstructions to solving a geometric problem globally when it can be solved locally. The central work for the study of sheaf cohomology is Grothendieck's 1957 Tôhoku paper. Sheaves, sheaf cohomology, and spectral sequences were introduced by Jean Leray at the prisoner-of-war camp Oflag XVII-A in Austria. From 1940 to 1945, Leray and other prisoners organized a "université en captivité" in the camp. Leray's definitions were simplified and clarified in the 1950s. It became clear that sheaf cohomology was not only a new approach to cohomology in algebraic topology, but also a powerful method in complex analytic geometry and algebraic geometry. These subjects often involve constructing global functions with specified local properties, and sheaf cohomology is ideally suited to such probl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor (algebraic Geometry)
In algebraic geometry, divisors are a generalization of codimension-1 subvarieties of algebraic varieties. Two different generalizations are in common use, Cartier divisors and Weil divisors (named for Pierre Cartier and André Weil by David Mumford). Both are derived from the notion of divisibility in the integers and algebraic number fields. Globally, every codimension-1 subvariety of projective space is defined by the vanishing of one homogeneous polynomial; by contrast, a codimension-''r'' subvariety need not be definable by only ''r'' equations when ''r'' is greater than 1. (That is, not every subvariety of projective space is a complete intersection.) Locally, every codimension-1 subvariety of a smooth variety can be defined by one equation in a neighborhood of each point. Again, the analogous statement fails for higher-codimension subvarieties. As a result of this property, much of algebraic geometry studies an arbitrary variety by analysing its codimension-1 subvarietie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cayley–Bacharach Theorem
In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves (plane curves of degree three) in the projective plane . The original form states: :Assume that two cubics and in the projective plane meet in nine (different) points, as they do in general over an algebraically closed field. Then every cubic that passes through any eight of the points also passes through the ninth point. A more intrinsic form of the Cayley–Bacharach theorem reads as follows: :Every cubic curve over an algebraically closed field that passes through a given set of eight points also passes through (counting multiplicities) a ninth point which depends only on . A related result on conics was first proved by the French geometer Michel Chasles and later generalized to cubics by Arthur Cayley and Isaak Bacharach. Details If seven of the points lie on a conic, then the ninth point can be chosen on that conic, since will always contain the whole conic on account of Bézout's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
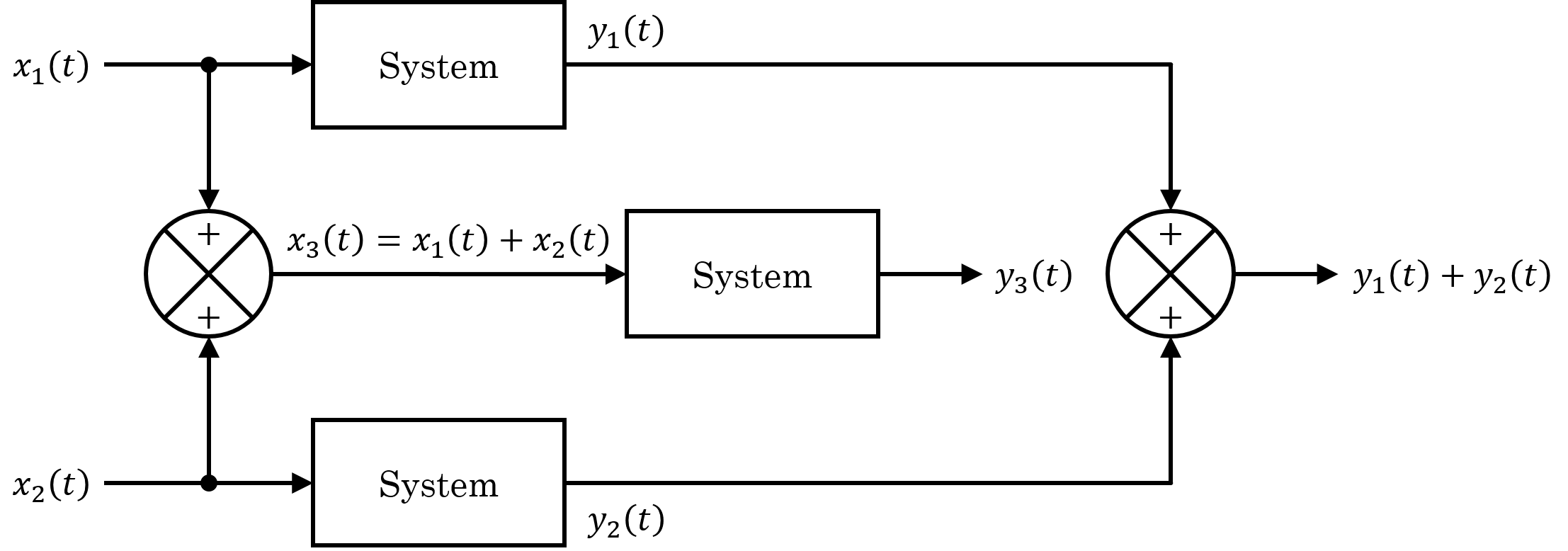
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, that maps an input, as a function of to an output, a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear combin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pencil (mathematics)
In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane. Although the definition of a pencil is rather vague, the common characteristic is that the pencil is completely determined by any two of its members. Analogously, a set of geometric objects that are determined by any three of its members is called a bundle. Thus, the set of all lines through a point in three-space is a bundle of lines, any two of which determine a pencil of lines. To emphasize the two dimensional nature of such a pencil, it is sometimes referred to as a ''flat pencil''. Any geometric object can be used in a pencil. The common ones are lines, planes, circles, conics, spheres, and general curves. Even points can be used. A pencil of points is the set of all points on a given line. A more common term for this set is a ''range'' of points. Pencil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bézout's Theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common zeros of polynomials in indeterminates. In its original form the theorem states that ''in general'' the number of common zeros equals the product of the degrees of the polynomials. It is named after Étienne Bézout. In some elementary texts, Bézout's theorem refers only to the case of two variables, and asserts that, if two plane algebraic curves of degrees d_1 and d_2 have no component in common, they have d_1d_2 intersection points, counted with their multiplicity, and including points at infinity and points with complex coordinates. In its modern formulation, the theorem states that, if is the number of common points over an algebraically closed field of projective hypersurfaces defined by homogeneous polynomials in indeterminates, then is either infinite, or equals the product of the degrees of the polynomials. Moreover, the finite case occurs almost always. In the case of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Veronese Map
In mathematics, the Veronese surface is an algebraic surface in five-dimensional projective space, and is realized by the Veronese embedding, the embedding of the projective plane given by the complete linear system of conics. It is named after Giuseppe Veronese (1854–1917). Its generalization to higher dimension is known as the Veronese variety. The surface admits an embedding in the four-dimensional projective space defined by the projection from a general point in the five-dimensional space. Its general projection to three-dimensional projective space is called a Steiner surface. Definition The Veronese surface is the image of the mapping :\nu:\mathbb^2\to \mathbb^5 given by :\nu: :y:z\mapsto ^2:y^2:z^2:yz:xz:xy/math> where :\cdots/math> denotes homogeneous coordinates. The map \nu is known as the Veronese embedding. Motivation The Veronese surface arises naturally in the study of conics. A conic is a degree 2 plane curve, thus defined by an equation: :Ax^2 + Bxy + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |