Periodogram For Proxima Centauri B on:
[Wikipedia]
[Google]
[Amazon]
In
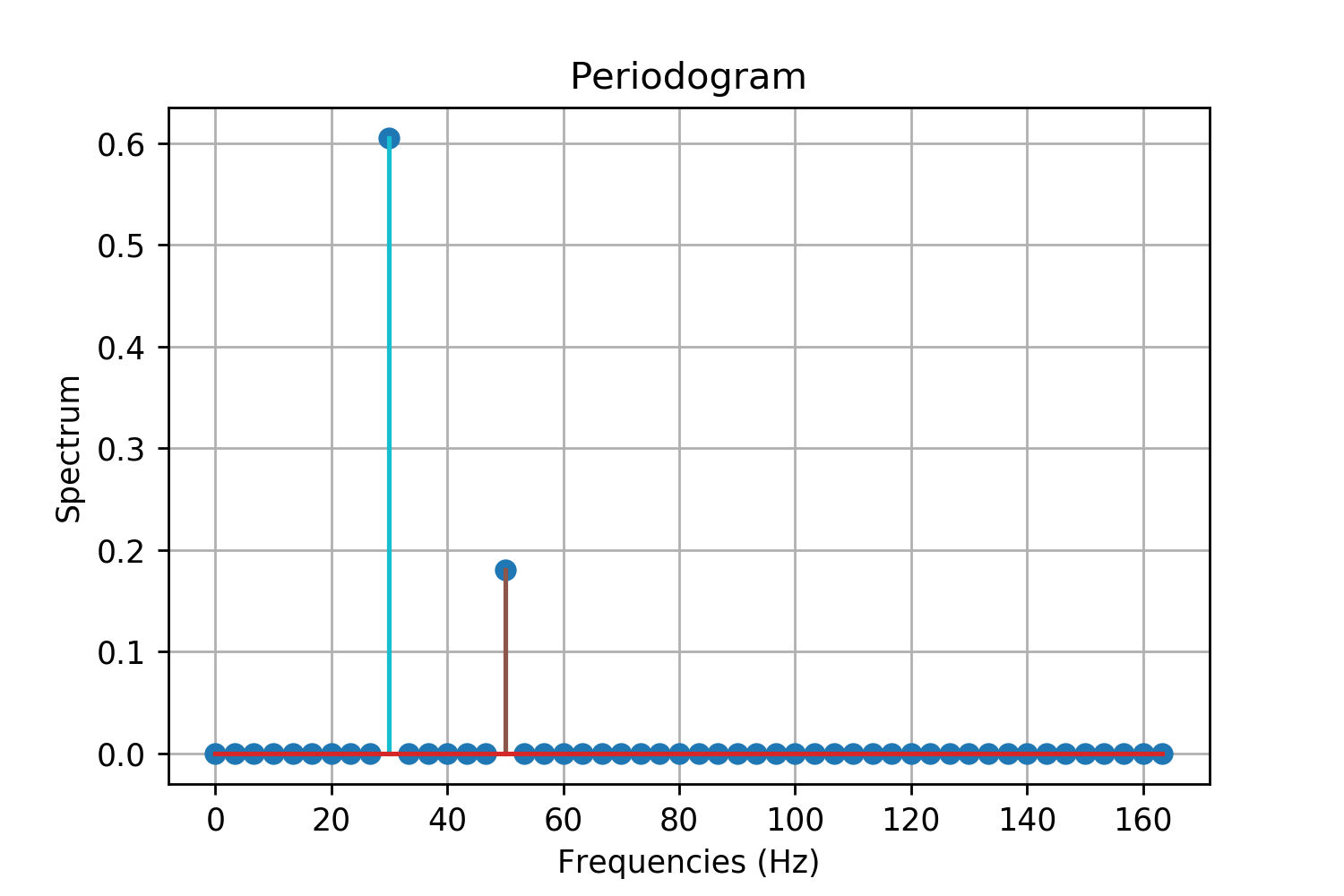
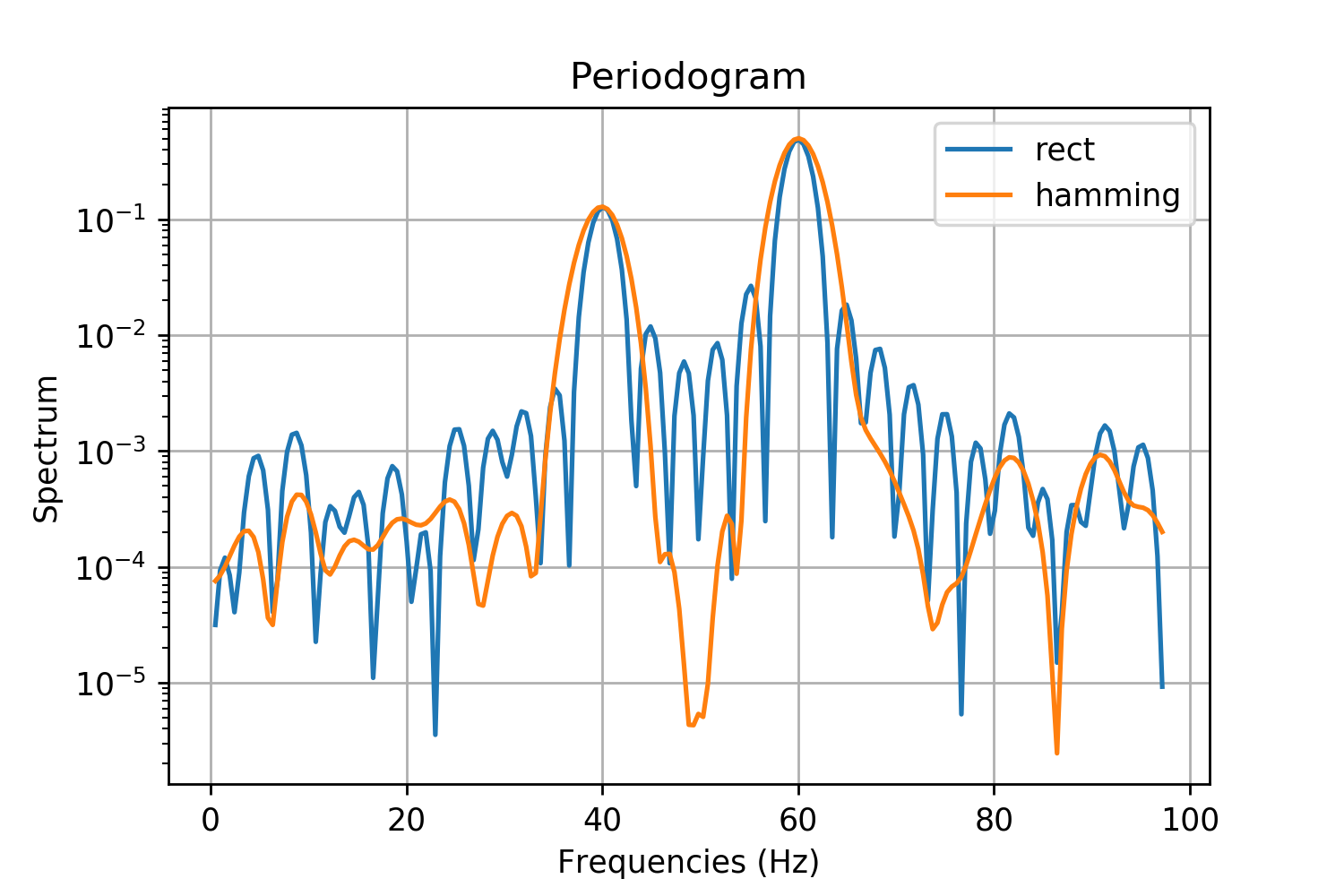 For sufficiently small values of parameter an arbitrarily-accurate approximation for can be observed in the region of the function:
:
which is precisely determined by the samples that span the non-zero duration of (see Discrete-time Fourier transform).
And for sufficiently large values of parameter , can be evaluated at an arbitrarily close frequency by a summation of the form:
:
where is an integer. The periodicity of allows this to be written very simply in terms of a
For sufficiently small values of parameter an arbitrarily-accurate approximation for can be observed in the region of the function:
:
which is precisely determined by the samples that span the non-zero duration of (see Discrete-time Fourier transform).
And for sufficiently large values of parameter , can be evaluated at an arbitrarily close frequency by a summation of the form:
:
where is an integer. The periodicity of allows this to be written very simply in terms of a
 When a periodogram is used to examine the detailed characteristics of an
When a periodogram is used to examine the detailed characteristics of an
signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, ...
, a periodogram is an estimate of the spectral density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, ...
of a signal. The term was coined by Arthur Schuster
Sir Franz Arthur Friedrich Schuster (12 September 1851 – 14 October 1934) was a German-born British physicist known for his work in spectroscopy, electrochemistry, optics, X-radiography and the application of harmonic analysis to physics. ...
in 1898. Today, the periodogram is a component of more sophisticated methods (see spectral estimation). It is the most common tool for examining the amplitude vs frequency characteristics of FIR filter
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse ...
s and window functions. FFT spectrum analyzers are also implemented as a time-sequence of periodograms.
Definition
There are at least two different definitions in use today. One of them involves time-averaging, and one does not. Time-averaging is also the purview of other articles ( Bartlett's method andWelch's method
Welch's method, named after Peter D. Welch, is an approach for spectral density estimation.
It is used in physics, engineering, and applied mathematics for estimating the power of a signal at different frequencies.
The method is based on the ...
). This article is not about time-averaging. The definition of interest here is that the power spectral density of a continuous function, is the Fourier transform of its auto-correlation function (see Cross-correlation theorem, Spectral density#Power spectral density, and Wiener–Khinchin theorem
In applied mathematics, the Wiener–Khinchin theorem or Wiener–Khintchine theorem, also known as the Wiener–Khinchin–Einstein theorem or the Khinchin–Kolmogorov theorem, states that the autocorrelation function of a wide-sense-stationary ...
):
:
Computation

 For sufficiently small values of parameter an arbitrarily-accurate approximation for can be observed in the region of the function:
:
which is precisely determined by the samples that span the non-zero duration of (see Discrete-time Fourier transform).
And for sufficiently large values of parameter , can be evaluated at an arbitrarily close frequency by a summation of the form:
:
where is an integer. The periodicity of allows this to be written very simply in terms of a
For sufficiently small values of parameter an arbitrarily-accurate approximation for can be observed in the region of the function:
:
which is precisely determined by the samples that span the non-zero duration of (see Discrete-time Fourier transform).
And for sufficiently large values of parameter , can be evaluated at an arbitrarily close frequency by a summation of the form:
:
where is an integer. The periodicity of allows this to be written very simply in terms of a Discrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced samples of a function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a comple ...
:
:
where is a periodic summation:
When evaluated for all integers, , between 0 and -1, the array:
:
is a ''periodogram''.
Applications
 When a periodogram is used to examine the detailed characteristics of an
When a periodogram is used to examine the detailed characteristics of an FIR filter
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse ...
or window function
In signal processing and statistics, a window function (also known as an apodization function or tapering function) is a mathematical function that is zero-valued outside of some chosen interval, normally symmetric around the middle of the int ...
, the parameter is chosen to be several multiples of the non-zero duration of the sequence, which is called ''zero-padding'' (see ). When it is used to implement a filter bank, is several sub-multiples of the non-zero duration of the sequence (see ).
One of the periodogram's deficiencies is that the variance at a given frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
does not decrease as the number of samples used in the computation increases. It does not provide the averaging needed to analyze noiselike signals or even sinusoids at low signal-to-noise ratios. Window functions and filter impulse responses are noiseless, but many other signals require more sophisticated methods of spectral estimation. Two of the alternatives use periodograms as part of the process:
*The ''method of averaged periodograms'', more commonly known as Welch's method
Welch's method, named after Peter D. Welch, is an approach for spectral density estimation.
It is used in physics, engineering, and applied mathematics for estimating the power of a signal at different frequencies.
The method is based on the ...
, divides a long x sequence into multiple shorter, and possibly overlapping, subsequences. It computes a windowed periodogram of each one, and computes an array average, i.e. an array where each element is an average of the corresponding elements of all the periodograms. For stationary process
In mathematics and statistics, a stationary process (or a strict/strictly stationary process or strong/strongly stationary process) is a stochastic process whose unconditional joint probability distribution does not change when shifted in time. Con ...
es, this reduces the noise variance of each element by approximately a factor equal to the reciprocal of the number of periodograms.
*Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. In smoothing, the dat ...
is an averaging technique in frequency, instead of time. The smoothed periodogram is sometimes referred to as a ''spectral plot''.
Periodogram-based techniques introduce small biases that are unacceptable in some applications. Other techniques that do not rely on periodograms are presented in the spectral density estimation article.
See also
* Matched filter * Filtered Backprojection (Radon transform) *Welch's method
Welch's method, named after Peter D. Welch, is an approach for spectral density estimation.
It is used in physics, engineering, and applied mathematics for estimating the power of a signal at different frequencies.
The method is based on the ...
* Bartlett's method
* Discrete-time Fourier transform
*Least-squares spectral analysis
Least-squares spectral analysis (LSSA) is a method of estimating a frequency spectrum, based on a least squares fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally ...
, for computing periodograms in data that is not equally spaced
* MUltiple SIgnal Classification (MUSIC), a popular parametric superresolution method
* SAMV
Notes
References
Further reading
* * * {{refend Frequency-domain analysis Fourier analysis