|
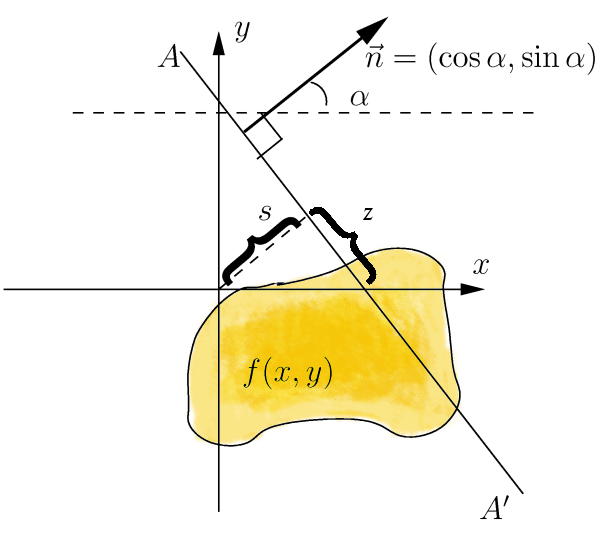
Radon Transform
In mathematics, the Radon transform is the integral transform which takes a function ''f'' defined on the plane to a function ''Rf'' defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes (integrating over lines is known as the X-ray transform). It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object. Explanation If a function f represents an unknown density ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radon Transform
In mathematics, the Radon transform is the integral transform which takes a function ''f'' defined on the plane to a function ''Rf'' defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes (integrating over lines is known as the X-ray transform). It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object. Explanation If a function f represents an unknown density ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in mathematics, as well as in physics, engineering, signal processing and many other fields. Formulation Its most basic form as a function of time (''t'') is: y(t) = A\sin(2 \pi f t + \varphi) = A\sin(\omega t + \varphi) where: * ''A'', ''amplitude'', the peak deviation of the function from zero. * ''f'', '' ordinary frequency'', the ''number'' of oscillations (cycles) that occur each second of time. * ''ω'' = 2''f'', '' angular frequency'', the rate of change of the function argument in units of radians per second. * \varphi, '' phase'', specifies (in radians) where in its cycle the oscillation is at ''t'' = 0. When \varphi is non-zero, the entire waveform appears to be shifted in time by the amount ''φ''/''ω'' seconds. A negative val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure (mathematics)
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures ( length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general. The intuition behind this concept dates back to ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypersurface
In geometry, a hypersurface is a generalization of the concepts of hyperplane, plane curve, and surface. A hypersurface is a manifold or an algebraic variety of dimension , which is embedded in an ambient space of dimension , generally a Euclidean space, an affine space or a projective space. Hypersurfaces share, with surfaces in a three-dimensional space, the property of being defined by a single implicit equation, at least locally (near every point), and sometimes globally. A hypersurface in a (Euclidean, affine, or projective) space of dimension two is a plane curve. In a space of dimension three, it is a surface. For example, the equation :x_1^2+x_2^2+\cdots+x_n^2-1=0 defines an algebraic hypersurface of dimension in the Euclidean space of dimension . This hypersurface is also a smooth manifold, and is called a hypersphere or an -sphere. Smooth hypersurface A hypersurface that is a smooth manifold is called a ''smooth hypersurface''. In , a smooth hypersurf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its '' ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. This notion can be used in any general space in which the concept of the dimension of a subspace is defined. In different settings, hyperplanes may have different properties. For instance, a hyperplane of an -dimensional affine space is a flat subset with dimension and it separates the space into two half spaces. While a hyperplane of an -dimensional projective space does not have this property. The difference in dimension between a subspace and its ambient space is known as the codimension of with respect to . Therefore, a necessary and sufficient condition for to be a hyperplane in is for to have codimension one in . Technical description In geometry, a hyperplane of an ''n''-di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms ''path integral'', ''curve integral'', and ''curvilinear integral'' are also used; '' contour integral'' is used as well, although that is typically reserved for line integrals in the complex plane. The function to be integrated may be a scalar field or a vector field. The value of the line integral is the sum of values of the field at all points on the curve, weighted by some scalar function on the curve (commonly arc length or, for a vector field, the scalar product of the vector field with a differential vector in the curve). This weighting distinguishes the line integral from simpler integrals defined on intervals. Many simple formulae in physics, such as the definition of work as W=\mathbf\cdot\mathbf, have natural continuous analogues in terms of line integrals, in this case \textstyle W = \int_L \mathbf(\mathbf)\cdot d\mathbf, which computes the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection Seismology
Reflection seismology (or seismic reflection) is a method of exploration geophysics that uses the principles of seismology to estimate the properties of the Earth's subsurface from reflected seismic waves. The method requires a controlled seismic source of energy, such as dynamite or Tovex blast, a specialized air gun or a seismic vibrator. Reflection seismology is similar to sonar and echolocation. This article is about surface seismic surveys; for vertical seismic profiles, see VSP. History Reflections and refractions of seismic waves at geologic interfaces within the Earth were first observed on recordings of earthquake-generated seismic waves. The basic model of the Earth's deep interior is based on observations of earthquake-generated seismic waves transmitted through the Earth's interior (e.g., Mohorovičić, 1910). The use of human-generated seismic waves to map in detail the geology of the upper few kilometers of the Earth's crust followed shortly thereafter and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Protein Complex
A protein complex or multiprotein complex is a group of two or more associated polypeptide chains. Protein complexes are distinct from multienzyme complexes, in which multiple catalytic domains are found in a single polypeptide chain. Protein complexes are a form of quaternary structure. Proteins in a protein complex are linked by non-covalent protein–protein interactions. These complexes are a cornerstone of many (if not most) biological processes. The cell is seen to be composed of modular supramolecular complexes, each of which performs an independent, discrete biological function. Through proximity, the speed and selectivity of binding interactions between enzymatic complex and substrates can be vastly improved, leading to higher cellular efficiency. Many of the techniques used to enter cells and isolate proteins are inherently disruptive to such large complexes, complicating the task of determining the components of a complex. Examples of protein complexes include th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virus
A virus is a wikt:submicroscopic, submicroscopic infectious agent that replicates only inside the living Cell (biology), cells of an organism. Viruses infect all life forms, from animals and plants to microorganisms, including bacteria and archaea. Since Dmitri Ivanovsky's 1892 article describing a non-bacterial pathogen infecting tobacco plants and the discovery of the tobacco mosaic virus by Martinus Beijerinck in 1898,Dimmock p. 4 more than 9,000 virus species have been described in detail of the millions of types of viruses in the environment. Viruses are found in almost every ecosystem on Earth and are the most numerous type of biological entity. The study of viruses is known as virology, a subspeciality of microbiology. When infected, a host cell is often forced to rapidly produce thousands of copies of the original virus. When not inside an infected cell or in the process of infecting a cell, viruses exist in the form of independent particles, or ''virions'', consisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Macromolecular Assemblies
The term macromolecular assembly (MA) refers to massive chemical structures such as viruses and non-biologic nanoparticles, cellular organelles and membranes and ribosomes, etc. that are complex mixtures of polypeptide, polynucleotide, polysaccharide or other polymeric macromolecules. They are generally of more than one of these types, and the mixtures are defined spatially (i.e., with regard to their chemical shape), and with regard to their underlying chemical composition and structure. Macromolecules are found in living and nonliving things, and are composed of many hundreds or thousands of atoms held together by covalent bonds; they are often characterized by repeating units (i.e., they are polymers). Assemblies of these can likewise be biologic or non-biologic, though the MA term is more commonly applied in biology, and the term supramolecular assembly is more often applied in non-biologic contexts (e.g., in supramolecular chemistry and nanotechnology). MAs of macromolecu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |