Periodic Points Of Complex Quadratic Mappings

This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.

These periodic points play a role in the theories of Fatou and Julia sets.

Definitions

Let

:$f_c(z) = z^2+c\,$

be the complex quadric mapping, where $z$ and $c$ are complex numbers.

Notationally, $f^ _c (z)$ is the $k$-fold composition of $f_c$ with itself (not to be confused with the $k$th derivative of $f_c$)—that is, the value after the ''k''-th iteration of the function $f _c.$ Thus

:$f^ _c (z) = f_c(f^ _c (z)).$

Periodic points of a complex quadratic mapping of period $p$ are points $z$ of the dynamical plane such that

:$f^ _c (z) = z,$

where $p$ is the smallest positive integer for which the equation holds at that ''z''.

We can introduce a new function:

:$F_p(z,f) = f^ _c (z) - z,$

so periodic points are zeros of function $F_p(z,f)$: points ''z'' satisfying

:$F_p(z,f) = 0,$

which is a polynomial of degree $2^p.$

Number of periodic points

The degree of the polynomial $F_p(z,f)$ describing periodic points is $d = 2^p$ so it has exactly $d = 2^p$ complex roots (= periodic points), counted with multiplicity.

Stability of periodic points (orbit) - multiplier

The multiplier (or eigenvalue, derivative) $m(f^p,z_0)=\lambda$ of a rational map $f$ iterated $p$ times at cyclic point $z_0$ is defined as:

:$m(f^p,z_0) = \lambda = \begin f^(z_0), &\mboxz_0 \ne \infty \\ \frac, & \mboxz_0 = \infty \end$

where $f^ (z_0)$ is the first derivative of $f^p$ with respect to $z$ at $z_0$.

Because the multiplier is the same at all periodic points on a given orbit, it is called a multiplier of the periodic orbit.

The multiplier is:
*a complex number;
*invariant under conjugation of any rational map at its fixed point;
*used to check stability of periodic (also fixed) points with stability index $abs(\lambda). \,$

A periodic point is
* attracting when $abs(\lambda) < 1;$
** super-attracting when $abs(\lambda) = 0;$
** attracting but not super-attracting when $0 < abs(\lambda) < 1;$
* indifferent when $abs(\lambda) = 1;$
** rationally indifferent or parabolic if $\lambda$ is a root of unity;
** irrationally indifferent if $abs(\lambda)=1$ but multiplier is not a root of unity;
* repelling when $abs(\lambda) > 1.$

Periodic points
* that are attracting are always in the Fatou set;
* that are repelling are in the Julia set;
* that are indifferent fixed points may be in one or the other. A parabolic periodic point is in the Julia set.

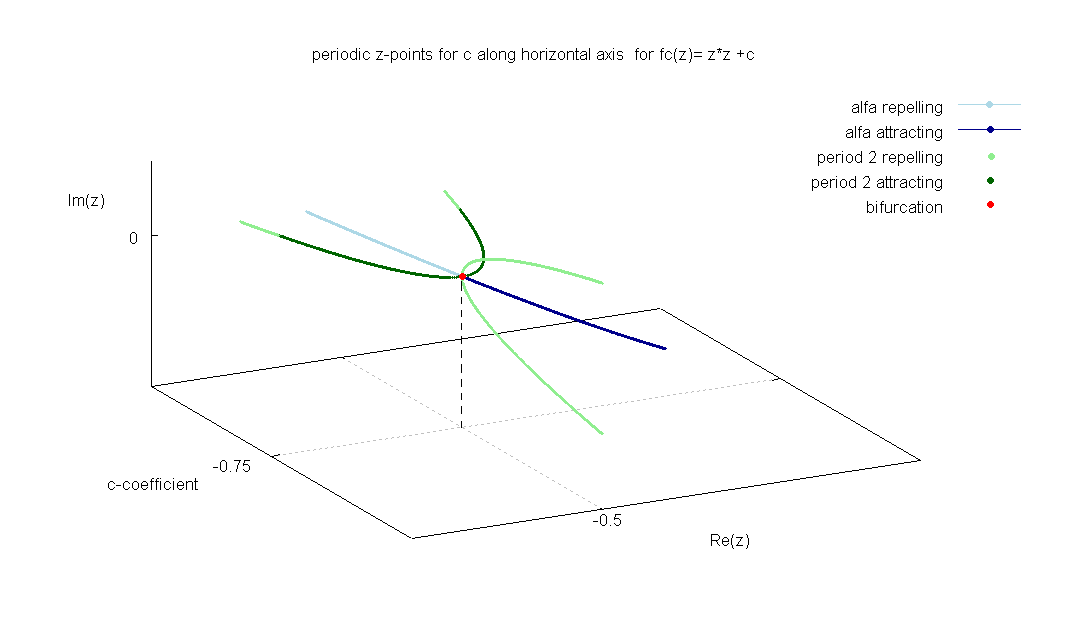
Period-1 points (fixed points)

Finite fixed points

Let us begin by finding all finite points left unchanged by one application of $f$. These are the points that satisfy $f_c(z)=z$. That is, we wish to solve

: $z^2+c=z,\,$

which can be rewritten as

: $\ z^2-z+c=0.$

Since this is an ordinary quadratic equation in one unknown, we can apply the standard quadratic solution formula:

: $\alpha_1 = \frac$ and $\alpha_2 = \frac.$
So for $c \in \mathbb \setminus \$ we have two finite fixed points $\alpha_1$ and $\alpha_2$.

Since
: $\alpha_1 = \frac-m$ and $\alpha_2 = \frac+m$ where $m = \frac,$

we have $\alpha_1 + \alpha_2 = 1$.

Thus fixed points are symmetrical about $z = 1/2$.

Complex dynamics

Here different notation is commonly used:

:$\alpha_c = \frac$ with multiplier $\lambda_ = 1-\sqrt$

and

:$\beta_c = \frac$ with multiplier $\lambda_ = 1+\sqrt.$

Again we have

:$\alpha_c + \beta_c = 1 .$

Since the derivative with respect to ''z'' is

:$P_c'(z) = \fracP_c(z) = 2z ,$

we have

:$P_c'(\alpha_c) + P_c'(\beta_c)= 2 \alpha_c + 2 \beta_c = 2 (\alpha_c + \beta_c) = 2 .$

This implies that $P_c$ can have at most one attractive fixed point.

These points are distinguished by the facts that:
* $\beta_c$ is:
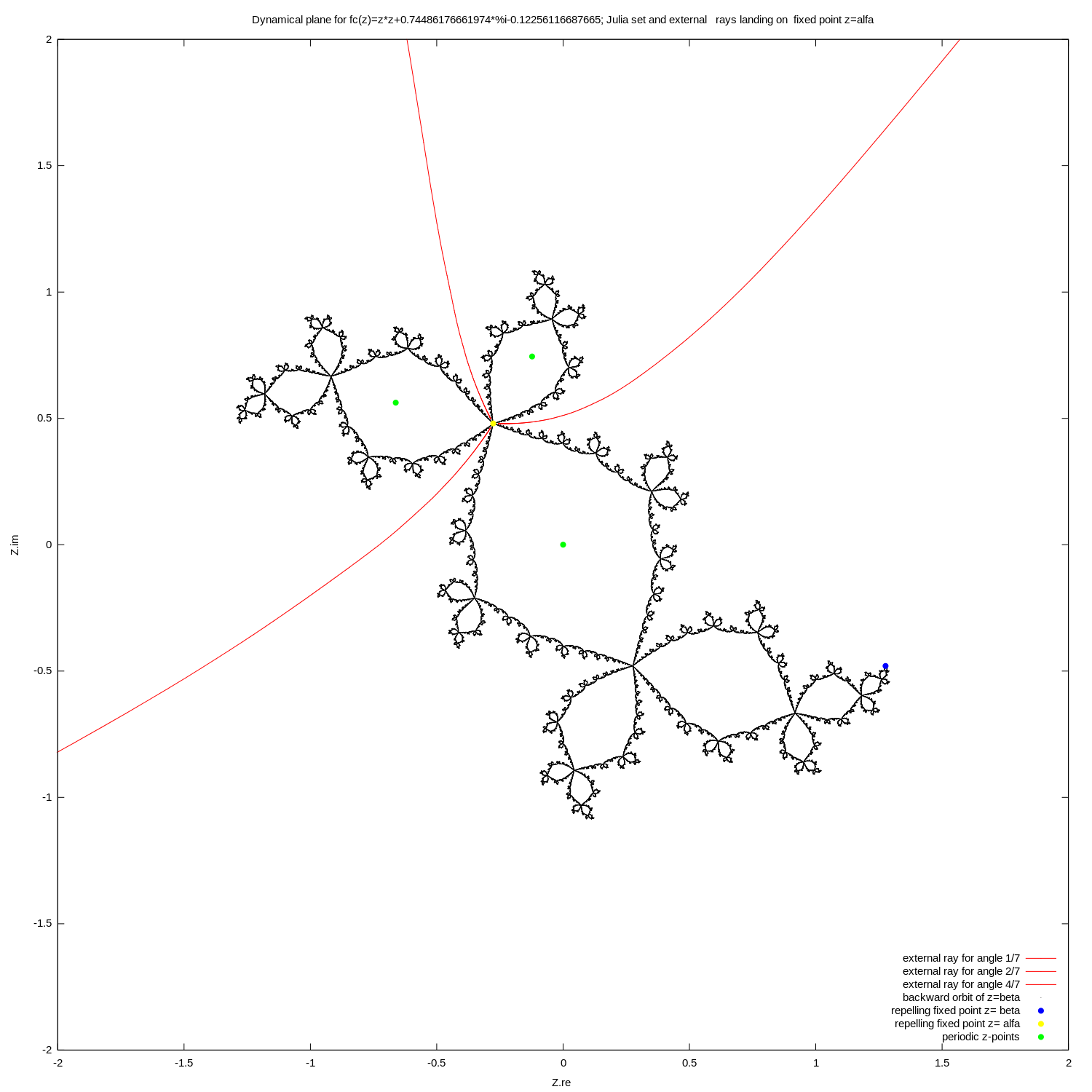
**the landing point of the external ray for angle=0 for $c \in M \setminus \left\$
**the most repelling fixed point of the Julia set
** the one on the right (whenever fixed point are not symmetrical around the real axis), it is the extreme right point for connected Julia sets (except for cauliflower).
* $\alpha_c$ is:
** the landing point of several rays
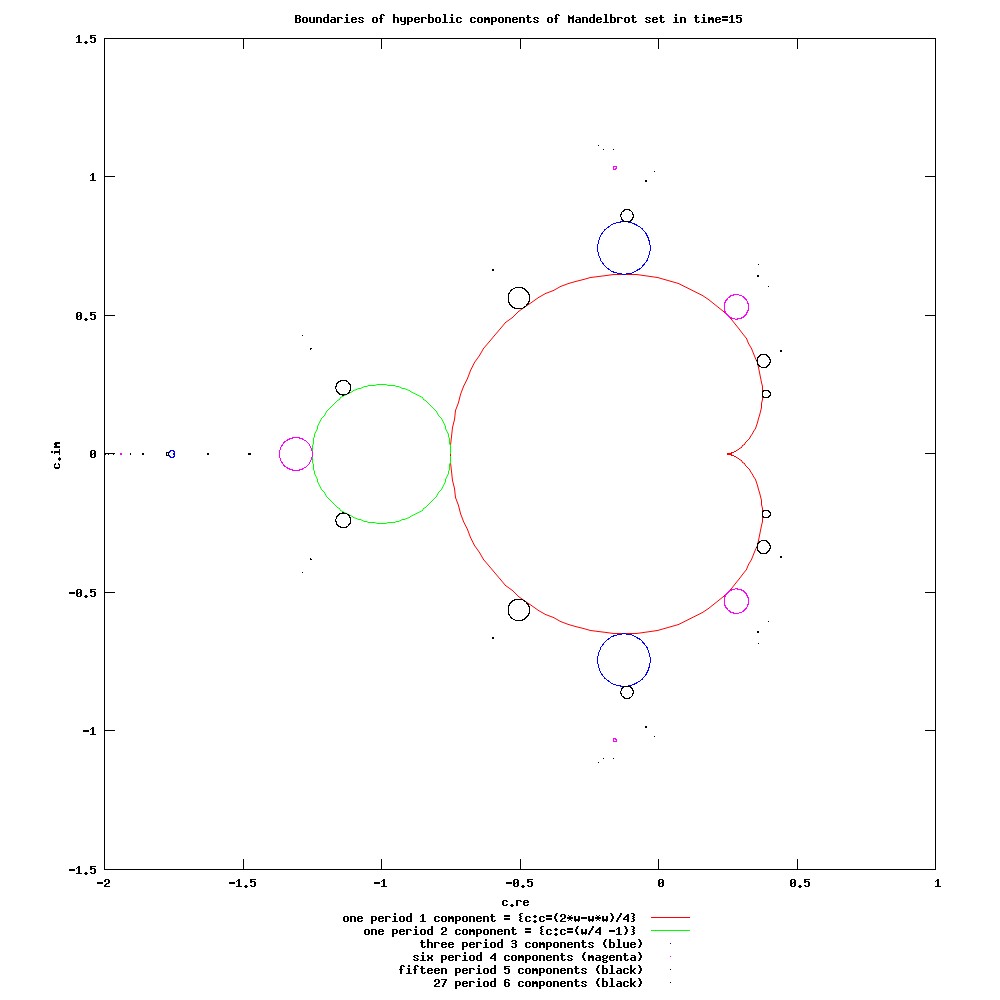
**attracting when $c$ is in the main cardioid of the Mandelbrot set, in which case it is in the interior of a filled-in Julia set, and therefore belongs to the Fatou set (strictly to the basin of attraction of finite fixed point)
**parabolic at the root point of the limb of the Mandelbrot set
**repelling for other values of $c$

Special cases

An important case of the quadratic mapping is $c=0$. In this case, we get $\alpha_1 = 0$ and $\alpha_2=1$. In this case, 0 is a superattractive fixed point, and 1 belongs to the Julia set.

Only one fixed point

We have $\alpha_1=\alpha_2$ exactly when $1-4c=0.$ This equation has one solution, $c=1/4,$ in which case $\alpha_1=\alpha_2=1/2$. In fact $c=1/4$ is the largest positive, purely real value for which a finite attractor exists.

Infinite fixed point

We can extend the complex plane $\mathbb$ to the Riemann sphere (extended complex plane) $\mathbb$ by adding infinity:

:$\mathbb = \mathbb \cup \$

and extend $f_c$ such that $f_c(\infty)=\infty.$

Then infinity is:
*superattracting
*a fixed point of $f_c$:$f_c(\infty)=\infty=f^_c(\infty).$

Period-2 cycles

Period-2 cycles are two distinct points $\beta_1$ and $\beta_2$ such that $f_c(\beta_1) = \beta_2$ and $f_c(\beta_2) = \beta_1$, and hence

:$f_c(f_c(\beta_n)) = \beta_n$

for $n \in \$:

:$f_c(f_c(z)) = (z^2+c)^2+c = z^4 + 2cz^2 + c^2 + c.$

Equating this to ''z'', we obtain

:$z^4 + 2cz^2 - z + c^2 + c = 0.$

This equation is a polynomial of degree 4, and so has four (possibly non-distinct) solutions. However, we already know two of the solutions. They are $\alpha_1$ and $\alpha_2$, computed above, since if these points are left unchanged by one application of $f$, then clearly they will be unchanged by more than one application of $f$.

Our 4th-order polynomial can therefore be factored in 2 ways:

First method of factorization

: $(z-\alpha_1)(z-\alpha_2)(z-\beta_1)(z-\beta_2) = 0.\,$

This expands directly as $x^4 - Ax^3 + Bx^2 - Cx + D = 0$ (note the alternating signs), where

: $D = \alpha_1 \alpha_2 \beta_1 \beta_2, \,$

: $C = \alpha_1 \alpha_2 \beta_1 + \alpha_1 \alpha_2 \beta_2 + \alpha_1 \beta_1 \beta_2 + \alpha_2 \beta_1 \beta_2, \,$

: $B = \alpha_1 \alpha_2 + \alpha_1 \beta_1 + \alpha_1 \beta_2 + \alpha_2 \beta_1 + \alpha_2 \beta_2 + \beta_1 \beta_2, \,$

: $A = \alpha_1 + \alpha_2 + \beta_1 + \beta_2.\,$

We already have two solutions, and only need the other two. Hence the problem is equivalent to solving a quadratic polynomial. In particular, note that

: $\alpha_1 + \alpha_2 = \frac + \frac = \frac = 1$

and

: $\alpha_1 \alpha_2 = \frac = \frac= \frac = \frac = c.$

Adding these to the above, we get $D = c \beta_1 \beta_2$ and $A = 1 + \beta_1 + \beta_2$. Matching these against the coefficients from expanding $f$, we get

: $D = c \beta_1 \beta_2 = c^2 + c$ and $A = 1 + \beta_1 + \beta_2 = 0.$

From this, we easily get

:$\beta_1 \beta_2 = c + 1$ and $\beta_1 + \beta_2 = -1$.

From here, we construct a quadratic equation with $A' = 1, B = 1, C = c+1$ and apply the standard solution formula to get

: $\beta_1 = \frac$ and $\beta_2 = \frac.$

Closer examination shows that:

:$f_c(\beta_1) = \beta_2$ and $f_c(\beta_2) = \beta_1,$

meaning these two points are the two points on a single period-2 cycle.

Second method of factorization

We can factor the quartic by using polynomial long division to divide out the factors $(z-\alpha_1)$ and $(z-\alpha_2),$ which account for the two fixed points $\alpha_1$ and $\alpha_2$ (whose values were given earlier and which still remain at the fixed point after two iterations):

:$(z^2+c)^2 + c -z = (z^2 + c - z)(z^2 + z + c +1 ). \,$

The roots of the first factor are the two fixed points. They are repelling outside the main cardioid.

The second factor has the two roots

:$\frac. \,$

These two roots, which are the same as those found by the first method, form the period-2 orbit.

Special cases

Again, let us look at $c=0$. Then

: $\beta_1 = \frac$ and $\beta_2 = \frac,$

both of which are complex numbers. We have $, \beta_1 , = , \beta_2 , = 1$. Thus, both these points are "hiding" in the Julia set.
Another special case is $c=-1$, which gives $\beta_1 = 0$ and $\beta_2 = -1$. This gives the well-known superattractive cycle found in the largest period-2 lobe of the quadratic Mandelbrot set.

Cycles for period greater than 2

The degree of the equation $f^(z)=z$ is 2^''n''; thus for example, to find the points on a 3-cycle we would need to solve an equation of degree 8. After factoring out the factors giving the two fixed points, we would have a sixth degree equation.

There is no general solution in radicals to polynomial equations of degree five or higher, so the points on a cycle of period greater than 2 must in general be computed using numerical methods. However, in the specific case of period 4 the cyclical points have lengthy expressions in radicals.Gvozden Rukavina : Quadratic recurrence equations - exact explicit solution of period four fixed points functions in bifurcation diagram
/ref>

In the case ''c'' = –2, trigonometric solutions exist for the periodic points of all periods. The case $z_=z_n^2-2$ is equivalent to the logistic map case ''r'' = 4: $x_=4x_n(1-x_n).$ Here the equivalence is given by $z=2-4x.$ One of the ''k''-cycles of the logistic variable ''x'' (all of which cycles are repelling) is

:$\sin^2\left(\frac\right), \, \sin^2\left(2\cdot\frac\right), \, \sin^2\left(2^2\cdot\frac\right), \, \sin^2\left(2^3\cdot\frac\right), \dots , \sin^2\left(2^\frac\right).$

References

Further reading

* Geometrical properties of polynomial roots
*Alan F. Beardon, Iteration of Rational Functions, Springer 1991,
*Michael F. Barnsley (Author), Stephen G. Demko (Editor), Chaotic Dynamics and Fractals (Notes and Reports in Mathematics in Science and Engineering Series) Academic Pr (April 1986),
Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002 The permutations of periodic points in quadratic polynominials by J Leahy

External links

* ttp://www.mrob.com/pub/muency/brownmethod.html ''Brown Method'' by Robert P. Munafobr>arXiv:hep-th/0501235v2
V.Dolotin, A.Morozov: ''Algebraic Geometry of Discrete Dynamics''. The case of one variable.

{{DEFAULTSORT:Periodic Points Of Complex Quadratic Mappings
Complex dynamics
Fractals
Limit sets