|
Logistic Map
The logistic map is a discrete dynamical system defined by the quadratic difference equation: Equivalently it is a recurrence relation and a polynomial mapping of degree 2. It is often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple nonlinear dynamical equations. The map was initially utilized by Edward Lorenz in the 1960s to showcase properties of irregular solutions in climate systems. It was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Other researchers who have contributed to the study of the logistic map include Stanisław Ulam, John von Neumann, Pekka Myrberg, Oleksandr Sharkovsky, Nicholas Metropolis, and Mitchell Feigenbaum. Two introductory examples Dynamical Systems example In the logistic map, x is a variable, and r is a parameter. It is a map in the sense that it map ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nicholas Metropolis
Nicholas Constantine Metropolis (Greek: ; June 11, 1915 – October 17, 1999) was a Greek-American physicist. Metropolis received his BSc (1937) and PhD in physics (1941, with Robert Mulliken) at the University of Chicago. Shortly afterwards, Robert Oppenheimer recruited him from Chicago, where he was collaborating with Enrico Fermi and Edward Teller on the first nuclear reactors, to the Los Alamos National Laboratory. He arrived in Los Alamos in April 1943, as a member of the original staff of fifty scientists. He came back to Los Alamos in 1948 to lead the group in the Theoretical Division that designed and built the MANIAC I computer in 1952 that was modeled on the IAS machine, and the MANIAC II in 1957. Early life and education Nicolas Metropolis was born on June 11, 1915, in Chicago, US. Metropolis received his BSc (1936) and PhD in chemical physics (1941) at the University of Chicago. During his PhD he worked with Robert Mulliken. After graduation, he worked as an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Population
Population is a set of humans or other organisms in a given region or area. Governments conduct a census to quantify the resident population size within a given jurisdiction. The term is also applied to non-human animals, microorganisms, and plants, and has specific uses within such fields as ecology and genetics. Etymology The word ''population'' is derived from the Late Latin ''populatio'' (a people, a multitude), which itself is derived from the Latin word ''populus'' (a people). Use of the term Social sciences In sociology and population geography, population refers to a group of human beings with some predefined feature in common, such as location, Race (human categorization), race, ethnicity, nationality, or religion. Ecology In ecology, a population is a group of organisms of the same species which inhabit the same geographical area and are capable of Sexual reproduction, interbreeding. The area of a sexual population is the area where interbreeding is possi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mandelbrot Set
The Mandelbrot set () is a two-dimensional set (mathematics), set that is defined in the complex plane as the complex numbers c for which the function f_c(z)=z^2+c does not Stability theory, diverge to infinity when Iteration, iterated starting at z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value. This set was first defined and drawn by Robert W. Brooks and Peter Matelski in 1978, as part of a study of Kleinian groups. Afterwards, in 1980, Benoit Mandelbrot obtained high-quality visualizations of the set while working at IBM's Thomas J. Watson Research Center in Yorktown Heights, New York. Images of the Mandelbrot set exhibit an infinitely complicated Boundary (topology), boundary that reveals progressively ever-finer Recursion, recursive detail at increasing magnifications; mathematically, the boundary of the Mandelbrot set is a ''fractal curve''. The "style" of this recursive detail depends on the region of the set boundary being ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
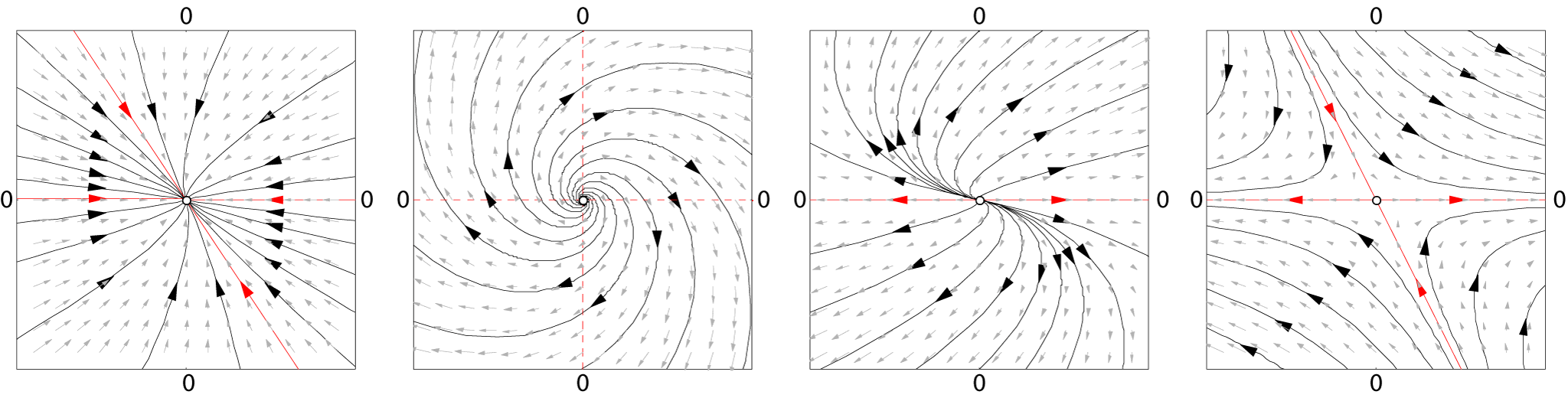
Fixed Point (mathematics)
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation (mathematics), transformation. Specifically, for function (mathematics), functions, a fixed point is an element that is mapped to itself by the function. Any set of fixed points of a transformation is also an invariant set. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain of a function, domain and the codomain of , and . In particular, cannot have any fixed point if its domain is disjoint from its codomain. If is defined on the real numbers, it corresponds, in graphical terms, to a curve in the Euclidean plane, and each fixed-point corresponds to an intersection of the curve with the line , cf. picture. For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime. He has further been called "the Carl Friedrich Gauss, Gauss of History of mathematics, modern mathematics". Due to his success in science, along with his influence and philosophy, he has been called "the philosopher par excellence of modern science". As a mathematician and physicist, he made many original fundamental contributions to Pure mathematics, pure and applied mathematics, mathematical physics, and celestial mechanics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. Poincaré is regarded as the cr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter "M" first and "Y" last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Aperiodic
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called ''aperiodic''. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orbit (dynamics)
In mathematics, specifically in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. It can be understood as the subset of phase space covered by the trajectory of the dynamical system under a particular set of initial conditions, as the system evolves. As a phase space trajectory is uniquely determined for any given set of phase space coordinates, it is not possible for different orbits to intersect in phase space, therefore the set of all orbits of a dynamical system is a partition of the phase space. Understanding the properties of orbits by using topological methods is one of the objectives of the modern theory of dynamical systems. For discrete-time dynamical systems, the orbits are sequences; for real dynamical systems, the orbits are curves; and for holomorphic dynamical systems, the orbits are Riemann surfaces. Definition Given a dynamical system (''T'', ''M'', Φ) with ''T'' a group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |