Pendulum Phase Portrait

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing.

From the first scientific investigations of the pendulum around 1602 by Galileo Galilei, the regular motion of pendulums was used for timekeeping and was the world's most accurate timekeeping technology until the 1930s. The pendulum clock invented by Christiaan Huygens in 1658 became the world's standard timekeeper, used in homes and offices for 270 years, and achieved accuracy of about one second per year before it was superseded as a time standard by the quartz clock in the 1930s. Pendulums are also used in scientific instruments such as accelerometers and seismometers. Historically they were used as gravimeters to measure the acceleration of gravity in geo-physical surveys, and even as a standard of length. The word ''pendulum'' is new Latin, from the Latin ''pendulus'', meaning ''hanging''.

Simple gravity pendulum

The ''simple gravity pendulum'' is an idealized mathematical model of a pendulum. This is a weight (or bob) on the end of a massless cord suspended from a pivot, without friction. When given an initial push, it will swing back and forth at a constant amplitude. Real pendulums are subject to friction and air drag, so the amplitude of their swings declines.

Period of oscillation

The period of swing of a simple gravity pendulum depends on its length, the local strength of gravity, and to a small extent on the maximum angle that the pendulum swings away from vertical, ''θ''₀, called the amplitude., p.188-194 It is independent of the mass of the bob. If the amplitude is limited to small swings,A "small" swing is one in which the angle is small enough that can be approximated by when is measured in radians the period of a simple pendulum, the time taken for a complete cycle, is:

where $L$ is the length of the pendulum and $g$ is the local acceleration of gravity.

For small swings the period of swing is approximately the same for different size swings: that is, ''the period is independent of amplitude''. This property, called isochronism, is the reason pendulums are so useful for timekeeping. Successive swings of the pendulum, even if changing in amplitude, take the same amount of time.

For larger amplitudes, the period increases gradually with amplitude so it is longer than given by equation (1). For example, at an amplitude of ''θ''₀ = 0.4 radians (23°) it is 1% larger than given by (1). The period increases asymptotically (to infinity) as ''θ''₀ approaches π radians (180°), because the value ''θ''₀ = π is an unstable equilibrium point for the pendulum. The true period of an ideal simple gravity pendulum can be written in several different forms (see pendulum (mathematics)), one example being the infinite series:
T =
2\pi \sqrt \left \sum_^\infty \left( \frac \right)^2 \sin^ \left(\frac\right) \right=
2\pi \sqrt \left( 1 + \frac\theta_0^2 + \frac\theta_0^4 + \cdots \right)

where $\theta_0$ is in radians.

The difference between this true period and the period for small swings (1) above is called the ''circular error''. In the case of a typical grandfather clock whose pendulum has a swing of 6° and thus an amplitude of 3° (0.05 radians), the difference between the true period and the small angle approximation (1) amounts to about 15 seconds per day.

For small swings the pendulum approximates a harmonic oscillator, and its motion as a function of time, ''t'', is approximately simple harmonic motion:
$\theta (t) = \theta_0 \cos \left( \frac\, t +\varphi \right)$
where $\varphi$ is a constant value, dependent on initial conditions.

For real pendulums, the period varies slightly with factors such as the buoyancy and viscous resistance of the air, the mass of the string or rod, the size and shape of the bob and how it is attached to the string, and flexibility and stretching of the string. In precision applications, corrections for these factors may need to be applied to eq. (1) to give the period accurately.

Compound pendulum

Any swinging rigid body free to rotate about a fixed horizontal axis is called a compound pendulum or physical pendulum. The appropriate equivalent length $L_\text$ for calculating the period of any such pendulum is the distance from the pivot to the '' center of oscillation''., Part 4, Proposition 5 This point is located under the center of mass at a distance from the pivot traditionally called the radius of oscillation, which depends on the mass distribution of the pendulum. If most of the mass is concentrated in a relatively small bob compared to the pendulum length, the center of oscillation is close to the center of mass.

The radius of oscillation or equivalent length $L_\text$ of any physical pendulum can be shown to be
$L_\text = \frac$

where $I$ is the moment of inertia of the pendulum about the pivot point, $m$ is the mass of the pendulum, and $R$ is the distance between the pivot point and the center of mass.
Substituting this expression in (1) above, the period $T$ of a compound pendulum is given by
$T = 2\pi \sqrt\frac$
for sufficiently small oscillations.

For example, a rigid uniform rod of length $L$ pivoted about one end has moment of inertia $I = \fracmL^2$. The center of mass is located at the center of the rod, so $R = \frac L$ Substituting these values into the above equation gives $T = 2\pi\sqrt$. This shows that a rigid rod pendulum has the same period as a simple pendulum of 2/3 its length.

Christiaan Huygens proved in 1673 that the pivot point and the center of oscillation are interchangeable.Huygens (1673) Horologium Oscillatorium
Part 4, Proposition 20 This means if any pendulum is turned upside down and swung from a pivot located at its previous center of oscillation, it will have the same period as before and the new center of oscillation will be at the old pivot point. In 1817 Henry Kater used this idea to produce a type of reversible pendulum, now known as a Kater pendulum, for improved measurements of the acceleration due to gravity.

History

One of the earliest known uses of a pendulum was a 1st-century seismometer device of Han Dynasty Chinese scientist Zhang Heng.Morton, W. Scott and Charlton M. Lewis (2005). China: Its History and Culture. New York: McGraw-Hill, Inc., p. 70 Its function was to sway and activate one of a series of levers after being disturbed by the tremor of an earthquake far away.Needham, Volume 3, 627-629 Released by a lever, a small ball would fall out of the urn-shaped device into one of eight metal toad's mouths below, at the eight points of the compass, signifying the direction the earthquake was located.

Many sources claim that the 10th-century Egyptian astronomer Ibn Yunus used a pendulum for time measurement, but this was an error that originated in 1684 with the British historian Edward Bernard.

During the Renaissance, large hand-pumped pendulums were used as sources of power for manual reciprocating machines such as saws, bellows, and pumps. Leonardo da Vinci made many drawings of the motion of pendulums, though without realizing its value for timekeeping.

1602: Galileo's research

Italian scientist Galileo Galilei was the first to study the properties of pendulums, beginning around 1602. The earliest extant report of his research is contained in a letter to Guido Ubaldo dal Monte, from Padua, dated November 29, 1602. His biographer and student, Vincenzo Viviani, claimed his interest had been sparked around 1582 by the swinging motion of a chandelier in Pisa Cathedral. Galileo discovered the crucial property that makes pendulums useful as timekeepers, called isochronism; the period of the pendulum is approximately independent of the amplitude or width of the swing. He also found that the period is independent of the mass of the bob, and proportional to the square root of the length of the pendulum. He first employed freeswinging pendulums in simple timing applications. His physician friend, Santorio Santorii, invented a device which measured a patient's pulse by the length of a pendulum; the ''pulsilogium''. In 1641 Galileo dictated to his son Vincenzo a design for a pendulum clock; Vincenzo began construction, but had not completed it when he died in 1649.

1656: The pendulum clock

In 1656 the Dutch scientist Christiaan Huygens built the first pendulum clock. This was a great improvement over existing mechanical clocks; their best accuracy was improved from around 15 minutes deviation a day to around 15 seconds a day. Pendulums spread over Europe as existing clocks were retrofitted with them.

The English scientist Robert Hooke studied the conical pendulum around 1666, consisting of a pendulum that is free to swing in two dimensions, with the bob rotating in a circle or ellipse. He used the motions of this device as a model to analyze the orbital motions of the planets. Hooke suggested to Isaac Newton in 1679 that the components of orbital motion consisted of inertial motion along a tangent direction plus an attractive motion in the radial direction. This played a part in Newton's formulation of the law of universal gravitation. Robert Hooke was also responsible for suggesting as early as 1666 that the pendulum could be used to measure the force of gravity.

During his expedition to Cayenne, French Guiana in 1671, Jean Richer found that a pendulum clock was minutes per day slower at Cayenne than at Paris. From this he deduced that the force of gravity was lower at Cayenne. In 1687, Isaac Newton in '' Principia Mathematica'' showed that this was because the Earth was not a true sphere but slightly oblate (flattened at the poles) from the effect of centrifugal force due to its rotation, causing gravity to increase with latitude. Portable pendulums began to be taken on voyages to distant lands, as precision gravimeters to measure the acceleration of gravity at different points on Earth, eventually resulting in accurate models of the shape of the Earth.

1673: Huygens' ''Horologium Oscillatorium''

In 1673, 17 years after he invented the pendulum clock, Christiaan Huygens published his theory of the pendulum, '' Horologium Oscillatorium sive de motu pendulorum''. Marin Mersenne and René Descartes had discovered around 1636 that the pendulum was not quite isochronous; its period increased somewhat with its amplitude. Huygens analyzed this problem by determining what curve an object must follow to descend by gravity to the same point in the same time interval, regardless of starting point; the so-called '' tautochrone curve''. By a complicated method that was an early use of calculus, he showed this curve was a cycloid, rather than the circular arc of a pendulum, confirming that the pendulum was not isochronous and Galileo's observation of isochronism was accurate only for small swings. Huygens also solved the problem of how to calculate the period of an arbitrarily shaped pendulum (called a ''compound pendulum''), discovering the '' center of oscillation'', and its interchangeability with the pivot point.

The existing clock movement, the verge escapement, made pendulums swing in very wide arcs of about 100°. Huygens showed this was a source of inaccuracy, causing the period to vary with amplitude changes caused by small unavoidable variations in the clock's drive force. To make its period isochronous, Huygens mounted cycloidal-shaped metal guides next to the pivots in his clocks, that constrained the suspension cord and forced the pendulum to follow a cycloid arc (see cycloidal pendulum).Andrewes, W.J.H
''Clocks and Watches: The leap to precision''
in This solution didn't prove as practical as simply limiting the pendulum's swing to small angles of a few degrees. The realization that only small swings were isochronous motivated the development of the anchor escapement around 1670, which reduced the pendulum swing in clocks to 4°–6°. This became the standard escapement used in pendulum clocks.

1721: Temperature compensated pendulums

During the 18th and 19th century, the pendulum clock's role as the most accurate timekeeper motivated much practical research into improving pendulums. It was found that a major source of error was that the pendulum rod expanded and contracted with changes in ambient temperature, changing the period of swing. This was solved with the invention of temperature compensated pendulums, the mercury pendulum in 1721 cited in and the gridiron pendulum in 1726, reducing errors in precision pendulum clocks to a few seconds per week.

The accuracy of gravity measurements made with pendulums was limited by the difficulty of finding the location of their center of oscillation. Huygens had discovered in 1673 that a pendulum has the same period when hung from its center of oscillation as when hung from its pivot, and the distance between the two points was equal to the length of a simple gravity pendulum of the same period. In 1818 British Captain Henry Kater invented the reversible Kater's pendulum which used this principle, making possible very accurate measurements of gravity. For the next century the reversible pendulum was the standard method of measuring absolute gravitational acceleration.

1851: Foucault pendulum

In 1851, Jean Bernard Léon Foucault showed that the plane of oscillation of a pendulum, like a gyroscope, tends to stay constant regardless of the motion of the pivot, and that this could be used to demonstrate the rotation of the Earth. He suspended a pendulum free to swing in two dimensions (later named the Foucault pendulum) from the dome of the Panthéon in Paris. The length of the cord was . Once the pendulum was set in motion, the plane of swing was observed to precess or rotate 360° clockwise in about 32 hours.
This was the first demonstration of the Earth's rotation that didn't depend on celestial observations, and a "pendulum mania" broke out, as Foucault pendulums were displayed in many cities and attracted large crowds.

1930: Decline in use

Around 1900 low- thermal-expansion materials began to be used for pendulum rods in the highest precision clocks and other instruments, first invar, a nickel steel alloy, and later fused quartz, which made temperature compensation trivial. Precision pendulums were housed in low pressure tanks, which kept the air pressure constant to prevent changes in the period due to changes in buoyancy of the pendulum due to changing atmospheric pressure. The best pendulum clocks achieved accuracy of around a second per year.

The timekeeping accuracy of the pendulum was exceeded by the quartz crystal oscillator, invented in 1921, and quartz clocks, invented in 1927, replaced pendulum clocks as the world's best timekeepers. Pendulum clocks were used as time standards until World War 2, although the French Time Service continued using them in their official time standard ensemble until 1954. Pendulum gravimeters were superseded by "free fall" gravimeters in the 1950s, but pendulum instruments continued to be used into the 1970s.

Use for time measurement

For 300 years, from its discovery around 1582 until development of the quartz clock in the 1930s, the pendulum was the world's standard for accurate timekeeping. In addition to clock pendulums, freeswinging seconds pendulums were widely used as precision timers in scientific experiments in the 17th and 18th centuries. Pendulums require great mechanical stability: a length change of only 0.02%, 0.2 mm in a grandfather clock pendulum, will cause an error of a minute per week.

Clock pendulums

Pendulums in clocks (see example at right) are usually made of a weight or bob ''(b)'' suspended by a rod of wood or metal ''(a)''. To reduce air resistance (which accounts for most of the energy loss in precision clocks) the bob is traditionally a smooth disk with a lens-shaped cross section, although in antique clocks it often had carvings or decorations specific to the type of clock. In quality clocks the bob is made as heavy as the suspension can support and the movement can drive, since this improves the regulation of the clock (see Accuracy below). A common weight for seconds pendulum bobs is . Instead of hanging from a pivot, clock pendulums are usually supported by a short straight spring ''(d)'' of flexible metal ribbon. This avoids the friction and 'play' caused by a pivot, and the slight bending force of the spring merely adds to the pendulum's restoring force. The highest precision clocks have pivots of 'knife' blades resting on agate plates. The impulses to keep the pendulum swinging are provided by an arm hanging behind the pendulum called the ''crutch'', ''(e)'', which ends in a ''fork'', ''(f)'' whose prongs embrace the pendulum rod. The crutch is pushed back and forth by the clock's escapement, ''(g,h)''.

Each time the pendulum swings through its centre position, it releases one tooth of the ''escape wheel'' ''(g)''. The force of the clock's mainspring or a driving weight hanging from a pulley, transmitted through the clock's gear train, causes the wheel to turn, and a tooth presses against one of the pallets ''(h)'', giving the pendulum a short push. The clock's wheels, geared to the escape wheel, move forward a fixed amount with each pendulum swing, advancing the clock's hands at a steady rate.

The pendulum always has a means of adjusting the period, usually by an adjustment nut ''(c)'' under the bob which moves it up or down on the rod. Moving the bob up decreases the pendulum's length, causing the pendulum to swing faster and the clock to gain time. Some precision clocks have a small auxiliary adjustment weight on a threaded shaft on the bob, to allow finer adjustment. Some tower clocks and precision clocks use a tray attached near to the midpoint of the pendulum rod, to which small weights can be added or removed. This effectively shifts the centre of oscillation and allows the rate to be adjusted without stopping the clock.

The pendulum must be suspended from a rigid support. During operation, any elasticity will allow tiny imperceptible swaying motions of the support, which disturbs the clock's period, resulting in error. Pendulum clocks should be attached firmly to a sturdy wall.

The most common pendulum length in quality clocks, which is always used in grandfather clocks, is the seconds pendulum, about long. In mantel clocks, half-second pendulums, long, or shorter, are used. Only a few large tower clocks use longer pendulums, the 1.5 second pendulum, long, or occasionally the two-second pendulum, which is used in Big Ben.

Temperature compensation

The largest source of error in early pendulums was slight changes in length due to thermal expansion and contraction of the pendulum rod with changes in ambient temperature. This was discovered when people noticed that pendulum clocks ran slower in summer, by as much as a minute per week (one of the first was Godefroy Wendelin, as reported by Huygens in 1658). Thermal expansion of pendulum rods was first studied by Jean Picard in 1669. A pendulum with a steel rod will expand by about 11.3 parts per million (ppm) with each degree Celsius increase, causing it to lose about 0.27 seconds per day for every degree Celsius increase in temperature, or 9 seconds per day for a change. Wood rods expand less, losing only about 6 seconds per day for a change, which is why quality clocks often had wooden pendulum rods. The wood had to be varnished to prevent water vapor from getting in, because changes in humidity also affected the length.

Mercury pendulum

The first device to compensate for this error was the mercury pendulum, invented by George Graham in 1721. The liquid metal mercury expands in volume with temperature. In a mercury pendulum, the pendulum's weight (bob) is a container of mercury. With a temperature rise, the pendulum rod gets longer, but the mercury also expands and its surface level rises slightly in the container, moving its centre of mass closer to the pendulum pivot. By using the correct height of mercury in the container these two effects will cancel, leaving the pendulum's centre of mass, and its period, unchanged with temperature. Its main disadvantage was that when the temperature changed, the rod would come to the new temperature quickly but the mass of mercury might take a day or two to reach the new temperature, causing the rate to deviate during that time.Matthys 2004
p.7-12 To improve thermal accommodation several thin containers were often used, made of metal. Mercury pendulums were the standard used in precision regulator clocks into the 20th century.

Gridiron pendulum

The most widely used compensated pendulum was the gridiron pendulum, invented in 1726 by John Harrison. This consists of alternating rods of two different metals, one with lower thermal expansion ( CTE), steel, and one with higher thermal expansion, zinc or brass. The rods are connected by a frame, as shown in the drawing at the right, so that an increase in length of the zinc rods pushes the bob up, shortening the pendulum. With a temperature increase, the low expansion steel rods make the pendulum longer, while the high expansion zinc rods make it shorter. By making the rods of the correct lengths, the greater expansion of the zinc cancels out the expansion of the steel rods which have a greater combined length, and the pendulum stays the same length with temperature.

Zinc-steel gridiron pendulums are made with 5 rods, but the thermal expansion of brass is closer to steel, so brass-steel gridirons usually require 9 rods. Gridiron pendulums adjust to temperature changes faster than mercury pendulums, but scientists found that friction of the rods sliding in their holes in the frame caused gridiron pendulums to adjust in a series of tiny jumps. In high precision clocks this caused the clock's rate to change suddenly with each jump. Later it was found that zinc is subject to creep. For these reasons mercury pendulums were used in the highest precision clocks, but gridirons were used in quality regulator clocks.

Gridiron pendulums became so associated with good quality that, to this day, many ordinary clock pendulums have decorative 'fake' gridirons that don't actually have any temperature compensation function.

Invar and fused quartz

Around 1900, low thermal expansion materials were developed which could be used as pendulum rods in order to make elaborate temperature compensation unnecessary. These were only used in a few of the highest precision clocks before the pendulum became obsolete as a time standard. In 1896 Charles Édouard Guillaume invented the nickel steel alloy Invar. This has a CTE of around 0.5 µin/(in·°F), resulting in pendulum temperature errors over 71 °F of only 1.3 seconds per day, and this residual error could be compensated to zero with a few centimeters of aluminium under the pendulum bob (this can be seen in the Riefler clock image above). Invar pendulums were first used in 1898 in the Riefler regulator clock which achieved accuracy of 15 milliseconds per day. Suspension springs of Elinvar were used to eliminate temperature variation of the spring's restoring force on the pendulum. Later fused quartz was used which had even lower CTE. These materials are the choice for modern high accuracy pendulums.

Atmospheric pressure

The effect of the surrounding air on a moving pendulum is complex and requires fluid mechanics to calculate precisely, but for most purposes its influence on the period can be accounted for by three effects:
* By Archimedes' principle the effective weight of the bob is reduced by the buoyancy of the air it displaces, while the mass ( inertia) remains the same, reducing the pendulum's acceleration during its swing and increasing the period. This depends on the air pressure and the density of the pendulum, but not its shape.
* The pendulum carries an amount of air with it as it swings, and the mass of this air increases the inertia of the pendulum, again reducing the acceleration and increasing the period. This depends on both its density and shape.
* Viscous air resistance slows the pendulum's velocity. This has a negligible effect on the period, but dissipates energy, reducing the amplitude. This reduces the pendulum's Q factor, requiring a stronger drive force from the clock's mechanism to keep it moving, which causes increased disturbance to the period.
Increases in barometric pressure increase a pendulum's period slightly due to the first two effects, by about 0.11 seconds per day per kilopascal (0.37 seconds per day per inch of mercury or 0.015 seconds per day per torr). Researchers using pendulums to measure the acceleration of gravity had to correct the period for the air pressure at the altitude of measurement, computing the equivalent period of a pendulum swinging in vacuum. A pendulum clock was first operated in a constant-pressure tank by Friedrich Tiede in 1865 at the Berlin Observatory, and by 1900 the highest precision clocks were mounted in tanks that were kept at a constant pressure to eliminate changes in atmospheric pressure. Alternatively, in some a small aneroid barometer mechanism attached to the pendulum compensated for this effect.

Gravity

Pendulums are affected by changes in gravitational acceleration, which varies by as much as 0.5% at different locations on Earth, so precision pendulum clocks have to be recalibrated after a move. Even moving a pendulum clock to the top of a tall building can cause it to lose measurable time from the reduction in gravity.

Accuracy of pendulums as timekeepers

The timekeeping elements in all clocks, which include pendulums, balance wheels, the quartz crystals used in quartz watches, and even the vibrating atoms in atomic clocks, are in physics called harmonic oscillators. The reason harmonic oscillators are used in clocks is that they vibrate or oscillate at a specific resonant frequency or period and resist oscillating at other rates. However, the resonant frequency is not infinitely 'sharp'. Around the resonant frequency there is a narrow natural band of frequencies (or periods), called the resonance width or bandwidth, where the harmonic oscillator will oscillate. p.39 In a clock, the actual frequency of the pendulum may vary randomly within this resonance width in response to disturbances, but at frequencies outside this band, the clock will not function at all. The resonance width is determined by the damping, the frictional energy loss per swing of the pendulum.

''Q'' factor

The measure of a harmonic oscillator's resistance to disturbances to its oscillation period is a dimensionless parameter called the ''Q'' factor equal to the resonant frequency divided by the resonance width. The higher the ''Q'', the smaller the resonance width, and the more constant the frequency or period of the oscillator for a given disturbance. The reciprocal of the Q is roughly proportional to the limiting accuracy achievable by a harmonic oscillator as a time standard.

The ''Q'' is related to how long it takes for the oscillations of an oscillator to die out. The ''Q'' of a pendulum can be measured by counting the number of oscillations it takes for the amplitude of the pendulum's swing to decay to 1/''e'' = 36.8% of its initial swing, and multiplying by 2''π''.

In a clock, the pendulum must receive pushes from the clock's movement to keep it swinging, to replace the energy the pendulum loses to friction. These pushes, applied by a mechanism called the escapement, are the main source of disturbance to the pendulum's motion. The ''Q'' is equal to 2''π'' times the energy stored in the pendulum, divided by the energy lost to friction during each oscillation period, which is the same as the energy added by the escapement each period. It can be seen that the smaller the fraction of the pendulum's energy that is lost to friction, the less energy needs to be added, the less the disturbance from the escapement, the more 'independent' the pendulum is of the clock's mechanism, and the more constant its period is. The ''Q'' of a pendulum is given by:
$Q = \frac$
where ''M'' is the mass of the bob, is the pendulum's radian frequency of oscillation, and Γ is the frictional damping force on the pendulum per unit velocity.

''ω'' is fixed by the pendulum's period, and ''M'' is limited by the load capacity and rigidity of the suspension. So the ''Q'' of clock pendulums is increased by minimizing frictional losses (Γ). Precision pendulums are suspended on low friction pivots consisting of triangular shaped 'knife' edges resting on agate plates. Around 99% of the energy loss in a freeswinging pendulum is due to air friction, so mounting a pendulum in a vacuum tank can increase the ''Q'', and thus the accuracy, by a factor of 100.

The ''Q'' of pendulums ranges from several thousand in an ordinary clock to several hundred thousand for precision regulator pendulums swinging in vacuum. A quality home pendulum clock might have a ''Q'' of 10,000 and an accuracy of 10 seconds per month. The most accurate commercially produced pendulum clock was the Shortt-Synchronome free pendulum clock, invented in 1921. Its Invar master pendulum swinging in a vacuum tank had a ''Q'' of 110,000 and an error rate of around a second per year.

Their Q of 10³–10⁵ is one reason why pendulums are more accurate timekeepers than the balance wheels in watches, with ''Q'' around 100–300, but less accurate than the quartz crystals in quartz clocks, with ''Q'' of 10⁵–10⁶.

Escapement

Pendulums (unlike, for example, quartz crystals) have a low enough ''Q'' that the disturbance caused by the impulses to keep them moving is generally the limiting factor on their timekeeping accuracy. Therefore, the design of the escapement, the mechanism that provides these impulses, has a large effect on the accuracy of a clock pendulum. If the impulses given to the pendulum by the escapement each swing could be exactly identical, the response of the pendulum would be identical, and its period would be constant. However, this is not achievable; unavoidable random fluctuations in the force due to friction of the clock's pallets, lubrication variations, and changes in the torque provided by the clock's power source as it runs down, mean that the force of the impulse applied by the escapement varies.

If these variations in the escapement's force cause changes in the pendulum's width of swing (amplitude), this will cause corresponding slight changes in the period, since (as discussed at top) a pendulum with a finite swing is not quite isochronous. Therefore, the goal of traditional escapement design is to apply the force with the proper profile, and at the correct point in the pendulum's cycle, so force variations have no effect on the pendulum's amplitude. This is called an ''isochronous escapement''.

The Airy condition

Clockmakers had known for centuries that the disturbing effect of the escapement's drive force on the period of a pendulum is smallest if given as a short impulse as the pendulum passes through its bottom equilibrium position. If the impulse occurs before the pendulum reaches bottom, during the downward swing, it will have the effect of shortening the pendulum's natural period, so an increase in drive force will decrease the period. If the impulse occurs after the pendulum reaches bottom, during the upswing, it will lengthen the period, so an increase in drive force will increase the pendulum's period. In 1826 British astronomer George Airy proved this; specifically, he proved that if a pendulum is driven by an impulse that is symmetrical about its bottom equilibrium position, the pendulum's period will be unaffected by changes in the drive force. The most accurate escapements, such as the deadbeat, approximately satisfy this condition.

Gravity measurement

The presence of the acceleration of gravity ''g'' in the periodicity equation (1) for a pendulum means that the local gravitational acceleration of the Earth can be calculated from the period of a pendulum. A pendulum can therefore be used as a gravimeter to measure the local gravity, which varies by over 0.5% across the surface of the Earth.The value of "g" (acceleration due to gravity) at the equator is 9.780 m/s² and at the poles is 9.832 m/s², a difference of 0.53%. The pendulum in a clock is disturbed by the pushes it receives from the clock movement, so freeswinging pendulums were used, and were the standard instruments of gravimetry up to the 1930s.

The difference between clock pendulums and gravimeter pendulums is that to measure gravity, the pendulum's length as well as its period has to be measured. The period of freeswinging pendulums could be found to great precision by comparing their swing with a precision clock that had been adjusted to keep correct time by the passage of stars overhead. In the early measurements, a weight on a cord was suspended in front of the clock pendulum, and its length adjusted until the two pendulums swung in exact synchronism. Then the length of the cord was measured. From the length and the period, ''g'' could be calculated from equation (1).

The seconds pendulum

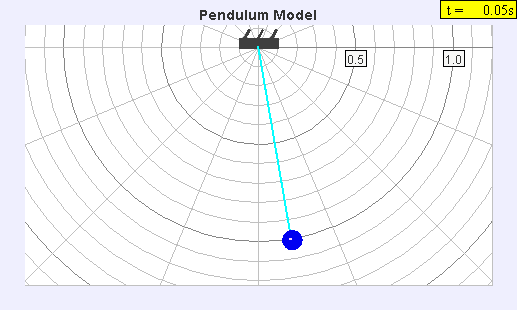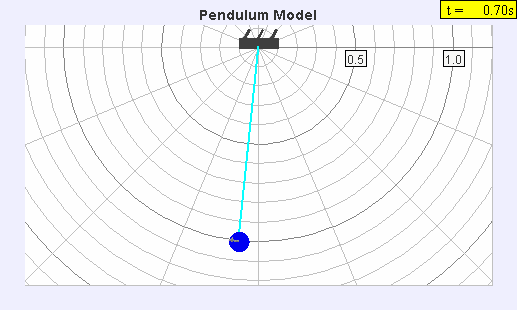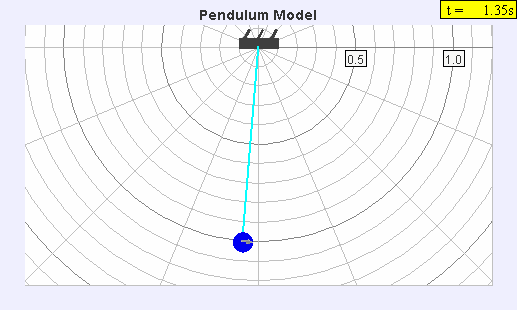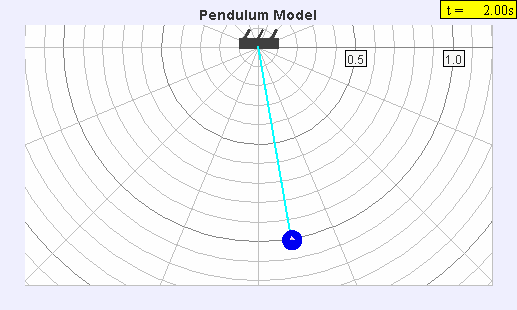
The seconds pendulum, a pendulum with a period of two seconds so each swing takes one second, was widely used to measure gravity, because its period could be easily measured by comparing it to precision regulator clocks, which all had seconds pendulums. By the late 17th century, the length of the seconds pendulum became the standard measure of the strength of gravitational acceleration at a location. By 1700 its length had been measured with submillimeter accuracy at several cities in Europe. For a seconds pendulum, ''g'' is proportional to its length:
$g \propto L.$

Early observations

* 1620: British scientist Francis Bacon was one of the first to propose using a pendulum to measure gravity, suggesting taking one up a mountain to see if gravity varies with altitude.
* 1644: Even before the pendulum clock, French priest Marin Mersenne first determined the length of the seconds pendulum was , by comparing the swing of a pendulum to the time it took a weight to fall a measured distance. He also was first to discover the dependence of the period on amplitude of swing.
* 1669: Jean Picard determined the length of the seconds pendulum at Paris, using a copper ball suspended by an aloe fiber, obtaining .Poynting & Thompson 1907, p.9
/ref> He also did the first experiments on thermal expansion and contraction of pendulum rods with temperature.
* 1672: The first observation that gravity varied at different points on Earth was made in 1672 by Jean Richer, who took a pendulum clock to Cayenne, French Guiana and found that it lost minutes per day; its seconds pendulum had to be shortened by '' lignes'' (2.6 mm) shorter than at Paris, to keep correct time. In 1687 Isaac Newton in '' Principia Mathematica'' showed this was because the Earth had a slightly oblate shape (flattened at the poles) caused by the centrifugal force of its rotation. At higher latitudes the surface was closer to the center of the Earth, so gravity increased with latitude. From this time on, pendulums began to be taken to distant lands to measure gravity, and tables were compiled of the length of the seconds pendulum at different locations on Earth. In 1743 Alexis Claude Clairaut created the first hydrostatic model of the Earth, Clairaut's theorem, which allowed the ellipticity of the Earth to be calculated from gravity measurements. Progressively more accurate models of the shape of the Earth followed.
* 1687: Newton experimented with pendulums (described in ''Principia'') and found that equal length pendulums with bobs made of different materials had the same period, proving that the gravitational force on different substances was exactly proportional to their mass (inertia). This principle, called the equivalence principle, confirmed to greater accuracy in later experiments, became the foundation on which Albert Einstein based his general theory of relativity.

* 1737: French mathematician Pierre Bouguer made a sophisticated series of pendulum observations in the Andes mountains, Peru.Poynting & Thompson, 1907, p.10
/ref> He used a copper pendulum bob in the shape of a double pointed cone suspended by a thread; the bob could be reversed to eliminate the effects of nonuniform density. He calculated the length to the center of oscillation of thread and bob combined, instead of using the center of the bob. He corrected for thermal expansion of the measuring rod and barometric pressure, giving his results for a pendulum swinging in vacuum. Bouguer swung the same pendulum at three different elevations, from sea level to the top of the high Peruvian '' altiplano''. Gravity should fall with the inverse square of the distance from the center of the Earth. Bouguer found that it fell off slower, and correctly attributed the 'extra' gravity to the gravitational field of the huge Peruvian plateau. From the density of rock samples he calculated an estimate of the effect of the ''altiplano'' on the pendulum, and comparing this with the gravity of the Earth was able to make the first rough estimate of the density of the Earth.
* 1747: Daniel Bernoulli showed how to correct for the lengthening of the period due to a finite angle of swing ''θ''₀ by using the first order correction ''θ''₀²/16, giving the period of a pendulum with an extremely small swing.
* 1792: To define a pendulum standard of length for use with the new metric system, in 1792 Jean-Charles de Borda and Jean-Dominique Cassini made a precise measurement of the seconds pendulum at Paris. They used a -inch (14 mm) platinum ball suspended by a iron wire. Their main innovation was a technique called the "''method of coincidences''" which allowed the period of pendulums to be compared with great precision. (Bouguer had also used this method). The time interval Δ''t'' between the recurring instants when the two pendulums swung in synchronism was timed. From this the difference between the periods of the pendulums, ''T''₁ and ''T''₂, could be calculated: $\frac = \frac - \frac$
* 1821: Francesco Carlini made pendulum observations on top of Mount Cenis, Italy, from which, using methods similar to Bouguer's, he calculated the density of the Earth. He compared his measurements to an estimate of the gravity at his location assuming the mountain wasn't there, calculated from previous nearby pendulum measurements at sea level. His measurements showed 'excess' gravity, which he allocated to the effect of the mountain. Modeling the mountain as a segment of a sphere in diameter and high, from rock samples he calculated its gravitational field, and estimated the density of the Earth at 4.39 times that of water. Later recalculations by others gave values of 4.77 and 4.95, illustrating the uncertainties in these geographical methods.

Kater's pendulum

The precision of the early gravity measurements above was limited by the difficulty of measuring the length of the pendulum, ''L'' . ''L'' was the length of an idealized simple gravity pendulum (described at top), which has all its mass concentrated in a point at the end of the cord. In 1673 Huygens had shown that the period of a rigid bar pendulum (called a ''compound pendulum'') was equal to the period of a simple pendulum with a length equal to the distance between the pivot point and a point called the center of oscillation, located under the center of gravity, that depends on the mass distribution along the pendulum. But there was no accurate way of determining the center of oscillation in a real pendulum.

To get around this problem, the early researchers above approximated an ideal simple pendulum as closely as possible by using a metal sphere suspended by a light wire or cord. If the wire was light enough, the center of oscillation was close to the center of gravity of the ball, at its geometric center. This "ball and wire" type of pendulum wasn't very accurate, because it didn't swing as a rigid body, and the elasticity of the wire caused its length to change slightly as the pendulum swung.

However Huygens had also proved that in any pendulum, the pivot point and the center of oscillation were interchangeable. That is, if a pendulum were turned upside down and hung from its center of oscillation, it would have the same period as it did in the previous position, and the old pivot point would be the new center of oscillation.

British physicist and army captain Henry Kater in 1817 realized that Huygens' principle could be used to find the length of a simple pendulum with the same period as a real pendulum. If a pendulum was built with a second adjustable pivot point near the bottom so it could be hung upside down, and the second pivot was adjusted until the periods when hung from both pivots were the same, the second pivot would be at the center of oscillation, and the distance between the two pivots would be the length ''L'' of a simple pendulum with the same period.

Kater built a reversible pendulum (shown at right) consisting of a brass bar with two opposing pivots made of short triangular "knife" blades ''(a)'' near either end. It could be swung from either pivot, with the knife blades supported on agate plates. Rather than make one pivot adjustable, he attached the pivots a meter apart and instead adjusted the periods with a moveable weight on the pendulum rod ''(b,c)''. In operation, the pendulum is hung in front of a precision clock, and the period timed, then turned upside down and the period timed again. The weight is adjusted with the adjustment screw until the periods are equal. Then putting this period and the distance between the pivots into equation (1) gives the gravitational acceleration ''g'' very accurately.

Kater timed the swing of his pendulum using the "''method of coincidences''" and measured the distance between the two pivots with a micrometer. After applying corrections for the finite amplitude of swing, the buoyancy of the bob, the barometric pressure and altitude, and temperature, he obtained a value of 39.13929 inches for the seconds pendulum at London, in vacuum, at sea level, at 62 °F. The largest variation from the mean of his 12 observations was 0.00028 in. representing a precision of gravity measurement of 7×10⁻⁶ (7 mGal or 70 µm/s²). Kater's measurement was used as Britain's official standard of length (see below) from 1824 to 1855.

Reversible pendulums (known technically as "convertible" pendulums) employing Kater's principle were used for absolute gravity measurements into the 1930s.

Later pendulum gravimeters

The increased accuracy made possible by Kater's pendulum helped make gravimetry a standard part of geodesy. Since the exact location (latitude and longitude) of the 'station' where the gravity measurement was made was necessary, gravity measurements became part of surveying, and pendulums were taken on the great geodetic surveys of the 18th century, particularly the Great Trigonometric Survey of India.

* Invariable pendulums: Kater introduced the idea of ''relative'' gravity measurements, to supplement the ''absolute'' measurements made by a Kater's pendulum. Comparing the gravity at two different points was an easier process than measuring it absolutely by the Kater method. All that was necessary was to time the period of an ordinary (single pivot) pendulum at the first point, then transport the pendulum to the other point and time its period there. Since the pendulum's length was constant, from (1) the ratio of the gravitational accelerations was equal to the inverse of the ratio of the periods squared, and no precision length measurements were necessary. So once the gravity had been measured absolutely at some central station, by the Kater or other accurate method, the gravity at other points could be found by swinging pendulums at the central station and then taking them to the other location and timing their swing there. Kater made up a set of "invariable" pendulums, with only one knife edge pivot, which were taken to many countries after first being swung at a central station at Kew Observatory, UK.
* Airy's coal pit experiments: Starting in 1826, using methods similar to Bouguer, British astronomer George Airy attempted to determine the density of the Earth by pendulum gravity measurements at the top and bottom of a coal mine. The gravitational force below the surface of the Earth decreases rather than increasing with depth, because by Gauss's law the mass of the spherical shell of crust above the subsurface point does not contribute to the gravity. The 1826 experiment was aborted by the flooding of the mine, but in 1854 he conducted an improved experiment at the Harton coal mine, using seconds pendulums swinging on agate plates, timed by precision chronometers synchronized by an electrical circuit. He found the lower pendulum was slower by 2.24 seconds per day. This meant that the gravitational acceleration at the bottom of the mine, 1250 ft below the surface, was 1/14,000 less than it should have been from the inverse square law; that is the attraction of the spherical shell was 1/14,000 of the attraction of the Earth. From samples of surface rock he estimated the mass of the spherical shell of crust, and from this estimated that the density of the Earth was 6.565 times that of water. Von Sterneck attempted to repeat the experiment in 1882 but found inconsistent results.

* Repsold-Bessel pendulum: It was time-consuming and error-prone to repeatedly swing the Kater's pendulum and adjust the weights until the periods were equal. Friedrich Bessel showed in 1835 that this was unnecessary. As long as the periods were close together, the gravity could be calculated from the two periods and the center of gravity of the pendulum. So the reversible pendulum didn't need to be adjustable, it could just be a bar with two pivots. Bessel also showed that if the pendulum was made symmetrical in form about its center, but was weighted internally at one end, the errors due to air drag would cancel out. Further, another error due to the finite diameter of the knife edges could be made to cancel out if they were interchanged between measurements. Bessel didn't construct such a pendulum, but in 1864 Adolf Repsold, under contract by the Swiss Geodetic Commission made a pendulum along these lines. The Repsold pendulum was about 56 cm long and had a period of about second. It was used extensively by European geodetic agencies, and with the Kater pendulum in the Survey of India. Similar pendulums of this type were designed by Charles Pierce and C. Defforges.

* Von Sterneck and Mendenhall gravimeters: In 1887 Austro-Hungarian scientist Robert von Sterneck developed a small gravimeter pendulum mounted in a temperature-controlled vacuum tank to eliminate the effects of temperature and air pressure. It used a "half-second pendulum," having a period close to one second, about 25 cm long. The pendulum was nonreversible, so the instrument was used for relative gravity measurements, but their small size made them small and portable. The period of the pendulum was picked off by reflecting the image of an electric spark created by a precision chronometer off a mirror mounted at the top of the pendulum rod. The Von Sterneck instrument, and a similar instrument developed by Thomas C. Mendenhall of the United States Coast and Geodetic Survey in 1890, were used extensively for surveys into the 1920s.

:The Mendenhall pendulum was actually a more accurate timekeeper than the highest precision clocks of the time, and as the 'world's best clock' it was used by Albert A. Michelson in his 1924 measurements of the speed of light on Mt. Wilson, California.
* Double pendulum gravimeters: Starting in 1875, the increasing accuracy of pendulum measurements revealed another source of error in existing instruments: the swing of the pendulum caused a slight swaying of the tripod stand used to support portable pendulums, introducing error. In 1875 Charles S Peirce calculated that measurements of the length of the seconds pendulum made with the Repsold instrument required a correction of 0.2 mm due to this error. In 1880 C. Defforges used a Michelson interferometer to measure the sway of the stand dynamically, and interferometers were added to the standard Mendenhall apparatus to calculate sway corrections. A method of preventing this error was first suggested in 1877 by Hervé Faye and advocated by Peirce, Cellérier and Furtwangler: mount two identical pendulums on the same support, swinging with the same amplitude, 180° out of phase. The opposite motion of the pendulums would cancel out any sideways forces on the support. The idea was opposed due to its complexity, but by the start of the 20th century the Von Sterneck device and other instruments were modified to swing multiple pendulums simultaneously.

* Gulf gravimeter: One of the last and most accurate pendulum gravimeters was the apparatus developed in 1929 by the Gulf Research and Development Co. It used two pendulums made of fused quartz, each in length with a period of 0.89 second, swinging on pyrex knife edge pivots, 180° out of phase. They were mounted in a permanently sealed temperature and humidity controlled vacuum chamber. Stray electrostatic charges on the quartz pendulums had to be discharged by exposing them to a radioactive salt before use. The period was detected by reflecting a light beam from a mirror at the top of the pendulum, recorded by a chart recorder and compared to a precision crystal oscillator calibrated against the WWV radio time signal. This instrument was accurate to within (0.3–0.5)×10⁻⁷ (30–50 microgals or 3–5 nm/s²). It was used into the 1960s.

Relative pendulum gravimeters were superseded by the simpler LaCoste zero-length spring gravimeter, invented in 1934 by Lucien LaCoste. Absolute (reversible) pendulum gravimeters were replaced in the 1950s by free fall gravimeters, in which a weight is allowed to fall in a vacuum tank and its acceleration is measured by an optical interferometer.

Standard of length

Because the acceleration of gravity is constant at a given point on Earth, the period of a simple pendulum at a given location depends only on its length. Additionally, gravity varies only slightly at different locations. Almost from the pendulum's discovery until the early 19th century, this property led scientists to suggest using a pendulum of a given period as a standard of length.

Until the 19th century, countries based their systems of length measurement on prototypes, metal bar primary standards, such as the standard yard in Britain kept at the Houses of Parliament, and the standard '' toise'' in France, kept at Paris. These were vulnerable to damage or destruction over the years, and because of the difficulty of comparing prototypes, the same unit often had different lengths in distant towns, creating opportunities for fraud. During the Enlightenment scientists argued for a length standard that was based on some property of nature that could be determined by measurement, creating an indestructible, universal standard. The period of pendulums could be measured very precisely by timing them with clocks that were set by the stars. A pendulum standard amounted to defining the unit of length by the gravitational force of the Earth, for all intents constant, and the second, which was defined by the rotation rate of the Earth, also constant. The idea was that anyone, anywhere on Earth, could recreate the standard by constructing a pendulum that swung with the defined period and measuring its length.

Virtually all proposals were based on the seconds pendulum, in which each swing (a half period) takes one second, which is about a meter (39 inches) long, because by the late 17th century it had become a standard for measuring gravity (see previous section). By the 18th century its length had been measured with sub-millimeter accuracy at a number of cities in Europe and around the world.

The initial attraction of the pendulum length standard was that it was believed (by early scientists such as Huygens and Wren) that gravity was constant over the Earth's surface, so a given pendulum had the same period at any point on Earth. So the length of the standard pendulum could be measured at any location, and would not be tied to any given nation or region; it would be a truly democratic, worldwide standard. Although Richer found in 1672 that gravity varies at different points on the globe, the idea of a pendulum length standard remained popular, because it was found that gravity only varies with latitude. Gravitational acceleration increases smoothly from the equator to the poles, due to the oblate shape of the Earth, so at any given latitude (east–west line), gravity was constant enough that the length of a seconds pendulum was the same within the measurement capability of the 18th century. Thus the unit of length could be defined at a given latitude and measured at any point along that latitude. For example, a pendulum standard defined at 45° north latitude, a popular choice, could be measured in parts of France, Italy, Croatia, Serbia, Romania, Russia, Kazakhstan, China, Mongolia, the United States and Canada. In addition, it could be recreated at any location at which the gravitational acceleration had been accurately measured.

By the mid 19th century, increasingly accurate pendulum measurements by Edward Sabine and Thomas Young revealed that gravity, and thus the length of any pendulum standard, varied measurably with local geologic features such as mountains and dense subsurface rocks. So a pendulum length standard had to be defined at a single point on Earth and could only be measured there. This took much of the appeal from the concept, and efforts to adopt pendulum standards were abandoned.

Early proposals

One of the first to suggest defining length with a pendulum was Flemish scientist Isaac Beeckman who in 1631 recommended making the seconds pendulum "the invariable measure for all people at all times in all places". Marin Mersenne, who first measured the seconds pendulum in 1644, also suggested it. The first official proposal for a pendulum standard was made by the British Royal Society in 1660, advocated by Christiaan Huygens and Ole Rømer, basing it on Mersenne's work, and Huygens in '' Horologium Oscillatorium'' proposed a "horary foot" defined as 1/3 of the seconds pendulum. Christopher Wren was another early supporter. The idea of a pendulum standard of length must have been familiar to people as early as 1663, because Samuel Butler satirizes it in '' Hudibras'':
:Upon the bench I will so handle ‘em
:That the vibration of this pendulum
:Shall make all taylors’ yards of one
:Unanimous opinion
In 1671 Jean Picard proposed a pendulum-defined 'universal foot' in his influential ''Mesure de la Terre''. Gabriel Mouton around 1670 suggested defining the '' toise'' either by a seconds pendulum or a minute of terrestrial degree. A plan for a complete system of units based on the pendulum was advanced in 1675 by Italian polymath Tito Livio Burratini. In France in 1747, geographer Charles Marie de la Condamine proposed defining length by a seconds pendulum at the equator; since at this location a pendulum's swing wouldn't be distorted by the Earth's rotation. James Steuart (1780) and George Skene Keith were also supporters.

By the end of the 18th century, when many nations were reforming their weight and measure systems, the seconds pendulum was the leading choice for a new definition of length, advocated by prominent scientists in several major nations. In 1790, then US Secretary of State Thomas Jefferson proposed to Congress a comprehensive decimalized US 'metric system' based on the seconds pendulum at 38° North latitude, the mean latitude of the United States. No action was taken on this proposal. In Britain the leading advocate of the pendulum was politician John Riggs Miller. When his efforts to promote a joint British–French–American metric system fell through in 1790, he proposed a British system based on the length of the seconds pendulum at London. This standard was adopted in 1824 (below).

The metre

In the discussions leading up to the French adoption of the metric system in 1791, the leading candidate for the definition of the new unit of length, the metre, was the seconds pendulum at 45° North latitude. It was advocated by a group led by French politician Talleyrand and mathematician Antoine Nicolas Caritat de Condorcet. This was one of the three final options considered by the French Academy of Sciences committee. However, on March 19, 1791, the committee instead chose to base the metre on the length of the meridian through Paris. A pendulum definition was rejected because of its variability at different locations, and because it defined length by a unit of time. (However, since 1983 the metre has been officially defined in terms of the length of the second and the speed of light.) A possible additional reason is that the radical French Academy didn't want to base their new system on the second, a traditional and nondecimal unit from the ''ancien regime''.

Although not defined by the pendulum, the final length chosen for the metre, 10⁻⁷ of the pole-to-equator meridian arc, was very close to the length of the seconds pendulum (0.9937 m), within 0.63%. Although no reason for this particular choice was given at the time, it was probably to facilitate the use of the seconds pendulum as a secondary standard, as was proposed in the official document. So the modern world's standard unit of length is certainly closely linked historically with the seconds pendulum.

Britain and Denmark

Britain and Denmark appear to be the only nations that (for a short time) based their units of length on the pendulum. In 1821 the Danish inch was defined as 1/38 of the length of the mean solar seconds pendulum at 45° latitude at the meridian of Skagen, at sea level, in vacuum. The British parliament passed the ''Imperial Weights and Measures Act'' in 1824, a reform of the British standard system which declared that if the prototype standard yard was destroyed, it would be recovered by defining the inch so that the length of the solar seconds pendulum at London, at sea level, in a vacuum, at 62 °F was 39.1393 inches. This also became the US standard, since at the time the US used British measures. However, when the prototype yard was lost in the 1834 Houses of Parliament fire, it proved impossible to recreate it accurately from the pendulum definition, and in 1855 Britain repealed the pendulum standard and returned to prototype standards.

Other uses

Seismometers

A pendulum in which the rod is not vertical but almost horizontal was used in early seismometers for measuring Earth tremors. The bob of the pendulum does not move when its mounting does, and the difference in the movements is recorded on a drum chart.

Schuler tuning

As first explained by Maximilian Schuler in a 1923 paper, a pendulum whose period exactly equals the orbital period of a hypothetical satellite orbiting just above the surface of the Earth (about 84 minutes) will tend to remain pointing at the center of the Earth when its support is suddenly displaced. This principle, called Schuler tuning, is used in inertial guidance systems in ships and aircraft that operate on the surface of the Earth. No physical pendulum is used, but the control system that keeps the inertial platform containing the gyroscopes stable is modified so the device acts as though it is attached to such a pendulum, keeping the platform always facing down as the vehicle moves on the curved surface of the Earth.

Coupled pendulums

In 1665 Huygens made a curious observation about pendulum clocks. Two clocks had been placed on his mantlepiece, and he noted that they had acquired an opposing motion. That is, their pendulums were beating in unison but in the opposite direction; 180° out of phase. Regardless of how the two clocks were started, he found that they would eventually return to this state, thus making the first recorded observation of a coupled oscillator.

The cause of this behavior was that the two pendulums were affecting each other through slight motions of the supporting mantlepiece. This process is called entrainment or mode locking in physics and is observed in other coupled oscillators. Synchronized pendulums have been used in clocks and were widely used in gravimeters in the early 20th century. Although Huygens only observed out-of-phase synchronization, recent investigations have shown the existence of in-phase synchronization, as well as "death" states wherein one or both clocks stops.

Religious practice

Pendulum motion appears in religious ceremonies as well. The swinging incense burner called a censer, also known as a thurible, is an example of a pendulum. Pendulums are also seen at many gatherings in eastern Mexico where they mark the turning of the tides on the day which the tides are at their highest point. See also pendulums for divination and dowsing.

Education

Pendulums are widely used in science education as an example of a harmonic oscillator, to teach dynamics and oscillatory motion. One use is to demonstrate the law of conservation of energy. A heavy object such as a bowling ball or wrecking ball is attached to a string. The weight is then moved to within a few inches of a volunteer's face, then released and allowed to swing and come back. In most instances, the weight reverses direction and then returns to (almost) the same position as the original release location — ''i.e.'' a small distance from the volunteer's face — thus leaving the volunteer unharmed. On occasion the volunteer is injured if either the volunteer does not stand still or the pendulum is initially released with a push (so that when it returns it surpasses the release position).

Torture device

It is claimed that the pendulum was used as an instrument of torture and execution by the Spanish Inquisition in the 18th century. The allegation is contained in the 1826 book ''The history of the Inquisition of Spain '' by the Spanish priest, historian and liberal activist Juan Antonio Llorente. A swinging pendulum whose edge is a knife blade slowly descends toward a bound prisoner until it cuts into his body. This method of torture came to popular consciousness through the 1842 short story " The Pit and the Pendulum" by American author Edgar Allan Poe but there is considerable skepticism that it actually was used.

Most knowledgeable sources are skeptical that this torture was ever actually used. The only evidence of its use is one paragraph in the preface to Llorente's 1826 ''History'', relating a second-hand account by a single prisoner released from the Inquisition's Madrid dungeon in 1820, who purportedly described the pendulum torture method. Modern sources point out that due to Jesus' admonition against bloodshed, Inquisitors were only allowed to use torture methods which did not spill blood, and the pendulum method would have violated this stricture. One theory is that Llorente misunderstood the account he heard; the prisoner was actually referring to another common Inquisition torture, the ''strappado'' (garrucha), in which the prisoner has his hands tied behind his back and is hoisted off the floor by a rope tied to his hands. This method was also known as the "pendulum". Poe's popular horror tale, and public awareness of the Inquisition's other brutal methods, has kept the myth of this elaborate torture method alive.

See also

Notes

The value of g reflected by the period of a pendulum varies from place to place. The gravitational force varies with distance from the center of the Earth, i.e. with altitude - or because the Earth's shape is oblate, g varies with latitude.
A more important cause of this reduction in g at the equator is because the equator is spinning at one revolution per day, so the acceleration by the gravitational force is partially canceled there by the centrifugal force.

References

Further reading

* G. L. Baker and J. A. Blackburn (2009). ''The Pendulum: A Case Study in Physics'' (Oxford University Press).
* M. Gitterman (2010). ''The Chaotic Pendulum'' (World Scientific).
* Michael R. Matthews, Arthur Stinner, Colin F. Gauld (2005) ''The Pendulum: Scientific, Historical, Philosophical and Educational Perspectives'', Springer
*
* Schlomo Silbermann,(2014) "Pendulum Fundamental; The Path Of Nowhere" (Book)
*
*
* L. P. Pook (2011). ''Understanding Pendulums: A Brief Introduction'' (Springer).

External links

{{Authority control