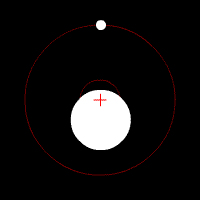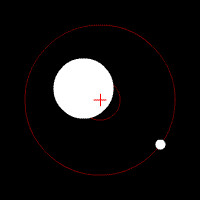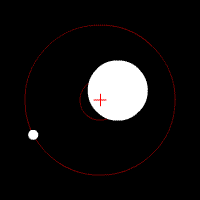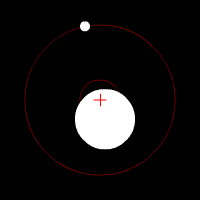
|
Pendulum Phase Portrait
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing. From the first scientific investigations of the pendulum around 1602 by Galileo Galilei, the regular motion of pendulums was used for timekeeping and was the world's most accurate timekeeping technology until the 1930s. The pendulum clock invented by Christiaan Huygens in 1658 became the world's standard timekeeper, used in homes and offices for 270 years, and a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Gravity Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing. From the first scientific investigations of the pendulum around 1602 by Galileo Galilei, the regular motion of pendulums was used for timekeeping and was the world's most accurate timekeeping technology until the 1930s. The pendulum clock invented by Christiaan Huygens in 1658 became the world's standard timekeeper, used in homes and offices for 270 years, and a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New Latin
New Latin (also called Neo-Latin or Modern Latin) is the revival of Literary Latin used in original, scholarly, and scientific works since about 1500. Modern scholarly and technical nomenclature, such as in zoological and botanical taxonomy and international scientific vocabulary, draws extensively from New Latin vocabulary, often in the form of classical or neoclassical compounds. New Latin includes extensive new word formation. As a language for full expression in prose or poetry, however, it is often distinguished from its successor, Contemporary Latin. Extent Classicists use the term "Neo-Latin" to describe the Latin that developed in Renaissance Italy as a result of renewed interest in classical civilization in the 14th and 15th centuries. Neo-Latin also describes the use of the Latin language for any purpose, scientific or literary, during and after the Renaissance. The beginning of the period cannot be precisely identified; however, the spread of secular education, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grandfather Clock
A grandfather clock (also a longcase clock, tall-case clock, grandfather's clock, or floor clock) is a tall, freestanding, weight-driven pendulum clock with the pendulum held inside the tower or waist of the case. Clocks of this style are commonly 1.8–2.4 metres (6–8 feet) tall with an enclosed pendulum and weights suspended by either cables or chains which have to be calibrated occasionally to keep the proper time. The case often features elaborately carved ornamentation on the hood (or bonnet), which surrounds and frames the dial, or clock face. The English clockmaker William Clement is credited with the development of this form in 1670. Until the early 20th century, pendulum clocks were the world's most accurate timekeeping technology, and longcase clocks, due to their superior accuracy, served as time standards for households and businesses. Today they are kept mainly for their decorative and antique value, having been widely replaced by both analog and digital ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Series
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 17th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginning of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is zero. In addition to defining mechanical equilibrium in terms of force, there are many alternative definitions for mechanical equilibrium which are all mathematically equivalent. In terms of momentum, a system is in equilibrium if the momentum of its parts is all constant. In terms of velocity, the system is in equilibrium if velocity is constant. In a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero. More generally in conservative systems, equilibrium is established at a point in configuration space where the gradient of the potential energy with respect to the generalized coordinates is zero. If a particle in equilibrium has zero velocity, that particle is in static equilibrium. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isochronism
A sequence of events is isochronous if the events occur regularly, or at equal time intervals. The term ''isochronous'' is used in several technical contexts, but usually refers to the primary subject maintaining a constant period or interval (the reciprocal of frequency), despite variations in other measurable factors in the same system. Isochronous timing is a characteristic of a repeating event whereas synchronous timing refers to the relationship between two or more events. *In dynamical systems theory, an oscillator is called ''isochronous'' if its frequency is independent of its amplitude. *In horology, a mechanical clock or watch is ''isochronous'' if it runs at the same rate regardless of changes in its drive force, so that it keeps correct time as its mainspring unwinds or chain length varies. Isochrony is important in timekeeping devices. Simply put, if a power providing device (ie a spring or weight) provides constant torque to the wheel train, it is isochronous (sinc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. Angles formed by two rays lie in the plane (geometry), plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection. ''Angle'' is also used to designate the measurement, measure of an angle or of a Rotation (mathematics), rotation. This measure is the ratio of the length of a arc (geometry), circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag). This is the steady gain in speed caused exclusively by the force of gravitational attraction. All bodies accelerate in vacuum at the same rate, regardless of the masses or compositions of the bodies; the measurement and analysis of these rates is known as gravimetry. At a fixed point on the surface, the magnitude of Earth's gravity results from combined effect of gravitation and the centrifugal force from Earth's rotation. At different points on Earth's surface, the free fall acceleration ranges from , depending on altitude, latitude, and longitude. A conventional standard value is defined exactly as . Locations of significant variation from this value are known as gravity anomalies. This does not take into account other effects, such as buoyancy or drag. Relation to the Universal Law Newton's law of universal gravitation states that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Length
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the International System of Units (SI) system the base unit for length is the metre. Length is commonly understood to mean the most extended dimension of a fixed object. However, this is not always the case and may depend on the position the object is in. Various terms for the length of a fixed object are used, and these include height, which is vertical length or vertical extent, and width, breadth or depth. Height is used when there is a base from which vertical measurements can be taken. Width or breadth usually refer to a shorter dimension when length is the longest one. Depth is used for the third dimension of a three dimensional object. Length is the measure of one spatial dimension, whereas area is a measure of two dimensions (length square ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pendulum (mathematics)
A pendulum is a body suspended from a fixed support so that it swings freely back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations. Simple gravity pendulum A ''simple gravity pendulum'' is an idealized mathematical model of a real pendulum. This is a weight (or bob) on the end of a massless cord suspended from a pivot, without friction. Since in this model there is no frictional energy loss, when given an initial displacement it wil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equations Of Motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time.''Encyclopaedia of Physics'' (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3 More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system.''Analytical Mechanics'', L.N. Hand, J.D. Finch, Cambridge University Press, 2008, The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
