Particle in a spherically symmetric potential

In quantum mechanics, a spherically symmetric potential is a system of which the potential only depends on the radial distance from the spherical center and a location in space. A particle in a spherically symmetric potential will behave accordingly to said potential and can therefore be used as an approximation, for example, of the electron in a hydrogen atom or of the formation of chemical bonds.

In the general time-independent case, the dynamics of a particle in a spherically symmetric potential are governed by a Hamiltonian of the following form:$\hat = \frac + V()$
Here, $m_0$ is the mass of the particle, $\hat$ is the momentum operator, and the potential $V(r)$ depends only on the vector magnitude of the position vector, that is, the radial distance from the origin (hence the spherical symmetry of the problem).

To describe a particle in a spherically symmetric system, it is convenient to use spherical coordinates; denoted by $r$, $\theta$ and $\phi$. The time-independent Schrödinger equation for the system is then a separable, partial differential equation. This means solutions to the angular dimensions of the equation can be found independently of the radial dimension. This leaves an ordinary differential equation in terms only of the radius, $r$, which determines the eigenstates for the particular potential, $V(r)$.

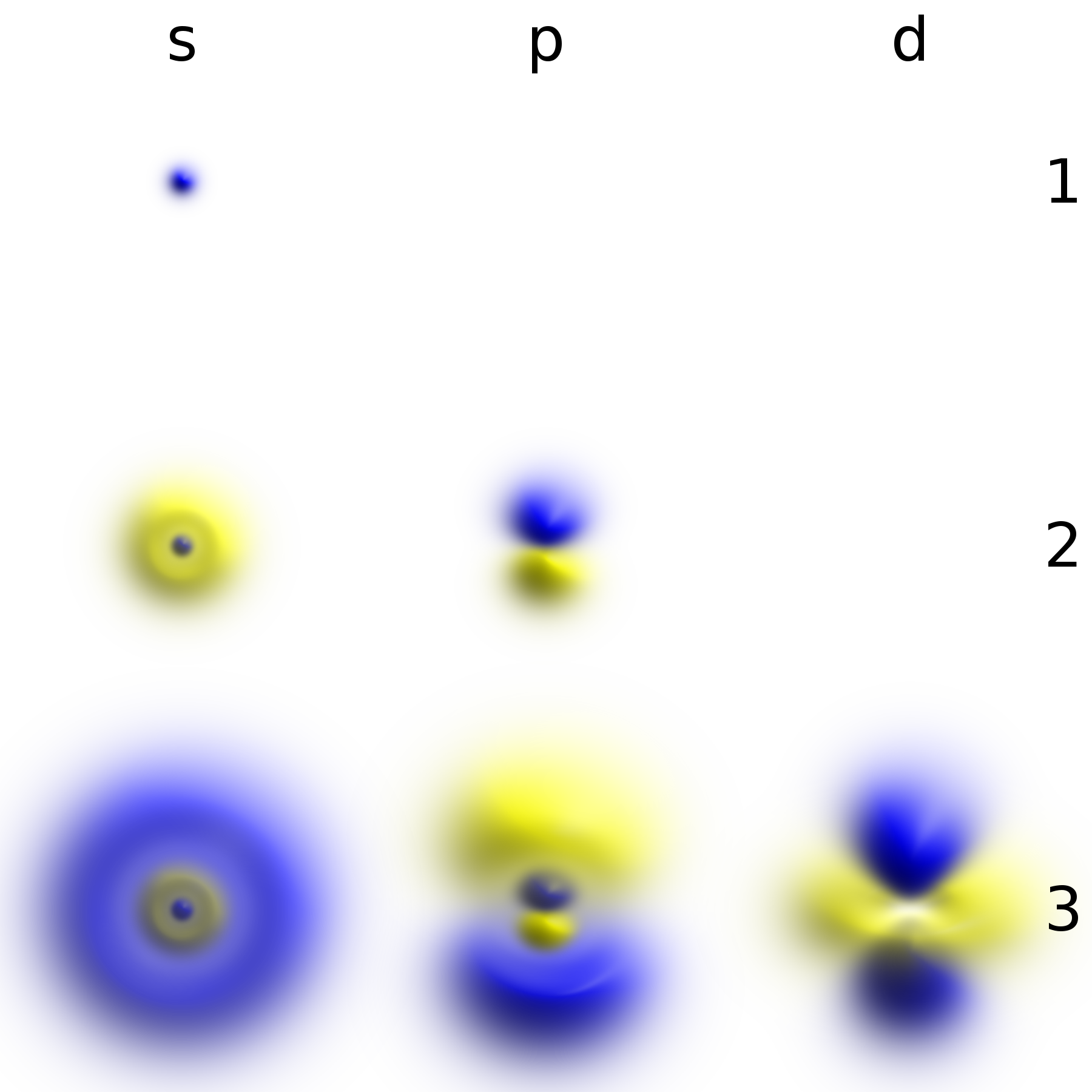
Structure of the eigenfunctions

If solved by separation of variables, the eigenstates of the system will have the form:$\psi(r, \theta, \phi) = R(r)\Theta(\theta)\Phi(\phi)$
in which the spherical angles $\theta$ and $\phi$ represent the polar and azimuthal angle, respectively. Those two factors of $\psi$ are often grouped together as spherical harmonics, so that the eigenfunctions take the form:
$\psi(r, \theta, \phi) = R(r)Y_(\theta,\phi).$

The differential equation which characterises the function $R(r)$ is called the radial equation.

Derivation of the radial equation

The kinetic energy operator in spherical polar coordinates is:\frac = -\frac \nabla^2 =
- \frac \left \frac \left(r^2 \frac\right) - \hat^2 \rightThe spherical harmonics satisfy$\hat^2 Y_(\theta,\phi)\equiv \left\ Y_(\theta,\phi) = \ell(\ell+1)Y_(\theta,\phi).$
Substituting this into the Schrödinger equation we get a one-dimensional eigenvalue equation, \frac\frac \left(r^2\frac\right) - \frac R + \frac \left -V(r)\right = 0.This equation can be reduced to an equivalent 1-D Schrödinger equation by substituting $R(r) = u(r)/r$, where $u(r)$ satisfies + \frac \left -V_(r)\rightu = 0which is precisely the one-dimensional Schrödinger equation with an effective potential given by$V_(r) = V(r) + ,$where $r \in [0,\infty)$. The correction to the potential ''V''(''r'') is called the centrifugal barrier term.

If $\lim_ r^2 V(r) =0$, then near the origin, $R \sim r^\ell$.

Spherically symmetric Hamiltonians

Since the Hamiltonian is spherically symmetric, it is said to be invariant under rotation, ie:

$^\dagger \hat U(R)=\hat$

Since angular momentum operators are generators of rotation, applying the Baker–Campbell–Hausdorff formula, Baker-Campbell-Hausdorff Lemma we get:

^\dagger \hat U(R) = e^ \hat e^ =\hat + i\frac\left[ \hat\cdot \vec, \hat\right] +\frac 1 \left( i\frac\right)^2\left \hat\cdot \vec,\left[ \hat\cdot \vec, \hat\rightright">\hat\cdot_\vec,_\hat\right.html" ;"title="\hat\cdot \vec,\left[ \hat\cdot \vec, \hat\right">\hat\cdot \vec,\left[ \hat\cdot \vec, \hat\rightright + \cdots = \hat H

Since this equation holds for all values of $\theta$, we get that $[ \hat\cdot \vec, \hat] =0$, or that every angular momentum component commutes with the Hamiltonian.

Since $L_z$ and $L^2$ are such mutually commuting operators that also commute with the Hamiltonian, the wavefunctions can be expressed as $, \alpha;\ell,m\rangle$ or $\psi_(r,\theta,\phi)$ where $\alpha$ is used to label different wavefunctions.

Since $L_\pm = L_x \pm i L_y$ also commutes with the Hamiltonian, the energy eigenvalues in such cases are always independent of $m$.

$\hat H , \alpha; \ell,m\rangle = E_, \alpha; \ell,m\rangle$

Combined with the fact that $L_\pm$ differential operators only act on the functions of $\theta$ and $\phi$, it shows that if the solutions are assumed to be separable as $\psi(r, \theta, \phi) = R(r) Y(\theta,\phi)$, the radial wavefunction $R(r)$ can always be chosen independent of $m$ values. Thus the wavefunction is expressed as:

$\psi_(r, \theta, \phi) = R(r)_Y_(\theta,\phi).$

Solutions for potentials of interest

There are five cases of special importance:
#$V(r) = 0$, or solving the vacuum in the basis of spherical harmonics, which serves as the basis for other cases.
#$V(r)=V_0$ (finite) for r and zero elsewhere.
# $V(r) = 0$ for $r < r_0$ and infinite elsewhere, the spherical equivalent of the square well, useful to describe bound states in a nucleus or quantum dot.
#$V(r) \propto r^$for the three-dimensional isotropic harmonic oscillator.
#$V(r) \propto \frac$ to describe bound states of hydrogen-like atoms.

The solutions are outlined in these cases, which should be compared to their counterparts in cartesian coordinates, cf. particle in a box.

Vacuum case states

Let us now consider $V(r) = 0$. Introducing the dimensionless variables$\rho\ \stackrel\ kr, \qquad k\ \stackrel\ \sqrt,$the equation becomes a Bessel equation for $J(\rho)\ \stackrel\ \sqrt\rho R(r)$:\rho^2\frac+\rho \frac+\left rho^2-\left(\ell+\frac\right)^2 \rightJ = 0where regular solutions for positive energies are given by so-called ''Bessel functions of the first kind'' $J_(\rho)$ so that the solutions written for $R(r)$ are the so-called ''spherical Bessel function''

$R(r) = j_l(kr) \ \stackrel\ \sqrt J_(kr)$.

The solutions of the Schrödinger equation in polar coordinates in vacuum are thus labelled by three quantum numbers: discrete indices ''ℓ'' and ''m'', and ''k'' varying continuously in $$\psi(\mathbf) = j_\ell(kr) Y_(\theta,\phi)These solutions represent states of definite angular momentum, rather than of definite (linear) momentum, which are provided by plane waves $\exp(i \mathbf\cdot\mathbf)$.

Sphere with finite "square" potential

Consider the potential $V(r)=V_0$ for r and $V(r)=0$ elsewhere - that is, inside a sphere of radius $r_0$ the potential is equal to $V_0$ and it is zero outside the sphere. A potential with such a finite discontinuity is called a ''square potential.''A. Messiah, ''Quantum Mechanics'', vol. I, p. 78, North Holland Publishing Company, Amsterdam (1967). Translation from the French by G.M. Temmer

We first consider bound states, i.e. states which display the particle mostly inside the box (confined states). Those have an energy $E$ less than the potential outside the sphere, i.e., they have negative energy. Also worth noticing is that unlike Coulomb potential, featuring an infinite number of discrete bound states, the spherical square well has only a finite (if any) number because of its finite range.

The resolution essentially follows that of the vacuum case above with normalization of the total wavefunction added, solving two Schrödinger equations — inside and outside the sphere — of the previous kind, i.e., with constant potential. The following constraints must hold for a normalizable, physical wavefunction:

#The wavefunction must be regular at the origin.
#The wavefunction and its derivative must be continuous at the potential discontinuity.
#The wavefunction must converge at infinity.

The first constraint comes from the fact that Neumann and Hankel functions are singular at the origin. The physical requirement that $\psi$ must be defined everywhere selected Bessel function#Bessel functions of the first kind">Bessel function of the first kind over the other possibilities in the vacuum case. For the same reason, the solution will be of this kind inside the sphere:$R(r) = A j_\ell\left(\sqrtr\right), \qquad r < r_0.$Note that for bound states, $V_0 < E < 0$. Bound states bring the novelty as compared to the vacuum case now that $E<0$. This, along with the third constraint, selects the Hankel function of the first kind as the only converging solution at infinity (the singularity at the origin of these functions does not matter since we are now outside the sphere):$R(r) = Bh^_\ell\left(i\sqrtr\right), \qquad r>r_0$The second constraint on continuity of $\psi$ at $r=r_0$ along with normalization allows the determination of constants $A$ and $B$. Continuity of the derivative (or logarithmic derivative for convenience) requires quantization of energy.

Sphere with infinite "square" potential

In case where the potential well is infinitely deep, so that we can take $V_0=0$ inside the sphere and $\infty$ outside, the problem becomes that of matching the wavefunction inside the sphere (the spherical Bessel functions) with identically zero wavefunction outside the sphere. Allowed energies are those for which the radial wavefunction vanishes at the boundary. Thus, we use the zeros of the spherical Bessel functions to find the energy spectrum and wavefunctions. Calling $u_$ the ''k''^th zero of $j_\ell$, we have:$E_ = \frac$so that the problem is reduced to the computations of these zeros $u_$, typically by using a table or calculator, as these zeros are not solvable for the general case.

In the special case $\ell = 0$ (spherical symmetric orbitals), the spherical Bessel function is $j_0(x) = \frac$, which zeros can be easily given as $u_ = k \pi$. Their energy eigenvalues are thus:
$E_ = \frac = \frac$

3D isotropic harmonic oscillator

The potential of a 3D isotropic harmonic oscillator is
$V(r) = \frac m_0 \omega^2 r^2.$
An ''N''-dimensional isotropic harmonic oscillator has the energies
$E_n = \hbar \omega\left( n + \frac \right) \quad\text\quad n=0,1,\ldots,\infty,$
i.e., $n$ is a non-negative integral number; $\omega$ is the (same) fundamental frequency of the $N$ modes of the oscillator. In this case $N=3$, so that the radial Schrödinger equation becomes,
\left \frac \frac + +\frac m_0 \omega^2 r^2 - \hbar\omega\left(n+\tfrac\right) \rightu(r) = 0.

Introducing
$\gamma \equiv \frac$
and recalling that $u(r) = r R(r)$, we will show that the radial Schrödinger equation has the normalized solution,
$R_(r) = N_ \, r^ \, e^\; L^_(\gamma r^2),$
where the function $L^_k(\gamma r^2)$ is a generalized Laguerre polynomial in $yr^2$ of order $k$.

The normalization constant $N_$ is,
N_ = \left frac \right
\left frac \right .

The eigenfunction $R_(r)$ is associated with energy $E_n$, where
$\ell = n, n-2, \ldots, \ell_\min\quad \text\quad \ell_\min = \begin 1 & \text~ n~ \text \\ 0 & \text~ n~ \text \end$
This is the same result as the quantum harmonic oscillator, with $\gamma = 2 \nu$.

Derivation

First we transform the radial equation by a few successive substitutions to the generalized Laguerre differential equation, which has known solutions: the generalized Laguerre functions. Then we normalize the generalized Laguerre functions to unity. This normalization is with the usual volume element .

First we scale the radial coordinate
$y = \sqrtr \quad \text\quad \gamma \equiv \frac,$
and then the equation becomes
\left frac - \frac - y^2 + 2n + 3 \rightv(y) = 0
with $v(y) = u \left(y / \sqrt \right)$.

Consideration of the limiting behavior of at the origin and at infinity suggests the following substitution for ,
$v(y) = y^ e^ f(y).$
This substitution transforms the differential equation to
\left frac + 2 \left(\frac-y\right)\frac + 2n - 2\ell \rightf(y) = 0,
where we divided through with $y^ e^$, which can be done so long as ''y'' is not zero.

=Transformation to Laguerre polynomials

=
If the substitution $x = y^2$ is used, $y = \sqrt$, and the differential operators become
$\frac = \frac\frac = 2 y \frac = 2 \sqrt \frac,$ and
$\frac = \frac \left( 2 y \frac \right) = 4 x \frac + 2 \frac.$

The expression between the square brackets multiplying $f(y)$ becomes the differential equation characterizing the generalized Laguerre equation (see also Kummer's equation):
$x\frac + \left( \left(\ell+\frac\right) + 1 - x\right) \frac + \frac (n - \ell) g(x) = 0$
with $g(x) \equiv f(\sqrt)$.

Provided $k \equiv (n-\ell)/2$ is a non-negative integral number, the solutions of this equations are generalized (associated) Laguerre polynomials
$g(x) = L_k^(x).$

From the conditions on $k$ follows: (i) $n \ge \ell$ and (ii) $n$ and $l$ are either both odd or both even. This leads to the condition on $l$ given above.

=Recovery of the normalized radial wavefunction

=
Remembering that $u(r) = r R(r)$, we get the normalized radial solution:
$R_(r) = N_ \, r^ \, e^\; L^_(\gamma r^2).$

The normalization condition for the radial wave function is:
$\int^\infty_0 r^2 , R(r), ^2 \, dr = 1.$

Substituting $q = \gamma r^2$, gives $dq = 2 \gamma r \, dr$ and the equation becomes:
\frac
\int^\infty_0 q^ e^ \left L^_(q) \right 2 \, dq = 1.

By making use of the orthogonality properties of the generalized Laguerre polynomials, this equation simplifies to:
$\frac \cdot \frac = 1.$

Hence, the normalization constant can be expressed as:
$N_ = \sqrt$

Other forms of the normalization constant can be derived by using properties of the gamma function, while noting that $n$ and $l$ are both of the same parity. This means that $n+l$ is always even, so that the gamma function becomes:
\Gamma \left frac + \left( \frac + 1 \right) \right= \frac
= \frac,
where we used the definition of the double factorial. Hence, the normalization constant is also given by:
N_
= \left \frac \right
= \sqrt \left( \frac \right )^ \,()^ \, \sqrt.

Hydrogen-like atoms

A hydrogenic (hydrogen-like) atom is a two-particle system consisting of a nucleus and an electron. The two particles interact through the potential given by Coulomb's law:
$V(r) = -\frac \frac$
where
* ''ε''₀ is the permittivity of the vacuum,
* ''Z'' is the atomic number (''eZ'' is the charge of the nucleus),
* ''e'' is the elementary charge (charge of the electron),
* ''r'' is the distance between the electron and the nucleus.

In order to simplify the Schrödinger equation, we introduce the following constants that define the atomic unit of energy and length:

$E_\textrm = \mu \left( \frac\right)^2 \quad\text\quad a_0 = .$

where $\mu \approx m_e$ is the reduced mass in the $m_e \ll m_$ limit. Substitute $y = Zr/a_0$ and $W = E/(Z^2 E_\textrm)$ into the radial Schrödinger equation given above. This gives an equation in which all natural constants are hidden,
\left -\frac \frac + \frac \frac - \frac\rightu_\ell = W u_\ell .
Two classes of solutions of this equation exist:

(i) $W$ is negative, the corresponding eigenfunctions are square-integrable and the values of $W$ are quantized (discrete spectrum).

(ii) $W$ is non-negative, every real non-negative value of $W$ is physically allowed (continuous spectrum), the corresponding eigenfunctions are non-square integrable. Considering only class (i) solutions restricts the solutions to wavefunctions which are bound states, in contrast to the class (ii) solutions that are known as ''scattering states''.

For class (i) solutions with negative ''W'' the quantity $\alpha \equiv 2\sqrt$ is real and positive. The scaling of $y$, i.e., substitution of $x \equiv \alpha y$ gives the Schrödinger equation:
\left \frac -\frac + \frac - \frac \rightu_\ell = 0,
\quad \text x \ge 0.

For $x \rightarrow \infty$ the inverse powers of ''x'' are negligible and the normalizable (and therefore, physical) solution for large $x$ is \exp x/2/math>. Similarly, for $x \rightarrow 0$ the inverse square power dominates and the physical solution for small $x$ is ''x''^''ℓ''+1.
Hence, to obtain a full range solution we substitute
$u_l(x) = x^ e^f_\ell(x).$

The equation for $f_l(x)$ becomes,
\left x\frac + (2\ell+2-x) \frac +(n - \ell - 1)\rightf_\ell(x) = 0 \quad\text\quad n = (-2W)^=\frac.

Provided $n-\ell-1$ is a non-negative integer, this equation has polynomial solutions written as
$L^_(x),\qquad k=0,1,\ldots ,$
which are generalized Laguerre polynomials of order $k$. The energy becomes$W = -\frac\quad \text\quad n \equiv k+\ell+1 .$

The principal quantum number $n$ satisfies $n \ge \ell+1$. Since $\alpha = 2/n$, the total radial wavefunction is
$R_(r) = \frac = N_ \left(\frac\right)^\; e^\; L^_\left(\frac\right),$
with normalization which absorbs extra terms from $\frac$
N_ = \left left(\frac\right)^3 \cdot \frac\right,
viaH. Margenau and G. M. Murphy, ''The Mathematics of Physics and Chemistry'', Van Nostrand, 2nd edition (1956), p. 130. Note that convention of the Laguerre polynomial in this book differs from the present one. If we indicate the Laguerre in the definition of Margenau and Murphy with a bar on top, we have $\bar^_ = (-1)^k (n+k)! L^_n$.

\int_0^\infty x^ e^ \left L^_(x)\right2 dx =
\frac .

The corresponding energy is
$E = - \fracE_\textrm,\qquad n=1,2,\ldots .$

References

{{DEFAULTSORT:Particle In A Spherically Symmetric Potential
Partial differential equations
Quantum models