Octonion multiplication on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, the octonions are a
 A variation of this sometimes used is to label the elements of the basis by the elements , 0, 1, 2, ..., 6, of the
A variation of this sometimes used is to label the elements of the basis by the elements , 0, 1, 2, ..., 6, of the
ArXive preprint
Figure 1 is locate
here
The multiplication table for a geometric algebra of signature can be given in terms of the following 7 quaternionic triples (omitting the identity element): : in which the lowercase items are vectors and the uppercase ones are

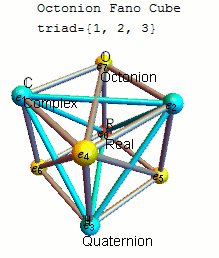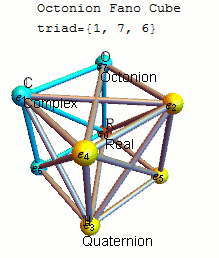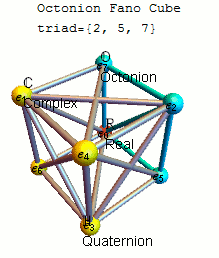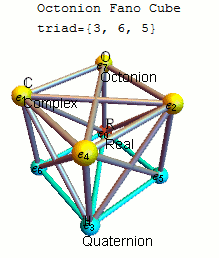 A convenient
A convenient
Review
. * * * * * * * *
* * {{Authority control Composition algebras
normed division algebra
In mathematics, Hurwitz's theorem is a theorem of Adolf Hurwitz (1859–1919), published posthumously in 1923, solving the Hurwitz problem for finite-dimensional unital real non-associative algebras endowed with a positive-definite quadratic f ...
over the real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s, a kind of hypercomplex number system
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
. The octonions are usually represented by the capital letter O, using boldface or blackboard bold
Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol (usually vertical or near-vertical lines) are doubled. The symbols usually denote number sets. One way of pro ...
. Octonions have eight dimensions
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordin ...
; twice the number of dimensions of the quaternions, of which they are an extension. They are noncommutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name o ...
and nonassociative, but satisfy a weaker form of associativity; namely, they are alternative
Alternative or alternate may refer to:
Arts, entertainment and media
* Alternative (''Kamen Rider''), a character in the Japanese TV series ''Kamen Rider Ryuki''
* ''The Alternative'' (film), a 1978 Australian television film
* ''The Alternative ...
. They are also power associative In mathematics, specifically in abstract algebra, power associativity is a property of a binary operation that is a weak form of associativity.
Definition
An algebra (or more generally a magma) is said to be power-associative if the subalgebra ...
.
Octonions are not as well known as the quaternions and complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s, which are much more widely studied and used. Octonions are related to exceptional structures in mathematics, among them the exceptional Lie group
In mathematics, a simple Lie group is a connected non-abelian Lie group ''G'' which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symm ...
s. Octonions have applications in fields such as string theory, special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The laws ...
and quantum logic
In the mathematical study of logic and the physical analysis of quantum foundations, quantum logic is a set of rules for manipulation of propositions inspired by the structure of quantum theory. The field takes as its starting point an observ ...
. Applying the Cayley–Dickson construction
In mathematics, the Cayley–Dickson construction, named after Arthur Cayley and Leonard Eugene Dickson, produces a sequence of algebras over the field of real numbers, each with twice the dimension of the previous one. The algebras produced b ...
to the octonions produces the sedenion
In abstract algebra, the sedenions form a 16-dimensional noncommutative and nonassociative algebra over the real numbers; they are obtained by applying the Cayley–Dickson construction to the octonions, and as such the octonions are isomorphic to ...
s.
History
The octonions were discovered in 1843 by John T. Graves, inspired by his friendWilliam Rowan Hamilton
Sir William Rowan Hamilton LL.D, DCL, MRIA, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the Andrews Professor of Astronomy at Trinity College Dublin, and Royal Astronomer of Irela ...
's discovery of quaternions. Graves called his discovery "octaves", and mentioned them in a letter to Hamilton dated 26 December 1843. He first published his result slightly later than Arthur Cayley's article. The octonions were discovered independently by Cayley and are sometimes referred to as "Cayley numbers" or the "Cayley algebra". Hamilton described the early history of Graves' discovery.
Definition
The octonions can be thought of as octets (or 8-tuples) of real numbers. Every octonion is a real linear combination of the unit octonions: : where is the scalar or real element; it may be identified with the real number 1. That is, every octonion can be written in the form : with real coefficients . Addition and subtraction of octonions is done by adding and subtracting corresponding terms and hence their coefficients, like quaternions. Multiplication is more complex. Multiplication is distributive over addition, so the product of two octonions can be calculated by summing the products of all the terms, again like quaternions. The product of each pair of terms can be given by multiplication of the coefficients and amultiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essenti ...
of the unit octonions, like this one (due to Cayley, 1845, and Graves, 1843):
Most off-diagonal elements of the table are antisymmetric, making it almost a skew-symmetric matrix
In mathematics, particularly in linear algebra, a skew-symmetric (or antisymmetric or antimetric) matrix is a square matrix whose transpose equals its negative. That is, it satisfies the condition
In terms of the entries of the matrix, if ...
except for the elements on the main diagonal, as well as the row and column for which is an operand.
The table can be summarized as follows:
:
where is the Kronecker delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
\delta_ = \begin
0 &\text i \neq j, \\
1 & ...
(equal to 1 if and only if ), and is a completely antisymmetric tensor In mathematics and theoretical physics, a tensor is antisymmetric on (or with respect to) an index subset if it alternates sign (+/−) when any two indices of the subset are interchanged. section §7. The index subset must generally either be all ' ...
with value 1 when .
The above definition is not unique, however; it is only one of 480 possible definitions for octonion multiplication with . The others can be obtained by permuting and changing the signs of the non-scalar basis elements . The 480 different algebras are isomorphic, and there is rarely a need to consider which particular multiplication rule is used.
Each of these 480 definitions is invariant up to signs under some 7-cycle of the points (1234567), and for each 7-cycle there are four definitions, differing by signs and reversal of order. A common choice is to use the definition invariant under the 7-cycle (1234567) with — by using the triangular multiplication diagram, or Fano plane below that also shows the sorted list of 124 based 7-cycle triads and its associated multiplication matrices in both and IJKL format.
:projective line
In mathematics, a projective line is, roughly speaking, the extension of a usual line by a point called a ''point at infinity''. The statement and the proof of many theorems of geometry are simplified by the resultant elimination of special cases; ...
over the finite field
In mathematics, a finite field or Galois field (so-named in honor of Évariste Galois) is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtr ...
of order 7. The multiplication is then given by and , and all expressions obtained from this by adding a constant ( modulo 7) to all subscripts: in other words using the seven triples (124) (235) (346) (450) (561) (602) (013). These are the nonzero codewords of the quadratic residue code
A quadratic residue code is a type of cyclic code.
Examples
Examples of quadratic
residue codes include the (7,4) Hamming code
over GF(2), the (23,12) binary Golay code
over GF(2) and the (11,6) ternary Golay code
over GF(3).
Constructions
There ...
of length 7 over the Galois field
In mathematics, a finite field or Galois field (so-named in honor of Évariste Galois) is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtr ...
of two elements, . There is a symmetry of order 7 given by adding a constant mod 7 to all subscripts, and also a symmetry of order 3 given by multiplying all subscripts by one of the quadratic residues 1, 2, 4 mod 7.. Available aArXive preprint
Figure 1 is locate
here
The multiplication table for a geometric algebra of signature can be given in terms of the following 7 quaternionic triples (omitting the identity element): : in which the lowercase items are vectors and the uppercase ones are
bivector In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalars and vectors. If a scalar is considered a degree-zero quantity, and a vector is a degree-one quantity, then a bivector ca ...
s and (which is the Hodge star operator
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the ...
). If the is forced to be equal to the identity then the multiplication ceases to be associative, but the may be removed from the multiplication table resulting in an octonion multiplication table.
In keeping associative and thus not reducing the 4-dimensional geometric algebra to an octonion one, the whole multiplication table can be derived from the equation for . Consider the gamma matrices
In mathematical physics, the gamma matrices, \left\ , also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra Cl1,3(\ma ...
. The formula defining the fifth gamma matrix shows that it is the of a four-dimensional geometric algebra of the gamma matrices.
Cayley–Dickson construction
A more systematic way of defining the octonions is via the Cayley–Dickson construction. Just as quaternions can be defined as pairs of complex numbers, the octonions can be defined as pairs of quaternions. Addition is defined pairwise. The product of two pairs of quaternions and is defined by : where denotes the conjugate of the quaternion . This definition is equivalent to the one given above when the eight unit octonions are identified with the pairs :Fano plane mnemonic
 A convenient
A convenient mnemonic
A mnemonic ( ) device, or memory device, is any learning technique that aids information retention or retrieval (remembering) in the human memory for better understanding.
Mnemonics make use of elaborative encoding, retrieval cues, and imag ...
for remembering the products of unit octonions is given by the diagram, which represents the multiplication table of Cayley and Graves. Figure 29.1: Representation of multiplication table on projective plane. This diagram with seven points and seven lines (the circle through 1, 2, and 3 is considered a line) is called the Fano plane
In finite geometry, the Fano plane (after Gino Fano) is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines ...
. The lines are directional. The seven points correspond to the seven standard basis elements of (see definition below). Each pair of distinct points lies on a unique line and each line runs through exactly three points.
Let be an ordered triple of points lying on a given line with the order specified by the direction of the arrow. Then multiplication is given by
: and
together with cyclic permutation
In mathematics, and in particular in group theory, a cyclic permutation (or cycle) is a permutation of the elements of some set ''X'' which maps the elements of some subset ''S'' of ''X'' to each other in a cyclic fashion, while fixing (that is, ma ...
s. These rules together with
*1 is the multiplicative identity,
* for each point in the diagram
completely defines the multiplicative structure of the octonions. Each of the seven lines generates a subalgebra In mathematics, a subalgebra is a subset of an algebra, closed under all its operations, and carrying the induced operations.
"Algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operat ...
of isomorphic to the quaternions .
Conjugate, norm, and inverse
The ''conjugate'' of an octonion : is given by : Conjugation is aninvolution
Involution may refer to:
* Involute, a construction in the differential geometry of curves
* '' Agricultural Involution: The Processes of Ecological Change in Indonesia'', a 1963 study of intensification of production through increased labour inpu ...
of and satisfies (note the change in order).
The ''real part'' of is given by
:
and the ''imaginary part'' by
:
The set of all purely imaginary octonions span
Span may refer to:
Science, technology and engineering
* Span (unit), the width of a human hand
* Span (engineering), a section between two intermediate supports
* Wingspan, the distance between the wingtips of a bird or aircraft
* Sorbitan ester ...
a 7- dimensional subspace of , denoted .
Conjugation of octonions satisfies the equation
:
The product of an octonion with its conjugate, , is always a nonnegative real number:
:
Using this the norm of an octonion can be defined, as
:
This norm agrees with the standard 8-dimensional Euclidean norm on .
The existence of a norm on implies the existence of inverses for every nonzero element of . The inverse of , which is the unique octonion satisfying , is given by
:
Properties
Octonionic multiplication is neithercommutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of ...
:
: if , are distinct and non-zero,
nor associative:
: if , , are distinct, non-zero and .
The octonions do satisfy a weaker form of associativity: they are alternative. This means that the subalgebra generated by any two elements is associative. Actually, one can show that the subalgebra generated by any two elements of is isomorphic to , , or , all of which are associative. Because of their non-associativity, octonions cannot be represented by a subalgebra of a matrix ring over , unlike the real numbers, complex numbers and quaternions.
The octonions do retain one important property shared by , , and : the norm on satisfies
:
This equation means that the octonions form a composition algebra
In mathematics, a composition algebra over a field is a not necessarily associative algebra over together with a nondegenerate quadratic form that satisfies
:N(xy) = N(x)N(y)
for all and in .
A composition algebra includes an involution ...
. The higher-dimensional algebras defined by the Cayley–Dickson construction (starting with the sedenion
In abstract algebra, the sedenions form a 16-dimensional noncommutative and nonassociative algebra over the real numbers; they are obtained by applying the Cayley–Dickson construction to the octonions, and as such the octonions are isomorphic to ...
s) all fail to satisfy this property. They all have zero divisor
In abstract algebra, an element of a ring is called a left zero divisor if there exists a nonzero in such that , or equivalently if the map from to that sends to is not injective. Similarly, an element of a ring is called a right zer ...
s.
Wider number systems exist which have a multiplicative modulus (for example, 16-dimensional conic sedenions). Their modulus is defined differently from their norm, and they also contain zero divisors.
As shown by Hurwitz
Hurwitz is one of the variants of a surname of Ashkenazi Jewish origin (for historical background see the Horowitz page).
Notable people with the surname include:
*Adolf Hurwitz (1859–1919), German mathematician
** Hurwitz polynomial
**Hurwitz m ...
, , , , and are the only normed division algebras over the real numbers. These four algebras also form the only alternative, finite-dimensional division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field in which division, except by zero, is always possible.
Definitions
Formally, we start with a non-zero algebra ''D'' over a fie ...
s over the real numbers ( up to isomorphism).
Not being associative, the nonzero elements of do not form a group
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic ide ...
. They do, however, form a loop
Loop or LOOP may refer to:
Brands and enterprises
* Loop (mobile), a Bulgarian virtual network operator and co-founder of Loop Live
* Loop, clothing, a company founded by Carlos Vasquez in the 1990s and worn by Digable Planets
* Loop Mobile, an ...
, specifically a Moufang loop Moufang is the family name of the following people:
* Christoph Moufang (1817–1890), a Roman Catholic cleric
* Ruth Moufang (1905–1977), a German mathematician, after whom several concepts in mathematics are named:
** Moufang–Lie algebra
** ...
.
Commutator and cross product
The commutator of two octonions and is given by : This is antisymmetric and imaginary. If it is considered only as a product on the imaginary subspace it defines a product on that space, theseven-dimensional cross product
In mathematics, the seven-dimensional cross product is a bilinear operation on vectors in seven-dimensional Euclidean space. It assigns to any two vectors a, b in a vector also in .
Like the cross product in three dimensions, the seven-dim ...
, given by
:
Like the cross product in three dimensions this is a vector orthogonal to and with magnitude
:
But like the octonion product it is not uniquely defined. Instead there are many different cross products, each one dependent on the choice of octonion product.
Automorphisms
An automorphism, , of the octonions is an invertiblelinear transformation
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that pre ...
of which satisfies
:
The set of all automorphisms of forms a group called . The group is a simply connected, compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact
* Blood compact, an ancient ritual of the Philippines
* Compact government, a type of colonial rule utilized in British ...
, real Lie group of dimension 14. This group is the smallest of the exceptional Lie groups and is isomorphic to the subgroup
In group theory, a branch of mathematics, given a group ''G'' under a binary operation ∗, a subset ''H'' of ''G'' is called a subgroup of ''G'' if ''H'' also forms a group under the operation ∗. More precisely, ''H'' is a subgroup ...
of that preserves any chosen particular vector in its 8-dimensional real spinor representation. The group is in turn a subgroup of the group of isotopies described below.
''See also'': – the automorphism group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the g ...
of the Fano plane.
Isotopies
Anisotopy of an algebra In mathematics, an isotopy from a possibly non-associative algebra ''A'' to another is a triple of bijective linear maps such that if then . This is similar to the definition of an isotopy of loops, except that it must also preserve the linear str ...
is a triple of bijective
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other ...
linear maps , , such that if then . For this is the same as an automorphism. The isotopy group of an algebra is the group of all isotopies, which contains the group of automorphisms as a subgroup.
The isotopy group of the octonions is the group , with , , acting as the three 8-dimensional representations. The subgroup of elements where fixes the identity is the subgroup , and the subgroup where , , all fix the identity is the automorphism group .
Applications
The octonions play a significant role in the classification and construction of other mathematical entities. For example, theexceptional Lie group
In mathematics, a simple Lie group is a connected non-abelian Lie group ''G'' which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symm ...
is the automorphism group of the octonions, and the other exceptional Lie groups , , and can be understood as the isometries of certain projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that d ...
s defined using the octonions. The set of self-adjoint
In mathematics, and more specifically in abstract algebra, an element ''x'' of a *-algebra is self-adjoint if x^*=x. A self-adjoint element is also Hermitian, though the reverse doesn't necessarily hold.
A collection ''C'' of elements of a st ...
3 × 3 octonionic matrices
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** ''The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchis ...
, equipped with a symmetrized matrix product, defines the Albert algebra. In discrete mathematics, the octonions provide an elementary derivation of the Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space, which is one of the best models for the kissing number problem. It was discovered by . It may also have been discovered (but not published) by ...
, and thus they are closely related to the sporadic simple groups
In mathematics, a sporadic group is one of the 26 exceptional groups found in the classification of finite simple groups.
A simple group is a group ''G'' that does not have any normal subgroups except for the trivial group and ''G'' itself. The ...
.
Applications of the octonions to physics have largely been conjectural. For example, in the 1970s, attempts were made to understand quarks by way of an octonionic Hilbert space. It is known that the octonions, and the fact that only four normed division algebras can exist, relates to the spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differ ...
dimensions in which supersymmetric
In a supersymmetric theory the equations for force and the equations for matter are identical. In theoretical and mathematical physics, any theory with this property has the principle of supersymmetry (SUSY). Dozens of supersymmetric theories ...
quantum field theories
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles ...
can be constructed. Also, attempts have been made to obtain the Standard Model of elementary particle physics from octonionic constructions, for example using the "Dixon algebra" .
Octonions have also arisen in the study of black hole entropy
In physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons. As the study of the statistical mechanics of black-body radiation led to the development ...
, quantum information science
Quantum information science is an interdisciplinary field that seeks to understand the analysis, processing, and transmission of information using quantum mechanics principles. It combines the study of Information science with quantum effects in ...
, and string theory.
Octonions have been used in solutions to the hand eye calibration problem
In robotics and mathematics, the hand eye calibration problem (also called the robot-sensor or robot-world calibration problem) is the problem of determining the transformation between a robot end-effector and a sensor or sensors (camera or laser s ...
in robotics
Robotics is an interdisciplinary branch of computer science and engineering. Robotics involves design, construction, operation, and use of robots. The goal of robotics is to design machines that can help and assist humans. Robotics integrate ...
.
Deep octonion networks provide a means of efficient and compact expression in machine learning applications.
Integral octonions
There are several natural ways to choose an integral form of the octonions. The simplest is just to take the octonions whose coordinates areinteger
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
s. This gives a nonassociative algebra over the integers called the Gravesian octonions. However it is not a maximal order (in the sense of ring theory); there are exactly seven maximal orders containing it. These seven maximal orders are all equivalent under automorphisms. The phrase "integral octonions" usually refers to a fixed choice of one of these seven orders.
These maximal orders were constructed by , Dickson and Bruck as follows. Label the eight basis vectors by the points of the projective line over the field with seven elements. First form the "Kirmse integers" : these consist of octonions whose coordinates are integers or half integers, and that are half integers (that is, halves of odd integers) on one of the 16 sets
:
of the extended quadratic residue code
A quadratic residue code is a type of cyclic code.
Examples
Examples of quadratic
residue codes include the (7,4) Hamming code
over GF(2), the (23,12) binary Golay code
over GF(2) and the (11,6) ternary Golay code
over GF(3).
Constructions
There ...
of length 8 over the field of two elements, given by , and its images under adding a constant modulo 7, and the complements of these eight sets. Then switch infinity and any one other coordinate; this operation creates a bijection of the Kirmse integers onto a different set, which is a maximal order. There are seven ways to do this, giving seven maximal orders, which are all equivalent under cyclic permutations of the seven coordinates 0123456. (Kirmse incorrectly claimed that the Kirmse integers also form a maximal order, so he thought there were eight maximal orders rather than seven, but as pointed out they are not closed under multiplication; this mistake occurs in several published papers.)
The Kirmse integers and the seven maximal orders are all isometric to the lattice rescaled by a factor of . In particular there are 240 elements of minimum nonzero norm 1 in each of these orders, forming a Moufang loop of order 240.
The integral octonions have a "division with remainder" property: given integral octonions and , we can find and with , where the remainder has norm less than that of .
In the integral octonions, all left ideals and right ideals are 2-sided ideals, and the only 2-sided ideals are the principal ideal
In mathematics, specifically ring theory, a principal ideal is an ideal I in a ring R that is generated by a single element a of R through multiplication by every element of R. The term also has another, similar meaning in order theory, where ...
s where is a non-negative integer.
The integral octonions have a version of factorization into primes, though it is not straightforward to state because the octonions are not associative so the product of octonions depends on the order in which one does the products. The irreducible integral octonions are exactly those of prime norm, and every integral octonion can be written as a product of irreducible octonions. More precisely an integral octonion of norm can be written as a product of integral octonions of norms and .
The automorphism group of the integral octonions is the group of order 12,096, which has a simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by Johnn ...
subgroup of index 2 isomorphic to the unitary group . The isotopy group of the integral octonions is the perfect double cover of the group of rotations of the lattice.
See also
*Octonion algebra In mathematics, an octonion algebra or Cayley algebra over a field ''F'' is a composition algebra over ''F'' that has dimension 8 over ''F''. In other words, it is a unital non-associative algebra ''A'' over ''F'' with a non-degenerate quadratic ...
*Okubo algebra In abstract algebra, algebra, an Okubo algebra or pseudo-octonion algebra is an 8-dimensional algebra over a field, non-associative algebra similar to the one studied by Susumu Okubo. Okubo algebras are composition algebras, flexible algebras (''A'' ...
*
* Split-octonions
*Triality
In mathematics, triality is a relationship among three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin( ...
Notes
References
* * * .Review
. * * * * * * * *
External links
* Koutsoukou-Argyraki, Angeliki* * {{Authority control Composition algebras