Non-linear Artillery

In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one.
In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the unknown variables or functions that appear in them. Systems can be defined as nonlinear, regardless of whether known linear functions appear in the equations. In particular, a differential equation is ''linear'' if it is linear in terms of the unknown function and its derivatives, even if nonlinear in terms of the other variables appearing in it.

As nonlinear dynamical equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization). This works well up to some accuracy and some range for the input values, but some interesting phenomena such as solitons, chaos, and singularities are hidden by linearization. It follows that some aspects of the dynamic behavior of a nonlinear system can appear to be counterintuitive, unpredictable or even chaotic. Although such chaotic behavior may resemble random behavior, it is in fact not random. For example, some aspects of the weather are seen to be chaotic, where simple changes in one part of the system produce complex effects throughout. This nonlinearity is one of the reasons why accurate long-term forecasts are impossible with current technology.

Some authors use the term nonlinear science for the study of nonlinear systems. This term is disputed by others:

Definition

In mathematics, a linear map (or ''linear function'') $f(x)$ is one which satisfies both of the following properties:
*Additivity or superposition principle: $\textstyle f(x + y) = f(x) + f(y);$
*Homogeneity: $\textstyle f(\alpha x) = \alpha f(x).$

Additivity implies homogeneity for any rational ''α'', and, for continuous functions, for any real ''α''. For a complex ''α'', homogeneity does not follow from additivity. For example, an antilinear map is additive but not homogeneous. The conditions of additivity and homogeneity are often combined in the superposition principle
:$f(\alpha x + \beta y) = \alpha f(x) + \beta f(y)$

An equation written as
:$f(x) = C$

is called linear if $f(x)$ is a linear map (as defined above) and nonlinear otherwise. The equation is called ''homogeneous'' if $C = 0$.

The definition $f(x) = C$ is very general in that $x$ can be any sensible mathematical object (number, vector, function, etc.), and the function $f(x)$ can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If $f(x)$ contains differentiation with respect to $x$, the result will be a differential equation.

Nonlinear algebraic equations

Nonlinear algebraic equations, which are also called ''polynomial equations'', are defined by equating polynomials (of degree greater than one) to zero. For example,
:$x^2 + x - 1 = 0\,.$

For a single polynomial equation, root-finding algorithms can be used to find solutions to the equation (i.e., sets of values for the variables that satisfy the equation). However, systems of algebraic equations are more complicated; their study is one motivation for the field of algebraic geometry, a difficult branch of modern mathematics. It is even difficult to decide whether a given algebraic system has complex solutions (see Hilbert's Nullstellensatz). Nevertheless, in the case of the systems with a finite number of complex solutions, these systems of polynomial equations are now well understood and efficient methods exist for solving them.

Nonlinear recurrence relations

A nonlinear recurrence relation defines successive terms of a sequence as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map and the relations that define the various Hofstadter sequences. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related nonlinear system identification and analysis procedures.Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains". Wiley, 2013 These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains.

Nonlinear differential equations

A system of differential equations is said to be nonlinear if it is not a system of linear equations. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics and the Lotka–Volterra equations in biology.

One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions.

Ordinary differential equations

First order ordinary differential equations are often exactly solvable by separation of variables, especially for autonomous equations. For example, the nonlinear equation
:$\frac = -u^2$

has $u=\frac$ as a general solution (and also $u = 0$ as a particular solution, corresponding to the limit of the general solution when ''C'' tends to infinity). The equation is nonlinear because it may be written as
:$\frac + u^2=0$

and the left-hand side of the equation is not a linear function of $u$ and its derivatives. Note that if the $u^2$ term were replaced with $u$, the problem would be linear (the exponential decay problem).

Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed-form solutions, though implicit solutions and solutions involving nonelementary integrals are encountered.

Common methods for the qualitative analysis of nonlinear ordinary differential equations include:

*Examination of any conserved quantities, especially in Hamiltonian systems
*Examination of dissipative quantities (see Lyapunov function) analogous to conserved quantities
*Linearization via Taylor expansion
*Change of variables into something easier to study
* Bifurcation theory
* Perturbation methods (can be applied to algebraic equations too)
*Existence of solutions of Finite-Duration, which can happen under specific conditions for some non-linear ordinary differential equations.

Partial differential equations

The most common basic approach to studying nonlinear partial differential equations is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly linear). Sometimes, the equation may be transformed into one or more ordinary differential equations, as seen in separation of variables, which is always useful whether or not the resulting ordinary differential equation(s) is solvable.

Another common (though less mathematical) tactic, often exploited in fluid and heat mechanics, is to use scale analysis to simplify a general, natural equation in a certain specific boundary value problem. For example, the (very) nonlinear Navier-Stokes equations can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation.

Other methods include examining the characteristics and using the methods outlined above for ordinary differential equations.

Pendula

A classic, extensively studied nonlinear problem is the dynamics of a frictionless pendulum under the influence of gravity. Using Lagrangian mechanics, it may be shownDavid Tong: Lectures on Classical Dynamics
/ref> that the motion of a pendulum can be described by the dimensionless nonlinear equation
:$\frac + \sin(\theta) = 0$

where gravity points "downwards" and $\theta$ is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use $d\theta/dt$ as an integrating factor, which would eventually yield
:$\int = t + C_1$

which is an implicit solution involving an elliptic integral. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral (nonelementary unless $C_0 = 2$).

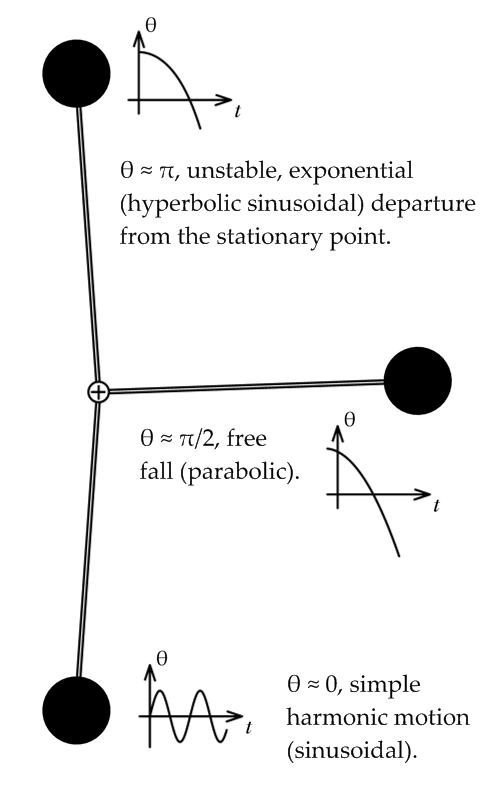
Another way to approach the problem is to linearize any nonlinearity (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at $\theta = 0$, called the small angle approximation, is
:$\frac + \theta = 0$

since $\sin(\theta) \approx \theta$ for $\theta \approx 0$. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at $\theta = \pi$, corresponding to the pendulum being straight up:
:$\frac + \pi - \theta = 0$

since $\sin(\theta) \approx \pi - \theta$ for $\theta \approx \pi$. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that $, \theta,$ will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state.

One more interesting linearization is possible around $\theta = \pi/2$, around which $\sin(\theta) \approx 1$:
:$\frac + 1 = 0.$

This corresponds to a free fall problem. A very useful qualitative picture of the pendulum's dynamics may be obtained by piecing together such linearizations, as seen in the figure at right. Other techniques may be used to find (exact) phase portraits and approximate periods.

Types of nonlinear dynamic behaviors

* Amplitude death – any oscillations present in the system cease due to some kind of interaction with other system or feedback by the same system
* Chaos – values of a system cannot be predicted indefinitely far into the future, and fluctuations are aperiodic
* Multistability – the presence of two or more stable states
* Solitons – self-reinforcing solitary waves
*Limit cycles – asymptotic periodic orbits to which destabilized fixed points are attracted.
* Self-oscillations – feedback oscillations taking place in open dissipative physical systems.

Examples of nonlinear equations

* Algebraic Riccati equation
*Ball and beam system
* Bellman equation for optimal policy
* Boltzmann equation
* Colebrook equation
* General relativity
* Ginzburg–Landau theory
* Ishimori equation
* Kadomtsev–Petviashvili equation
* Korteweg–de Vries equation
* Landau–Lifshitz–Gilbert equation
*Liénard equation
* Navier–Stokes equations of fluid dynamics
* Nonlinear optics
* Nonlinear Schrödinger equation
* Power-flow study
* Richards equation for unsaturated water flow
* Self-balancing unicycle
*Sine-Gordon equation
* Van der Pol oscillator
* Vlasov equation

See also

*Aleksandr Mikhailovich Lyapunov
* Dynamical system
*Feedback
*Initial condition
* Linear system
* Mode coupling
*Vector soliton
* Volterra series

References

Further reading

*
*
*
*
*

External links

Command and Control Research Program (CCRP)
* ttp://ocw.mit.edu/courses/mathematics/18-353j-nonlinear-dynamics-i-chaos-fall-2012/ Nonlinear Dynamics I: Chaosa
MIT's OpenCourseWare
(in MATLAB) a Database of Physical Systems
The Center for Nonlinear Studies at Los Alamos National Laboratory

{{Authority control

Dynamical systems
Concepts in physics