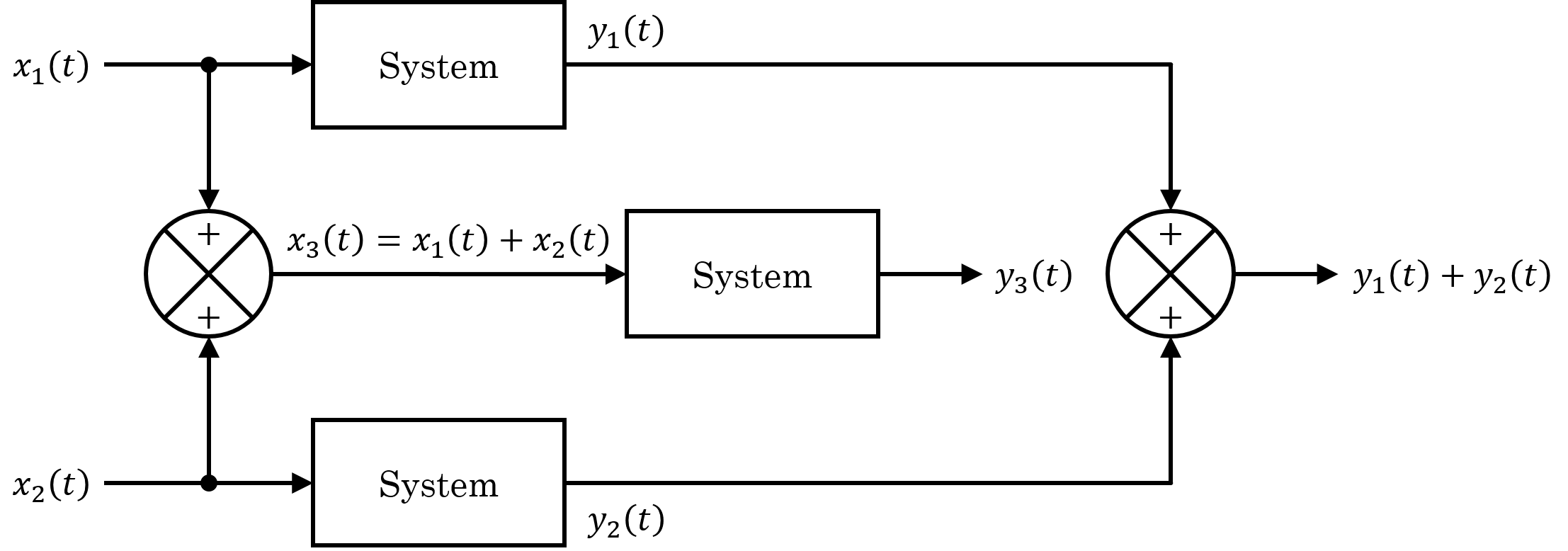
|
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, that maps an input, as a function of to an output, a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear combination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Systems Theory
Systems theory is the interdisciplinary study of systems, i.e. cohesive groups of interrelated, interdependent components that can be natural or human-made. Every system has causal boundaries, is influenced by its context, defined by its structure, function and role, and expressed through its relations with other systems. A system is "more than the sum of its parts" by expressing synergy or emergent behavior. Changing one component of a system may affect other components or the whole system. It may be possible to predict these changes in patterns of behavior. For systems that learn and adapt, the growth and the degree of adaptation depend upon how well the system is engaged with its environment and other contexts influencing its organization. Some systems support other systems, maintaining the other system to prevent failure. The goals of systems theory are to model a system's dynamics, constraints, conditions, and relations; and to elucidate principles (such as purpose, measure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Response
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components (such as microphones, amplifiers and loudspeakers) so that the overall response is as flat (uniform) as possible across the system's bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog and digital filters. The frequency response characterizes systems in the frequency domain, just as the impulse response characterizes systems in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. It has two major branches, differential calculus and integral calculus; the former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus, and they make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. Infinitesimal calculus was developed independently in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz. Later work, including (ε, δ)-definition of limit, codify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Differential Equation
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y + a_1(x)y' + a_2(x)y'' \cdots + a_n(x)y^ = b(x) where and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of an unknown function of the variable . Such an equation is an ordinary differential equation (ODE). A ''linear differential equation'' may also be a linear partial differential equation (PDE), if the unknown function depends on several variables, and the derivatives that appear in the equation are partial derivatives. A linear differential equation or a system of linear equations such that the associated homogeneous equations have constant coefficients may be solved by quadrature, which means that the solutions may be expressed in terms of integrals. This is also true for a linear equation of order one, with non-con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearization
In mathematics, linearization is finding the linear approximation to a function at a given point. The linear approximation of a function is the first order Taylor expansion around the point of interest. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or discrete dynamical systems. This method is used in fields such as engineering, physics, economics, and ecology. Linearization of a function Linearizations of a function are lines—usually lines that can be used for purposes of calculation. Linearization is an effective method for approximating the output of a function y = f(x) at any x = a based on the value and slope of the function at x = b, given that f(x) is differentiable on , b/math> (or , a/math>) and that a is close to b. In short, linearization approximates the output of a function near x = a. For example, \sqrt = 2. However, what would be a good appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (geometric)
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a '' directed line segment'', or graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \overrightarrow . A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word ''vector'' means "carrier". It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operations whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometimes applied to parts of the field of discrete mathematics that deals with finite se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain (z-domain or z-plane) representation. It can be considered as a discrete-time equivalent of the Laplace transform (s-domain). This similarity is explored in the theory of time-scale calculus. Whereas the continuous-time Fourier transform is evaluated on the Laplace s-domain's imaginary line, the discrete-time Fourier transform is evaluated over the unit circle of the z-domain. What is roughly the s-domain's left half-plane, is now the inside of the complex unit circle; what is the z-domain's outside of the unit circle, roughly corresponds to the right half-plane of the s-domain. One of the means of designing digital filters is to take analog designs, subject them to a bilinear transform which maps them from the s-domain to the z-domain, and then produce the digital filter by inspection, manipulation, or numeric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in ... that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex frequency domain, also known as ''s''-domain, or s-plane). The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions ''f'', the Laplace transform is the integral \mathcal\(s) = \int_0^\infty f(t)e^ \, dt. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
