|
Dimensionless
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another system, these quantities do not necessitate explicitly defined units. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific units of volume used, such as in milliliters per milliliter (mL/mL). The number one is recognized as a dimensionless base quantity. Radians serve as dimensionless units for angular measurements, derived from the universal ratio of 2π times the radius of a circle being equal to its circumference. Dimensionless quantities play a crucial role serving as parameters in differential equations in various technical disciplines. In calculus, concepts like the unitless ratios in limits or derivatives often involve dimensionless quantities. In differential geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an Circular arc, arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless unit, dimensionless SI derived unit,: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units." defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as . Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing. Definition One radian is defined as the angle at the center of a circle in a plane that wikt:subtend, subtends an arc whose length equals the radius of the circle. More generally, the magnit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base Unit Of Measurement
A base unit of measurement (also referred to as a base unit or fundamental unit) is a unit of measurement adopted for a '' base quantity''. A base quantity is one of a conventionally chosen subset of physical quantities, where no quantity in the subset can be expressed in terms of the others. The SI base units, or ''Systéme International d'unités'', consists of the metre, kilogram, second, ampere, kelvin, mole and candela. A unit multiple (or multiple of a unit) is an integer multiple of a given unit; likewise a unit submultiple (or submultiple of a unit) is a submultiple or a unit fraction of a given unit. ''Unit prefixes'' are common base-10 or base-2 powers multiples and submultiples of units. While a base unit is one that has been explicitly so designated, a derived unit is unit for a '' derived quantity'', involving the combination of quantities with different units; several ''SI derived units'' are specially named. A '' coherent derived unit'' involves no conversion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid dynamics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between Inertia, inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar flow, laminar (sheet-like) flow, while at high Reynolds numbers, flows tend to be turbulence, turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow (Eddy (fluid dynamics), eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar–turbulent transition, laminar to turbulent flow and is used in the scaling of similar but different-sized fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fine-structure Constant
In physics, the fine-structure constant, also known as the Sommerfeld constant, commonly denoted by (the Alpha, Greek letter ''alpha''), is a Dimensionless physical constant, fundamental physical constant that quantifies the strength of the electromagnetic interaction between elementary charged particles. It is a dimensionless quantity (dimensionless physical constant), independent of the system of units used, which is related to the strength of the coupling of an elementary charge ''e'' with the electromagnetic field, by the formula . Its numerical value is approximately , with a relative uncertainty of The constant was named by Arnold Sommerfeld, who introduced it in 1916 Equation 12a, ''"rund 7·" (about ...)'' when extending the Bohr model of the atom. quantified the gap in the fine structure of the spectral lines of the hydrogen atom, which had been measured precisely by Albert A. Michelson, Michelson and Edward W. Morley, Morley in 1887. Why the constant should have t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volumetric Ratio
In chemistry and fluid mechanics, the volume fraction \varphi_i is defined as the volume of a constituent ''V''''i'' divided by the volume of all constituents of the mixture ''V'' prior to mixing: :\varphi_i = \frac . Being dimensionless, its unit is 1; it is expressed as a number, e.g., 0.18. It is the same concept as volume percent (vol%) except that the latter is expressed with a denominator of 100, e.g., 18%. The volume fraction coincides with the ''volume concentration'' in ideal solutions where the volumes of the constituents are additive (the volume of the solution is equal to the sum of the volumes of its ingredients). The sum of all volume fractions of a mixture is equal to 1: :\sum_^ V_i = V ; \qquad \sum_^ \varphi_i = 1. The volume fraction (percentage by volume, vol%) is one way of expressing the composition of a mixture with a dimensionless quantity; mass fraction (percentage by weight, wt%) and mole fraction (percentage by moles, mol%) are others. Volume conc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
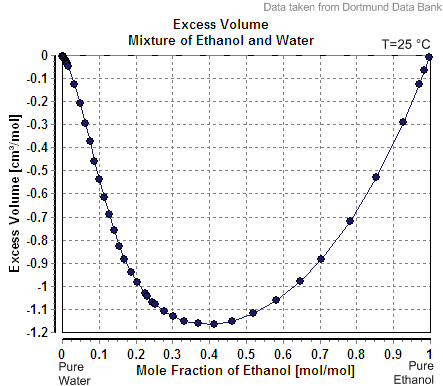
Mole Fraction
In chemistry, the mole fraction or molar fraction, also called mole proportion or molar proportion, is a quantity defined as the ratio between the amount of a constituent substance, ''ni'' (expressed in unit of moles, symbol mol), and the total amount of all constituents in a mixture, ''n''tot (also expressed in moles): :x_i = \frac It is denoted ''xi'' (lowercase Roman letter '' x''), sometimes (lowercase Greek letter chi). (For mixtures of gases, the letter ''y'' is recommended.) It is a dimensionless quantity with dimension of \mathsf/\mathsf and dimensionless unit of moles per mole (mol/mol or molmol−1) or simply 1; metric prefixes may also be used (e.g., nmol/mol for 10−9). When expressed in percent, it is known as the mole percent or molar percentage (unit symbol %, sometimes "mol%", equivalent to cmol/mol for 10−2). The mole fraction is called amount fraction by the International Union of Pure and Applied Chemistry (IUPAC) and amount-of-substance fractio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ratio 4:3). Similarly, the ratio of lemons to oranges is 6:8 (or 3:4) and the ratio of oranges to the total amount of fruit is 8:14 (or 4:7). The numbers in a ratio may be quantities of any kind, such as counts of people or objects, or such as measurements of lengths, weights, time, etc. In most contexts, both numbers are restricted to be Positive integer, positive. A ratio may be specified either by giving both constituting numbers, written as "''a'' to ''b''" or "''a'':''b''", or by giving just the value of their quotient Equal quotients correspond to equal ratios. A statement expressing the equality of two ratios is called a ''proportion''. Consequently, a ratio may be considered as an ordered pair of numbers, a Fraction (mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude (mathematics), magnitude or Physical quantity, quantity of these types of geometric figures and in this context an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system theory, system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Factor
The Lorentz factor or Lorentz term (also known as the gamma factor) is a dimensionless quantity expressing how much the measurements of time, length, and other physical properties change for an object while it moves. The expression appears in several equations in special relativity, and it arises in derivations of the Lorentz transformations. The name originates from its earlier appearance in Lorentz ether theory, Lorentzian electrodynamics – named after the Netherlands, Dutch physicist Hendrik Lorentz. It is generally denoted (the Greek lowercase letter gamma). Sometimes (especially in discussion of superluminal motion) the factor is written as (Greek uppercase-gamma) rather than . Definition The Lorentz factor is defined as \gamma = \frac = \frac = \frac , where: * is the relative velocity between inertial reference frames, * is the speed of light in vacuum, * is the ratio of to , * is coordinate time, * is the proper time for an observer (measuring time intervals in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity, "On the Electrodynamics of Moving Bodies", the theory is presented as being based on just Postulates of special relativity, two postulates: # The laws of physics are Invariant (physics), invariant (identical) in all Inertial frame of reference, inertial frames of reference (that is, Frame of reference, frames of reference with no acceleration). This is known as the principle of relativity. # The speed of light in vacuum is the same for all observers, regardless of the motion of light source or observer. This is known as the principle of light constancy, or the principle of light speed invariance. The first postulate was first formulated by Galileo Galilei (see ''Galilean invariance''). Background Special relativity builds upon important physics ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |