Multidimensional transform on:
[Wikipedia]
[Google]
[Amazon]
In
 where F stands for the z-domain representation of the signal f(n).
A special case of the multidimensional Z transform is the 2D Z transform which is given as
The Fourier transform is a special case of the Z transform evaluated along the
where F stands for the z-domain representation of the signal f(n).
A special case of the multidimensional Z transform is the 2D Z transform which is given as
The Fourier transform is a special case of the Z transform evaluated along the
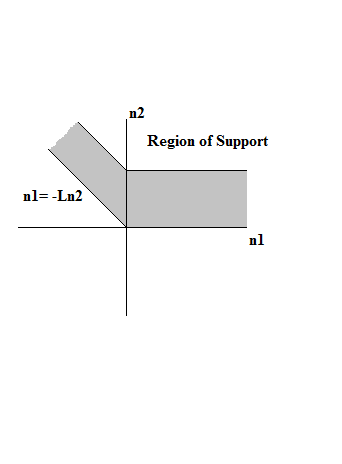
 Points (''z''1,''z''2) for which are located in the ROC.
An example:
If a sequence has a support as shown in Figure 1.1a, then its ROC is shown in Figure 1.1b. This follows that , ''F''(''z''1,''z''2), < ∞ .
lies in the ROC, then all pointsthat satisfy , z1, ≥, z01, and , z2, ≥, z02, lie in the ROC.
Therefore, for figure 1.1a and 1.1b, the ROC would be
:
where ''L'' is the slope.
The 2D Z-transform, similar to the Z-transform, is used in multidimensional signal processing to relate a two-dimensional discrete-time signal to the complex frequency domain in which the 2D surface in 4D space that the Fourier transform lies on is known as the unit surface or unit bicircle.
Points (''z''1,''z''2) for which are located in the ROC.
An example:
If a sequence has a support as shown in Figure 1.1a, then its ROC is shown in Figure 1.1b. This follows that , ''F''(''z''1,''z''2), < ∞ .
lies in the ROC, then all pointsthat satisfy , z1, ≥, z01, and , z2, ≥, z02, lie in the ROC.
Therefore, for figure 1.1a and 1.1b, the ROC would be
:
where ''L'' is the slope.
The 2D Z-transform, similar to the Z-transform, is used in multidimensional signal processing to relate a two-dimensional discrete-time signal to the complex frequency domain in which the 2D surface in 4D space that the Fourier transform lies on is known as the unit surface or unit bicircle.
 The DCT is used in
The DCT is used in
 The inverse multidimensional Laplace transform can be applied to simulate nonlinear circuits. This is done so by formulating a circuit as a state-space and expanding the Inverse Laplace Transform based on Laguerre function expansion.
The Laguerre method can be used to simulate a weakly nonlinear circuit and the Laguerre method can invert a multidimensional Laplace transform efficiently with a high accuracy.
It is observed that a high accuracy and significant speedup can be achieved for simulating large nonlinear circuits using multidimensional Laplace transforms.
The inverse multidimensional Laplace transform can be applied to simulate nonlinear circuits. This is done so by formulating a circuit as a state-space and expanding the Inverse Laplace Transform based on Laguerre function expansion.
The Laguerre method can be used to simulate a weakly nonlinear circuit and the Laguerre method can invert a multidimensional Laplace transform efficiently with a high accuracy.
It is observed that a high accuracy and significant speedup can be achieved for simulating large nonlinear circuits using multidimensional Laplace transforms.
mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series ( ...
and applications, multidimensional transforms are used to analyze the frequency content of signals in a domain of two or more dimensions.
Multidimensional Fourier transform
One of the more popular multidimensional transforms is theFourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
, which converts a signal from a time/space domain representation to a frequency domain representation.Smith, W. Handbook of Real-Time Fast Fourier Transforms:Algorithms to Product Testing, Wiley_IEEE Press, edition 1, pages 73–80, 1995 The discrete-domain multidimensional Fourier transform (FT) can be computed as follows:
:
where ''F'' stands for the multidimensional Fourier transform, ''m'' stands for multidimensional dimension. Define ''f'' as a multidimensional discrete-domain signal. The inverse multidimensional Fourier transform is given by
:
The multidimensional Fourier transform for continuous-domain signals is defined as follows:
:
Properties of Fourier transform
Similar properties of the 1-D FT transform apply, but instead of the input parameter being just a single entry, it's a Multi-dimensional (MD) array or vector. Hence, it's x(n1,…,nM) instead of x(n).Linearity
if , and then, :Shift
if , then
Modulation
Signal modulation is the process of varying one or more properties of a periodic waveform in electronics and telecommunication for the purpose of transmitting information.
The process encodes information in form of the modulation or message ...
if , then
:
Multiplication
if , and then, or,Differentiation
If , then : : :Transposition
If , then :Reflection
If , then :Complex conjugation
If , then :Parseval's theorem (MD)
if , and then, if , then A special case of theParseval's theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum (or integral) of the square of a function is equal to the sum (or integral) of the square of its transform. It originates ...
is when the two multi-dimensional signals are the same. In this case, the theorem portrays the energy conservation of the signal and the term in the summation or integral is the energy-density of the signal.
Separability
A signal or system is said to be separable if it can be expressed as a product of 1-D functions with different independent variables. This phenomenon allows computing the FT transform as a product of 1-D FTs instead of multi-dimensional FT. if , , ... , and if , then , soMD FFT
Afast Fourier transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in ...
(FFT) is an algorithm to compute the discrete Fourier transform (DFT) and its inverse. An FFT computes the DFT and produces exactly the same result as evaluating the DFT definition directly; the only difference is that an FFT is much faster. (In the presence of round-off error
In computing, a roundoff error, also called rounding error, is the difference between the result produced by a given algorithm using exact arithmetic and the result produced by the same algorithm using finite-precision, rounded arithmetic. Roun ...
, many FFT algorithms are also much more accurate than evaluating the DFT definition directly).There are many different FFT algorithms involving a wide range of mathematics, from simple complex-number arithmetic to group theory and number theory. See more in FFT.
MD DFT
The multidimensionaldiscrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discre ...
(DFT) is a sampled version of the discrete-domain FT by evaluating it at sample frequencies that are uniformly spaced. The DFT is given by:
:
for , .
The inverse multidimensional DFT equation is
:
for .
Multidimensional discrete cosine transform
The discrete cosine transform (DCT) is used in a wide range of applications such as datacompression
Compression may refer to:
Physical science
*Compression (physics), size reduction due to forces
*Compression member, a structural element such as a column
*Compressibility, susceptibility to compression
* Gas compression
*Compression ratio, of a ...
, feature extraction
Feature may refer to:
Computing
* Feature recognition, could be a hole, pocket, or notch
* Feature (computer vision), could be an edge, corner or blob
* Feature (machine learning), in statistics: individual measurable properties of the phenome ...
, Image reconstruction, multi-frame detection
{{Unreferenced, date=March 2018
In general, detection is the action of accessing information without specific cooperation from with the sender.
In the history of radio communications, the term "detector" was first used for a device that detected ...
and so on. The multidimensional DCT is given by:
:
for , ''i'' = 1, 2, ..., ''r''.
Multidimensional Laplace transform
The multidimensionalLaplace transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a f ...
is useful for the solution of boundary value problems. Boundary value problems in two or more variables characterized by partial differential equations can be solved by a direct use of the Laplace transform. The Laplace transform for an M-dimensional case is defined as
where F stands for the s-domain representation of the signal f(t).
A special case (along 2 dimensions) of the multi-dimensional Laplace transform of function f(x,y) is defined as
is called the image of and is known as the original of . This special case can be used to solve the Telegrapher's equations
The telegrapher's equations (or telegraph equations) are a set of two coupled, linear partial differential equations that model voltage and current along a linear electrical transmission line. The equations are important because they allow trans ...
.}
Multidimensional Z transform
Source: The multidimensional Z transform is used to map the discrete time domain multidimensional signal to the Z domain. This can be used to check the stability of filters. The equation of the multidimensional Z transform is given by where F stands for the z-domain representation of the signal f(n).
A special case of the multidimensional Z transform is the 2D Z transform which is given as
The Fourier transform is a special case of the Z transform evaluated along the
where F stands for the z-domain representation of the signal f(n).
A special case of the multidimensional Z transform is the 2D Z transform which is given as
The Fourier transform is a special case of the Z transform evaluated along the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
(in 1D) and unit bi-circle (in 2D). i.e. at
where z and w are vectors.
Region of convergence
 Points (''z''1,''z''2) for which are located in the ROC.
An example:
If a sequence has a support as shown in Figure 1.1a, then its ROC is shown in Figure 1.1b. This follows that , ''F''(''z''1,''z''2), < ∞ .
lies in the ROC, then all pointsthat satisfy , z1, ≥, z01, and , z2, ≥, z02, lie in the ROC.
Therefore, for figure 1.1a and 1.1b, the ROC would be
:
where ''L'' is the slope.
The 2D Z-transform, similar to the Z-transform, is used in multidimensional signal processing to relate a two-dimensional discrete-time signal to the complex frequency domain in which the 2D surface in 4D space that the Fourier transform lies on is known as the unit surface or unit bicircle.
Points (''z''1,''z''2) for which are located in the ROC.
An example:
If a sequence has a support as shown in Figure 1.1a, then its ROC is shown in Figure 1.1b. This follows that , ''F''(''z''1,''z''2), < ∞ .
lies in the ROC, then all pointsthat satisfy , z1, ≥, z01, and , z2, ≥, z02, lie in the ROC.
Therefore, for figure 1.1a and 1.1b, the ROC would be
:
where ''L'' is the slope.
The 2D Z-transform, similar to the Z-transform, is used in multidimensional signal processing to relate a two-dimensional discrete-time signal to the complex frequency domain in which the 2D surface in 4D space that the Fourier transform lies on is known as the unit surface or unit bicircle.
Applications
The DCT and DFT are often used in signal processing and image processing, and they are also used to efficiently solve partial differential equations by spectral methods. The DFT can also be used to perform other operations such as convolutions or multiplying large integers. The DFT and DCT have seen wide usage across a large number of fields, we only sketch a few examples below.Image processing
 The DCT is used in
The DCT is used in JPEG
JPEG ( , short for Joint Photographic Experts Group and sometimes retroactively referred to as JPEG 1) is a commonly used method of lossy compression for digital images, particularly for those images produced by digital photography. The degr ...
image compression, MJPEG
Motion JPEG (M-JPEG or MJPEG) is a video compression format in which each video frame or interlaced field of a digital video sequence is compressed separately as a JPEG image.
Originally developed for multimedia PC applications, Motion JPE ...
, MPEG
The Moving Picture Experts Group (MPEG) is an alliance of working groups established jointly by International Organization for Standardization, ISO and International Electrotechnical Commission, IEC that sets standards for media coding, includ ...
, DV, Daala, and Theora
Theora is a free lossy video compression format. It was developed by the Xiph.Org Foundation and distributed without licensing fees alongside their other free and open media projects, including the Vorbis audio format and the Ogg contai ...
video compression
In information theory, data compression, source coding, or bit-rate reduction is the process of encoding information using fewer bits than the original representation. Any particular compression is either lossy or lossless. Lossless compression ...
. There, the two-dimensional DCT-II of ''N''x''N'' blocks are computed and the results are quantized and entropy coded. In this case, ''N'' is typically 8 and the DCT-II formula is applied to each row and column of the block. The result is an 8x8 transform coefficient array in which the: (0,0) element (top-left) is the DC (zero-frequency) component and entries with increasing vertical and horizontal index values represent higher vertical and horizontal spatial frequencies, as shown in the picture on the right.
In image processing, one can also analyze and describe unconventional cryptographic methods based on 2D DCTs, for inserting non-visible binary watermarks into the 2D image plane, and According to different orientations, the 2-D directional DCT-DWT hybrid transform can be applied in denoising ultrasound images. 3-D DCT can also be used to transform video data or 3-D image data in watermark embedding schemes in transform domain.
Spectral analysis
When the DFT is used for spectral analysis, the sequence usually represents a finite set of uniformly spaced time-samples of some signal ''x''(''t'') where ''t'' represents time. The conversion from continuous time to samples (discrete-time) changes the underlyingFourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
of ''x''(''t'') into a discrete-time Fourier transform
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of discrete values.
The DTFT is often used to analyze samples of a continuous function. The term ''discrete-time'' refers ...
(DTFT), which generally entails a type of distortion called aliasing
In signal processing and related disciplines, aliasing is a phenomenon that a reconstructed signal from samples of the original signal contains low frequency components that are not present in the original one. This is caused when, in the ori ...
. Choice of an appropriate sample-rate (see ''Nyquist rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is a value equal to twice the highest frequency ( bandwidth) of a given function or signal. It has units of samples per unit time, conventionally expressed as samples per se ...
'') is the key to minimizing that distortion. Similarly, the conversion from a very long (or infinite) sequence to a manageable size entails a type of distortion called '' leakage'', which is manifested as a loss of detail (aka resolution) in the DTFT. Choice of an appropriate sub-sequence length is the primary key to minimizing that effect. When the available data (and time to process it) is more than the amount needed to attain the desired frequency resolution, a standard technique is to perform multiple DFTs, for example to create a spectrogram
A spectrogram is a visual representation of the spectrum of frequencies of a signal as it varies with time.
When applied to an audio signal, spectrograms are sometimes called sonographs, voiceprints, or voicegrams. When the data are represen ...
. If the desired result is a power spectrum and noise or randomness is present in the data, averaging the magnitude components of the multiple DFTs is a useful procedure to reduce the variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
of the spectrum (also called a periodogram
In signal processing, a periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898. Today, the periodogram is a component of more sophisticated methods (see spectral estimation). It is the most ...
in this context); two examples of such techniques are the Welch method
Welch's method, named after Peter D. Welch, is an approach for spectral density estimation.
It is used in physics, engineering, and applied mathematics for estimating the power of a signal at different frequencies.
The method is based on the c ...
and the Bartlett method; the general subject of estimating the power spectrum of a noisy signal is called spectral estimation.
A final source of distortion (or perhaps ''illusion'') is the DFT itself, because it is just a discrete sampling of the DTFT, which is a function of a continuous frequency domain. That can be mitigated by increasing the resolution of the DFT. That procedure is illustrated at .
*The procedure is sometimes referred to as ''zero-padding'', which is a particular implementation used in conjunction with the fast Fourier transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in ...
(FFT) algorithm. The inefficiency of performing multiplications and additions with zero-valued "samples" is more than offset by the inherent efficiency of the FFT.
*As already noted, leakage imposes a limit on the inherent resolution of the DTFT. So there is a practical limit to the benefit that can be obtained from a fine-grained DFT.
Partial differential equations
Discrete Fourier transforms are often used to solvepartial differential equations
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to how ...
, where again the DFT is used as an approximation for the Fourier series
A Fourier series () is an Series expansion, expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series. By expressing a function as a sum of sines and cosines, many problems ...
(which is recovered in the limit of infinite ''N''). The advantage of this approach is that it expands the signal in complex exponentials ''e''''inx'', which are eigenfunctions of differentiation: ''d''/''dx'' ''e''''inx'' = ''in'' ''e''''inx''. Thus, in the Fourier representation, differentiation is simple—we just multiply by ''i n''. (Note, however, that the choice of ''n'' is not unique due to aliasing; for the method to be convergent, a choice similar to that in the trigonometric interpolation
In mathematics, trigonometric interpolation is interpolation with trigonometric polynomials. Interpolation is the process of finding a function which goes through some given data points. For trigonometric interpolation, this function has to be a ...
section above should be used.) A linear differential equation
In mathematics, a linear differential equation is a differential equation that is linear equation, linear in the unknown function and its derivatives, so it can be written in the form
a_0(x)y + a_1(x)y' + a_2(x)y'' \cdots + a_n(x)y^ = b(x)
wher ...
with constant coefficients is transformed into an easily solvable algebraic equation. One then uses the inverse DFT to transform the result back into the ordinary spatial representation. Such an approach is called a spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain differential equations. The idea is to write the solution of the differential equation as a sum of certain " basis funct ...
.
DCTs are also widely employed in solving partial differential equations by spectral methods, where the different variants of the DCT correspond to slightly different even/odd boundary conditions at the two ends of the array.
Laplace transforms are used to solve partial differential equations. The general theory for obtaining solutions in this technique is developed by theorems on Laplace transform in n dimensions.
The multidimensional Z transform can also be used to solve partial differential equations.
Image processing for arts surface analysis by FFT
One very important factor is that we must apply a non-destructive method to obtain those rare valuables information (from the HVS viewing point, is focused in whole colorimetric and spatial information) about works of art and zero-damage on them. We can understand the arts by looking at a color change or by measuring the surface uniformity change. Since the whole image will be very huge, so we use a double raised cosine window to truncate the image:Angelini, E., Grassin, S.; Piantanida, M.; Corbellini, S.; Ferraris, F.; Neri, A.; Parvis, M. FFT-based imaging processing for cultural heritage monitoring Instrumentation and Measurement Technology Conference (I2MTC), 2010 IEEE : where ''N'' is the image dimension and ''x'', ''y'' are the coordinates from the center of image spans from 0 to ''N''/2. The author wanted to compute an equal value for spatial frequency such as: : where "FFT" denotes the fast Fourier transform, and ''f'' is the spatial frequency spans from 0 to . The proposed FFT-based imaging approach is diagnostic technology to ensure a long life and stable to culture arts. This is a simple, cheap which can be used in museums without affecting their daily use. But this method doesn’t allow a quantitative measure of the corrosion rate.Application to weakly nonlinear circuit simulation
Source:See also
*Discrete cosine transform
A discrete cosine transform (DCT) expresses a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequency, frequencies. The DCT, first proposed by Nasir Ahmed (engineer), Nasir Ahmed in 1972, is a widely ...
* List of Fourier-related transforms
This is a list of linear transformations of function (mathematics), functions related to Fourier analysis. Such transformations Map (mathematics), map a function to a set of coefficients of basis functions, where the basis functions are trigonomet ...
* List of Fourier analysis topics {{Short description, none
This is a list of Fourier analysis topics.
Fourier analysis
* Multiplier (Fourier analysis)
* Fourier shell correlation
* Pinsky phenomenon
Fourier series
* Generalized Fourier series
* Regressive discrete Fourier serie ...
* Multidimensional discrete convolution
In signal processing, multidimensional discrete convolution refers to the mathematical operation between two functions ''f'' and ''g'' on an ''n''-dimensional lattice that produces a third function, also of ''n''-dimensions. Multidimensional discre ...
* 2D Z-transform
* Multidimensional empirical mode decomposition
* Multidimensional signal reconstruction
References
{{Reflist Fourier analysis Integral transforms Multidimensional signal processing