|
Multidimensional Empirical Mode Decomposition
In signal processing, multidimensional empirical mode decomposition (multidimensional EMD) is an extension of the one-dimensional (1-D) EMD algorithm to a signal encompassing multiple dimensions. The Hilbert–Huang empirical mode decomposition (EMD) process decomposes a signal into intrinsic mode functions combined with the Hilbert spectral analysis, known as the Hilbert–Huang transform (HHT). The multidimensional EMD extends the 1-D EMD algorithm into multiple-dimensional signals. This decomposition can be applied to image processing, audio signal processing, and various other multidimensional signals. Motivation Multidimensional empirical mode decomposition is a popular method because of its applications in many fields, such as texture analysis, financial applications, image processing, ocean engineering, seismic research, etc. Recently, several methods of Empirical Mode Decomposition have been used to analyze characterization of multidimensional signals. Introduction to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital re ...
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim Alan Victor Oppenheim''Alan Victor Oppenheim'' was elected in 1987 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Huang Transform
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician, one of the most influential mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory, the calculus of variations, commutative algebra, algebraic number theory, the foundations of geometry, spectral theory of operators and its application to integral equations, mathematical physics, and the foundations of mathematics (particularly proof theory). Hilbert adopted and defended Georg Cantor's set theory and transfinite numbers. In 1900, he presented a collection of problems that set the course for much of the mathematical research of the 20th century. Hilbert and his students contributed significantly to establishing rigor and developed important tools used in modern mathematical physics. Hilbert is known as one of the founders of proof theory and mathematical logic. Life Early life and ed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Difference Approximation
A finite difference is a mathematical expression of the form . If a finite difference is divided by , one gets a difference quotient. The approximation of derivatives by finite differences plays a central role in finite difference methods for the numerical solution of differential equations, especially boundary value problems. The difference operator, commonly denoted \Delta is the operator that maps a function to the function \Delta /math> defined by :\Delta x)= f(x+1)-f(x). A difference equation is a functional equation that involves the finite difference operator in the same way as a differential equation involves derivatives. There are many similarities between difference equations and differential equations, specially in the solving methods. Certain recurrence relations can be written as difference equations by replacing iteration notation with finite differences. In numerical analysis, finite differences are widely used for approximating derivatives, and the term "finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Direction Implicit Method
In numerical linear algebra, the alternating-direction implicit (ADI) method is an iterative method used to solve Sylvester matrix equations. It is a popular method for solving the large matrix equations that arise in systems theory and control, and can be formulated to construct solutions in a memory-efficient, factored form. It is also used to numerically solve parabolic and elliptic partial differential equations, and is a classic method used for modeling heat conduction and solving the diffusion equation in two or more dimensions.. It is an example of an operator splitting method. ADI for matrix equations The method The ADI method is a two step iteration process that alternately updates the column and row spaces of an approximate solution to AX - XB = C. One ADI iteration consists of the following steps:1. Solve for X^, where \left( A - \beta_ I\right) X^ = X^\left( B - \beta_ I \right) + C. 2. Solve for X^, where X^\left( B - \alpha_ I \right) = \left( A - \alpha_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
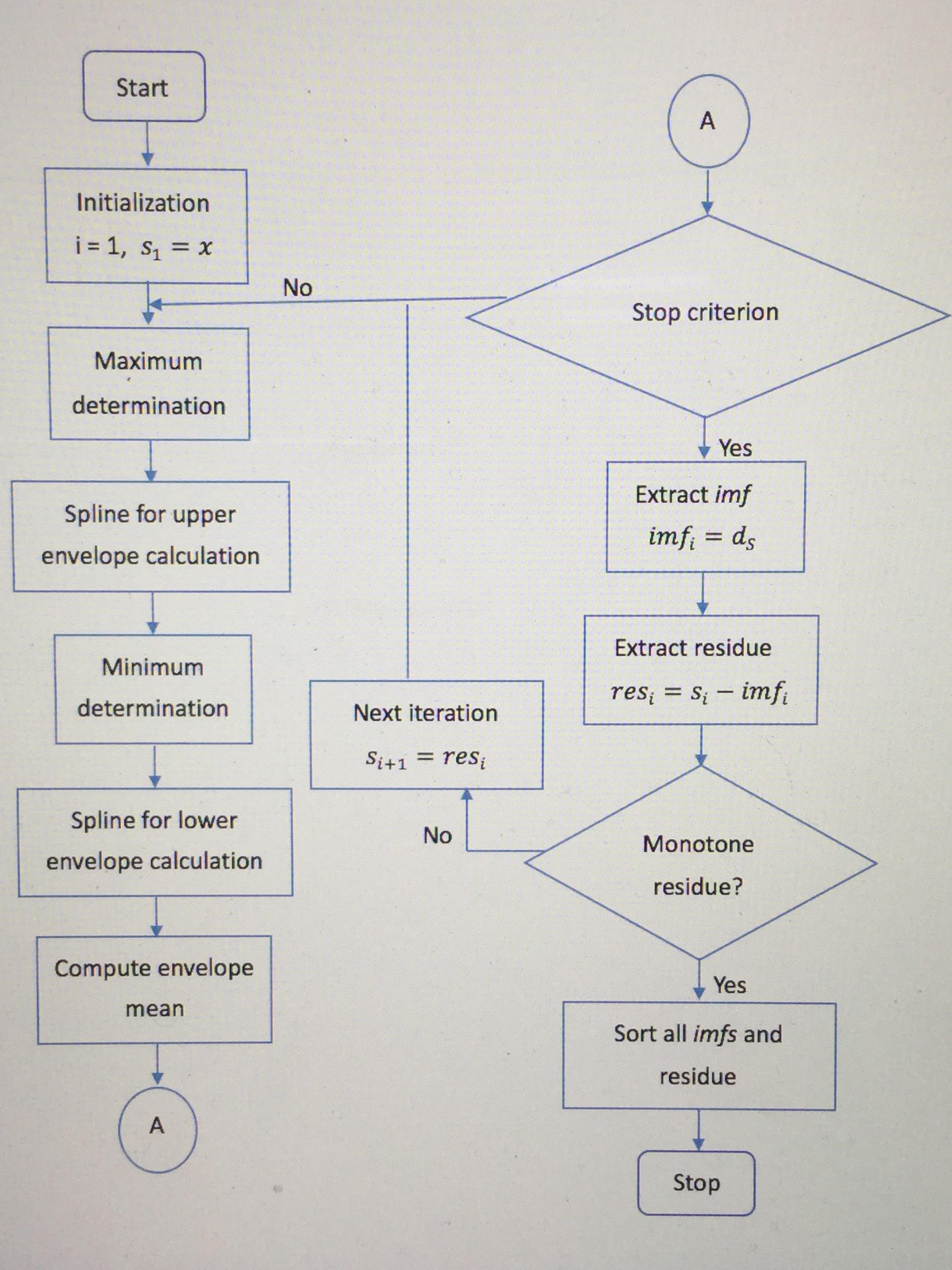
Flow Chart For FABEMD Algorithm
Flow may refer to: Science and technology * Fluid flow, the motion of a gas or liquid * Flow (geomorphology), a type of mass wasting or slope movement in geomorphology * Flow (mathematics), a group action of the real numbers on a set * Flow (psychology), a mental state of being fully immersed and focused * Flow, a spacecraft of NASA's GRAIL program Computing * Flow network, graph-theoretic version of a mathematical flow * Flow analysis * Calligra Flow, free diagramming software * Dataflow, a broad concept in computer systems with many different meanings * Microsoft Flow (renamed to Power Automate in 2019), a workflow toolkit in Microsoft Dynamics * Neos Flow, a free and open source web application framework written in PHP * webMethods Flow, a graphical programming language * FLOW (programming language), an educational programming language from the 1970s * Flow (web browser), a web browser with a proprietary rendering engine Arts, entertainment and media * ''Flow'' (journal), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample BEMD Simulation Results For A Noisy Signal With Imf
Sample or samples may refer to: Base meaning * Sample (statistics), a subset of a population – complete data set * Sample (signal), a digital discrete sample of a continuous analog signal * Sample (material), a specimen or small quantity of something * Sample (graphics), an intersection of a color channel and a pixel * SAMPLE history, a mnemonic acronym for questions medical first responders should ask * Product sample, a sample of a consumer product that is given to the consumer so that he or she may try a product before committing to a purchase * Standard cross-cultural sample, a sample of 186 cultures, used by scholars engaged in cross-cultural studies People * Sample (surname) * Samples (surname) * Junior Samples (1926–1983), American comedian Places * Sample, Kentucky, unincorporated community, United States * Sampleville, Ohio, unincorporated community, United States * Hugh W. and Sarah Sample House, listed on the National Register of Historic Places in Iowa, United ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Orthogonal Function
In statistics and signal processing, the method of empirical orthogonal function (EOF) analysis is a decomposition of a signal or data set in terms of orthogonal basis functions which are determined from the data. The term is also interchangeable with the geographically weighted Principal components analysis in geophysics. The ''i'' th basis function is chosen to be orthogonal to the basis functions from the first through ''i'' − 1, and to minimize the residual variance. That is, the basis functions are chosen to be different from each other, and to account for as much variance as possible. The method of EOF analysis is similar in spirit to harmonic analysis, but harmonic analysis typically uses predetermined orthogonal functions, for example, sine and cosine functions at fixed frequencies. In some cases the two methods may yield essentially the same results. The basis functions are typically found by computing the eigenvectors of the covariance matrix of the data se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Orthogonal Functions
In statistics and signal processing, the method of empirical orthogonal function (EOF) analysis is a decomposition of a signal or data set in terms of orthogonal basis functions which are determined from the data. The term is also interchangeable with the geographically weighted Principal components analysis in geophysics. The ''i'' th basis function is chosen to be orthogonal to the basis functions from the first through ''i'' − 1, and to minimize the residual variance. That is, the basis functions are chosen to be different from each other, and to account for as much variance as possible. The method of EOF analysis is similar in spirit to harmonic analysis, but harmonic analysis typically uses predetermined orthogonal functions, for example, sine and cosine functions at fixed frequencies. In some cases the two methods may yield essentially the same results. The basis functions are typically found by computing the eigenvectors of the covariance matrix of the data set. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Component Analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and enabling the visualization of multidimensional data. Formally, PCA is a statistical technique for reducing the dimensionality of a dataset. This is accomplished by linearly transforming the data into a new coordinate system where (most of) the variation in the data can be described with fewer dimensions than the initial data. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identify clusters of closely related data points. Principal component analysis has applications in many fields such as population genetics, microbiome studies, and atmospheric science. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyadic Transformation
The dyadic transformation (also known as the dyadic map, bit shift map, 2''x'' mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping (i.e., recurrence relation) : T: , 1) \to [0, 1)^\infty : x \mapsto (x_0, x_1, x_2, \ldots) (where [0, 1)^\infty is the set of sequences from [0, 1)) produced by the rule : x_0 = x : \text n \ge 0,\ x_ = (2 x_n) \bmod 1. Equivalently, the dyadic transformation can also be defined as the iterated function map of the piecewise linear function : T(x)=\begin2x & 0 \le x < \frac \\2x-1 & \frac \le x < 1. \end The name ''bit shift map'' arises because, if the value of an iterate is written in notation, the next iterate is obtained by shifting the binary point one bit to the right, and if the bit to the left of the new binary point is a "one", replacing it with a zero. The dyadic transfo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |