Mathematical morphology on:
[Wikipedia]
[Google]
[Amazon]
 Mathematical morphology (MM) is a theory and technique for the analysis and processing of
Mathematical morphology (MM) is a theory and technique for the analysis and processing of
 The
The
 The
The
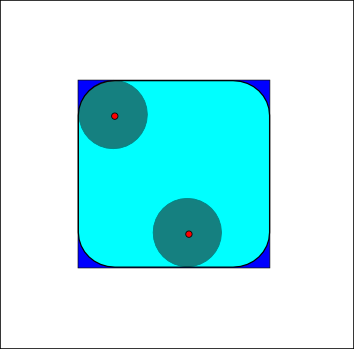 The opening of ''A'' by ''B'' is obtained by the erosion of ''A'' by ''B'', followed by dilation of the resulting image by ''B'':
:
The opening is also given by , which means that it is the locus of translations of the structuring element ''B'' inside the image ''A''. In the case of the square of side 10, and a disc of radius 2 as the structuring element, the opening is a square of side 10 with rounded corners, where the corner radius is 2.
Example application: Let's assume someone has written a note on a non-soaking paper and that the writing looks as if it is growing tiny hairy roots all over. Opening essentially removes the outer tiny "hairline" leaks and restores the text. The side effect is that it rounds off things. The sharp edges start to disappear.
The opening of ''A'' by ''B'' is obtained by the erosion of ''A'' by ''B'', followed by dilation of the resulting image by ''B'':
:
The opening is also given by , which means that it is the locus of translations of the structuring element ''B'' inside the image ''A''. In the case of the square of side 10, and a disc of radius 2 as the structuring element, the opening is a square of side 10 with rounded corners, where the corner radius is 2.
Example application: Let's assume someone has written a note on a non-soaking paper and that the writing looks as if it is growing tiny hairy roots all over. Opening essentially removes the outer tiny "hairline" leaks and restores the text. The side effect is that it rounds off things. The sharp edges start to disappear.
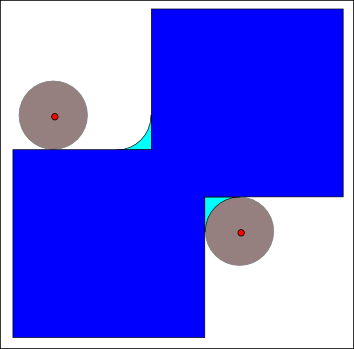 The closing of ''A'' by ''B'' is obtained by the dilation of ''A'' by ''B'', followed by erosion of the resulting structure by ''B'':
:
The closing can also be obtained by , where ''X''''c'' denotes the
The closing of ''A'' by ''B'' is obtained by the dilation of ''A'' by ''B'', followed by erosion of the resulting structure by ''B'':
:
The closing can also be obtained by , where ''X''''c'' denotes the
 In
In
''Implementing continuous-scale morphology via curve evolution''
Pattern Recognition, 26(9):1363–1372, 1993.
Online course on mathematical morphology
by Jean Serra (in English, French, and Spanish)
Center of Mathematical Morphology
Paris School of Mines
History of Mathematical Morphology
by Georges Matheron and Jean Serra
Morphology Digest, a newsletter on mathematical morphology
by Pierre Soille
Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lectures 16-18 are on Mathematical Morphology
by Alan Peters
by Robyn Owens
SMIL - A Simple (but efficient) Morphological Image Library (from Ecole des Mines de Paris)
Free SIMD Optimized Image processing library
FILTERS : a free open source image processing library
* ttp://www.johanneshjorth.se/SynD Morphological analysis of neurons using Matlab Digital geometry Image processing
 Mathematical morphology (MM) is a theory and technique for the analysis and processing of
Mathematical morphology (MM) is a theory and technique for the analysis and processing of geometrical
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
structures, based on set theory
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concern ...
, lattice theory
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bou ...
, topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ...
, and random function
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that app ...
s. MM is most commonly applied to digital image
A digital image is an image composed of picture elements, also known as ''pixels'', each with '' finite'', '' discrete quantities'' of numeric representation for its intensity or gray level that is an output from its two-dimensional functions ...
s, but it can be employed as well on graphs, surface meshes, solids, and many other spatial structures.
Topological and geometrical
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous g ...
-space concepts such as size, shape
A shape or figure is a graphical representation of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type.
A plane shape or plane figure is constrained to lie ...
, convexity
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytope ...
, connectivity, and geodesic distance, were introduced by MM on both continuous and discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points form a , meaning they are ''isolated'' from each other in a certain sense. The discrete topology is the finest top ...
s. MM is also the foundation of morphological image processing
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensio ...
, which consists of a set of operators that transform images according to the above characterizations.
The basic morphological operators are erosion
Erosion is the action of surface processes (such as water flow or wind) that removes soil, rock, or dissolved material from one location on the Earth's crust, and then transports it to another location where it is deposited. Erosion is d ...
, dilation
Dilation (or dilatation) may refer to:
Physiology or medicine
* Cervical dilation, the widening of the cervix in childbirth, miscarriage etc.
* Coronary dilation, or coronary reflex
* Dilation and curettage, the opening of the cervix and surgi ...
, opening and closing.
MM was originally developed for binary image
A binary image is one that consists of pixels that can have one of exactly two colors, usually black and white. Binary images are also called ''bi-level'' or ''two-level'', Pixelart made of two colours is often referred to as ''1-Bit'' or ''1b ...
s, and was later extended to grayscale
In digital photography, computer-generated imagery, and colorimetry, a grayscale image is one in which the value of each pixel is a single sample representing only an ''amount'' of light; that is, it carries only intensity information. Graysc ...
functions and images. The subsequent generalization to complete lattice
In mathematics, a complete lattice is a partially ordered set in which ''all'' subsets have both a supremum (join) and an infimum (meet). A lattice which satisfies at least one of these properties is known as a ''conditionally complete lattice.'' ...
s is widely accepted today as MM's theoretical foundation.
History
Mathematical Morphology was developed in 1964 by the collaborative work ofGeorges Matheron
Georges François Paul Marie Matheron (2 December 1930 – 7 August 2000) was a French mathematician and civil engineer of mines, known as the founder of geostatistics and a co-founder (together with Jean Serra) of mathematical morphology. In 196 ...
and Jean Serra, at the ''École des Mines de Paris
Mines Paris - PSL, officially École nationale supérieure des mines de Paris (until May 2022 Mines ParisTech, also known as École des mines de Paris, ENSMP, Mines de Paris, les Mines, or Paris School of Mines), is a French grande école and a ...
'', France
France (), officially the French Republic ( ), is a country primarily located in Western Europe. It also comprises of Overseas France, overseas regions and territories in the Americas and the Atlantic Ocean, Atlantic, Pacific Ocean, Pac ...
. Matheron supervised the PhD PHD or PhD may refer to:
* Doctor of Philosophy (PhD), an academic qualification
Entertainment
* '' PhD: Phantasy Degree'', a Korean comic series
* '' Piled Higher and Deeper'', a web comic
* Ph.D. (band), a 1980s British group
** Ph.D. (Ph.D. al ...
thesis
A thesis ( : theses), or dissertation (abbreviated diss.), is a document submitted in support of candidature for an academic degree or professional qualification presenting the author's research and findings.International Standard ISO 7144 ...
of Serra, devoted to the quantification of mineral characteristics from thin cross sections, and this work resulted in a novel practical approach, as well as theoretical advancements in integral geometry and topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ...
.
In 1968, the ''Centre de Morphologie Mathématique
''Centre de Morphologie Mathématique'' (or Center of Mathematical Morphology, or CMM) is a research center of the ''École des Mines de Paris'', France, devoted to the research and promotion of mathematical morphology. It was created in 1968 as a ...
'' was founded by the École des Mines de Paris in Fontainebleau
Fontainebleau (; ) is a commune in the metropolitan area of Paris, France. It is located south-southeast of the centre of Paris. Fontainebleau is a sub-prefecture of the Seine-et-Marne department, and it is the seat of the ''arrondissemen ...
, France, led by Matheron and Serra.
During the rest of the 1960s and most of the 1970s, MM dealt essentially with binary image
A binary image is one that consists of pixels that can have one of exactly two colors, usually black and white. Binary images are also called ''bi-level'' or ''two-level'', Pixelart made of two colours is often referred to as ''1-Bit'' or ''1b ...
s, treated as sets, and generated a large number of binary operator
In mathematics, a binary operation or dyadic operation is a rule for combining two elements (called operands) to produce another element. More formally, a binary operation is an operation of arity two.
More specifically, an internal binary o ...
s and techniques: Hit-or-miss transform
In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration (or pattern) in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements. The result of the hit-or-m ...
, dilation
Dilation (or dilatation) may refer to:
Physiology or medicine
* Cervical dilation, the widening of the cervix in childbirth, miscarriage etc.
* Coronary dilation, or coronary reflex
* Dilation and curettage, the opening of the cervix and surgi ...
, erosion
Erosion is the action of surface processes (such as water flow or wind) that removes soil, rock, or dissolved material from one location on the Earth's crust, and then transports it to another location where it is deposited. Erosion is d ...
, opening, closing, granulometry, thinning
Thinning is a term used in agricultural sciences to mean the removal of some plants, or parts of plants, to make room for the growth of others. Selective removal of parts of a plant such as branches, buds, or roots is typically known as pruning. ...
, skeletonization, ultimate erosion, conditional bisector, and others. A random approach was also developed, based on novel image models. Most of the work in that period was developed in Fontainebleau.
From the mid-1970s to mid-1980s, MM was generalized to grayscale
In digital photography, computer-generated imagery, and colorimetry, a grayscale image is one in which the value of each pixel is a single sample representing only an ''amount'' of light; that is, it carries only intensity information. Graysc ...
functions and image
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensio ...
s as well. Besides extending the main concepts (such as dilation, erosion, etc.) to functions, this generalization yielded new operators, such as morphological gradients, top-hat transform and the Watershed
Watershed is a hydrological term, which has been adopted in other fields in a more or less figurative sense. It may refer to:
Hydrology
* Drainage divide, the line that separates neighbouring drainage basins
* Drainage basin, called a "watershe ...
(MM's main segmentation approach).
In the 1980s and 1990s, MM gained a wider recognition, as research centers in several countries began to adopt and investigate the method. MM started to be applied to a large number of imaging problems and applications, especially in the field of non-linear filtering of noisy images.
In 1986, Serra further generalized MM, this time to a theoretical framework based on complete lattice
In mathematics, a complete lattice is a partially ordered set in which ''all'' subsets have both a supremum (join) and an infimum (meet). A lattice which satisfies at least one of these properties is known as a ''conditionally complete lattice.'' ...
s. This generalization brought flexibility to the theory, enabling its application to a much larger number of structures, including color images, video, graphs, mesh
A mesh is a barrier made of connected strands of metal, fiber, or other flexible or ductile materials. A mesh is similar to a web or a net in that it has many attached or woven strands.
Types
* A plastic mesh may be extruded, oriented, exp ...
es, etc. At the same time, Matheron and Serra also formulated a theory for morphological filtering
Filter, filtering or filters may refer to:
Science and technology
Computing
* Filter (higher-order function), in functional programming
* Filter (software), a computer program to process a data stream
* Filter (video), a software component tha ...
, based on the new lattice framework.
The 1990s and 2000s also saw further theoretical advancements, including the concepts of '' connections'' and '' levelings''.
In 1993, the first International Symposium on Mathematical Morphology (ISMM) took place in Barcelona
Barcelona ( , , ) is a city on the coast of northeastern Spain. It is the capital and largest city of the autonomous community of Catalonia, as well as the second most populous municipality of Spain. With a population of 1.6 million within c ...
, Spain
, image_flag = Bandera de España.svg
, image_coat = Escudo de España (mazonado).svg
, national_motto = '' Plus ultra'' (Latin)(English: "Further Beyond")
, national_anthem = (English: "Royal March")
, ...
. Since then, ISMMs are organized every 2–3 years: Fontainebleau
Fontainebleau (; ) is a commune in the metropolitan area of Paris, France. It is located south-southeast of the centre of Paris. Fontainebleau is a sub-prefecture of the Seine-et-Marne department, and it is the seat of the ''arrondissemen ...
, France
France (), officially the French Republic ( ), is a country primarily located in Western Europe. It also comprises of Overseas France, overseas regions and territories in the Americas and the Atlantic Ocean, Atlantic, Pacific Ocean, Pac ...
(1994); Atlanta
Atlanta ( ) is the capital and most populous city of the U.S. state of Georgia. It is the seat of Fulton County, the most populous county in Georgia, but its territory falls in both Fulton and DeKalb counties. With a population of 498,7 ...
, USA (1996); Amsterdam
Amsterdam ( , , , lit. ''The Dam on the River Amstel'') is the capital and most populous city of the Netherlands, with The Hague being the seat of government. It has a population of 907,976 within the city proper, 1,558,755 in the urban ar ...
, Netherlands
)
, anthem = ( en, "William of Nassau")
, image_map =
, map_caption =
, subdivision_type = Sovereign state
, subdivision_name = Kingdom of the Netherlands
, established_title = Before independence
, established_date = Spanish Netherl ...
(1998); Palo Alto
Palo Alto (; Spanish for "tall stick") is a charter city in the northwestern corner of Santa Clara County, California, United States, in the San Francisco Bay Area, named after a coastal redwood tree known as El Palo Alto.
The city was es ...
, CA, USA (2000); Sydney
Sydney ( ) is the capital city of the state of New South Wales, and the most populous city in both Australia and Oceania. Located on Australia's east coast, the metropolis surrounds Sydney Harbour and extends about towards the Blue Mounta ...
, Australia
Australia, officially the Commonwealth of Australia, is a sovereign country comprising the mainland of the Australian continent, the island of Tasmania, and numerous smaller islands. With an area of , Australia is the largest country by ...
(2002); Paris
Paris () is the capital and most populous city of France, with an estimated population of 2,165,423 residents in 2019 in an area of more than 105 km² (41 sq mi), making it the 30th most densely populated city in the world in 2020. Si ...
, France
France (), officially the French Republic ( ), is a country primarily located in Western Europe. It also comprises of Overseas France, overseas regions and territories in the Americas and the Atlantic Ocean, Atlantic, Pacific Ocean, Pac ...
(2005); Rio de Janeiro
Rio de Janeiro ( , , ; literally 'River of January'), or simply Rio, is the capital of the state of the same name, Brazil's third-most populous state, and the second-most populous city in Brazil, after São Paulo. Listed by the GaWC as a b ...
, Brazil
Brazil ( pt, Brasil; ), officially the Federative Republic of Brazil (Portuguese: ), is the largest country in both South America and Latin America. At and with over 217 million people, Brazil is the world's fifth-largest country by area ...
(2007); Groningen
Groningen (; gos, Grunn or ) is the capital city and main municipality of Groningen (province), Groningen province in the Netherlands. The ''capital of the north'', Groningen is the largest place as well as the economic and cultural centre of t ...
, Netherlands
)
, anthem = ( en, "William of Nassau")
, image_map =
, map_caption =
, subdivision_type = Sovereign state
, subdivision_name = Kingdom of the Netherlands
, established_title = Before independence
, established_date = Spanish Netherl ...
(2009); Intra (Verbania
Verbania (, , ) is the most populous ''comune'' (municipality) and the capital city of the province of Verbano-Cusio-Ossola in the Piedmont region of northwest Italy. It is situated on the shore of Lake Maggiore, about north-west of Milan and ...
), Italy
Italy ( it, Italia ), officially the Italian Republic, ) or the Republic of Italy, is a country in Southern Europe. It is located in the middle of the Mediterranean Sea, and its territory largely coincides with the homonymous geographical ...
(2011); Uppsala
Uppsala (, or all ending in , ; archaically spelled ''Upsala'') is the county seat of Uppsala County and the fourth-largest city in Sweden, after Stockholm, Gothenburg, and Malmö. It had 177,074 inhabitants in 2019.
Located north of the ca ...
, Sweden (2013); Reykjavík
Reykjavík ( ; ) is the capital and largest city of Iceland. It is located in southwestern Iceland, on the southern shore of Faxaflói bay. Its latitude is 64°08' N, making it the world's northernmost capital of a sovereign state. With a po ...
, Iceland (2015); and Fontainebleau
Fontainebleau (; ) is a commune in the metropolitan area of Paris, France. It is located south-southeast of the centre of Paris. Fontainebleau is a sub-prefecture of the Seine-et-Marne department, and it is the seat of the ''arrondissemen ...
, France
France (), officially the French Republic ( ), is a country primarily located in Western Europe. It also comprises of Overseas France, overseas regions and territories in the Americas and the Atlantic Ocean, Atlantic, Pacific Ocean, Pac ...
(2017).
References
* "Introduction" by Pierre Soille, in ( Serra ''et al.'' (Eds.) 1994), pgs. 1-4. * "Appendix A: The 'Centre de Morphologie Mathématique', an overview" by Jean Serra, in ( Serra ''et al.'' (Eds.) 1994), pgs. 369-374. *"Foreword" in ( Ronse ''et al.'' (Eds.) 2005)Binary morphology
In binary morphology, an image is viewed as asubset
In mathematics, set ''A'' is a subset of a set ''B'' if all elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ...
of a Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidea ...
or the integer grid , for some dimension ''d''.
Structuring element
The basic idea in binary morphology is to probe an image with a simple, pre-defined shape, drawing conclusions on how this shape fits or misses the shapes in the image. This simple "probe" is called thestructuring element In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image. It is typically used in morphological oper ...
, and is itself a binary image (i.e., a subset of the space or grid).
Here are some examples of widely used structuring elements (denoted by ''B''):
* Let ; ''B'' is an open disk of radius ''r'', centered at the origin.
* Let ; ''B'' is a 3 × 3 square, that is, ''B'' = .
* Let ; ''B'' is the "cross" given by ''B'' = .
Basic operators
The basic operations are shift-invariant (translation invariant
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by .
In physics and mathematics, continuous translational symmetry is the invariance of a system of equa ...
) operators strongly related to Minkowski addition
In geometry, the Minkowski sum (also known as dilation) of two sets of position vectors ''A'' and ''B'' in Euclidean space is formed by adding each vector in ''A'' to each vector in ''B'', i.e., the set
: A + B = \.
Analogously, the Minkowsk ...
.
Let ''E'' be a Euclidean space or an integer grid, and ''A'' a binary image in ''E''.
Erosion
 The
The erosion
Erosion is the action of surface processes (such as water flow or wind) that removes soil, rock, or dissolved material from one location on the Earth's crust, and then transports it to another location where it is deposited. Erosion is d ...
of the binary image ''A'' by the structuring element ''B'' is defined by
:
where ''B''''z'' is the translation of ''B'' by the vector ''z'', i.e., , .
When the structuring element ''B'' has a center (e.g., ''B'' is a disk or a square), and this center is located on the origin of ''E'', then the erosion of ''A'' by ''B'' can be understood as the locus of points reached by the center of ''B'' when ''B'' moves inside ''A''. For example, the erosion of a square of side 10, centered at the origin, by a disc of radius 2, also centered at the origin, is a square of side 6 centered at the origin.
The erosion of ''A'' by ''B'' is also given by the expression .
Example application: Assume we have received a fax of a dark photocopy. Everything looks like it was written with a pen that is bleeding. Erosion process will allow thicker lines to get skinny and detect the hole inside the letter "o".
Dilation
 The
The dilation
Dilation (or dilatation) may refer to:
Physiology or medicine
* Cervical dilation, the widening of the cervix in childbirth, miscarriage etc.
* Coronary dilation, or coronary reflex
* Dilation and curettage, the opening of the cervix and surgi ...
of ''A'' by the structuring element ''B'' is defined by
:
The dilation is commutative, also given by .
If ''B'' has a center on the origin, as before, then the dilation of ''A'' by ''B'' can be understood as the locus of the points covered by ''B'' when the center of ''B'' moves inside ''A''. In the above example, the dilation of the square of side 10 by the disk of radius 2 is a square of side 14, with rounded corners, centered at the origin. The radius of the rounded corners is 2.
The dilation can also be obtained by , where ''B''''s'' denotes the symmetric of ''B'', that is, .
Example application: dilation is the dual operation of the erosion. Figures that are very lightly drawn get thick when "dilated". Easiest way to describe it is to imagine the same fax/text is written with a thicker pen.
Opening
 The opening of ''A'' by ''B'' is obtained by the erosion of ''A'' by ''B'', followed by dilation of the resulting image by ''B'':
:
The opening is also given by , which means that it is the locus of translations of the structuring element ''B'' inside the image ''A''. In the case of the square of side 10, and a disc of radius 2 as the structuring element, the opening is a square of side 10 with rounded corners, where the corner radius is 2.
Example application: Let's assume someone has written a note on a non-soaking paper and that the writing looks as if it is growing tiny hairy roots all over. Opening essentially removes the outer tiny "hairline" leaks and restores the text. The side effect is that it rounds off things. The sharp edges start to disappear.
The opening of ''A'' by ''B'' is obtained by the erosion of ''A'' by ''B'', followed by dilation of the resulting image by ''B'':
:
The opening is also given by , which means that it is the locus of translations of the structuring element ''B'' inside the image ''A''. In the case of the square of side 10, and a disc of radius 2 as the structuring element, the opening is a square of side 10 with rounded corners, where the corner radius is 2.
Example application: Let's assume someone has written a note on a non-soaking paper and that the writing looks as if it is growing tiny hairy roots all over. Opening essentially removes the outer tiny "hairline" leaks and restores the text. The side effect is that it rounds off things. The sharp edges start to disappear.
Closing
 The closing of ''A'' by ''B'' is obtained by the dilation of ''A'' by ''B'', followed by erosion of the resulting structure by ''B'':
:
The closing can also be obtained by , where ''X''''c'' denotes the
The closing of ''A'' by ''B'' is obtained by the dilation of ''A'' by ''B'', followed by erosion of the resulting structure by ''B'':
:
The closing can also be obtained by , where ''X''''c'' denotes the complement
A complement is something that completes something else.
Complement may refer specifically to:
The arts
* Complement (music), an interval that, when added to another, spans an octave
** Aggregate complementation, the separation of pitch-clas ...
of ''X'' relative to ''E'' (that is, ). The above means that the closing is the complement of the locus of translations of the symmetric of the structuring element outside the image ''A''.
Properties of the basic operators
Here are some properties of the basic binary morphological operators (dilation, erosion, opening and closing): * They aretranslation invariant
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by .
In physics and mathematics, continuous translational symmetry is the invariance of a system of equa ...
.
* They are increasing, that is, if , then , and , etc.
* The dilation is commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of ...
: .
* If the origin of ''E'' belongs to the structuring element ''B'', then .
* The dilation is associative
In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement ...
, i.e., . Moreover, the erosion satisfies .
* Erosion and dilation satisfy the duality .
* Opening and closing satisfy the duality .
* The dilation is distributive over set union
In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other.
A refers to a union of ze ...
* The erosion is distributive over set intersection
* The dilation is a pseudo-inverse of the erosion, and vice versa, in the following sense: if and only if .
* Opening and closing are idempotent
Idempotence (, ) is the property of certain operations in mathematics and computer science whereby they can be applied multiple times without changing the result beyond the initial application. The concept of idempotence arises in a number of pl ...
.
* Opening is anti-extensive, i.e., , whereas the closing is ''extensive'', i.e., .
Other operators and tools
*Hit-or-miss transform
In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration (or pattern) in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements. The result of the hit-or-m ...
* Pruning transform
* Morphological skeleton
* Filtering by reconstruction
* Ultimate erosions and conditional bisectors
* Granulometry
* Geodesic distance functions
Grayscale morphology
 In
In grayscale
In digital photography, computer-generated imagery, and colorimetry, a grayscale image is one in which the value of each pixel is a single sample representing only an ''amount'' of light; that is, it carries only intensity information. Graysc ...
morphology, images are functions mapping a Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidea ...
or grid ''E'' into , where is the set of reals, is an element larger than any real number, and is an element smaller than any real number.
Grayscale structuring elements are also functions of the same format, called "structuring functions".
Denoting an image by ''f''(''x'') the structuring function by ''b''(''x'') and the support of ''g'' by ''B'', the grayscale dilation of ''f'' by ''b'' is given by
:
where "sup" denotes the supremum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest ...
.
Similarly, the erosion of ''f'' by ''b'' is given by
:
where "inf" denotes the infimum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest lo ...
.
Just like in binary morphology, the opening and closing are given respectively by
:
:
Flat structuring functions
It is common to use flat structuring elements in morphological applications. Flat structuring functions are functions ''b''(''x'') in the form : where . In this case, the dilation and erosion are greatly simplified, and given respectively by : : In the bounded, discrete case (''E'' is a grid and ''B'' is bounded), thesupremum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest ...
and infimum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest lo ...
operators can be replaced by the maximum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given r ...
and minimum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given r ...
. Thus, dilation and erosion are particular cases of order statistics
In statistics, the ''k''th order statistic of a statistical sample is equal to its ''k''th-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference.
Importa ...
filters, with dilation returning the maximum value within a moving window (the symmetric of the structuring function support ''B''), and the erosion returning the minimum value within the moving window ''B''.
In the case of flat structuring element, the morphological operators depend only on the relative ordering of pixel
In digital imaging, a pixel (abbreviated px), pel, or picture element is the smallest addressable element in a raster image, or the smallest point in an all points addressable display device.
In most digital display devices, pixels are the ...
values, regardless their numerical values, and therefore are especially suited to the processing of binary images and grayscale images whose light transfer function is not known.
Other operators and tools
* Morphological gradients * Top-hat transform * Watershed algorithm By combining these operators one can obtain algorithms for many image processing tasks, such as feature detection, image segmentation,image sharpening
Image editing encompasses the processes of altering images, whether they are digital photographs, traditional photo-chemical photographs, or illustrations. Traditional analog image editing is known as photo retouching, using tools such as ...
, image filtering, and classification Classification is a process related to categorization, the process in which ideas and objects are recognized, differentiated and understood.
Classification is the grouping of related facts into classes.
It may also refer to:
Business, organizat ...
.
Along this line one should also look into Continuous MorphologyG. Sapiro, R. Kimmel, D. Shaked, B. Kimia, and A. M. Bruckstein.''Implementing continuous-scale morphology via curve evolution''
Pattern Recognition, 26(9):1363–1372, 1993.
Mathematical morphology on complete lattices
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which ''all'' subsets have both a supremum (join) and an infimum (meet). A lattice which satisfies at least one of these properties is known as a ''conditionally complete lattice.'' ...
s are partially ordered set
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary ...
s, where every subset has an infimum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest lo ...
and a supremum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest ...
. In particular, it contains a least element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set (poset) is an element of S that is greater than every other element of S. The term least element is defined dually, that is, it is an elem ...
and a greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set (poset) is an element of S that is greater than every other element of S. The term least element is defined dually, that is, it is an elem ...
(also denoted "universe").
Adjunctions (dilation and erosion)
Let be a complete lattice, with infimum and supremum symbolized by and , respectively. Its universe and least element are symbolized by ''U'' and , respectively. Moreover, let be a collection of elements from ''L''. A dilation is any operator that distributes over the supremum, and preserves the least element. I.e.: * , * . An erosion is any operator that distributes over the infimum, and preserves the universe. I.e.: * , * . Dilations and erosions formGalois connection In mathematics, especially in order theory, a Galois connection is a particular correspondence (typically) between two partially ordered sets (posets). Galois connections find applications in various mathematical theories. They generalize the funda ...
s. That is, for every dilation there is one and only one erosion that satisfies
:
for all .
Similarly, for every erosion there is one and only one dilation satisfying the above connection.
Furthermore, if two operators satisfy the connection, then must be a dilation, and an erosion.
Pairs of erosions and dilations satisfying the above connection are called "adjunctions", and the erosion is said to be the adjoint erosion of the dilation, and vice versa.
Opening and closing
For every adjunction , the morphological opening and morphological closing are defined as follows: : : The morphological opening and closing are particular cases of algebraic opening (or simply opening) and algebraic closing (or simply closing). Algebraic openings are operators in ''L'' that are idempotent, increasing, and anti-extensive. Algebraic closings are operators in ''L'' that are idempotent, increasing, and extensive.Particular cases
Binary morphology is a particular case of lattice morphology, where ''L'' is thepower set
In mathematics, the power set (or powerset) of a set is the set of all subsets of , including the empty set and itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is post ...
of ''E'' (Euclidean space or grid), that is, ''L'' is the set of all subsets of ''E'', and is the set inclusion
In mathematics, set ''A'' is a subset of a set ''B'' if all elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ...
. In this case, the infimum is set intersection, and the supremum is set union
In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other.
A refers to a union of ze ...
.
Similarly, grayscale morphology is another particular case, where ''L'' is the set of functions mapping ''E'' into , and , , and , are the point-wise order, supremum, and infimum, respectively. That is, is ''f'' and ''g'' are functions in ''L'', then if and only if ; the infimum is given by ; and the supremum is given by .
See also
* H-maxima transformNotes
References
* ''Image Analysis and Mathematical Morphology'' by Jean Serra, (1982) * ''Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances'' by Jean Serra, (1988) * ''An Introduction to Morphological Image Processing'' by Edward R. Dougherty, (1992) * ''Morphological Image Analysis; Principles and Applications'' by Pierre Soille, (1999), 2nd edition (2003) * ''Mathematical Morphology and its Application to Signal Processing'', J. Serra and Ph. Salembier (Eds.), proceedings of the 1st International workshop on mathematical morphology and its applications to signal processing (ISMM'93), (1993) * ''Mathematical Morphology and Its Applications to Image Processing'', J. Serra and P. Soille (Eds.), proceedings of the 2nd international symposium on mathematical morphology (ISMM'94), (1994) * ''Mathematical Morphology and its Applications to Image and Signal Processing'', Henk J.A.M. Heijmans and Jos B.T.M. Roerdink (Eds.), proceedings of the 4th international symposium on mathematical morphology (ISMM'98), (1998) * ''Mathematical Morphology: 40 Years On'', Christian Ronse, Laurent Najman, and Etienne Decencière (Eds.), (2005) * ''Mathematical Morphology and its Applications to Signal and Image Processing'', Gerald J.F. Banon, Junior Barrera, Ulisses M. Braga-Neto (Eds.), proceedings of the 8th international symposium on mathematical morphology (ISMM'07), (2007) * ''Mathematical morphology: from theory to applications'', Laurent Najman and Hugues Talbot (Eds). ISTE-Wiley. {{ISBN, 978-1-84821-215-2. (520 pp.) June 2010External links
Online course on mathematical morphology
by Jean Serra (in English, French, and Spanish)
Center of Mathematical Morphology
Paris School of Mines
History of Mathematical Morphology
by Georges Matheron and Jean Serra
Morphology Digest, a newsletter on mathematical morphology
by Pierre Soille
Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lectures 16-18 are on Mathematical Morphology
by Alan Peters
by Robyn Owens
SMIL - A Simple (but efficient) Morphological Image Library (from Ecole des Mines de Paris)
Free SIMD Optimized Image processing library
FILTERS : a free open source image processing library
* ttp://www.johanneshjorth.se/SynD Morphological analysis of neurons using Matlab Digital geometry Image processing