Module (gears) on:
[Wikipedia]
[Google]
[Amazon]
 A gear or gearwheel is a rotating machine part typically used to transmit
A gear or gearwheel is a rotating machine part typically used to transmit
in the ''Oxford Learner's Dictionary'' online. Accessed on 2024-07-29.Definition of "cog"
in the ''Merriam-Webster Dictionary'' online. Accessed on 2024-07-29.Definition of "cog"
in the ''Cambridge Dictionary Plus'' online. Accessed on 2024-07-29. or the whole gear.Definition of "cog"
in the ''Collins English Dictionary'' online. Accessed on 2024-07-29. Two or more meshing gears are called a Gears are among the most common mechanical parts. They come in a great variety of shapes and materials, and are used for many different functions and applications. Diameters may range from a few μm in micromachines,Shuailong Zhang, Mohamed Elsayed, Ran Peng,
Yujie Chen (2021): "Reconfigurable multi-component micromachines driven by optoelectronic tweezers". ''Nature Communications'', volume 12, issue 1. to a few mm in
Gears are among the most common mechanical parts. They come in a great variety of shapes and materials, and are used for many different functions and applications. Diameters may range from a few μm in micromachines,Shuailong Zhang, Mohamed Elsayed, Ran Peng,
Yujie Chen (2021): "Reconfigurable multi-component micromachines driven by optoelectronic tweezers". ''Nature Communications'', volume 12, issue 1. to a few mm in
"MY GEAR is Bigger than YOUR GEAR: Industry Battles it Out for World's Largest Gear Title"
Online article from ''Gear Technology'' magazine
Archived on 2024-07-30
Other types of parts that are somewhat similar in shape and function to gears include the
On the Origin of Clockwork, Perpetual Motion Devices, and the Compass
p.84 (Zhan Guo times – Late East
''Economic History of Medieval India, 1200-1500'', page 53
 The gears of the Antikythera mechanism are made of
The gears of the Antikythera mechanism are made of  Still, because of cost or other considerations, some early metal gears had wooden cogs, each tooth forming a type of specialised 'through' mortise and tenon joint
More recently
Still, because of cost or other considerations, some early metal gears had wooden cogs, each tooth forming a type of specialised 'through' mortise and tenon joint
More recently  In spite of the advantages of metal and plastic, wood continued to be used for large gears until a couple of centuries ago, because of cost, weight, tradition, or other considerations. In 1967 the Thompson Manufacturing Company of
In spite of the advantages of metal and plastic, wood continued to be used for large gears until a couple of centuries ago, because of cost, weight, tradition, or other considerations. In 1967 the Thompson Manufacturing Company of
 The gears in a matching pair are said to be ''skew'' if their axes of rotation are skew lines -- neither parallel nor intersecting.
In this case, the best shape for each pitch surface is neither cylindrical nor conical but a portion of a
The gears in a matching pair are said to be ''skew'' if their axes of rotation are skew lines -- neither parallel nor intersecting.
In this case, the best shape for each pitch surface is neither cylindrical nor conical but a portion of a
 A gear is said to be ''external'' if its teeth are directed generally away from the rotation axis, and ''internal'' otherwise. In a pair of matching wheels, only one of them (the larger one) may be internal.
A gear is said to be ''external'' if its teeth are directed generally away from the rotation axis, and ''internal'' otherwise. In a pair of matching wheels, only one of them (the larger one) may be internal.
 In a ''helical'' or ''dry fixed'' gear the tooth walls are not parallel to the axis of rotation, but are set at an angle. An imaginary pitch surface (cylinder, cone, or hyperboloid, depending on the relative axis positions) intersects each tooth face along an arc of a
In a ''helical'' or ''dry fixed'' gear the tooth walls are not parallel to the axis of rotation, but are set at an angle. An imaginary pitch surface (cylinder, cone, or hyperboloid, depending on the relative axis positions) intersects each tooth face along an arc of a  The angled teeth engage more gradually than do spur gear teeth, causing them to run more smoothly and quietly. With parallel helical gears, each pair of teeth first make contact at a single point at one side of the gear wheel; a moving curve of contact then grows gradually across the tooth face to a maximum, then recedes until the teeth break contact at a single point on the opposite side. In spur gears, teeth suddenly meet at a line contact across their entire width, causing stress and noise. Spur gears make a characteristic whine at high speeds. For this reason spur gears are used in low-speed applications and in situations where noise control is not a problem, and helical gears are used in high-speed applications, large power transmission, or where noise abatement is important. The speed is considered high when the pitch line velocity exceeds 25 m/s.
A disadvantage of helical gears is a resultant
The angled teeth engage more gradually than do spur gear teeth, causing them to run more smoothly and quietly. With parallel helical gears, each pair of teeth first make contact at a single point at one side of the gear wheel; a moving curve of contact then grows gradually across the tooth face to a maximum, then recedes until the teeth break contact at a single point on the opposite side. In spur gears, teeth suddenly meet at a line contact across their entire width, causing stress and noise. Spur gears make a characteristic whine at high speeds. For this reason spur gears are used in low-speed applications and in situations where noise control is not a problem, and helical gears are used in high-speed applications, large power transmission, or where noise abatement is important. The speed is considered high when the pitch line velocity exceeds 25 m/s.
A disadvantage of helical gears is a resultant
3D animation of helical gears (parallel axis)
3D animation of helical gears (crossed axis)

 ''Worms'' resemble
''Worms'' resemble
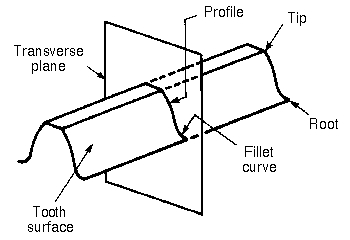 Another criterion to classify gears is the ''tooth profile'', the shape of the cross-section of a tooth face by an imaginary cut perpendicular to the pitch surface, such as the transverse, normal, or axial plane.
The tooth profile is crucial for the smoothness and uniformity of the movement of matching gears, as well as for the
Another criterion to classify gears is the ''tooth profile'', the shape of the cross-section of a tooth face by an imaginary cut perpendicular to the pitch surface, such as the transverse, normal, or axial plane.
The tooth profile is crucial for the smoothness and uniformity of the movement of matching gears, as well as for the
 The teeth of antique or artisanal gears that were cut by hand from sheet material, like those in the Antikhytera mechanism, generally had simple profiles, such as triangles.
The teeth of larger gears — such as used in windmills — were usually pegs with simple shapes like cylinders,
The teeth of antique or artisanal gears that were cut by hand from sheet material, like those in the Antikhytera mechanism, generally had simple profiles, such as triangles.
The teeth of larger gears — such as used in windmills — were usually pegs with simple shapes like cylinders,
 A ''cage gear'', also called a ''lantern gear'' or ''lantern pinion'', is one of those artisanal gears having cylindrical rods for teeth, parallel to the axle and arranged in a circle around it, much as the bars on a round bird cage or lantern. The assembly is held together by disks at each end, into which the tooth rods and axle are set. Cage gears are more efficient than solid pinions, and dirt can fall through the rods rather than becoming trapped and increasing wear. They can be constructed with very simple tools as the teeth are not formed by cutting or milling, but rather by drilling holes and inserting rods.
Sometimes used in clocks, a cage gear should always be driven by a gearwheel, not used as the driver. The cage gear was not initially favoured by conservative clock makers. It became popular in turret clocks where dirty working conditions were most commonplace. Domestic American clock movements often used them.
A ''cage gear'', also called a ''lantern gear'' or ''lantern pinion'', is one of those artisanal gears having cylindrical rods for teeth, parallel to the axle and arranged in a circle around it, much as the bars on a round bird cage or lantern. The assembly is held together by disks at each end, into which the tooth rods and axle are set. Cage gears are more efficient than solid pinions, and dirt can fall through the rods rather than becoming trapped and increasing wear. They can be constructed with very simple tools as the teeth are not formed by cutting or milling, but rather by drilling holes and inserting rods.
Sometimes used in clocks, a cage gear should always be driven by a gearwheel, not used as the driver. The cage gear was not initially favoured by conservative clock makers. It became popular in turret clocks where dirty working conditions were most commonplace. Domestic American clock movements often used them.
 For non-parallel axes with non-straight tooth cuts, the best tooth profile is one of several spiral bevel gear shapes. These include Gleason types (circular arc with non-constant tooth depth), Oerlikon and Curvex types (circular arc with constant tooth depth), Klingelnberg Cyclo-Palloid (Epicycloid with constant tooth depth) or Klingelnberg Palloid..
The tooth faces in these gear types are not involute cylinders or cones but patches of octoidal surfaces. Manufacturing such tooth faces may require a 5-axis
For non-parallel axes with non-straight tooth cuts, the best tooth profile is one of several spiral bevel gear shapes. These include Gleason types (circular arc with non-constant tooth depth), Oerlikon and Curvex types (circular arc with constant tooth depth), Klingelnberg Cyclo-Palloid (Epicycloid with constant tooth depth) or Klingelnberg Palloid..
The tooth faces in these gear types are not involute cylinders or cones but patches of octoidal surfaces. Manufacturing such tooth faces may require a 5-axis
 A ''rack'' is a toothed bar or rod that can be thought of as a sector gear with an infinitely large
A ''rack'' is a toothed bar or rod that can be thought of as a sector gear with an infinitely large
 In epicyclic gearing, one or more of the gear
In epicyclic gearing, one or more of the gear
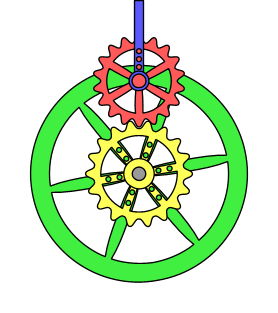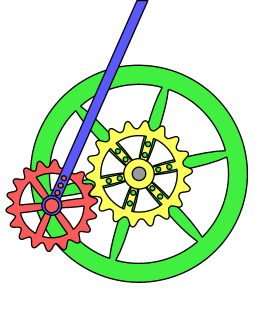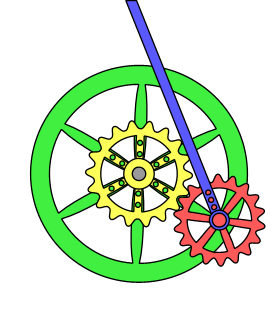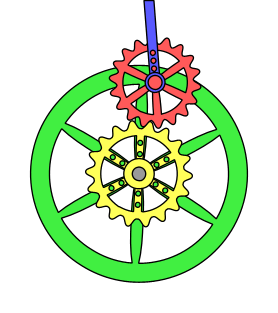
 Non-circular gears are designed for special purposes. While a regular gear is optimized to transmit torque to another engaged member with minimum noise and wear and maximum
Non-circular gears are designed for special purposes. While a regular gear is optimized to transmit torque to another engaged member with minimum noise and wear and maximum
 A ''harmonic gear'' or '' strain wave gear'' is a specialized gearing mechanism often used in industrial
A ''harmonic gear'' or '' strain wave gear'' is a specialized gearing mechanism often used in industrial
 ; Rotational
; Rotational
File:Contact line.jpg, Line of contact
File:Action path.jpg, Path of action
File:Action line.jpg, Line of action
File:Action plane.jpg, Plane of action
File:Contact lines.jpg, Lines of contact (helical gear)
File:Action arc.jpg, Arc of action
File:Action length.jpg, Length of action
File:Limit diameter.jpg, Limit diameter
File:Face advance.svg, Face advance
File:Action zone.jpg, Zone of action
; Point of contact : Any point at which two tooth profiles touch each other.
; Line of contact : A line or curve along which two tooth surfaces are tangent to each other.
; Path of action : The locus of successive contact points between a pair of gear teeth, during the phase of engagement. For conjugate gear teeth, the path of action passes through the pitch point. It is the trace of the surface of action in the plane of rotation.
; Line of action : The path of action for involute gears. It is the straight line passing through the pitch point and tangent to both base circles.
; Surface of action : The imaginary surface in which contact occurs between two engaging tooth surfaces. It is the summation of the paths of action in all sections of the engaging teeth.
; Plane of action: The surface of action for involute, parallel axis gears with either spur or helical teeth. It is tangent to the base cylinders.
; Zone of action (contact zone) : For involute, parallel-axis gears with either spur or helical teeth, is the rectangular area in the plane of action bounded by the length of action and the effective face width.
; Path of contact: The curve on either tooth surface along which theoretical single point contact occurs during the engagement of gears with crowned tooth surfaces or gears that normally engage with only single point contact.
; Length of action: The distance on the line of action through which the point of contact moves during the action of the tooth profile.
; Arc of action, ''Qt'' : The arc of the pitch circle through which a tooth profile moves from the beginning to the end of contact with a mating profile.
; Arc of approach, ''Qa'' : The arc of the pitch circle through which a tooth profile moves from its beginning of contact until the point of contact arrives at the pitch point.
; Arc of recess, ''Qr'' : The arc of the pitch circle through which a tooth profile moves from contact at the pitch point until contact ends.
; Contact ratio, ''mc'' or ''ε'' : The number of angular pitches through which a tooth surface rotates from the beginning to the end of contact. In a simple way, it can be defined as a measure of the average number of teeth in contact during the period during which a tooth comes and goes out of contact with the mating gear.
; Transverse contact ratio, ''mp'' or ''εα'' : The contact ratio in a transverse plane. It is the ratio of the angle of action to the angular pitch. For involute gears it is most directly obtained as the ratio of the length of action to the base pitch.
; Face contact ratio, ''mF'' or ''εβ'' : The contact ratio in an axial plane, or the ratio of the face width to the axial pitch. For bevel and hypoid gears it is the ratio of face advance to circular pitch.
; Total contact ratio, ''mt'' or ''εγ'' : The sum of the transverse contact ratio and the face contact ratio.
::
::
; Modified contact ratio, ''mo'' : For bevel gears, the square root of the sum of the squares of the transverse and face contact ratios.
::
; Limit diameter : Diameter on a gear at which the line of action intersects the maximum (or minimum for internal pinion) addendum circle of the mating gear. This is also referred to as the start of active profile, the start of contact, the end of contact, or the end of active profile.
; Start of active profile (SAP) : Intersection of the limit diameter and the involute profile.
; Face advance : Distance on a pitch circle through which a helical or spiral tooth moves from the position at which contact begins at one end of the tooth trace on the pitch surface to the position where contact ceases at the other end.
File:Tooth thickness.jpg, Tooth thickness
File:Thickness relationships.jpg, Thickness relationships
File:Chordial thickness.svg, Chordal thickness
File:Pin measurement.jpg, Tooth thickness measurement over pins
File:Span measurement.jpg, Span measurement
File:Addendum teeth.jpg, Long and short addendum teeth
; Circular thickness : Length of arc between the two sides of a gear tooth, on the specified datum circle.
; Transverse circular thickness : Circular thickness in the transverse plane.
; Normal circular thickness : Circular thickness in the normal plane. In a helical gear it may be considered as the length of arc along a normal helix.
; Axial thickness: In helical gears and worms, tooth thickness in an axial cross section at the standard pitch diameter.
; Base circular thickness: In involute teeth, length of arc on the base circle between the two involute curves forming the profile of a tooth.
; Normal chordal thickness: Length of the chord that subtends a circular thickness arc in the plane normal to the pitch helix. Any convenient measuring diameter may be selected, not necessarily the standard pitch diameter.
; Chordal addendum (chordal height) : Height from the top of the tooth to the chord subtending the circular thickness arc. Any convenient measuring diameter may be selected, not necessarily the standard pitch diameter.
; Profile shift : Displacement of the basic rack datum line from the reference cylinder, made non-dimensional by dividing by the normal module. It is used to specify the tooth thickness, often for zero backlash.
; Rack shift : Displacement of the tool datum line from the reference cylinder, made non-dimensional by dividing by the normal module. It is used to specify the tooth thickness.
; Measurement over pins : Measurement of the distance taken over a pin positioned in a tooth space and a reference surface. The reference surface may be the reference axis of the gear, a datum surface or either one or two pins positioned in the tooth space or spaces opposite the first. This measurement is used to determine tooth thickness.
; Span measurement : Measurement of the distance across several teeth in a normal plane. As long as the measuring device has parallel measuring surfaces that contact on an unmodified portion of the involute, the measurement wis along a line tangent to the base cylinder. It is used to determine tooth thickness.
; Modified addendum teeth : Teeth of engaging gears, one or both of which have non-standard addendum.
; Full-depth teeth : Teeth in which the working depth equals 2.000 divided by the normal diametral pitch.
; Stub teeth : Teeth in which the working depth is less than 2.000 divided by the normal diametral pitch.
; Equal addendum teeth : Teeth in which two engaging gears have equal addendums.
; Long and short-addendum teeth : Teeth in which the addendums of two engaging gears are unequal.
 ; Undercut : An undercut is a condition in generated gear teeth when any part of the fillet curve lies inside of a line drawn tangent to the working profile at its point of juncture with the fillet. Undercut may be deliberately introduced to facilitate finishing operations. With undercut the fillet curve intersects the working profile. Without undercut the fillet curve and the working profile have a common tangent.
; Root fillet : or fillet curve, the concave portion of the tooth profile where it joins the bottom of the tooth space. 2
; Undercut : An undercut is a condition in generated gear teeth when any part of the fillet curve lies inside of a line drawn tangent to the working profile at its point of juncture with the fillet. Undercut may be deliberately introduced to facilitate finishing operations. With undercut the fillet curve intersects the working profile. Without undercut the fillet curve and the working profile have a common tangent.
; Root fillet : or fillet curve, the concave portion of the tooth profile where it joins the bottom of the tooth space. 2
File:Pitches.svg, Pitch
File:Tooth pitches.jpg, Tooth pitch
File:Base pitch.jpg, Base pitch relationships
File:Principal pitches.jpg, Principal pitches
; Circular pitch, ''p'' : Arc distance along a specified pitch circle or pitch line between corresponding profiles of adjacent teeth.
; Transverse circular pitch, ''p''t : Circular pitch in the transverse plane.
; Normal circular pitch, ''p''n, ''p''e : Circular pitch in the normal plane, and also the length of the arc along the normal pitch helix between helical teeth or threads.
; Axial pitch, ''p''x : Linear pitch in an axial plane and in a pitch surface. In helical gears and worms, axial pitch has the same value at all diameters. In gearing of other types, axial pitch may be confined to the pitch surface and may be a circular measurement. The term axial pitch is preferred to the term linear pitch. The axial pitch of a helical worm and the circular pitch of its worm gear are the same.
; Normal base pitch, ''p''N, ''p''bn :An involute helical gear is the base pitch in the normal plane. It is the normal distance between parallel helical involute surfaces on the plane of action in the normal plane, or is the length of arc on the normal base helix. It is a constant distance in any helical involute gear.
; Transverse base pitch, ''p''b, ''p''bt : In an involute gear, the pitch is on the base circle or along the line of action. Corresponding sides of involute gear teeth are parallel curves, and the base pitch is the constant and fundamental distance between them along a common normal in a transverse plane.
; Diametral pitch (transverse), ''P''d : Ratio of the number of teeth to the standard pitch diameter in inches.
::
; Normal diametral pitch, ''P''nd : Value of diametral pitch in a normal plane of a helical gear or worm.
::
; Angular pitch, ''θ''N, ''τ'' : Angle subtended by the circular pitch, usually expressed in radians.
:: degrees or radians
 The gear mechanism was previously considered exclusively artificial, but as early as 1957, gears had been recognized in the hind legs of various species of
The gear mechanism was previously considered exclusively artificial, but as early as 1957, gears had been recognized in the hind legs of various species of
"Wheels That Can't Slip."
''Popular Science'', February 1945, pp. 120–125.
Geararium. Museum of gears and toothed wheels
- antique and vintage gears, sprockets, ratchets and other gear-related objects.
Kinematic Models for Design Digital Library (KMODDL)
- movies and photos of hundreds of working models at Cornell University
Short historical account on the application of analytical geometry to the form of gear teethMathematical Tutorial for Gearing (Relating to Robotics)American Gear Manufacturers AssociationGear Technology, the Journal of Gear Manufacturing
{{Kinematic pair Tribology Articles containing video clips
 A gear or gearwheel is a rotating machine part typically used to transmit
A gear or gearwheel is a rotating machine part typically used to transmit rotational motion
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis interse ...
and/or torque
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. Wh ...
by means of a series of teeth that engage with compatible teeth of another gear or other part. The teeth can be integral saliences or cavities machined on the part, or separate pegs inserted into it. In the latter case, the gear is usually called a cogwheel. A cog may be one of those pegsDefinition of "cog"in the ''Oxford Learner's Dictionary'' online. Accessed on 2024-07-29.Definition of "cog"
in the ''Merriam-Webster Dictionary'' online. Accessed on 2024-07-29.Definition of "cog"
in the ''Cambridge Dictionary Plus'' online. Accessed on 2024-07-29. or the whole gear.Definition of "cog"
in the ''Collins English Dictionary'' online. Accessed on 2024-07-29. Two or more meshing gears are called a
gear train
A gear train or gear set is a machine element of a mechanical system formed by mounting two or more gears on a frame such that the teeth of the gears engage.
Gear teeth are designed to ensure the pitch circles of engaging gears roll on each oth ...
.
The smaller member of a pair of meshing gears is often called pinion. Most commonly, gears and gear trains can be used to trade torque
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. Wh ...
for rotational speed
Rotational frequency, also known as rotational speed or rate of rotation (symbols ''ν'', lowercase Greek nu, and also ''n''), is the frequency of rotation of an object around an axis.
Its SI unit is the reciprocal seconds (s−1); other com ...
between two axle
An axle or axletree is a central shaft for a rotation, rotating wheel and axle, wheel or gear. On wheeled vehicles, the axle may be fixed to the wheels, rotating with them, or fixed to the vehicle, with the wheels rotating around the axle. In ...
s or other rotating parts and/or to change the axis of rotation and/or to invert the sense of rotation. A gear may also be used to transmit linear force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
and/or linear motion
Linear motion, also called rectilinear motion, is one-dimensional motion along a straight line, and can therefore be described mathematically using only one spatial dimension. The linear motion can be of two types: uniform linear motion, with ...
to a rack, a straight bar with a row of compatible teeth.
 Gears are among the most common mechanical parts. They come in a great variety of shapes and materials, and are used for many different functions and applications. Diameters may range from a few μm in micromachines,Shuailong Zhang, Mohamed Elsayed, Ran Peng,
Yujie Chen (2021): "Reconfigurable multi-component micromachines driven by optoelectronic tweezers". ''Nature Communications'', volume 12, issue 1. to a few mm in
Gears are among the most common mechanical parts. They come in a great variety of shapes and materials, and are used for many different functions and applications. Diameters may range from a few μm in micromachines,Shuailong Zhang, Mohamed Elsayed, Ran Peng,
Yujie Chen (2021): "Reconfigurable multi-component micromachines driven by optoelectronic tweezers". ''Nature Communications'', volume 12, issue 1. to a few mm in watch
A watch is a timepiece carried or worn by a person. It is designed to maintain a consistent movement despite the motions caused by the person's activities. A wristwatch is worn around the wrist, attached by a watch strap or another type of ...
es and toys to over 10 metre
The metre (or meter in US spelling; symbol: m) is the base unit of length in the International System of Units (SI). Since 2019, the metre has been defined as the length of the path travelled by light in vacuum during a time interval of of ...
s in some mining equipment.Matthew Jaster (2013)"MY GEAR is Bigger than YOUR GEAR: Industry Battles it Out for World's Largest Gear Title"
Online article from ''Gear Technology'' magazine
Archived on 2024-07-30
Other types of parts that are somewhat similar in shape and function to gears include the
sprocket
A sprocket, sprocket-wheel or chainwheel is a profiled wheel
A wheel is a rotating component (typically circular in shape) that is intended to turn on an axle Bearing (mechanical), bearing. The wheel is one of the key components of the whe ...
, which is meant to engage with a link chain
A chain is a wikt:series#Noun, serial assembly of connected pieces, called links, typically made of metal, with an overall character similar to that of a rope in that it is flexible and curved in compression (physics), compression but line (g ...
instead of another gear, and the timing pulley, meant to engage a timing belt. Most gears are round and have equal teeth, designed to operate as smoothly as possible; but there are several applications for non-circular gear
A non-circular gear (NCG) is a special gear design with special characteristics and purpose. While a regular gear is optimized to transmit torque to another engaged member with minimum noise and wear and with maximum Mechanical efficiency, effic ...
s, and the Geneva drive
The Geneva drive or Geneva mechanism is a gear mechanism that translates a continuous rotation movement into intermittent rotary motion.
The ''rotating drive'' wheel is usually equipped with a pin that reaches into a slot located in the other ...
has an extremely uneven operation, by design.
Gears can be seen as instances of the basic lever
A lever is a simple machine consisting of a beam (structure), beam or rigid rod pivoted at a fixed hinge, or '':wikt:fulcrum, fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, l ...
"machine". When a small gear drives a larger one, the mechanical advantage
Mechanical advantage is a measure of the force amplification achieved by using a tool, mechanical device or machine system. The device trades off input forces against movement to obtain a desired amplification in the output force. The model for ...
of this ideal lever causes the torque ''T'' to increase but the rotational speed
Rotational frequency, also known as rotational speed or rate of rotation (symbols ''ν'', lowercase Greek nu, and also ''n''), is the frequency of rotation of an object around an axis.
Its SI unit is the reciprocal seconds (s−1); other com ...
''ω'' to decrease. The opposite effect is obtained when a large gear drives a small one. The changes are proportional to the ''gear ratio'' ''r'', the ratio of the tooth counts: namely, , and . Depending on the geometry of the pair, the sense of rotation may also be inverted (from clockwise to anti-clockwise, or vice versa).
Most vehicles have a transmission or "gearbox" containing a set of gears that can be meshed in multiple configurations. The gearbox lets the operator vary the torque that is applied to the wheels without changing the engine's speed. Gearboxes are used also in many other machines, such as lathe
A lathe () is a machine tool that rotates a workpiece about an axis of rotation to perform various operations such as cutting, sanding, knurling, drilling, deformation, facing, threading and turning, with tools that are applied to the w ...
s and conveyor belts. In all those cases, terms like "first gear", "high gear", and "reverse gear" refer to the overall torque ratios of different meshing configurations, rather than to specific physical gears. These terms may be applied even when the vehicle does not actually contain gears, as in a continuously variable transmission
A continuously variable transmission (CVT) is an automated Transmission (mechanical device), transmission that can change through a continuous range of gear ratios, typically resulting in better fuel economy in gasoline applications. This contr ...
.
History
The oldest functioning gears by far are not man made, but are seen in the hind legs of the nymphs of the planthopper insect '' Issus coleoptratus''. The earliest man-made gears that have not been lost or destroyed date to 4th century BCChina
China, officially the People's Republic of China (PRC), is a country in East Asia. With population of China, a population exceeding 1.4 billion, it is the list of countries by population (United Nations), second-most populous country after ...
Derek J. de Solla Price
Derek John de Solla Price (22 January 1922 – 3 September 1983) was a British physicist, history of science, historian of science, and information science, information scientist. He was known for his investigation of the Antikythera mechanism, ...
On the Origin of Clockwork, Perpetual Motion Devices, and the Compass
p.84 (Zhan Guo times – Late East
Zhou dynasty
The Zhou dynasty ( ) was a royal dynasty of China that existed for 789 years from until 256 BC, the longest span of any dynasty in Chinese history. During the Western Zhou period (771 BC), the royal house, surnamed Ji, had military ...
), which have been preserved at the Luoyang Museum of Henan Province, China
China, officially the People's Republic of China (PRC), is a country in East Asia. With population of China, a population exceeding 1.4 billion, it is the list of countries by population (United Nations), second-most populous country after ...
.
In Europe, Aristotle
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
mentions gears around 330 BC, as wheel drives in windlasses. He observed that the direction of rotation is reversed when one gear wheel drives another gear wheel. Philon of Byzantium was one of the first who used gears in water raising devices. Gears appear in works connected to Hero of Alexandria
Hero of Alexandria (; , , also known as Heron of Alexandria ; probably 1st or 2nd century AD) was a Greek mathematician and engineer who was active in Alexandria in Egypt during the Roman era. He has been described as the greatest experimental ...
, in Roman Egypt
Roman Egypt was an imperial province of the Roman Empire from 30 BC to AD 642. The province encompassed most of modern-day Egypt except for the Sinai. It was bordered by the provinces of Crete and Cyrenaica to the west and Judaea, ...
circa AD 50, but can be traced back to the mechanics of the Library of Alexandria
The Great Library of Alexandria in Alexandria, Egypt, was one of the largest and most significant libraries of the ancient world. The library was part of a larger research institution called the Mouseion, which was dedicated to the Muses, ...
in 3rd-century BC Ptolemaic Egypt Ptolemaic is the adjective formed from the name Ptolemy, and may refer to:
Pertaining to the Ptolemaic dynasty
* Ptolemaic dynasty, the Macedonian Greek dynasty that ruled Egypt founded in 305 BC by Ptolemy I Soter
*Ptolemaic Kingdom
Pertaining ...
, and were greatly developed by the Greek polymath
A polymath or polyhistor is an individual whose knowledge spans many different subjects, known to draw on complex bodies of knowledge to solve specific problems. Polymaths often prefer a specific context in which to explain their knowledge, ...
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
(287–212 BC). The earliest surviving gears in Europe were found in the Antikythera mechanism
The Antikythera mechanism ( , ) is an Ancient Greece, Ancient Greek hand-powered orrery (model of the Solar System). It is the oldest known example of an Analog computer, analogue computer. It could be used to predict astronomy, astronomical ...
an example of a very early and intricate geared device, designed to calculate astronomical
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest include ...
positions of the sun, moon, and planets, and predict eclipse
An eclipse is an astronomical event which occurs when an astronomical object or spacecraft is temporarily obscured, by passing into the shadow of another body or by having another body pass between it and the viewer. This alignment of three ...
s. Its time of construction is now estimated between 150 and 100 BC.
The Chinese engineer Ma Jun (–265) described a south-pointing chariot
The south-pointing chariot (or carriage) was an ancient Chinese two-wheeled vehicle that carried a movable pointer to indicate the south, no matter how the chariot turned. Usually, the pointer took the form of a doll or figure with an outstretch ...
. A set of differential gears connected to the wheels and to a pointer on top of the chariot kept the direction of latter unchanged as the chariot turned.
Another early surviving example of geared mechanism is a complex calendrical device showing the phase of the Moon, the day of the month and the places of the Sun and the Moon in the Zodiac was invented in the Byzantine empire in the early 6th century.
Geared mechanical water clocks were built in China
China, officially the People's Republic of China (PRC), is a country in East Asia. With population of China, a population exceeding 1.4 billion, it is the list of countries by population (United Nations), second-most populous country after ...
by 725.
Around 1221, a geared astrolabe
An astrolabe (; ; ) is an astronomy, astronomical list of astronomical instruments, instrument dating to ancient times. It serves as a star chart and Model#Physical model, physical model of the visible celestial sphere, half-dome of the sky. It ...
was built in Isfahan
Isfahan or Esfahan ( ) is a city in the Central District (Isfahan County), Central District of Isfahan County, Isfahan province, Iran. It is the capital of the province, the county, and the district. It is located south of Tehran. The city ...
showing the position of the moon
The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). The Moon rotation, rotates, with a rotation period (lunar ...
in the zodiac
The zodiac is a belt-shaped region of the sky that extends approximately 8° north and south celestial latitude of the ecliptic – the apparent path of the Sun across the celestial sphere over the course of the year. Within this zodiac ...
and its phase, and the number of days since new moon.
The worm gear
A worm drive is a gear train, gear arrangement in which a worm (which is a gear in the form of a Screw thread, screw) meshes with a worm wheel (which is similar in appearance to a spur gear). Its main purpose is to translate the motion of two p ...
was invented in the Indian subcontinent
The Indian subcontinent is a physiographic region of Asia below the Himalayas which projects into the Indian Ocean between the Bay of Bengal to the east and the Arabian Sea to the west. It is now divided between Bangladesh, India, and Pakista ...
, for use in roller cotton gin
A cotton gin—meaning "cotton engine"—is a machine that quickly and easily separates cotton fibers from their seeds, enabling much greater productivity than manual cotton separation.. Reprinted by McGraw-Hill, New York and London, 1926 (); ...
s, some time during the 13th–14th centuries.Irfan Habib
Irfan Habib (born 10 August 1931) is an Indian historian of ancient and medieval India, following the methodology of Marxist historiography in his contributions to economic history. He is known for his strong stance against Hindutva. He has au ...
''Economic History of Medieval India, 1200-1500'', page 53
Pearson Education
Pearson Education, known since 2011 as simply Pearson, is the educational publishing and services subsidiary of the international corporation Pearson plc. The subsidiary was formed in 1998, when Pearson plc acquired Simon & Schuster's educatio ...
A complex astronomical clock, called the Astrarium, was built between 1348 and 1364 by Giovanni Dondi dell'Orologio. It had seven faces and 107 moving parts; it showed the positions of the sun, the moon and the five planets then known, as well as religious feast days. The Salisbury Cathedral clock, built in 1386, it is the world's oldest still working geared mechanical clock.
Differential gears were used by the British clock maker Joseph Williamson in 1720.
Etymology
The word ''gear'' is probably fromOld Norse
Old Norse, also referred to as Old Nordic or Old Scandinavian, was a stage of development of North Germanic languages, North Germanic dialects before their final divergence into separate Nordic languages. Old Norse was spoken by inhabitants ...
''gørvi'' (plural ''gørvar'') 'apparel, gear,' related to ''gøra'', ''gørva'' 'to make, construct, build; set in order, prepare,' a common verb in Old Norse, "used in a wide range of situations from writing a book to dressing meat". In this context, the meaning of 'toothed wheel in machinery' first attested 1520s; specific mechanical sense of 'parts by which a motor communicates motion' is from 1814; specifically of a vehicle (bicycle, automobile, etc.) by 1888.
A ''cog'' is a tooth on a wheel. From Middle English
Middle English (abbreviated to ME) is a form of the English language that was spoken after the Norman Conquest of 1066, until the late 15th century. The English language underwent distinct variations and developments following the Old English pe ...
cogge, from Old Norse
Old Norse, also referred to as Old Nordic or Old Scandinavian, was a stage of development of North Germanic languages, North Germanic dialects before their final divergence into separate Nordic languages. Old Norse was spoken by inhabitants ...
(compare Norwegian ''kugg'' ('cog'), Swedish ''kugg'', ''kugge'' ('cog, tooth')), from Proto-Germanic
Proto-Germanic (abbreviated PGmc; also called Common Germanic) is the linguistic reconstruction, reconstructed proto-language of the Germanic languages, Germanic branch of the Indo-European languages.
Proto-Germanic eventually developed from ...
*''kuggō'' (compare Dutch ''kogge'' (' cogboat'), German ''Kock''), from Proto-Indo-European
Proto-Indo-European (PIE) is the reconstructed common ancestor of the Indo-European language family. No direct record of Proto-Indo-European exists; its proposed features have been derived by linguistic reconstruction from documented Indo-Euro ...
*''gugā'' ('hump, ball') (compare Lithuanian ''gugà'' ('pommel, hump, hill'), from PIE *''gēw-'' ('to bend, arch'). First used c. 1300 in the sense of 'a wheel having teeth or cogs; late 14c., 'tooth on a wheel'; cog-wheel, early 15c.
Materials
 The gears of the Antikythera mechanism are made of
The gears of the Antikythera mechanism are made of bronze
Bronze is an alloy consisting primarily of copper, commonly with about 12–12.5% tin and often with the addition of other metals (including aluminium, manganese, nickel, or zinc) and sometimes non-metals (such as phosphorus) or metalloid ...
, and the earliest surviving Chinese gears are made of iron. These metals, as well as tin, have been generally used for clocks and similar mechanisms to this day.
Historically, large gears, such as those used in flour mills, were commonly made of wood rather than metal. They were cogwheels, made by inserting a series of wooden pegs or cogs around the rim of a wheel. The cogs were often made of maple
''Acer'' is a genus of trees and shrubs commonly known as maples. The genus is placed in the soapberry family Sapindaceae.Stevens, P. F. (2001 onwards). Angiosperm Phylogeny Website. Version 9, June 2008 nd more or less continuously updated si ...
wood.
Wooden gears have been gradually replaced by ones made or metal, such as cast iron
Cast iron is a class of iron–carbon alloys with a carbon content of more than 2% and silicon content around 1–3%. Its usefulness derives from its relatively low melting temperature. The alloying elements determine the form in which its car ...
at first, then steel
Steel is an alloy of iron and carbon that demonstrates improved mechanical properties compared to the pure form of iron. Due to steel's high Young's modulus, elastic modulus, Yield (engineering), yield strength, Fracture, fracture strength a ...
and aluminum
Aluminium (or aluminum in North American English) is a chemical element; it has chemical symbol, symbol Al and atomic number 13. It has a density lower than that of other common metals, about one-third that of steel. Aluminium has ...
. Steel is most commonly used because of its high strength-to-weight ratio and low cost. Aluminum is not as strong as steel for the same geometry, but is lighter and easier to machine. Powder metallurgy
Powder metallurgy (PM) is a term covering a wide range of ways in which materials or components are made from metal powders. PM processes are sometimes used to reduce or eliminate the need for subtractive manufacturing, subtractive processes in ma ...
may be used with alloys that cannot be easily cast or machined.
 Still, because of cost or other considerations, some early metal gears had wooden cogs, each tooth forming a type of specialised 'through' mortise and tenon joint
More recently
Still, because of cost or other considerations, some early metal gears had wooden cogs, each tooth forming a type of specialised 'through' mortise and tenon joint
More recently engineering plastic
Engineering plastics are a group of plastic materials that have better mechanical or thermal properties than the more widely used commodity plastics (such as polystyrene, polyvinyl chloride, polypropylene and polyethylene).
Engineering plastic ...
s and composite materials
A composite or composite material (also composition material) is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a ...
have been replacing metals in many applications, especially those with moderate speed and torque. They are not as strong as steel, but are cheaper, can be mass-manufactured by injection molding
Injection moulding (U.S. spelling: injection molding) is a manufacturing process for producing parts by injecting molten material into a mould, or mold. Injection moulding can be performed with a host of materials mainly including metals (for ...
, and don't need lubrication. Plastic gears can even be intentionally designed to be the weakest part in a mechanism, so that in case of jamming they will fail first and thus avoid damage to more expensive parts. Such "sacrificial" gears may be a simpler alternative to other overload-protection devices such as clutches and torque-limited or current-limited motors.
 In spite of the advantages of metal and plastic, wood continued to be used for large gears until a couple of centuries ago, because of cost, weight, tradition, or other considerations. In 1967 the Thompson Manufacturing Company of
In spite of the advantages of metal and plastic, wood continued to be used for large gears until a couple of centuries ago, because of cost, weight, tradition, or other considerations. In 1967 the Thompson Manufacturing Company of Lancaster, New Hampshire
Lancaster is a town located along the Connecticut River in Coös County, New Hampshire, United States. The town is named after the city of Lancaster in England. As of the 2020 census, the town population was 3,218, the second largest in the cou ...
still had a very active business in supplying tens of thousands of maple gear teeth per year, mostly for use in paper mill
A paper mill is a factory devoted to making paper from vegetable fibres such as wood pulp, old rags, and other ingredients. Prior to the invention and adoption of the Fourdrinier machine and other types of paper machine that use an endless belt ...
s and grist mills, some dating back over 100 years.
Manufacture
The most common techniques for gear manufacturing are dies,sand
Sand is a granular material composed of finely divided mineral particles. Sand has various compositions but is usually defined by its grain size. Sand grains are smaller than gravel and coarser than silt. Sand can also refer to a textural ...
, and investment casting; injection molding
Injection moulding (U.S. spelling: injection molding) is a manufacturing process for producing parts by injecting molten material into a mould, or mold. Injection moulding can be performed with a host of materials mainly including metals (for ...
; powder metallurgy
Powder metallurgy (PM) is a term covering a wide range of ways in which materials or components are made from metal powders. PM processes are sometimes used to reduce or eliminate the need for subtractive manufacturing, subtractive processes in ma ...
; blanking; and gear cutting.
As of 2014, an estimated 80% of all gearing produced worldwide is produced by net shape molding. Molded gearing is usually powder metallurgy, plastic injection, or metal die casting. Gears produced by powder metallurgy often require a sintering
Sintering or frittage is the process of compacting and forming a solid mass of material by pressure or heat without melting it to the point of liquefaction. Sintering happens as part of a manufacturing process used with metals, ceramics, plas ...
step after they are removed from the mold. Cast gears require gear cutting or other machining
Machining is a manufacturing process where a desired shape or part is created using the controlled removal of material, most often metal, from a larger piece of raw material by cutting. Machining is a form of subtractive manufacturing, which util ...
to shape the teeth to the necessary precision. The most common form of gear cutting is hobbing, but gear shaping
Gear shaping is a machining process for creating teeth on a gear using a cutter. Gear shaping is a convenient and versatile method of gear cutting. It involves continuous, same-plane rotational cutting of gear.
Process theory
The types of cutt ...
, milling
Milling may refer to:
* Milling (minting), forming narrow ridges around the edge of a coin
* Milling (grinding), breaking solid materials into smaller pieces by grinding, crushing, or cutting in a mill
* Milling (machining), a process of using ro ...
, and broaching may be used instead.
Metal gears intended for heavy duty operation, such as in the transmissions of cars and trucks, the teeth are heat treated to make them hard and more wear resistant while leaving the core soft but tough. For large gears that are prone to warp, a quench press is used.
Gears can be made by 3D printing
3D printing, or additive manufacturing, is the construction of a three-dimensional object from a CAD model or a digital 3D model. It can be done in a variety of processes in which material is deposited, joined or solidified under computer ...
; however, this alternative is typically used only for prototypes or very limited production quantities, because of its high cost, low accuracy, and relatively low strength of the resulting part.
Comparison with other drive mechanisms
Besides gear trains, other alternative methods of transmitting torque between non-coaxial parts includelink chain
A chain is a wikt:series#Noun, serial assembly of connected pieces, called links, typically made of metal, with an overall character similar to that of a rope in that it is flexible and curved in compression (physics), compression but line (g ...
s driven by sprockets, friction drives, belts and pulleys, hydraulic couplings, and timing belts.
One major advantage of gears is that their rigid body and the snug interlocking of the teeth ensure precise tracking of the rotation across the gear train, limited only by backlash and other mechanical defects. For this reason they are favored in precision applications such as watches. Gear trains also can have fewer separate parts (only two) and have minimal power loss, minimal wear, and long life. Gears are also often the most efficient and compact way of transmitting torque between two non-parallel axes.
On the other hand, gears are more expensive to manufacture, may require periodic lubrication, and may have greater mass and rotational inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relatively to a rotational axis. It is the ratio between ...
than the equivalent pulleys. More importantly, the distance between the axes of matched gears is limited and cannot be changed once they are manufactured. There are also applications where slippage under overload or transients (as occurs with belts, hydraulics, and friction wheels) is not only acceptable but desirable.
Ideal gear model
For basic analysis purposes, each gear can be idealized as a perfectlyrigid body
In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible, when a deforming pressure or deforming force is applied on it. The distance between any two given points on a rigid body rema ...
that, in normal operation, turns around a ''rotation axis'' that is fixed in space, without sliding along it. Thus, each point of the gear can move only along a circle that is perpendicular to its axis and centered on it. At any moment ''t'', all points of the gear will be rotating around that axis with the same angular speed
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine f ...
''ω''(''t''), in the same sense. The speed need not be constant over time.
The ''action surface'' of the gear consists of all points of its surface that, in normal operation, may contact the matching gear with positive pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
. All other parts of the surface are irrelevant (except that they cannot be crossed by any part of the matching gear). In a gear with ''N'' teeth, the working surface has ''N''-fold rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape (geometry), shape has when it looks the same after some rotation (mathematics), rotation by a partial turn (angle), turn. An object's degree of rotational s ...
about the axis, meaning that it is congruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
with itself when the gear rotates by of a turn.
If the gear is meant to transmit or receive torque with a definite sense only (clockwise or counterclockwise with respect to some reference viewpoint), the action surface consists of ''N'' separate patches, the ''tooth faces''; which have the same shape and are positioned in the same way relative to the axis, spaced turn apart.
If the torque on each gear may have both senses, the action surface will have two sets of ''N'' tooth faces; each set will be effective only while the torque has one specific sense, and the two sets can be analyzed independently of the other. However, in this case the gear usually has also "flip over" symmetry, so that the two sets of tooth faces are congruent after the gear is flipped. This arrangement ensures that the two gears are firmly locked together, at all times, with no backlash
Backlash may refer to:
Literature
* '' Backlash: The Undeclared War Against American Women'', a 1991 book by Susan Faludi
* ''Backlash'' (Star Wars novel), a 2010 novel by Aaron Allston
* Backlash (Marc Slayton), a comic book character from ...
.
During operation, each point ''p'' of each tooth face will at some moment contact a tooth face of the matching gear at some point ''q'' of one of its tooth faces. At that moment and at those points, the two faces must have the same perpendicular direction but opposite orientation. But since the two gears are rotating around different axes, the points ''p'' and ''q'' are moving along different circles; therefore, the contact cannot last more than one instant, and ''p'' will then either slide across the other face, or stop contacting it altogether.
On the other hand, at any given moment there is at least one such pair of contact points; usually more than one, even a whole line or surface of contact.
Actual gears deviate from this model in many ways: they are not perfectly rigid, their mounting does not ensure that the rotation axis will be perfectly fixed in space, the teeth may have slightly different shapes and spacing, the tooth faces are not perfectly smooth, and so on. Yet, these deviations from the ideal model can be ignored for a basic analysis of the operation of a gear set.
Relative axis position
One criterion for classifying gears is the relative position and direction of the axes or rotation of the gears that are to be meshed together.Parallel
In the most common configuration, the axes of rotation of the two gears are parallel, and usually their sizes are such that they contact near a point between the two axes. In this configuration, the two gears turn in opposite senses. Occasionally the axes are parallel but one gear is nested inside the other. In this configuration, both gears turn in the same sense. If the two gears are cut by an imaginary plane perpendicular to the axes, each section of one gear will interact only with the corresponding section of the other gear. Thus the three-dimensional gear train can be understood as a stack of gears that are flat and infinitesimally thin — that is, essentially two-dimensional.Crossed
In a ''crossed'' arrangement, the axes of rotation of the two gears are not parallel but cross at an arbitrary angle except zero or 180 degrees. For best operation, each wheel then must be a bevel gear, whose overall shape is like a slice ( frustum) of acone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''.
A cone is formed by a set of line segments, half-lines ...
whose apex is the meeting point of the two axes.
Bevel gears with equal numbers of teeth and shaft axes at 90 degrees are called ''miter'' (US) or ''mitre'' (UK) gears.
Independently of the angle between the axes, the larger of two unequal matching bevel gears may be internal or external, depending the desired relative sense of rotation.
If the two gears are sliced by an imaginary sphere whose center is the point where the two axes cross, each section will remain on the surface of that sphere as the gear rotates, and the section of one gear will interact only with the corresponding section of the other gear. In this way, a pair of meshed 3D gears can be understood as a stack of nested infinitely thin cup-like gears.
Skew
 The gears in a matching pair are said to be ''skew'' if their axes of rotation are skew lines -- neither parallel nor intersecting.
In this case, the best shape for each pitch surface is neither cylindrical nor conical but a portion of a
The gears in a matching pair are said to be ''skew'' if their axes of rotation are skew lines -- neither parallel nor intersecting.
In this case, the best shape for each pitch surface is neither cylindrical nor conical but a portion of a hyperboloid
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by def ...
of revolution. Such gears are called '' hypoid'' for short. Hypoid gears are most commonly found with shafts at 90 degrees.
Contact between hypoid gear teeth may be even smoother and more gradual than with spiral bevel gear teeth, but also have a sliding action along the meshing teeth as it rotates and therefore usually require some of the most viscous types of gear oil to avoid it being extruded from the mating tooth faces, the oil is normally designated HP (for hypoid) followed by a number denoting the viscosity. Also, the pinion can be designed with fewer teeth than a spiral bevel pinion, with the result that gear ratios of 60:1 and higher are feasible using a single set of hypoid gears.. This style of gear is most common in motor vehicle drive trains, in concert with a differential. Whereas a regular (nonhypoid) ring-and-pinion gear set is suitable for many applications, it is not ideal for vehicle drive trains because it generates more noise and vibration than a hypoid does. Bringing hypoid gears to market for mass-production applications was an engineering improvement of the 1920s.
Tooth orientation
Internal and external

 A gear is said to be ''external'' if its teeth are directed generally away from the rotation axis, and ''internal'' otherwise. In a pair of matching wheels, only one of them (the larger one) may be internal.
A gear is said to be ''external'' if its teeth are directed generally away from the rotation axis, and ''internal'' otherwise. In a pair of matching wheels, only one of them (the larger one) may be internal.Crown
A '' crown gear'' or ''contrate gear'' is one whose teeth project at right angles to the plane. A crown gear is also sometimes meshed with anescapement
An escapement is a mechanical linkage in mechanical watches and clocks that gives impulses to the timekeeping element and periodically releases the gear train to move forward, advancing the clock's hands. The impulse action transfers energy to t ...
such as found in mechanical clocks.
Tooth cut direction
Gear teeth typically extend across the whole thickness of the gear. Another criterion for classifying gears is the general direction of the teeth across that dimension. This attribute is affected by the relative position and direction of the axes or rotation of the gears that are to be meshed together.Straight
In a cylindrical '' spur gear'' or ''straight-cut gear'', the tooth faces are straight along the direction parallel to the axis of rotation. Any imaginary cylinder with the same axis will cut the teeth along parallel straight lines. The teeth can be either internal or external. Two spur gears mesh together correctly only if fitted to parallel shafts. No axial thrust is created by the tooth loads. Spur gears are excellent at moderate speeds but tend to be noisy at high speeds. For arrangements with crossed non-parallel axes, the faces in a straight-cut gear are parts of a general conical surface whose generating lines (''generatrices'') go through the meeting point of the two axes, resulting in a bevel gear. Such gears are generally used only at speeds below , or, for small gears, 1000rpm
Revolutions per minute (abbreviated rpm, RPM, rev/min, r/min, or r⋅min−1) is a unit of rotational speed (or rotational frequency) for rotating machines.
One revolution per minute is equivalent to hertz.
Standards
ISO 80000-3:2019 def ...
..
Helical
 In a ''helical'' or ''dry fixed'' gear the tooth walls are not parallel to the axis of rotation, but are set at an angle. An imaginary pitch surface (cylinder, cone, or hyperboloid, depending on the relative axis positions) intersects each tooth face along an arc of a
In a ''helical'' or ''dry fixed'' gear the tooth walls are not parallel to the axis of rotation, but are set at an angle. An imaginary pitch surface (cylinder, cone, or hyperboloid, depending on the relative axis positions) intersects each tooth face along an arc of a helix
A helix (; ) is a shape like a cylindrical coil spring or the thread of a machine screw. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is for ...
. Helical gears can be meshed in either ''parallel'' or ''crossed'' orientations. The former refers to when the shafts are parallel to each other; this is the most common orientation. In the latter, the shafts are non-parallel, and in this configuration the gears are sometimes known as "skew gears".
 The angled teeth engage more gradually than do spur gear teeth, causing them to run more smoothly and quietly. With parallel helical gears, each pair of teeth first make contact at a single point at one side of the gear wheel; a moving curve of contact then grows gradually across the tooth face to a maximum, then recedes until the teeth break contact at a single point on the opposite side. In spur gears, teeth suddenly meet at a line contact across their entire width, causing stress and noise. Spur gears make a characteristic whine at high speeds. For this reason spur gears are used in low-speed applications and in situations where noise control is not a problem, and helical gears are used in high-speed applications, large power transmission, or where noise abatement is important. The speed is considered high when the pitch line velocity exceeds 25 m/s.
A disadvantage of helical gears is a resultant
The angled teeth engage more gradually than do spur gear teeth, causing them to run more smoothly and quietly. With parallel helical gears, each pair of teeth first make contact at a single point at one side of the gear wheel; a moving curve of contact then grows gradually across the tooth face to a maximum, then recedes until the teeth break contact at a single point on the opposite side. In spur gears, teeth suddenly meet at a line contact across their entire width, causing stress and noise. Spur gears make a characteristic whine at high speeds. For this reason spur gears are used in low-speed applications and in situations where noise control is not a problem, and helical gears are used in high-speed applications, large power transmission, or where noise abatement is important. The speed is considered high when the pitch line velocity exceeds 25 m/s.
A disadvantage of helical gears is a resultant thrust
Thrust is a reaction force described quantitatively by Newton's third law. When a system expels or accelerates mass in one direction, the accelerated mass will cause a force of equal magnitude but opposite direction to be applied to that ...
along the axis of the gear, which must be accommodated by appropriate thrust bearing
A thrust bearing is a particular type of rotary bearing. Like other bearings they permanently rotate between parts, but they are designed to support a predominantly axial load.
Thrust bearings come in several varieties.
*''Thrust ball bearing ...
s. However, this issue can be circumvented by using a herringbone gear or ''double helical gear'', which has no axial thrust - and also provides self-aligning of the gears. This results in less axial thrust than a comparable spur gear.
A second disadvantage of helical gears is a greater degree of sliding friction between the meshing teeth, often addressed with additives in the lubricant.
For a "crossed" or "skew" configuration, the gears must have the same pressure angle and normal pitch; however, the helix angle and handedness can be different. The relationship between the two shafts is actually defined by the helix angle(s) of the two shafts and the handedness, as defined:
: for gears of the same handedness,
: for gears of opposite handedness,
where is the helix angle for the gear. The crossed configuration is less mechanically sound because there is only a point contact between the gears, whereas in the parallel configuration there is a line contact.
Quite commonly, helical gears are used with the helix angle of one having the negative of the helix angle of the other; such a pair might also be referred to as having a right-handed helix and a left-handed helix of equal angles. The two equal but opposite angles add to zero: the angle between shafts is zero—that is, the shafts are ''parallel''. Where the sum or the difference (as described in the equations above) is not zero, the shafts are ''crossed''. For shafts ''crossed'' at right angles, the helix angles are of the same hand because they must add to 90 degrees. (This is the case with the gears in the illustration above: they mesh correctly in the crossed configuration: for the parallel configuration, one of the helix angles should be reversed. The gears illustrated cannot mesh with the shafts parallel.)
3D animation of helical gears (parallel axis)
3D animation of helical gears (crossed axis)
Double helical
Double helical gears overcome the problem of axial thrust presented by single helical gears by using a double set of teeth, slanted in opposite directions. A double helical gear can be thought of as two mirrored helical gears mounted closely together on a common axle. This arrangement cancels out the net axial thrust, since each half of the gear thrusts in the opposite direction, resulting in a net axial force of zero. This arrangement can also remove the need for thrust bearings. However, double helical gears are more difficult to manufacture due to their more complicated shape. Herringbone gears are a special type of helical gears. They do not have a groove in the middle like some other double helical gears do; the two mirrored helical gears are joined so that their teeth form a V shape. This can also be applied to bevel gears, as in the final drive of the Citroën Type A. Another type of double helical gear is a Wüst gear. For both possible rotational directions, there exist two possible arrangements for the oppositely-oriented helical gears or gear faces. One arrangement is called stable, and the other unstable. In a stable arrangement, the helical gear faces are oriented so that each axial force is directed toward the center of the gear. In an unstable arrangement, both axial forces are directed away from the center of the gear. In either arrangement, the total (or ''net'') axial force on each gear is zero when the gears are aligned correctly. If the gears become misaligned in the axial direction, the unstable arrangement generates a net force that may lead to disassembly of the gear train, while the stable arrangement generates a net corrective force. If the direction of rotation is reversed, the direction of the axial thrusts is also reversed, so a stable configuration becomes unstable, and vice versa. Stable double helical gears can be directly interchanged with spur gears without any need for different bearings.Worm

 ''Worms'' resemble
''Worms'' resemble screw
A screw is an externally helical threaded fastener capable of being tightened or released by a twisting force (torque) to the screw head, head. The most common uses of screws are to hold objects together and there are many forms for a variety ...
s. A worm is meshed with a ''worm wheel'', which looks similar to a spur gear.
Worm-and-gear sets are a simple and compact way to achieve a high torque, low speed gear ratio. For example, helical gears are normally limited to gear ratios of less than 10:1 while worm-and-gear sets vary from 10:1 to 500:1.. A disadvantage is the potential for considerable sliding action, leading to low efficiency.
A worm gear is a species of helical gear, but its helix angle is usually somewhat large (close to 90 degrees) and its body is usually fairly long in the axial direction. These attributes give it screw like qualities. The distinction between a worm and a helical gear is that at least one tooth persists for a full rotation around the helix. If this occurs, it is a 'worm'; if not, it is a 'helical gear'. A worm may have as few as one tooth. If that tooth persists for several turns around the helix, the worm appears, superficially, to have more than one tooth, but what one in fact sees is the same tooth reappearing at intervals along the length of the worm. The usual screw nomenclature applies: a one-toothed worm is called ''single thread'' or ''single start''; a worm with more than one tooth is called ''multiple thread'' or ''multiple start''. The helix angle of a worm is not usually specified. Instead, the lead angle, which is equal to 90 degrees minus the helix angle, is given.
In a worm-and-gear set, the worm can always drive the gear. However, if the gear attempts to drive the worm, it may or may not succeed. Particularly if the lead angle is small, the gear's teeth may simply lock against the worm's teeth, because the force component circumferential to the worm is not sufficient to overcome friction. In traditional music box
A music box (American English) or musical box (British English) is an automatic musical instrument in a box that produces Musical note, musical notes by using a set of pins placed on a revolving cylinder (geometry), cylinder or disc to pluck ...
es, however, the gear drives the worm, which has a large helix angle. This mesh drives the speed-limiter vanes which are mounted on the worm shaft.
Worm-and-gear sets that do lock are called self locking, which can be used to advantage, as when it is desired to set the position of a mechanism by turning the worm and then have the mechanism hold that position. An example is the machine head found on some types of stringed instrument
In musical instrument classification, string instruments, or chordophones, are musical instruments that produce sound from vibrating strings when a performer strums, plucks, strikes or sounds the strings in varying manners.
Musicians play so ...
s.
If the gear in a worm-and-gear set is an ordinary helical gear only a single point of contact is achieved.. If medium to high power transmission is desired, the tooth shape of the gear is modified to achieve more intimate contact by making both gears partially envelop each other. This is done by making both concave and joining them at a saddle point
In mathematics, a saddle point or minimax point is a Point (geometry), point on the surface (mathematics), surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a Critical point (mathematics), ...
; this is called a cone-drive or "Double enveloping".
Worm gears can be right or left-handed, following the long-established practice for screw threads.
Tooth profile
 Another criterion to classify gears is the ''tooth profile'', the shape of the cross-section of a tooth face by an imaginary cut perpendicular to the pitch surface, such as the transverse, normal, or axial plane.
The tooth profile is crucial for the smoothness and uniformity of the movement of matching gears, as well as for the
Another criterion to classify gears is the ''tooth profile'', the shape of the cross-section of a tooth face by an imaginary cut perpendicular to the pitch surface, such as the transverse, normal, or axial plane.
The tooth profile is crucial for the smoothness and uniformity of the movement of matching gears, as well as for the friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
and wear.
Artisanal
 The teeth of antique or artisanal gears that were cut by hand from sheet material, like those in the Antikhytera mechanism, generally had simple profiles, such as triangles.
The teeth of larger gears — such as used in windmills — were usually pegs with simple shapes like cylinders,
The teeth of antique or artisanal gears that were cut by hand from sheet material, like those in the Antikhytera mechanism, generally had simple profiles, such as triangles.
The teeth of larger gears — such as used in windmills — were usually pegs with simple shapes like cylinders, parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square.
Three equiva ...
s, or triangular prisms inserted into a smooth wooden or metal wheel; or were holes with equally simple shapes cut into such a wheel.
Because of their sub-optimal profile, the effective gear ratio of such artisanal matching gears was not constant, but fluctuated over each tooth cycle, resulting in vibrations, noise, and accelerated wear.
Cage
 A ''cage gear'', also called a ''lantern gear'' or ''lantern pinion'', is one of those artisanal gears having cylindrical rods for teeth, parallel to the axle and arranged in a circle around it, much as the bars on a round bird cage or lantern. The assembly is held together by disks at each end, into which the tooth rods and axle are set. Cage gears are more efficient than solid pinions, and dirt can fall through the rods rather than becoming trapped and increasing wear. They can be constructed with very simple tools as the teeth are not formed by cutting or milling, but rather by drilling holes and inserting rods.
Sometimes used in clocks, a cage gear should always be driven by a gearwheel, not used as the driver. The cage gear was not initially favoured by conservative clock makers. It became popular in turret clocks where dirty working conditions were most commonplace. Domestic American clock movements often used them.
A ''cage gear'', also called a ''lantern gear'' or ''lantern pinion'', is one of those artisanal gears having cylindrical rods for teeth, parallel to the axle and arranged in a circle around it, much as the bars on a round bird cage or lantern. The assembly is held together by disks at each end, into which the tooth rods and axle are set. Cage gears are more efficient than solid pinions, and dirt can fall through the rods rather than becoming trapped and increasing wear. They can be constructed with very simple tools as the teeth are not formed by cutting or milling, but rather by drilling holes and inserting rods.
Sometimes used in clocks, a cage gear should always be driven by a gearwheel, not used as the driver. The cage gear was not initially favoured by conservative clock makers. It became popular in turret clocks where dirty working conditions were most commonplace. Domestic American clock movements often used them.
Mathematical
In most modern gears, the tooth profile is usually not straight or circular, but of special form designed to achieve a constant angular velocity ratio. There is an infinite variety of tooth profiles that will achieve this goal. In fact, given a fairly arbitrary tooth shape, it is possible to develop a tooth profile for the mating gear that will do it.Parallel and crossed axes
However, two constant velocity tooth profiles are the most commonly used in modern times for gears with parallel or crossed axes, based on the ''cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve g ...
'' and ''involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the Locus (mathematics), locus of a point on a piece of taut string as the string is eith ...
'' curves.
Cycloidal gears were more common until the late 1800s. Since then, the involute has largely superseded it, particularly in drive train applications. The cycloid is in some ways the more interesting and flexible shape; however the involute has two advantages: it is easier to manufacture, and it permits the center-to-center spacing of the gears to vary over some range without ruining the constancy of the velocity ratio. Cycloidal gears only work properly if the center spacing is exactly right. Cycloidal gears are still commonly used in mechanical clocks.
Skew axes
milling machine
Milling is the process of machining using rotary cutters to remove material by advancing a cutter into a workpiece. This may be done by varying directions on one or several axes, cutter head speed, and pressure. Milling covers a wide variety of ...
.
Spiral bevel gears have the same advantages and disadvantages relative to their straight-cut cousins as helical gears do to spur gears, such as lower noise and vibration.. Simplified calculated bevel gears on the basis of an equivalent cylindrical gear in normal section with an involute tooth form show a deviant tooth form with reduced tooth strength by 10-28% without offset and 45% with offset.
Special gear trains
Rack and pinion
 A ''rack'' is a toothed bar or rod that can be thought of as a sector gear with an infinitely large
A ''rack'' is a toothed bar or rod that can be thought of as a sector gear with an infinitely large radius of curvature
In differential geometry, the radius of curvature, , is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius ...
. Torque
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. Wh ...
can be converted to linear force by meshing a rack with a round gear called a ''pinion'': the pinion turns, while the rack moves in a straight line. Such a mechanism is used in the steering of automobiles to convert the rotation of the steering wheel
A steering wheel (also called a driving wheel, a hand wheel, or simply wheel) is a type of steering control in vehicles.
Steering wheels are used in most modern land vehicles, including all mass-production automobiles, buses, light and hea ...
into the left-to-right motion of the tie rod(s) that are attached to the front wheels.
Racks also feature in the theory of gear geometry, where, for instance, the tooth shape of an interchangeable set of gears may be specified for the rack (infinite radius), and the tooth shapes for gears of particular actual radii are then derived from that. The rack and pinion gear type is also used in a rack railway.
Epicyclic gear train
 In epicyclic gearing, one or more of the gear
In epicyclic gearing, one or more of the gear axes
Axes, plural of ''axe'' and of ''axis'', may refer to
* ''Axes'' (album), a 2005 rock album by the British band Electrelane
* a possibly still empty plot (graphics)
See also
* Axis (disambiguation)
An axis (: axes) may refer to:
Mathematics ...
moves. Examples are sun and planet gear
The sun and planet gear is a method of converting reciprocating motion to rotary motion and was used in the first rotative beam engines.
It was invented by the Scotland, Scottish engineer William Murdoch, an employee of Boulton and Watt, but wa ...
ing (see below), cycloidal drive, automatic transmission
An automatic transmission (AT) or automatic gearbox is a multi-speed transmission (mechanics), transmission used in motor vehicles that does not require any input from the driver to change forward gears under normal driving conditions.
The 1904 ...
s, and mechanical differentials.
Sun and planet

Sun and planet gear
The sun and planet gear is a method of converting reciprocating motion to rotary motion and was used in the first rotative beam engines.
It was invented by the Scotland, Scottish engineer William Murdoch, an employee of Boulton and Watt, but wa ...
ing is a method of converting reciprocating motion
Reciprocating motion, also called reciprocation, is a repetitive up-and-down or back-and-forth linear motion. It is found in a wide range of mechanisms, including reciprocating engines and pumps. The two opposite motions that comprise a single ...
into rotary motion
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersec ...
that was used in steam engine
A steam engine is a heat engine that performs Work (physics), mechanical work using steam as its working fluid. The steam engine uses the force produced by steam pressure to push a piston back and forth inside a Cylinder (locomotive), cyl ...
s. James Watt
James Watt (; 30 January 1736 (19 January 1736 OS) – 25 August 1819) was a Scottish inventor, mechanical engineer, and chemist who improved on Thomas Newcomen's 1712 Newcomen steam engine with his Watt steam engine in 1776, which was f ...
used it on his early steam engines to get around the patent on the crank, but it also provided the advantage of increasing the flywheel speed so Watt could use a lighter flywheel.
In the illustration, the sun is yellow, the planet red, the reciprocating arm is blue, the flywheel
A flywheel is a mechanical device that uses the conservation of angular momentum to store rotational energy, a form of kinetic energy proportional to the product of its moment of inertia and the square of its rotational speed. In particular, a ...
is green and the driveshaft
A drive shaft, driveshaft, driving shaft, tailshaft (Australian English), propeller shaft (prop shaft), or Cardan shaft (after Girolamo Cardano) is a component for transmitting mechanical power, torque, and rotation, usually used to connect ...
is gray.
Non-circular gears
efficiency
Efficiency is the often measurable ability to avoid making mistakes or wasting materials, energy, efforts, money, and time while performing a task. In a more general sense, it is the ability to do things well, successfully, and without waste.
...
, a non-circular gear's main objective might be ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
variations, axle displacement oscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
s and more. Common applications include textile machines, potentiometer
A potentiometer is a three- terminal resistor with a sliding or rotating contact that forms an adjustable voltage divider. If only two terminals are used, one end and the wiper, it acts as a variable resistor or rheostat.
The measuring instrum ...
s and continuously variable transmission
A continuously variable transmission (CVT) is an automated Transmission (mechanical device), transmission that can change through a continuous range of gear ratios, typically resulting in better fuel economy in gasoline applications. This contr ...
s.
Non-rigid gears
Most gears are ideally rigid bodies which transmit torque and movement through the lever principle and contact forces between the teeth. Namely, the torque applied to one gear causes it to rotate as rigid body, so that its teeth push against those of the matched gear, which in turn rotates as a rigid body transmitting the torque to its axle. Some specialized gear escape this pattern, however.Harmonic gear
 A ''harmonic gear'' or '' strain wave gear'' is a specialized gearing mechanism often used in industrial
A ''harmonic gear'' or '' strain wave gear'' is a specialized gearing mechanism often used in industrial motion control
Motion control is a sub-field of automation, encompassing the systems or sub-systems involved in moving parts of machines in a controlled manner. Motion control systems are extensively used in a variety of fields for automation purposes, includi ...
, robotics
Robotics is the interdisciplinary study and practice of the design, construction, operation, and use of robots.
Within mechanical engineering, robotics is the design and construction of the physical structures of robots, while in computer s ...
and aerospace
Aerospace is a term used to collectively refer to the atmosphere and outer space. Aerospace activity is very diverse, with a multitude of commercial, industrial, and military applications. Aerospace engineering consists of aeronautics and astron ...
for its advantages over traditional gearing systems, including lack of backlash, compactness and high gear ratios.
Though the diagram does not demonstrate the correct configuration, it is a "timing gear," conventionally with far more teeth than a traditional gear to ensure a higher degree of precision.
Magnetic gear
In a ''magnetic gear'' pair there is no contact between the two members; the torque is instead transmitted through magnetic fields. The cogs of each gear are constantmagnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, steel, nickel, ...
s with periodic alternation of opposite magnetic poles on mating surfaces. Gear components are mounted with a backlash
Backlash may refer to:
Literature
* '' Backlash: The Undeclared War Against American Women'', a 1991 book by Susan Faludi
* ''Backlash'' (Star Wars novel), a 2010 novel by Aaron Allston
* Backlash (Marc Slayton), a comic book character from ...
capability similar to other mechanical gearings. Although they cannot exert as much force as a traditional gear due to limits on magnetic field strength, such gears work without touching and so are immune to wear, have very low noise, minimal power losses from friction and can slip without damage making them very reliable. They can be used in configurations that are not possible for gears that must be physically touching and can operate with a non-metallic barrier completely separating the driving force from the load. The magnetic coupling A magnetic coupling is a component which transfers torque from one shaft to another using a magnetic field, rather than a physical mechanical connection. They are also known as magnetic drive couplings, magnetic shaft couplings, or magnetic disc co ...
can transmit force into a hermetically sealed
A hermetic seal is any type of sealing that makes a given object airtight (preventing the passage of air, oxygen, or other gases). The term originally applied to airtight glass containers but, as technology advanced, it applied to a larger ca ...
enclosure without using a radial shaft seal, which may leak. Magnetic gears are also used in brushless motors along with electromagnets to make the motor spin.
Nomenclature
General
 ; Rotational
; Rotational frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
, ''n'' : Measured in rotation over time, such as revolutions per minute
Revolutions per minute (abbreviated rpm, RPM, rev/min, r/min, or r⋅min−1) is a unit of rotational speed (or rotational frequency) for rotating machines.
One revolution per minute is equivalent to hertz.
Standards
ISO 80000-3:2019 de ...
(RPM or rpm).
; Angular frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine ...
, ''ω'' : Measured in radians per second. 1RPM = 2rad/minute = rad/second.
; Number of teeth, ''N'' : How many teeth a gear has, an integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
. In the case of worms, it is the number of thread starts that the worm has.
; Gear, wheel : The larger of two interacting gears or a gear on its own.
; Pinion : The smaller of two interacting gears.
; Path of contact : Path followed by the point of contact between two meshing gear teeth.
; Line of action, pressure line : Line along which the force between two meshing gear teeth is directed. It has the same direction as the force vector. In general, the line of action changes from moment to moment during the period of engagement of a pair of teeth. For involute gears, however, the tooth-to-tooth force is always directed along the same line—that is, the line of action is constant. This implies that for involute gears the path of contact is also a straight line, coincident with the line of action—as is indeed the case.
; Axis : Axis of revolution of the gear; center line of the shaft.
; Pitch point : Point where the line of action crosses a line joining the two gear axes.
; Pitch circle, pitch line : Circle centered on and perpendicular to the axis, and passing through the pitch point. A predefined diametral position on the gear where the circular tooth thickness, pressure angle and helix angles are defined.
; Pitch diameter, ''d'': A predefined diametral position on the gear where the circular tooth thickness, pressure angle and helix angles are defined. The standard pitch diameter is a design dimension and cannot be measured, but is a location where other measurements are made. Its value is based on the number of teeth (''N''), the normal module (''mn''; or normal diametral pitch, ''Pd''), and the helix angle ():
:: in metric units or in imperial units.ISO/DIS 21771:2007 : "Gears – Cylindrical Involute Gears and Gear Pairs – Concepts and Geometry", ''International Organization for Standardization'', (2007)
; Module or modulus, ''m'': Since it is impractical to calculate circular pitch with irrational number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, ...
s, mechanical engineers usually use a scaling factor that replaces it with a regular value instead. This is known as the ''module'' or ''modulus'' of the wheel and is simply defined as:
::
: where ''m'' is the module and ''p'' the circular pitch. The units
Unit may refer to:
General measurement
* Unit of measurement, a definite magnitude of a physical quantity, defined and adopted by convention or by law
**International System of Units (SI), modern form of the metric system
**English units, histo ...
of module are customarily millimeters; an ''English Module'' is sometimes used with the units of inches
The inch (symbol: in or ) is a unit of length in the British Imperial and the United States customary systems of measurement. It is equal to yard or of a foot. Derived from the Roman uncia ("twelfth"), the word ''inch'' is also sometim ...
. When the diametral pitch, DP, is in English units,
:: in conventional metric units.
: The distance between the two axis becomes:
::
: where a is the axis distance, ''z''1 and ''z''2 are the number of cogs (teeth) for each of the two wheels (gears). These numbers (or at least one of them) is often chosen among primes to create an even contact between every cog of both wheels, and thereby avoid unnecessary wear and damage. An even uniform gear wear is achieved by ensuring the tooth counts of the two gears meshing together are relatively prime
In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equiv ...
to each other; this occurs when the greatest common divisor (GCD) of each gear tooth count equals 1, e.g. GCD(16,25)=1; if a 1:1 gear ratio is desired a relatively prime gear may be inserted in between the two gears; this maintains the 1:1 ratio but reverses the gear direction; a second relatively prime gear could also be inserted to restore the original rotational direction while maintaining uniform wear with all 4 gears in this case. Mechanical engineers, at least in continental Europe, usually use the module instead of circular pitch. The module, just like the circular pitch, can be used for all types of cogs, not just evolvent based straight cogs.
; Operating pitch diameters : Diameters determined from the number of teeth and the center distance at which gears operate. Example for pinion:
::
; Pitch surface : In cylindrical gears, cylinder formed by projecting a pitch circle in the axial direction. More generally, the surface formed by the sum of all the pitch circles as one moves along the axis. For bevel gears it is a cone.
; Angle of action : Angle with vertex at the gear center, one leg on the point where mating teeth first make contact, the other leg on the point where they disengage.
; Arc of action : Segment of a pitch circle subtended by the angle of action.
; Pressure angle, ''θ'' : The complement of the angle between the direction that the teeth exert force on each other, and the line joining the centers of the two gears. For involute gears, the teeth always exert force along the line of action, which, for involute gears, is a straight line; and thus, for involute gears, the pressure angle is constant.
; Outside diameter, ''Do'' : Diameter of the gear, measured from the tops of the teeth.
; Root diameter : Diameter of the gear, measured at the base of the tooth.
; Addendum, ''a'' : Radial distance from the pitch surface to the outermost point of the tooth.
; Dedendum, ''b'' : Radial distance from the depth of the tooth trough to the pitch surface.
; Whole depth, ''ht'' : The distance from the top of the tooth to the root; it is equal to addendum plus dedendum or to working depth plus clearance.
; Clearance : Distance between the root circle of a gear and the addendum circle of its mate.
; Working depth : Depth of engagement of two gears, that is, the sum of their operating addendums.
; Circular pitch, ''p'' : Distance from one face of a tooth to the corresponding face of an adjacent tooth on the same gear, measured along the pitch circle.
; Diametral pitch, ''DP'' :
::
: Ratio of the number of teeth to the pitch diameter. Could be measured in teeth per inch or teeth per centimeter, but conventionally has units of per inch of diameter. Where the module, ''m'', is in metric units
:: in imperial units
; Base circle : In involute gears, the tooth profile is generated by the involute of the base circle. The radius of the base circle is somewhat smaller than that of the pitch circle
; Base pitch, normal pitch, ''pb'' : In involute gears, distance from one face of a tooth to the corresponding face of an adjacent tooth on the same gear, measured along the base circle
; Interference : Contact between teeth other than at the intended parts of their surfaces
; Interchangeable set : A set of gears, any of which mates properly with any other
Helical gear
; Helix angle, ''ψ'' : the Angle between a tangent to the helix and the gear axis. It is zero in the limiting case of a spur gear, albeit it can be considered as the hypotenuse angle as well. ; Normal circular pitch, ''pn'' : Circular pitch in the plane normal to the teeth. ; Transverse circular pitch, ''p'' : Circular pitch in the plane of rotation of the gear. Sometimes just called "circular pitch". :: Several other helix parameters can be viewed either in the normal or transverse planes. The subscript ''n'' usually indicates the normal.Worm gear
; Lead : Distance from any point on a thread to the corresponding point on the next turn of the same thread, measured parallel to the axis. ; Linear pitch, ''p'' : Distance from any point on a thread to the corresponding point on the adjacent thread, measured parallel to the axis. For a single-thread worm, lead and linear pitch are the same. ; Lead angle, ''λ'' : Angle between a tangent to the helix and a plane perpendicular to the axis. Note that the complement of the helix angle is usually given for helical gears. ; Pitch diameter, ''dw'' : Same as described earlier in this list. Note that for a worm it is still measured in a plane perpendicular to the gear axis, not a tilted plane. Subscript ''w'' denotes the worm, subscript ''g'' denotes the gear.Tooth contact
Tooth thickness
Pitch
Pitch is the distance between a point on one tooth and the corresponding point on an adjacent tooth. It is a dimension measured along a line or curve in the transverse, normal, or axial directions. The use of the single word ''pitch'' without qualification may be ambiguous, and for this reason it is preferable to use specific designations such as transverse circular pitch, normal base pitch, axial pitch.Backlash
Backlash
Backlash may refer to:
Literature
* '' Backlash: The Undeclared War Against American Women'', a 1991 book by Susan Faludi
* ''Backlash'' (Star Wars novel), a 2010 novel by Aaron Allston
* Backlash (Marc Slayton), a comic book character from ...
is the error in motion that occurs when gears change direction. It exists because there is always some gap between the trailing face of the driving tooth and the leading face of the tooth behind it on the driven gear, and that gap must be closed before force can be transferred in the new direction. The term "backlash" can also be used to refer to the size of the gap, not just the phenomenon it causes; thus, one could speak of a pair of gears as having, for example, "0.1 mm of backlash." A pair of gears could be designed to have zero backlash, but this would presuppose perfection in manufacturing, uniform thermal expansion characteristics throughout the system, and no lubricant. Therefore, gear pairs are designed to have some backlash. It is usually provided by reducing the tooth thickness of each gear by half the desired gap distance. In the case of a large gear and a small pinion, however, the backlash is usually taken entirely off the gear and the pinion is given full sized teeth. Backlash can also be provided by moving the gears further apart. The backlash of a gear train
A gear train or gear set is a machine element of a mechanical system formed by mounting two or more gears on a frame such that the teeth of the gears engage.
Gear teeth are designed to ensure the pitch circles of engaging gears roll on each oth ...
equals the sum of the backlash of each pair of gears, so in long trains backlash can become a problem.
For situations that require precision, such as instrumentation and control, backlash can be minimized through one of several techniques. For instance, the gear can be split along a plane perpendicular to the axis, one half fixed to the shaft in the usual manner, the other half placed alongside it, free to rotate about the shaft, but with springs between the two-halves providing relative torque between them, so that one achieves, in effect, a single gear with expanding teeth. Another method involves tapering the teeth in the axial direction and letting the gear slide in the axial direction to take up slack.
Standard pitches and the module system
Although gears can be made with any pitch, for convenience and interchangeability standard pitches are frequently used. Pitch is a property associated with lineardimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
s and so differs whether the standard values are in the imperial (inch) or metric
Metric or metrical may refer to:
Measuring
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
...
systems. Using ''inch'' measurements, standard diametral pitch values with units of "per inch" are chosen; the ''diametral pitch'' is the number of teeth on a gear of one inch pitch diameter. Common standard values for spur gears are 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 48, 64, 72, 80, 96, 100, 120, and 200. Certain standard pitches such as ' and ' in inch measurements, which mesh with linear rack, are actually (linear) ''circular pitch'' values with units of "inches"
When gear dimensions are in the metric system the pitch specification is generally in terms of module or ''modulus'', which is effectively a length measurement across the ''pitch diameter''. The term module is understood to mean the pitch diameter in millimetres divided by the number of teeth. When the module is based upon inch measurements, it is known as the ''English module'' to avoid confusion with the metric module. Module is a direct dimension ("millimeters per tooth"), unlike diametral pitch, which is an inverse dimension ("teeth per inch"). Thus, if the pitch diameter of a gear is 40 mm and the number of teeth 20, the module is 2, which means that there are 2 mm of pitch diameter for each tooth. The preferred standard module values are 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8, 1.0, 1.25, 1.5, 2.0, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40 and 50.
Gear model in modern physics
Modern physics
Modern physics is a branch of physics that developed in the early 20th century and onward or branches greatly influenced by early 20th century physics. Notable branches of modern physics include quantum mechanics, special relativity, and genera ...
adopted the gear model in different ways. In the nineteenth century, James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism an ...
developed a model of electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interacti ...
in which magnetic field lines were rotating tubes of incompressible fluid. Maxwell used a gear wheel and called it an "idle wheel" to explain the electric current as a rotation of particles in opposite directions to that of the rotating field lines.
More recently, quantum physics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
uses "quantum gears" in their model. A group of gears can serve as a model for several different systems, such as an artificially constructed nanomechanical device or a group of ring molecules.
The three wave hypothesis compares the wave–particle duality
Wave–particle duality is the concept in quantum mechanics that fundamental entities of the universe, like photons and electrons, exhibit particle or wave (physics), wave properties according to the experimental circumstances. It expresses the in ...
to a bevel gear.
Gear mechanism in natural world
 The gear mechanism was previously considered exclusively artificial, but as early as 1957, gears had been recognized in the hind legs of various species of
The gear mechanism was previously considered exclusively artificial, but as early as 1957, gears had been recognized in the hind legs of various species of planthopper
A planthopper is any insect in the infraorder Fulgoromorpha, in the suborder Auchenorrhyncha, a group exceeding 12,500 described species worldwide. The name comes from their remarkable resemblance to leaves and other plants of their environment ...
s
and scientists from the University of Cambridge
The University of Cambridge is a Public university, public collegiate university, collegiate research university in Cambridge, England. Founded in 1209, the University of Cambridge is the List of oldest universities in continuous operation, wo ...
characterized their functional significance in 2013 by doing high-speed photography of the nymphs of '' Issus coleoptratus'' at Cambridge University.
These gears are found only in the nymph forms of all planthoppers, and are lost during the final molt to the adult stage. In ''I. coleoptratus'', each leg has a 400-micrometer strip of teeth, pitch radius 200 micrometers, with 10 to 12 fully interlocking spur-type gear teeth, including filleted curves at the base of each tooth to reduce the risk of shearing.
The joint rotates like mechanical gears, and synchronizes ''Issus's'' hind legs when it jumps to within 30 microseconds, preventing yaw rotation.
The gears are not connected all the time. One is located on each of the juvenile insect's hind legs, and when it prepares to jump, the two sets of teeth lock together. As a result, the legs move in almost perfect unison, giving the insect more power as the gears rotate to their stopping point and then unlock.
See also
* Gear box *Sprocket
A sprocket, sprocket-wheel or chainwheel is a profiled wheel
A wheel is a rotating component (typically circular in shape) that is intended to turn on an axle Bearing (mechanical), bearing. The wheel is one of the key components of the whe ...
* Chain reaction
A chain reaction is a sequence of reactions where a reactive product or by-product causes additional reactions to take place. In a chain reaction, positive feedback leads to a self-amplifying chain of events.
Chain reactions are one way that sys ...
* Differential
* Superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So th ...
* Kinematic chain
References
Bibliography * * * * Industrial Press (2012), Machinery's Handbook (29th ed.), *Further reading
* * * * Kravchenko A.I., Bovda A.M. Gear with magnetic couple. Pat. of Ukraine N. 56700 – Bul. N. 2, 2011 – F16H 49/00. * Sclater, Neil. (2011). "Gears: devices, drives and mechanisms." ''Mechanisms and Mechanical Devices Sourcebook.'' 5th ed. New York: McGraw Hill. pp. 131–174. . Drawings and designs of various gearings."Wheels That Can't Slip."
''Popular Science'', February 1945, pp. 120–125.
External links
Geararium. Museum of gears and toothed wheels
- antique and vintage gears, sprockets, ratchets and other gear-related objects.
Kinematic Models for Design Digital Library (KMODDL)
- movies and photos of hundreds of working models at Cornell University
Short historical account on the application of analytical geometry to the form of gear teeth
{{Kinematic pair Tribology Articles containing video clips