

In
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a manifold is a
topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
that locally resembles
Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
near each point. More precisely, an
-dimensional manifold, or ''
-manifold'' for short, is a topological space with the property that each point has a
neighborhood
A neighbourhood (Commonwealth English) or neighborhood (American English) is a geographically localized community within a larger town, city, suburb or rural area, sometimes consisting of a single street and the buildings lining it. Neigh ...
that is
homeomorphic to an
open subset of
-dimensional Euclidean space.
One-dimensional manifolds include
lines and
circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
s, but not
self-crossing curves such as a figure 8. Two-dimensional manifolds are also called
surfaces. Examples include the
plane, the
sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
, and the
torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
, and also the
Klein bottle
In mathematics, the Klein bottle () is an example of a Orientability, non-orientable Surface (topology), surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the ...
and
real projective plane.
The concept of a manifold is central to many parts of
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
and modern
mathematical physics
Mathematical physics is the development of mathematics, mathematical methods for application to problems in physics. The ''Journal of Mathematical Physics'' defines the field as "the application of mathematics to problems in physics and the de ...
because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of
systems of equations and as
graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates (e.g.
CT scan
A computed tomography scan (CT scan), formerly called computed axial tomography scan (CAT scan), is a medical imaging technique used to obtain detailed internal images of the body. The personnel that perform CT scans are called radiographers or ...
s).
Manifolds can be equipped with additional structure. One important class of manifolds are
differentiable manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One ...
s; their
differentiable structure allows
calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
to be done. A
Riemannian metric on a manifold allows
distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...
s and
angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s to be measured.
Symplectic manifolds serve as the
phase spaces in the
Hamiltonian formalism of
classical mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics inv ...
, while four-dimensional
Lorentzian manifolds model
spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
in
general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
.
The study of manifolds requires working knowledge of calculus and
topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
.
Motivating examples
Circle

After a line, a circle is the simplest example of a topological manifold. Topology ignores bending, so a small piece of a circle is treated the same as a small piece of a line. Considering, for instance, the top part of the
unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, ''x''
2 + ''y''
2 = 1, where the
''y''-coordinate is positive (indicated by the yellow arc in ''Figure 1''). Any point of this arc can be uniquely described by its ''x''-coordinate. So,
projection onto the first coordinate is a
continuous and
invertible
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that ...
mapping from the upper arc to the
open interval
In mathematics, a real interval is the set (mathematics), set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without ...
(−1, 1):
Such functions along with the open regions they map are called ''
charts''. Similarly, there are charts for the bottom (red), left (blue), and right (green) parts of the circle:
Together, these parts cover the whole circle, and the four charts form an
atlas
An atlas is a collection of maps; it is typically a bundle of world map, maps of Earth or of a continent or region of Earth. Advances in astronomy have also resulted in atlases of the celestial sphere or of other planets.
Atlases have traditio ...
for the circle.
The top and right charts,
and
respectively, overlap in their domain: their intersection lies in the quarter of the circle where both
and
-coordinates are positive. Both map this part into the interval
, though differently. Thus a function
can be constructed, which takes values from the co-domain of
back to the circle using the inverse, followed by
back to the interval. If ''a'' is any number in
, then:
Such a function is called a
''transition map''.

The top, bottom, left, and right charts do not form the only possible atlas. Charts need not be geometric projections, and the number of charts is a matter of choice. Consider the charts
and
Here ''s'' is the slope of the line through the point at coordinates (''x'', ''y'') and the fixed pivot point (−1, 0); similarly, ''t'' is the opposite of the slope of the line through the points at coordinates (''x'', ''y'') and (+1, 0). The inverse mapping from ''s'' to (''x'', ''y'') is given by
It can be confirmed that ''x''
2 + ''y''
2 = 1 for all values of ''s'' and ''t''. These two charts provide a second atlas for the circle, with the transition map
(that is, one has this relation between ''s'' and ''t'' for every point where ''s'' and ''t'' are both nonzero).
Each chart omits a single point, either (−1, 0) for ''s'' or (+1, 0) for ''t'', so neither chart alone is sufficient to cover the whole circle. It can be proved that it is not possible to cover the full circle with a single chart. For example, although it is possible to construct a circle from a single line interval by overlapping and "gluing" the ends, this does not produce a chart; a portion of the circle will be mapped to both ends at once, losing invertibility.
Sphere
The
sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
is an example of a surface. The
unit sphere of
implicit equation
:
may be covered by an atlas of six
chart
A chart (sometimes known as a graph) is a graphics, graphical representation for data visualization, in which "the data is represented by symbols, such as bars in a bar chart, lines in a line chart, or slices in a pie chart". A chart can repres ...
s: the plane divides the sphere into two half spheres ( and ), which may both be mapped on the disc by the projection on the plane of coordinates. This provides two charts; the four other charts are provided by a similar construction with the two other coordinate planes.
As with the circle, one may define one chart that covers the whole sphere excluding one point. Thus two charts are sufficient, but the sphere cannot be covered by a single chart.
This example is historically significant, as it has motivated the terminology; it became apparent that the whole surface of the
Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
cannot have a plane representation consisting of a single
map (also called "chart", see
nautical chart
A nautical chart or hydrographic chart is a graphic representation of a sea region or water body and adjacent coasts or river bank, banks. Depending on the scale (map), scale of the chart, it may show depths of water (bathymetry) and heights of ...
), and therefore one needs
atlas
An atlas is a collection of maps; it is typically a bundle of world map, maps of Earth or of a continent or region of Earth. Advances in astronomy have also resulted in atlases of the celestial sphere or of other planets.
Atlases have traditio ...
es for covering the whole Earth surface.
Other curves

Manifolds do not need to be
connected (all in "one piece"); an example is a pair of separate circles.
Manifolds need not be
closed; thus a line segment without its end points is a manifold. They are never
countable
In mathematics, a Set (mathematics), set is countable if either it is finite set, finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function fro ...
, unless the dimension of the manifold is 0. Putting these freedoms together, other examples of manifolds are a
parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
, a
hyperbola, and the
locus of points on a
cubic curve (a closed loop piece and an open, infinite piece).
However, excluded are examples like two touching circles that share a point to form a figure-8; at the shared point, a satisfactory chart cannot be created. Even with the bending allowed by topology, the vicinity of the shared point looks like a "+", not a line. A "+" is not homeomorphic to a line segment, since deleting the center point from the "+" gives a space with four
components
Component may refer to:
In engineering, science, and technology Generic systems
*System components, an entity with discrete structure, such as an assembly or software module, within a system considered at a particular level of analysis
* Lumped e ...
(i.e. pieces), whereas deleting a point from a line segment gives a space with at most two pieces;
topological operations always preserve the number of pieces.
Definition
Informally, a manifold is a
space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
that is "modeled on" Euclidean space.
A manifold can be constructed by giving a collection of coordinate charts, that is, a covering by open sets with homeomorphisms to a Euclidean space, and patching functions: homeomorphisms from one region of Euclidean space to another region if they correspond to the same part of the manifold in two different coordinate charts. A manifold can be given additional structure if the patching functions satisfy axioms beyond continuity. For instance,
differentiable manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One ...
s have homeomorphisms on overlapping neighborhoods
diffeomorphic with each other, so that the manifold has a well-defined set of functions which are differentiable in each neighborhood, thus differentiable on the manifold as a whole.
Formally, a (topological) manifold is a
second countable Hausdorff space
In topology and related branches of mathematics, a Hausdorff space ( , ), T2 space or separated space, is a topological space where distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topologi ...
that is locally homeomorphic to a Euclidean space.
''Second countable'' and ''Hausdorff'' are
point-set conditions; ''second countable'' excludes spaces which are in some sense 'too large' such as the
long line, while ''Hausdorff'' excludes spaces such as "the line with two origins" (these generalizations of manifolds are discussed in
non-Hausdorff manifolds).
''Locally homeomorphic'' to a Euclidean space means that every point has a neighborhood
homeomorphic to an
open subset of the
Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
for some nonnegative integer .
This implies that either the point is an
isolated point (if
), or it has a neighborhood homeomorphic to the
open ball
This implies also that every point has a neighborhood homeomorphic to
since
is homeomorphic, and even
diffeomorphic to any open ball in it (for
).
The that appears in the preceding definition is called the ''local dimension'' of the manifold. Generally manifolds are taken to have a constant local dimension, and the local dimension is then called the ''dimension'' of the manifold. This is, in particular, the case when manifolds are
connected. However, some authors admit manifolds that are not connected, and where different points can have different
dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
s. If a manifold has a fixed dimension, this can be emphasized by calling it a . For example, the (surface of a) sphere has a constant dimension of 2 and is therefore a pure manifold whereas the
disjoint union of a sphere and a line in three-dimensional space is ''not'' a pure manifold. Since dimension is a local invariant (i.e. the map sending each point to the dimension of its neighbourhood over which a chart is defined, is
locally constant), each
connected component has a fixed dimension.
Sheaf-theoretically, a manifold is a
locally ringed space, whose structure
sheaf is locally isomorphic to the sheaf of continuous (or differentiable, or complex-analytic, etc.) functions on Euclidean space. This definition is mostly used when discussing analytic manifolds in
algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
.
Charts, atlases, and transition maps
The spherical Earth is navigated using flat maps or charts, collected in an atlas. Similarly, a manifold can be described using
mathematical maps, called ''coordinate charts'', collected in a mathematical ''atlas''. It is not generally possible to describe a manifold with just one chart, because the global structure of the manifold is different from the simple structure of the charts. For example, no single flat map can represent the entire Earth without separation of adjacent features across the map's boundaries or duplication of coverage. When a manifold is constructed from multiple overlapping charts, the regions where they overlap carry information essential to understanding the global structure.
Charts
A ''coordinate map'', a ''coordinate chart'', or simply a ''chart'', of a manifold is an invertible map between a subset of the manifold and a simple space such that both the map and its inverse preserve the desired structure.
For a topological manifold, the simple space is a subset of some Euclidean space
and interest focuses on the topological structure. This structure is preserved by
homeomorphisms, invertible maps that are continuous in both directions.
In the case of a differentiable manifold, a set of ''charts'' called an ''atlas'', whose ''transition functions'' (see below) are all differentiable, allows us to do calculus on it.
Polar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
, for example, form a chart for the plane
minus the positive ''x''-axis and the origin. Another example of a chart is the map χ
top mentioned above, a chart for the circle.
Atlases
The description of most manifolds requires more than one chart. A specific collection of charts which covers a manifold is called an ''
atlas
An atlas is a collection of maps; it is typically a bundle of world map, maps of Earth or of a continent or region of Earth. Advances in astronomy have also resulted in atlases of the celestial sphere or of other planets.
Atlases have traditio ...
''. An atlas is not unique as all manifolds can be covered in multiple ways using different combinations of charts. Two atlases are said to be equivalent if their union is also an atlas.
The atlas containing all possible charts consistent with a given atlas is called the ''maximal atlas'' (i.e. an equivalence class containing that given atlas). Unlike an ordinary atlas, the maximal atlas of a given manifold is unique. Though useful for definitions, it is an abstract object and not used directly (e.g. in calculations).
Transition maps
Charts in an atlas may overlap and a single point of a manifold may be represented in several charts. If two charts overlap, parts of them represent the same region of the manifold, just as a map of Europe and a map of Russia may both contain Moscow. Given two overlapping charts, a ''transition function'' can be defined which goes from an open ball in
to the manifold and then back to another (or perhaps the same) open ball in
. The resultant map, like the map ''T'' in the circle example above, is called a ''change of coordinates'', a ''coordinate transformation'', a ''transition function'', or a ''transition map''.
Additional structure
An atlas can also be used to define additional structure on the manifold. The structure is first defined on each chart separately. If all transition maps are compatible with this structure, the structure transfers to the manifold.
This is the standard way differentiable manifolds are defined. If the transition functions of an atlas for a topological manifold preserve the natural differential structure of
(that is, if they are
diffeomorphisms), the differential structure transfers to the manifold and turns it into a differentiable manifold.
Complex manifold
In differential geometry and complex geometry, a complex manifold is a manifold with a ''complex structure'', that is an atlas (topology), atlas of chart (topology), charts to the open unit disc in the complex coordinate space \mathbb^n, such th ...
s are introduced in an analogous way by requiring that the transition functions of an atlas are
holomorphic function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex de ...
s. For
symplectic manifolds, the transition functions must be
symplectomorphisms.
The structure on the manifold depends on the atlas, but sometimes different atlases can be said to give rise to the same structure. Such atlases are called ''compatible''.
These notions are made precise in general through the use of
pseudogroups.
Manifold with boundary

A manifold with boundary is a manifold with an edge. For example, a
disk (circle plus interior) is a
2-manifold with as boundary the circle, a
1-manifold. The boundary of an
-manifold with boundary is an
-manifold. In three dimensions, a
ball (sphere plus interior) is a 3-manifold with boundary. Its boundary is a sphere, a 2-manifold.
In technical language, a manifold with boundary is a space containing both interior points and boundary points. Every interior point has a neighborhood homeomorphic to the open
-ball
. Every boundary point has a neighborhood homeomorphic to the "half"
-ball
. Any homeomorphism between half-balls must send points with
to points with
. This invariance allows to "define" boundary points; see next paragraph.
If in addition we are considering differentiable manifolds, then a
square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
with interior is not a manifold with boundary. The four vertices are neither locally diffeomorphic to Euclidean space nor to Euclidean half-space. This is an example of a differentiable manifold with corners. Similarly, products of differentiable manifolds with boundaries are not generally differentiable manifolds with boundaries, but instead are differentiable manifolds with corners.
Boundary and interior
Let
be a manifold with boundary. The interior of
, denoted
, is the set of points in
which have neighborhoods homeomorphic to an open subset of
. The boundary of
, denoted
, is the
complement of
in
. The boundary points can be characterized as those points which land on the boundary hyperplane
of
under some coordinate chart.
If
is a manifold with boundary of dimension
, then
is a manifold (without boundary) of dimension
and
is a manifold (without boundary) of dimension
.
Construction
A single manifold can be constructed in different ways, each stressing a different aspect of the manifold, thereby leading to a slightly different viewpoint.
Charts

Perhaps the simplest way to construct a manifold is the one used in the example above of the circle. First, a subset of
is identified, and then an atlas covering this subset is constructed. The concept of ''manifold'' grew historically from constructions like this. Here is another example, applying this method to the construction of a sphere:
Sphere with charts
A sphere can be treated in almost the same way as the circle. In mathematics a sphere is just the surface (not the solid interior), which can be defined as a subset of
:
The sphere is two-dimensional, so each chart will map part of the sphere to an open subset of
. Consider the northern hemisphere, which is the part with positive ''z'' coordinate (coloured red in the picture on the right). The function defined by
maps the northern hemisphere to the open
unit disc by projecting it on the (''x'', ''y'') plane. A similar chart exists for the southern hemisphere. Together with two charts projecting on the (''x'', ''z'') plane and two charts projecting on the (''y'', ''z'') plane, an atlas of six charts is obtained which covers the entire sphere.
This can be easily generalized to higher-dimensional spheres.
Patchwork
A manifold can be constructed by gluing together pieces in a consistent manner, making them into overlapping charts. This construction is possible for any manifold and hence it is often used as a characterisation, especially for differentiable and Riemannian manifolds. It focuses on an atlas, as the patches naturally provide charts, and since there is no exterior space involved it leads to an intrinsic view of the manifold.
The manifold is constructed by specifying an atlas, which is itself defined by transition maps. A point of the manifold is therefore an
equivalence class of points which are mapped to each other by transition maps. Charts map equivalence classes to points of a single patch. There are usually strong demands on the consistency of the transition maps. For topological manifolds they are required to be homeomorphisms; if they are also diffeomorphisms, the resulting manifold is a differentiable manifold.
This can be illustrated with the transition map ''t'' =
1⁄
''s'' from the second half of the circle example. Start with two copies of the line. Use the coordinate ''s'' for the first copy, and ''t'' for the second copy. Now, glue both copies together by identifying the point ''t'' on the second copy with the point ''s'' =
1⁄
''t'' on the first copy (the points ''t'' = 0 and ''s'' = 0 are not identified with any point on the first and second copy, respectively). This gives a circle.
Intrinsic and extrinsic view
The first construction and this construction are very similar, but represent rather different points of view. In the first construction, the manifold is seen as
embedded in some Euclidean space. This is the ''extrinsic view''. When a manifold is viewed in this way, it is easy to use intuition from Euclidean spaces to define additional structure. For example, in a Euclidean space, it is always clear whether a vector at some point is
tangential or
normal to some surface through that point.
The patchwork construction does not use any embedding, but simply views the manifold as a topological space by itself. This abstract point of view is called the ''intrinsic view''. It can make it harder to imagine what a tangent vector might be, and there is no intrinsic notion of a
normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding (or immersion).
Definition
Riemannian manifold
Let (M,g) be a Riemannian ...
, but instead there is an intrinsic
stable normal bundle.
''n''-Sphere as a patchwork
The
''n''-sphere S
''n'' is a generalisation of the idea of a circle (1-sphere) and sphere (2-sphere) to higher dimensions. An ''n''-sphere S
''n'' can be constructed by gluing together two copies of
. The transition map between them is
inversion in a sphere, defined as
This function is its own inverse and thus can be used in both directions. As the transition map is a
smooth function, this atlas defines a smooth manifold.
In the case ''n'' = 1, the example simplifies to the circle example given earlier.
Identifying points of a manifold
It is possible to define different points of a manifold to be the same point. This can be visualized as gluing these points together in a single point, forming a
quotient space. There is, however, no reason to expect such quotient spaces to be manifolds. Among the possible quotient spaces that are not necessarily manifolds,
orbifolds and
CW complex
In mathematics, and specifically in topology, a CW complex (also cellular complex or cell complex) is a topological space that is built by gluing together topological balls (so-called ''cells'') of different dimensions in specific ways. It generali ...
es are considered to be relatively
well-behaved
In mathematics, when a mathematical phenomenon runs counter to some intuition, then the phenomenon is sometimes called pathological. On the other hand, if a phenomenon does not run counter to intuition, it is sometimes called well-behaved or n ...
. An example of a quotient space of a manifold that is also a manifold is the
real projective space, identified as a quotient space of the corresponding sphere.
One method of identifying points (gluing them together) is through a right (or left) action of a
group, which
acts on the manifold. Two points are identified if one is moved onto the other by some group element. If ''M'' is the manifold and ''G'' is the group, the resulting quotient space is denoted by ''M'' / ''G'' (or ''G'' \ ''M'').
Manifolds which can be constructed by identifying points include
tori and
real projective spaces (starting with a plane and a sphere, respectively).
Gluing along boundaries
Two manifolds with boundaries can be glued together along a boundary. If this is done the right way, the result is also a manifold. Similarly, two boundaries of a single manifold can be glued together.
Formally, the gluing is defined by a
bijection
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
between the two boundaries. Two points are identified when they are mapped onto each other. For a topological manifold, this bijection should be a homeomorphism, otherwise the result will not be a topological manifold. Similarly, for a differentiable manifold, it has to be a diffeomorphism. For other manifolds, other structures should be preserved.
A finite cylinder may be constructed as a manifold by starting with a strip
,1nbsp;×
,1and gluing a pair of opposite edges on the boundary by a suitable diffeomorphism. A
projective plane may be obtained by gluing a sphere with a hole in it to a
Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
along their respective circular boundaries.
Cartesian products
The
Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets and , denoted , is the set of all ordered pairs where is an element of and is an element of . In terms of set-builder notation, that is
A\times B = \.
A table c ...
of manifolds is also a manifold.
The dimension of the product manifold is the sum of the dimensions of its factors. Its topology is the
product topology
In topology and related areas of mathematics, a product space is the Cartesian product of a family of topological spaces equipped with a natural topology called the product topology. This topology differs from another, perhaps more natural-seemin ...
, and a Cartesian product of charts is a chart for the product manifold. Thus, an atlas for the product manifold can be constructed using atlases for its factors. If these atlases define a differential structure on the factors, the corresponding atlas defines a differential structure on the product manifold. The same is true for any other structure defined on the factors. If one of the factors has a boundary, the product manifold also has a boundary. Cartesian products may be used to construct tori and finite
cylinders, for example, as S
1 × S
1 and S
1 ×
,1 respectively.

History
The study of manifolds combines many important areas of mathematics: it generalizes concepts such as
curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
s and surfaces as well as ideas from
linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrix (mathemat ...
and topology.
Early development
Before the modern concept of a manifold there were several important results.
Non-Euclidean geometry considers spaces where
Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
's
parallel postulate fails.
Saccheri first studied such geometries in 1733, but sought only to disprove them.
Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, Geodesy, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observat ...
,
Bolyai and
Lobachevsky independently discovered them 100 years later. Their research uncovered two types of spaces whose geometric structures differ from that of classical Euclidean space; these gave rise to
hyperbolic geometry and
elliptic geometry. In the modern theory of manifolds, these notions correspond to Riemannian manifolds with constant negative and positive
curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
, respectively.
Carl Friedrich Gauss may have been the first to consider abstract spaces as mathematical objects in their own right. His
theorema egregium gives a method for computing the curvature of a
surface without considering the
ambient space in which the surface lies. Such a surface would, in modern terminology, be called a manifold; and in modern terms, the theorem proved that the curvature of the surface is an
intrinsic property. Manifold theory has come to focus exclusively on these intrinsic properties (or invariants), while largely ignoring the extrinsic properties of the ambient space.
Another, more topological example of an intrinsic
property
Property is a system of rights that gives people legal control of valuable things, and also refers to the valuable things themselves. Depending on the nature of the property, an owner of property may have the right to consume, alter, share, re ...
of a manifold is its
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's ...
.
Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
showed that for a convex
polytope in the three-dimensional Euclidean space with ''V''
vertices (or corners), ''E'' edges, and ''F'' faces,
The same formula will hold if we project the vertices and edges of the polytope onto a sphere, creating a
topological map with ''V'' vertices, ''E'' edges, and ''F'' faces, and in fact, will remain true for any spherical map, even if it does not arise from any convex polytope. Thus 2 is a topological invariant of the sphere, called its Euler characteristic. On the other hand, a
torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
can be sliced open by its 'parallel' and 'meridian' circles, creating a map with ''V'' = 1 vertex, ''E'' = 2 edges, and ''F'' = 1 face. Thus the Euler characteristic of the torus is 1 − 2 + 1 = 0. The Euler characteristic of other surfaces is a useful
topological invariant, which can be extended to higher dimensions using
Betti numbers. In the mid nineteenth century, the
Gauss–Bonnet theorem linked the Euler characteristic to the
Gaussian curvature.
Synthesis
Investigations of
Niels Henrik Abel and
Carl Gustav Jacobi on inversion of
elliptic integral
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising i ...
s in the first half of 19th century led them to consider special types of complex manifolds, now known as
Jacobians.
Bernhard Riemann
Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the f ...
further contributed to their theory, clarifying the geometric meaning of the process of
analytic continuation of functions of complex variables.
Another important source of manifolds in 19th century mathematics was
analytical mechanics, as developed by
Siméon Poisson, Jacobi, and
William Rowan Hamilton. The possible states of a mechanical system are thought to be points of an abstract space,
phase space in
Lagrangian and
Hamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
formalisms of classical mechanics. This space is, in fact, a high-dimensional manifold, whose dimension corresponds to the degrees of freedom of the system and where the points are specified by their
generalized coordinates. For an unconstrained movement of free particles the manifold is equivalent to the Euclidean space, but various
conservation laws constrain it to more complicated formations, e.g.
Liouville tori. The theory of a rotating solid body, developed in the 18th century by Leonhard Euler and
Joseph-Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi Lagrangia[Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...](_blank)
, one of the founders of topology.
Riemann was the first one to do extensive work generalizing the idea of a surface to higher dimensions. The name ''manifold'' comes from Riemann's original
German term, ''Mannigfaltigkeit'', which
William Kingdon Clifford translated as "manifoldness". In his Göttingen inaugural lecture, Riemann described the set of all possible values of a variable with certain constraints as a ''Mannigfaltigkeit'', because the variable can have ''many'' values. He distinguishes between ''stetige Mannigfaltigkeit'' and ''diskrete'' ''Mannigfaltigkeit'' (''continuous manifoldness'' and ''discontinuous manifoldness''), depending on whether the value changes continuously or not. As continuous examples, Riemann refers to not only colors and the locations of objects in space, but also the possible shapes of a spatial figure. Using
induction, Riemann constructs an ''n-fach ausgedehnte Mannigfaltigkeit'' (''n times extended manifoldness'' or ''n-dimensional manifoldness'') as a continuous stack of (n−1) dimensional manifoldnesses. Riemann's intuitive notion of a ''Mannigfaltigkeit'' evolved into what is today formalized as a manifold. Riemannian manifolds and
Riemann surfaces are named after Riemann.
Poincaré's definition
In his very influential paper,
Analysis Situs, Henri Poincaré gave a definition of a differentiable manifold (''variété'') which served as a precursor to the modern concept of a manifold.
In the first section of Analysis Situs, Poincaré defines a manifold as the
level set of a
continuously differentiable function between Euclidean spaces that satisfies the nondegeneracy hypothesis of the
implicit function theorem. In the third section, he begins by remarking that the
graph of a continuously differentiable function is a manifold in the latter sense. He then proposes a new, more general, definition of manifold based on a 'chain of manifolds' (''une chaîne des variétés'').
Poincaré's notion of a ''chain of manifolds'' is a precursor to the modern notion of atlas. In particular, he considers two manifolds defined respectively as graphs of functions
and
. If these manifolds overlap (''a une partie commune''), then he requires that the coordinates
depend continuously differentiably on the coordinates
and vice versa (...les
sont fonctions analytiques des
et inversement''
'). In this way he introduces a precursor to the notion of a
chart
A chart (sometimes known as a graph) is a graphics, graphical representation for data visualization, in which "the data is represented by symbols, such as bars in a bar chart, lines in a line chart, or slices in a pie chart". A chart can repres ...
and of a
transition map
In mathematics, particularly topology, an atlas is a concept used to describe a manifold. An atlas consists of individual ''charts'' that, roughly speaking, describe individual regions of the manifold. In general, the notion of atlas underlies t ...
.
For example, the unit circle in the plane can be thought of as the graph of the function
or else the function
in a neighborhood of every point except the points (1, 0) and (−1, 0); and in a neighborhood of those points, it can be thought of as the graph of, respectively,
and
. The circle can be represented by a graph in the neighborhood of every point because the left hand side of its defining equation
has nonzero gradient at every point of the circle. By the
implicit function theorem, every
submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S \rightarrow M satisfies certain properties. There are different types of submanifolds depending on exactly ...
of Euclidean space is locally the graph of a function.
Hermann Weyl
Hermann Klaus Hugo Weyl (; ; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist, logician and philosopher. Although much of his working life was spent in Zürich, Switzerland, and then Princeton, New Jersey, ...
gave an intrinsic definition for differentiable manifolds in his lecture course on Riemann surfaces in 1911–1912, opening the road to the general concept of a
topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
that followed shortly. During the 1930s
Hassler Whitney and others clarified the
foundational aspects of the subject, and thus intuitions dating back to the latter half of the 19th century became precise, and developed through
differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
and
Lie group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
A manifold is a space that locally resembles Eucli ...
theory. Notably, the
Whitney embedding theorem showed that the intrinsic definition in terms of charts was equivalent to Poincaré's definition in terms of subsets of Euclidean space.
Topology of manifolds: highlights
Two-dimensional manifolds, also known as a 2D ''surfaces'' embedded in our common 3D space, were considered by Riemann under the guise of
Riemann surfaces, and rigorously classified in the beginning of the 20th century by
Poul Heegaard and
Max Dehn
Max Wilhelm Dehn (November 13, 1878 – June 27, 1952) was a German mathematician most famous for his work in geometry, topology and geometric group theory. Dehn's early life and career took place in Germany. However, he was forced to retire in 1 ...
. Poincaré pioneered the study of three-dimensional manifolds and raised a fundamental question about them, today known as the
Poincaré conjecture. After nearly a century,
Grigori Perelman proved the Poincaré conjecture (see the
Solution of the Poincaré conjecture).
William Thurston
William Paul Thurston (October 30, 1946August 21, 2012) was an American mathematician. He was a pioneer in the field of low-dimensional topology and was awarded the Fields Medal in 1982 for his contributions to the study of 3-manifolds.
Thurst ...
's
geometrization program, formulated in the 1970s, provided a far-reaching extension of the Poincaré conjecture to the general three-dimensional manifolds. Four-dimensional manifolds were brought to the forefront of mathematical research in the 1980s by
Michael Freedman and in a different setting, by
Simon Donaldson, who was motivated by the then recent progress in theoretical physics (
Yang–Mills theory), where they serve as a substitute for ordinary 'flat'
spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
.
Andrey Markov Jr. showed in 1960 that no algorithm exists for classifying four-dimensional manifolds. Important work on higher-dimensional manifolds, including
analogues of the Poincaré conjecture, had been done earlier by
René Thom,
John Milnor,
Stephen Smale and
Sergei Novikov. A very pervasive and flexible technique underlying much work on the
topology of manifolds is
Morse theory.
Additional structure
Topological manifolds
The simplest kind of manifold to define is the topological manifold, which looks locally like some "ordinary" Euclidean space
. By definition, all manifolds are topological manifolds, so the phrase "topological manifold" is usually used to emphasize that a manifold lacks additional structure, or that only its topological properties are being considered. Formally, a topological manifold is a topological space
locally homeomorphic to a Euclidean space. This means that every point has a neighbourhood for which there exists a
homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function ...
(a
bijective continuous function whose inverse is also continuous) mapping that neighbourhood to
. These homeomorphisms are the charts of the manifold.
A ''topological'' manifold looks locally like a Euclidean space in a rather weak manner: while for each individual chart it is possible to distinguish differentiable functions or measure distances and angles, merely by virtue of being a topological manifold a space does not have any ''particular'' and ''consistent'' choice of such concepts. In order to discuss such properties for a manifold, one needs to specify further structure and consider
differentiable manifolds and
Riemannian manifolds discussed below. In particular, the same underlying topological manifold can have several mutually incompatible classes of differentiable functions and an infinite number of ways to specify distances and angles.
Usually additional technical assumptions on the topological space are made to exclude pathological cases. It is customary to require that the space be
Hausdorff and
second countable.
The ''dimension'' of the manifold at a certain point is the dimension of the Euclidean space that the charts at that point map to (number ''n'' in the definition). All points in a
connected manifold have the same dimension. Some authors require that all charts of a topological manifold map to Euclidean spaces of same dimension. In that case every topological manifold has a topological invariant, its dimension.
Differentiable manifolds
For most applications, a special kind of topological manifold, namely, a differentiable manifold, is used. If the local charts on a manifold are compatible in a certain sense, one can define directions, tangent spaces, and differentiable functions on that manifold. In particular it is possible to use
calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
on a differentiable manifold. Each point of an ''n''-dimensional differentiable manifold has a
tangent space. This is an ''n''-dimensional Euclidean space consisting of the
tangent vectors of the curves through the point.
Two important classes of differentiable manifolds are smooth and
analytic manifolds. For smooth manifolds the transition maps are smooth, that is, infinitely differentiable. Analytic manifolds are smooth manifolds with the additional condition that the transition maps are
analytic (they can be expressed as
power series). The sphere can be given analytic structure, as can most familiar curves and surfaces.
A
rectifiable set generalizes the idea of a piecewise smooth or
rectifiable curve to higher dimensions; however, rectifiable sets are not in general manifolds.
Riemannian manifolds
To measure distances and angles on manifolds, the manifold must be Riemannian. A ''Riemannian manifold'' is a differentiable manifold in which each
tangent space is equipped with an
inner product
In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, ofte ...
in a manner which varies smoothly from point to point. Given two tangent vectors
and
, the inner product
gives a real number. The
dot (or scalar) product is a typical example of an inner product. This allows one to define various notions such as length,
angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s,
area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-di ...
s (or
volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
s),
curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
and
divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
of
vector fields.
All differentiable manifolds (of constant dimension) can be given the structure of a Riemannian manifold. The Euclidean space itself carries a natural structure of Riemannian manifold (the tangent spaces are naturally identified with the Euclidean space itself and carry the standard scalar product of the space). Many familiar curves and surfaces, including for example all -spheres, are specified as subspaces of a Euclidean space and inherit a metric from their embedding in it.
Finsler manifolds
A Finsler manifold allows the definition of distance but does not require the concept of angle; it is an analytic manifold in which each tangent space is equipped with a
norm,
, in a manner which varies smoothly from point to point. This norm can be extended to a
metric, defining the length of a curve; but it cannot in general be used to define an inner product.
Any Riemannian manifold is a Finsler manifold.
Lie groups
Lie groups, named after
Sophus Lie
Marius Sophus Lie ( ; ; 17 December 1842 – 18 February 1899) was a Norwegian mathematician. He largely created the theory of continuous symmetry and applied it to the study of geometry and differential equations. He also made substantial cont ...
, are differentiable manifolds that carry also the structure of a
group which is such that the group operations are defined by smooth maps.
A Euclidean vector space with the group operation of vector addition is an example of a non-compact Lie group. A simple example of a
compact Lie group is the circle: the group operation is simply rotation. This group, known as
, can be also characterised as the group of
complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s of
modulus 1 with multiplication as the group operation.
Other examples of Lie groups include special groups of
matrices, which are all subgroups of the
general linear group
In mathematics, the general linear group of degree n is the set of n\times n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again inve ...
, the group of
matrices with non-zero determinant. If the matrix entries are
real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s, this will be an
-dimensional disconnected manifold. The
orthogonal group
In mathematics, the orthogonal group in dimension , denoted , is the Group (mathematics), group of isometry, distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by ...
s, the
symmetry groups of the sphere and
hyperspheres, are
dimensional manifolds, where
is the dimension of the sphere. Further examples can be found in the
table of Lie groups.
Other types of manifolds
* A ''
complex manifold
In differential geometry and complex geometry, a complex manifold is a manifold with a ''complex structure'', that is an atlas (topology), atlas of chart (topology), charts to the open unit disc in the complex coordinate space \mathbb^n, such th ...
'' is a manifold whose charts take values in
and whose transition functions are
holomorphic on the overlaps. These manifolds are the basic objects of study in
complex geometry. A one-complex-dimensional manifold is called a
Riemann surface. An
-dimensional complex manifold has dimension
as a real differentiable manifold.
* A ''
CR manifold'' is a manifold modeled on boundaries of domains in
.
* 'Infinite dimensional manifolds': to allow for infinite dimensions, one may consider
Banach manifolds which are locally homeomorphic to
Banach space
In mathematics, more specifically in functional analysis, a Banach space (, ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and ...
s. Similarly, Fréchet manifolds are locally homeomorphic to
Fréchet spaces.
* A ''
symplectic manifold'' is a kind of manifold which is used to represent the phase spaces in
classical mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics inv ...
. They are endowed with a
2-form that defines the
Poisson bracket. A closely related type of manifold is a
contact manifold.
* A ''
combinatorial manifold'' is a kind of manifold which is discretization of a manifold. It usually means a
piecewise linear manifold made by
simplicial complexes.
* A ''
digital manifold'' is a special kind of combinatorial manifold which is defined in digital space. See
digital topology.
Classification and invariants
Different notions of manifolds have different notions of classification and invariant; in this section we focus on smooth closed manifolds.
The classification of smooth closed manifolds is well understood ''in principle'', except in
dimension 4: in low dimensions (2 and 3) it is geometric, via the
uniformization theorem
In mathematics, the uniformization theorem states that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generali ...
and the
solution of the Poincaré conjecture, and in high dimension (5 and above) it is algebraic, via
surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one finite-dimensional manifold from another in a 'controlled' way, introduced by . Milnor called this technique ''surgery'', while An ...
. This is a classification in principle: the general question of whether two smooth manifolds are diffeomorphic is not computable in general. Further, specific computations remain difficult, and there are many open questions.
Orientable surfaces can be visualized, and their diffeomorphism classes enumerated, by genus. Given two orientable surfaces, one can determine if they are diffeomorphic by computing their respective genera and comparing: they are diffeomorphic if and only if the genera are equal, so the genus forms a
complete set of invariants In mathematics, a complete set of invariants for a classification problem is a collection of maps
:f_i : X \to Y_i
(where X is the collection of objects being classified, up to some equivalence relation \sim, and the Y_i are some sets), such that ...
.
This is much harder in higher dimensions: higher-dimensional manifolds cannot be directly visualized (though visual intuition is useful in understanding them), nor can their diffeomorphism classes be enumerated, nor can one in general determine if two different descriptions of a higher-dimensional manifold refer to the same object.
However, one can determine if two manifolds are ''different'' if there is some intrinsic characteristic that differentiates them. Such criteria are commonly referred to as
invariants, because, while they may be defined in terms of some presentation (such as the genus in terms of a triangulation), they are the same relative to all possible descriptions of a particular manifold: they are ''invariant'' under different descriptions.
One could hope to develop an arsenal of invariant criteria that would definitively classify all manifolds up to isomorphism. It is known that for manifolds of dimension 4 and higher,
no program exists that can decide whether two manifolds are diffeomorphic.
Smooth manifolds have
a rich set of invariants, coming from
point-set topology, classic algebraic topology, and
geometric topology
In mathematics, geometric topology is the study of manifolds and Map (mathematics)#Maps as functions, maps between them, particularly embeddings of one manifold into another.
History
Geometric topology as an area distinct from algebraic topo ...
. The most familiar invariants, which are visible for surfaces, are
orientability (a normal invariant, also detected by
homology) and
genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
(a homological invariant).
Smooth closed manifolds have no local invariants (other than dimension), though geometric manifolds have local invariants, notably the
curvature of a Riemannian manifold and the
torsion of a manifold equipped with an
affine connection. This distinction between local invariants and no local invariants is a common way to distinguish between geometry and topology. All invariants of a smooth closed manifold are thus global.
Algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
is a source of a number of important global invariant properties. Some key criteria include the ''
simply connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every Path (topology), path between two points can be continuously transformed into any other such path while preserving ...
'' property and orientability (see below). Indeed, several branches of mathematics, such as
homology and
homotopy
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. ...
theory, and the theory of
characteristic classes were founded in order to study invariant properties of manifolds.
Surfaces
Orientability
In dimensions two and higher, a simple but important invariant criterion is the question of whether a manifold admits a meaningful orientation. Consider a topological manifold with charts mapping to
. Given an
ordered basis for
, a chart causes its piece of the manifold to itself acquire a sense of ordering, which in 3-dimensions can be viewed as either right-handed or left-handed. Overlapping charts are not required to agree in their sense of ordering, which gives manifolds an important freedom. For some manifolds, like the sphere, charts can be chosen so that overlapping regions agree on their "handedness"; these are ''
orientable'' manifolds. For others, this is impossible. The latter possibility is easy to overlook, because any closed surface embedded (without self-intersection) in three-dimensional space is orientable.
Some illustrative examples of non-orientable manifolds include: (1) the
Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a Surface (topology), surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Bened ...
, which is a manifold with boundary, (2) the
Klein bottle
In mathematics, the Klein bottle () is an example of a Orientability, non-orientable Surface (topology), surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the ...
, which must intersect itself in its 3-space representation, and (3) the
real projective plane, which arises naturally in geometry.
Möbius strip

Begin with an infinite circular cylinder standing vertically, a manifold without boundary. Slice across it high and low to produce two circular boundaries, and the cylindrical strip between them. This is an orientable manifold with boundary, upon which "surgery" will be performed. Slice the strip open, so that it could unroll to become a rectangle, but keep a grasp on the cut ends. Twist one end 180°, making the inner surface face out, and glue the ends back together seamlessly. This results in a strip with a permanent half-twist: the Möbius strip. Its boundary is no longer a pair of circles, but (topologically) a single circle; and what was once its "inside" has merged with its "outside", so that it now has only a ''single'' side. Similarly to the Klein Bottle below, this two dimensional surface would need to intersect itself in two dimensions, but can easily be constructed in three or more dimensions.
Klein bottle
Take two Möbius strips; each has a single loop as a boundary. Straighten out those loops into circles, and let the strips distort into
cross-caps. Gluing the circles together will produce a new, closed manifold without boundary, the Klein bottle. Closing the surface does nothing to improve the lack of orientability, it merely removes the boundary. Thus, the Klein bottle is a closed surface with no distinction between inside and outside. In three-dimensional space, a Klein bottle's surface must pass through itself. Building a Klein bottle which is not self-intersecting requires four or more dimensions of space.
Real projective plane
Begin with a sphere centered on the origin. Every line through the origin pierces the sphere in two opposite points called ''antipodes''. Although there is no way to do so physically, it is possible (by considering a
quotient space) to mathematically merge each antipode pair into a single point. The closed surface so produced is the real projective plane, yet another non-orientable surface. It has a number of equivalent descriptions and constructions, but this route explains its name: all the points on any given line through the origin project to the same "point" on this "plane".
Genus and the Euler characteristic
For two dimensional manifolds a key invariant property is the
genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
, or "number of handles" present in a surface. A torus is a sphere with one handle, a double torus is a sphere with two handles, and so on. Indeed, it is possible to fully characterize compact, two-dimensional manifolds on the basis of genus and orientability. In higher-dimensional manifolds genus is replaced by the notion of
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's ...
, and more generally
Betti numbers and
homology and
cohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed ...
.
Maps of manifolds
Just as there are various types of manifolds, there are various types of
maps of manifolds. In addition to continuous functions and smooth functions generally, there are maps with special properties. In
geometric topology
In mathematics, geometric topology is the study of manifolds and Map (mathematics)#Maps as functions, maps between them, particularly embeddings of one manifold into another.
History
Geometric topology as an area distinct from algebraic topo ...
a basic type are
embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group (mathematics), group that is a subgroup.
When some object X is said to be embedded in another object Y ...
s, of which
knot theory
In topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be und ...
is a central example, and generalizations such as
immersions,
submersions,
covering space
In topology, a covering or covering projection is a continuous function, map between topological spaces that, intuitively, Local property, locally acts like a Projection (mathematics), projection of multiple copies of a space onto itself. In par ...
s, and
ramified covering spaces.
Basic results include the
Whitney embedding theorem and
Whitney immersion theorem.
In Riemannian geometry, one may ask for maps to preserve the Riemannian metric, leading to notions of
isometric embeddings,
isometric immersions, and
Riemannian submersions; a basic result is the
Nash embedding theorem.
Scalar-valued functions
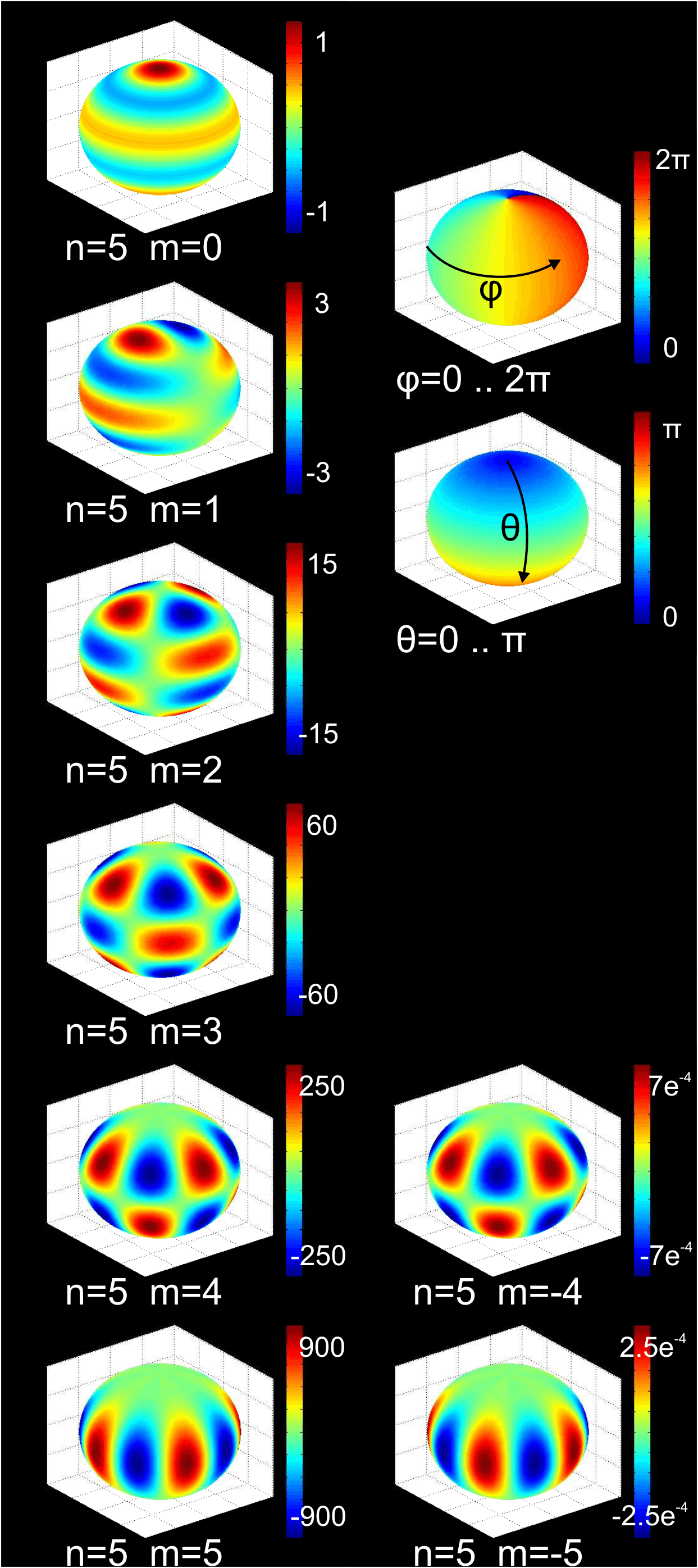
A basic example of maps between manifolds are scalar-valued functions on a manifold,
or
sometimes called
regular functions or
functionals, by analogy with algebraic geometry or linear algebra. These are of interest both in their own right, and to study the underlying manifold.
In geometric topology, most commonly studied are
Morse function
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differenti ...
s, which yield
handlebody decompositions, while in
mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series ( ...
, one often studies solution to
partial differential equations, an important example of which is
harmonic analysis, where one studies
harmonic functions: the kernel of the
Laplace operator
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a Scalar field, scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \ ...
. This leads to such functions as the
spherical harmonics, and to
heat kernel methods of studying manifolds, such as
hearing the shape of a drum and some proofs of the
Atiyah–Singer index theorem.
Generalizations of manifolds
;Infinite dimensional manifolds: The definition of a manifold can be generalized by dropping the requirement of finite dimensionality. Thus an infinite dimensional manifold is a topological space locally homeomorphic to a
topological vector space
In mathematics, a topological vector space (also called a linear topological space and commonly abbreviated TVS or t.v.s.) is one of the basic structures investigated in functional analysis.
A topological vector space is a vector space that is als ...
over the reals. This omits the point-set axioms, allowing higher cardinalities and
non-Hausdorff manifolds; and it omits finite dimension, allowing structures such as
Hilbert manifolds to be modeled on
Hilbert spaces,
Banach manifolds to be modeled on
Banach space
In mathematics, more specifically in functional analysis, a Banach space (, ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and ...
s, and
Fréchet manifolds to be modeled on
Fréchet spaces. Usually one relaxes one or the other condition: manifolds with the point-set axioms are studied in
general topology, while infinite-dimensional manifolds are studied in
functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, Inner product space#Definition, inner product, Norm (mathematics ...
.
;Orbifolds: An
orbifold is a generalization of manifold allowing for certain kinds of "
singularities" in the topology. Roughly speaking, it is a space which locally looks like the quotients of some simple space (''e.g.'' Euclidean space) by the
actions of various
finite group
In abstract algebra, a finite group is a group whose underlying set is finite. Finite groups often arise when considering symmetry of mathematical or physical objects, when those objects admit just a finite number of structure-preserving tra ...
s. The singularities correspond to fixed points of the group actions, and the actions must be compatible in a certain sense.
;Algebraic varieties and schemes:
Non-singular algebraic varieties over the real or complex numbers are manifolds. One generalizes this first by allowing singularities, secondly by allowing different fields, and thirdly by emulating the patching construction of manifolds: just as a manifold is glued together from open subsets of Euclidean space, an
algebraic variety
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the solution set, set of solutions of a system of polynomial equations over the real number, ...
is glued together from affine algebraic varieties, which are zero sets of polynomials over algebraically closed fields.
Schemes are likewise glued together from affine schemes, which are a generalization of algebraic varieties. Both are related to manifolds, but are constructed algebraically using
sheaves instead of atlases.
:Because of
singular points, a variety is in general not a manifold, though linguistically the French ''variété'', German ''Mannigfaltigkeit'' and English ''manifold'' are largely
synonymous. In French an algebraic variety is called ''une
variété algébrique'' (an ''algebraic variety''), while a smooth manifold is called ''une
variété différentielle'' (a ''differential variety'').
;Stratified space: A "stratified space" is a space that can be divided into pieces ("strata"), with each stratum a manifold, with the strata fitting together in prescribed ways (formally, a
filtration by closed subsets).
There are various technical definitions, notably a Whitney stratified space (see
Whitney conditions) for smooth manifolds and a
topologically stratified space for topological manifolds. Basic examples include
manifold with boundary (top dimensional manifold and codimension 1 boundary) and manifolds with corners (top dimensional manifold, codimension 1 boundary, codimension 2 corners). Whitney stratified spaces are a broad class of spaces, including algebraic varieties, analytic varieties,
semialgebraic sets, and
subanalytic sets.
;CW-complexes: A
CW complex
In mathematics, and specifically in topology, a CW complex (also cellular complex or cell complex) is a topological space that is built by gluing together topological balls (so-called ''cells'') of different dimensions in specific ways. It generali ...
is a topological space formed by gluing disks of different dimensionality together. In general the resulting space is singular, hence not a manifold. However, they are of central interest in algebraic topology, especially in
homotopy theory.
;Homology manifolds: A
homology manifold is a space that behaves like a manifold from the point of view of homology theory. These are not all manifolds, but (in high dimension) can be analyzed by surgery theory similarly to manifolds, and failure to be a manifold is a local obstruction, as in surgery theory.
;Differential spaces: Let
be a nonempty set. Suppose that some family of real functions on
was chosen. Denote it by
. It is an algebra with respect to the pointwise addition and multiplication. Let
be equipped with the topology induced by
. Suppose also that the following conditions hold. First: for every
, where
, and arbitrary
, the composition
. Second: every function, which in every point of
locally coincides with some function from
, also belongs to
. A pair
for which the above conditions hold, is called a Sikorski differential space.
See also
*
*
* : statistics on manifolds
*
*
*
By dimension
*
*
*
*
Notes
References
*
Freedman, Michael H., and Quinn, Frank (1990) ''Topology of 4-Manifolds''. Princeton University Press. .
*
Guillemin, Victor and Pollack, Alan (1974) ''Differential Topology''. Prentice-Hall. . Advanced undergraduate / first-year graduate text inspired by Milnor.
* Hempel, John (1976) ''3-Manifolds''. Princeton University Press. .
*
Hirsch, Morris, (1997) ''Differential Topology''. Springer Verlag. . The most complete account, with historical insights and excellent, but difficult, problems. The standard reference for those wishing to have a deep understanding of the subject.
*
Kirby, Robion C. and Siebenmann, Laurence C. (1977) ''Foundational Essays on Topological Manifolds. Smoothings, and Triangulations''. Princeton University Press. . A detailed study of the
category of topological manifolds.
* Lee, John M. (2000) ''Introduction to Topological Manifolds''. Springer-Verlag. . Detailed and comprehensive first-year graduate text.
* Lee, John M. (2003)
Introduction to Smooth Manifolds'. Springer-Verlag. . Detailed and comprehensive first-year graduate text; sequel to ''Introduction to Topological Manifolds''.
*
Massey, William S. (1977) ''Algebraic Topology: An Introduction''. Springer-Verlag. .
*
Milnor, John (1997) ''Topology from the Differentiable Viewpoint''. Princeton University Press. . Classic brief introduction to differential topology.
*
Munkres, James R. (1991)
Analysis on Manifolds'. Addison-Wesley (reprinted by Westview Press) . Undergraduate text treating manifolds in
.
*
Munkres, James R. (2000) ''Topology''. Prentice Hall. .
* Neuwirth, L. P., ed. (1975) ''Knots, Groups, and 3-Manifolds. Papers Dedicated to the Memory of R. H. Fox''. Princeton University Press. .
*
Riemann, Bernhard, ''Gesammelte mathematische Werke und wissenschaftlicher Nachlass'', Sändig Reprint. .
**
Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse.' The 1851 doctoral thesis in which "manifold" (''Mannigfaltigkeit'') first appears.
**
Ueber die Hypothesen, welche der Geometrie zu Grunde liegen.' The 1854 Göttingen inaugural lecture (''Habilitationsschrift'').
*
Spivak, Michael (1965)
Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus'. W.A. Benjamin Inc. (reprinted by Addison-Wesley and Westview Press). .
Famously terse advanced undergraduate / first-year graduate text.
*
Spivak, Michael (1999) ''A Comprehensive Introduction to Differential Geometry'' (3rd edition) Publish or Perish Inc. Encyclopedic five-volume series presenting a systematic treatment of the theory of manifolds, Riemannian geometry, classical differential geometry, and numerous other topics at the first- and second-year graduate levels.
* . Concise first-year graduate text.
External links
*
Dimensions-math.org(A film explaining and visualizing manifolds up to fourth dimension.)
* Th
manifold atlasproject of th
Max Planck Institute for Mathematics in Bonn* MIT Open Courseware
Geometry of Manifolds
{{Authority control
Geometry processing
 In
In  A manifold with boundary is a manifold with an edge. For example, a disk (circle plus interior) is a 2-manifold with as boundary the circle, a 1-manifold. The boundary of an -manifold with boundary is an -manifold. In three dimensions, a ball (sphere plus interior) is a 3-manifold with boundary. Its boundary is a sphere, a 2-manifold.
In technical language, a manifold with boundary is a space containing both interior points and boundary points. Every interior point has a neighborhood homeomorphic to the open -ball . Every boundary point has a neighborhood homeomorphic to the "half" -ball . Any homeomorphism between half-balls must send points with to points with . This invariance allows to "define" boundary points; see next paragraph.
If in addition we are considering differentiable manifolds, then a
A manifold with boundary is a manifold with an edge. For example, a disk (circle plus interior) is a 2-manifold with as boundary the circle, a 1-manifold. The boundary of an -manifold with boundary is an -manifold. In three dimensions, a ball (sphere plus interior) is a 3-manifold with boundary. Its boundary is a sphere, a 2-manifold.
In technical language, a manifold with boundary is a space containing both interior points and boundary points. Every interior point has a neighborhood homeomorphic to the open -ball . Every boundary point has a neighborhood homeomorphic to the "half" -ball . Any homeomorphism between half-balls must send points with to points with . This invariance allows to "define" boundary points; see next paragraph.
If in addition we are considering differentiable manifolds, then a  A basic example of maps between manifolds are scalar-valued functions on a manifold,
or
sometimes called regular functions or functionals, by analogy with algebraic geometry or linear algebra. These are of interest both in their own right, and to study the underlying manifold.
In geometric topology, most commonly studied are
A basic example of maps between manifolds are scalar-valued functions on a manifold,
or
sometimes called regular functions or functionals, by analogy with algebraic geometry or linear algebra. These are of interest both in their own right, and to study the underlying manifold.
In geometric topology, most commonly studied are