|
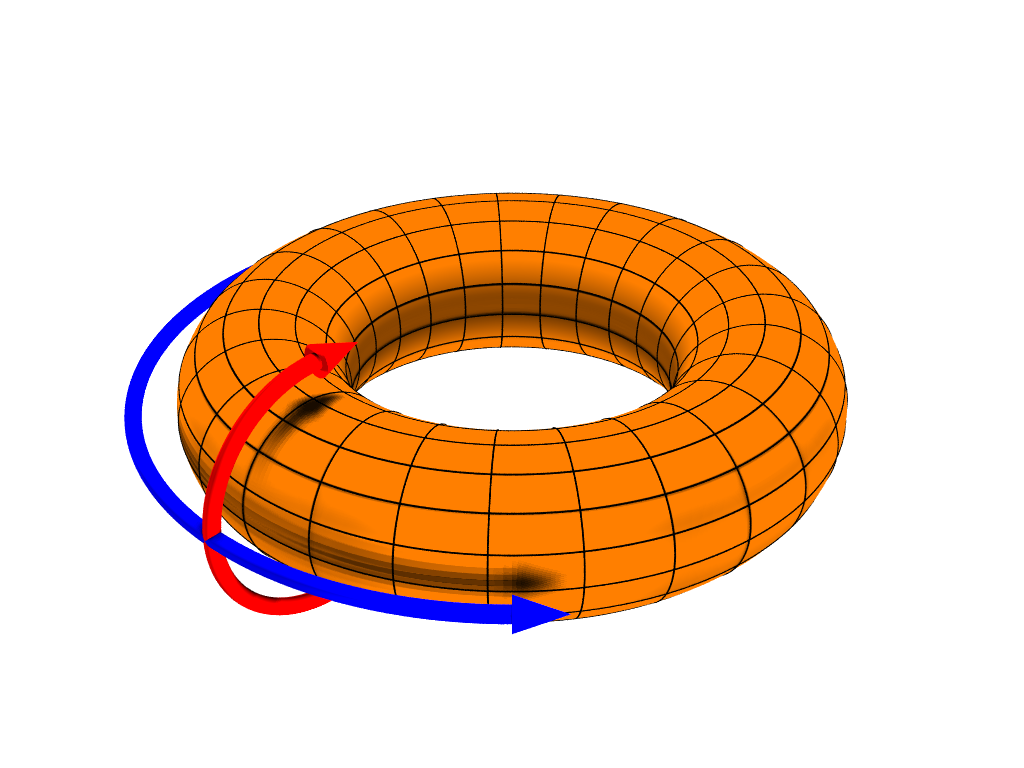
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Torus Cycles
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a '' toroid'', as in a square toroid. Real-world objects that ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Clifford Torus
In geometric topology, the Clifford torus is the simplest and most symmetric flat embedding of the Cartesian product of two circles and (in the same sense that the surface of a cylinder is "flat"). It is named after William Kingdon Clifford. The Clifford torus is embedded in , as opposed to in . This is necessary since and each exists in their own independent embedding space and , the resulting product space will be rather than . The historically popular view that the Cartesian product of two circles is an torus in contrast requires the highly asymmetric application of a rotation operator to the second circle, since that circle will only have one independent axis available to it after the first circle consumes and . Stated another way, a torus embedded in is an asymmetric reduced-dimension projection of the maximally symmetric Clifford torus embedded in . The relationship is similar to that of projecting the edges of a cube onto a sheet of paper. Such a proj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Torsion (mechanics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a Set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of List of continuity-related mathematical topics, continuity. Euclidean spaces, and, more generally, metric spaces are examples of topological spaces, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and Homotopy, homotopies. A property that is invariant under such deformations is a to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Genus (mathematics)
In mathematics, genus (: genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic \chi, via the relationship \chi=2-2g for closed surfaces, where g is the genus. For surfaces with b boundary components, the equation reads \chi=2-2g-b. In layman's terms, the genus is the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 such hole, while a sphere has 0. The green surface pictured above has 2 holes of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Doughnut
A doughnut or donut () is a type of pastry made from leavened fried dough. It is popular in many countries and is prepared in various forms as a sweet snack that can be homemade or purchased in bakeries, supermarkets, food stalls, and franchised specialty vendors. ''Doughnut'' is the traditional spelling, while ''donut'' is the simplified version; the terms are used interchangeably. Doughnuts are usually deep fried from a flour dough, but other types of batters can also be used. Various toppings and flavors are used for different types, such as sugar, chocolate or maple glazing. Doughnuts may also include water, leavening, eggs, milk, sugar, oil, shortening, and natural or artificial flavors. The two most common types are the ring doughnut and the filled doughnut, which is injected with fruit preserves (the jelly doughnut), cream, custard, or other sweet fillings. Small pieces of dough are sometimes cooked as doughnut holes. Once fried, doughnuts may be glazed with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Klein Bottle
In mathematics, the Klein bottle () is an example of a Orientability, non-orientable Surface (topology), surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is a two-dimensional manifold on which one cannot define a normal vector at each point that varies continuous function, continuously over the whole manifold. Other related non-orientable surfaces include the Möbius strip and the real projective plane. While a Möbius strip is a surface with a Boundary (topology), boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary. The Klein bottle was first described in 1882 by the mathematician Felix Klein. Construction The following square is a fundamental polygon of the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Toroid
In mathematics, a toroid is a surface of revolution with a hole in the middle. The axis of revolution passes through the hole and so does not intersect the surface. For example, when a rectangle is rotated around an axis parallel to one of its edges, then a hollow rectangle-section ring is produced. If the revolved figure is a circle, then the object is called a torus. The term ''toroid'' is also used to describe a toroidal polyhedron. In this context a toroid need not be circular and may have any number of holes. A ''g''-holed ''toroid'' can be seen as approximating the surface of a torus having a topological genus, ''g'', of 1 or greater. The Euler characteristic χ of a ''g'' holed toroid is 2(1−''g''). The torus is an example of a toroid, which is the surface of a doughnut. Doughnuts are an example of a solid torus created by rotating a disk, and are not toroids. Toroidal structures occur in both natural and synthetic materials. Equations A toroid is specified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. Very roughly speaking, a topological space is a geometric object, and a homeomorphism results from a continuous deformation of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this description can be misleading. Some continuous deformations do not produce homeomorphisms, such as the deformation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ring Torus To Degenerate Torus (Short)
(The) Ring(s) may refer to: * Ring (jewellery), a round band, usually made of metal, worn as ornamental jewelry * To make a sound with a bell, and the sound made by a bell Arts, entertainment, and media Film and TV * ''The Ring'' (franchise), a Japanese horror media franchise based on the novel series by Koji Suzuki ** ''Ring'' (film), or ''The Ring'', a 1998 Japanese horror film by Hideo Nakata *** ''The Ring'' (2002 film), an American horror film, remake of the 1998 Japanese film ** ''Ring'' (1995 film), a TV film ** ''Rings'' (2005 film), a short film by Jonathan Liebesman ** ''Rings'' (2017 film), an American horror film * "Ring", a season 3 episode of ''Servant'' (TV series) Gaming * ''Ring'' (video game), 1998 * Rings (''Sonic the Hedgehog''), a collectible in ''Sonic the Hedgehog'' games Literature * ''Ring'' (Baxter novel), a 1994 science fiction novel * ''Ring'' (Alexis novel), a 2021 Canadian novel by André Alexis * ''Ring'' (novel series), a Japanese nov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Solid Torus
In mathematics, a solid torus is the topological space formed by sweeping a disk around a circle. It is homeomorphic to the Cartesian product S^1 \times D^2 of the disk and the circle, endowed with the product topology. A standard way to visualize a solid torus is as a toroid, embedded in 3-space. However, it should be distinguished from a torus, which has the same visual appearance: the torus is the two-dimensional space on the boundary of a toroid, while the solid torus includes also the compact interior space enclosed by the torus. A solid torus is a torus plus the volume inside the torus. Real-world objects that approximate a ''solid torus'' include O-rings, non-inflatable lifebuoys, ring doughnuts, and bagels. Topological properties The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary. The boundary is homeomorphic to S^1 \times S^1, the ordinary torus. Since the disk D^2 is contractible, the solid torus has the homotopy type o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lemon (geometry)
In geometry, a lemon is a geometric shape that is constructed as the surface of revolution of a circular arc of angle less than half of a full circle rotated about an axis passing through the endpoints of the lens (or arc). The surface of revolution of the complementary arc of the same circle, through the same axis, is called an apple. The apple and lemon together make up a spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). The lemon forms the boundary of a convex set, while its surrounding apple is non-convex. The ball in North American football has a shape resembling a geometric lemon. However, although used with a related meaning in geometry, the term "football" is more commonly used to refer to a surface of revolution whose Gaussian curvature is positive and constant, formed from a more complicated curve than a circular arc. Alternatively, a football may refer to a more abstract orbifold, a surface modeled locally on a sphere except at two points. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bagel
A bagel (; ; also spelled beigel) is a bread roll originating in the Jewish communities of Poland. Bagels are traditionally made from yeasted wheat dough that is shaped by hand into a torus or ring, briefly boiled in water, and then baked. The result is a dense, chewy, doughy interior with a browned and sometimes crisp exterior. Bagels are often topped with seeds baked on the outer crust—traditional choices include poppy and sesame seeds—or with salt grains. Different dough types include whole-grain and rye. The basic roll-with-a-hole design, hundreds of years old, allows even cooking and baking of the dough; it also allows groups of bagels to be gathered on a string or dowel for handling, transportation, and retail display. The earliest known mention of a boiled-then-baked ring-shaped bread can be found in a 13th-century Syrian cookbook, where they are referred to as . Bagel-like bread known as obwarzanek was common earlier in Poland as seen in royal family account ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |