|
Lemniscate
In algebraic geometry, a lemniscate is any of several figure-eight or -shaped curves. The word comes from the Latin "''lēmniscātus''" meaning "decorated with ribbons", from the Greek λημνίσκος meaning "ribbons",. or which alternatively may refer to the wool from which the ribbons were made. Curves that have been called a lemniscate include three quartic plane curves: the hippopede or lemniscate of Booth, the lemniscate of Bernoulli, and the lemniscate of Gerono. The study of lemniscates (and in particular the hippopede) dates to ancient Greek mathematics, but the term "lemniscate" for curves of this type comes from the work of Jacob Bernoulli in the late 17th century. History and examples Lemniscate of Booth The consideration of curves with a figure-eight shape can be traced back to Proclus, a Greek Neoplatonist philosopher and mathematician who lived in the 5th century AD. Proclus considered the cross-sections of a torus by a plane parallel to the axis of the tor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Of Bernoulli
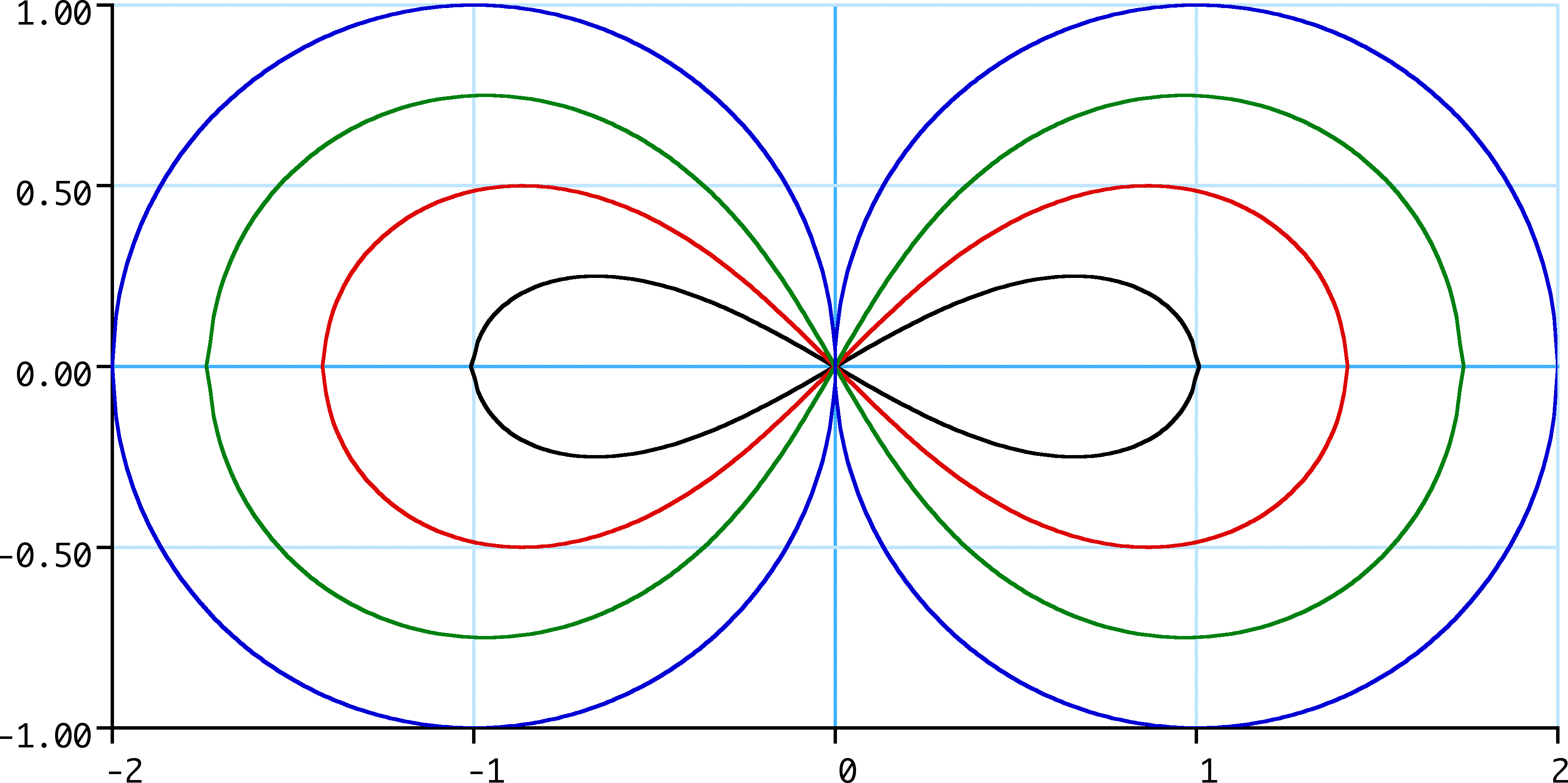
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points and , known as foci, at distance from each other as the locus of points so that . The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from , which is Latin for "decorated with hanging ribbons". It is a special case of the Cassini oval and is a rational algebraic curve of degree 4. This lemniscate was first described in 1694 by Jakob Bernoulli as a modification of an ellipse, which is the locus of points for which the sum of the distances to each of two fixed ''focal points'' is a constant. A Cassini oval, by contrast, is the locus of points for which the ''product'' of these distances is constant. In the case where the curve passes through the point midway between the foci, the oval is a lemniscate of Bernoulli. This curve can be obtained as the inverse transform of a hyperbola, with the inversion circle centered at the center of the hyperbola (bisector o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points and , known as foci, at distance from each other as the locus of points so that . The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from , which is Latin for "decorated with hanging ribbons". It is a special case of the Cassini oval and is a rational algebraic curve of degree 4. This lemniscate was first described in 1694 by Jakob Bernoulli as a modification of an ellipse, which is the locus of points for which the sum of the distances to each of two fixed ''focal points'' is a constant. A Cassini oval, by contrast, is the locus of points for which the ''product'' of these distances is constant. In the case where the curve passes through the point midway between the foci, the oval is a lemniscate of Bernoulli. This curve can be obtained as the inverse transform of a hyperbola, with the inversion circle centered at the center of the hyperbola (bisector o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartic Plane Curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation: :Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0, with at least one of not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space It also follows, from Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 degrees of freedom. A quartic curve can have a maximum of: * Four connected components * Twenty-eight bi-tangents * Three ordinary double points. One may also consider quartic curves over othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Of Gerono
In algebraic geometry, the lemniscate of Gerono, or lemniscate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero and is a lemniscate curve shaped like an \infty symbol, or figure eight. It has equation :x^4-x^2+y^2 = 0. It was studied by Camille-Christophe Gerono. Parameterization Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is :x = \frac,\ y = \frac. Another representation is :x = \cos \varphi,\ y = \sin\varphi\,\cos\varphi = \sin(2\varphi)/2 which reveals that this lemniscate is a special case of a Lissajous figure. Dual curve The dual curve (see Plücker formula In mathematics, a Plücker formula, named after Julius Plücker, is one of a family of formulae, of a type first developed by Plücker in the 1830s, that relate certain numeric invariants of algebraic curves to corresponding invariants of their du ...), pictured below, has therefore a somewhat different character ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacob Bernoulli
Jacob Bernoulli (also known as James or Jacques; – 16 August 1705) was one of the many prominent mathematicians in the Bernoulli family. He was an early proponent of Leibnizian calculus and sided with Gottfried Wilhelm Leibniz during the Leibniz–Newton calculus controversy. He is known for his numerous contributions to calculus, and along with his brother Johann, was one of the founders of the calculus of variations. He also discovered the fundamental mathematical constant . However, his most important contribution was in the field of probability, where he derived the first version of the law of large numbers in his work '' Ars Conjectandi''.Jacob (Jacques) Bernoulli [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cassini Oval
In geometry, a Cassini oval is a quartic plane curve defined as the locus (mathematics), locus of points in the plane (geometry), plane such that the Product_(mathematics), product of the distances to two fixed points (Focus (geometry), foci) is constant. This may be contrasted with an ellipse, for which the ''sum'' of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree of a polynomial, degree 2. Cassini ovals are named after the astronomer Giovanni Domenico Cassini who studied them in the late 17th century. Cassini believed that the Sun traveled around the Earth on one of these ovals, with the Earth at one focus of the oval. Other names include Cassinian ovals, Cassinian curves and ovals of Cassini. Formal definition A Cassini oval is a set of points, such that for any point P of the set, the ''product'' of the distances , PP_1, ,\, , PP_2, to two fixed points P_1, P_2 is a consta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Booth (mathematician)
The Revd Dr James Booth, (1806–1878) was an Anglo-Irish clergyman, notable as a mathematician and educationalist. Life Born at Lavagh, County Leitrim on 26 August 1806, the son of John Booth (cousin to the Gore-Booth baronets), he entered Trinity College, Dublin in 1825 and was elected scholar in 1829, graduating B.A. in 1832, M.A. in 1840, and LL.D. in 1842. Booth left Ireland in 1840 to become Principal of Bristol College, where he had Francis William Newman and William Benjamin Carpenter as colleagues. It had been set up by the British Institution in 1830, to provide non-denominational education. It closed in 1841, however, having suffered some opposition from James Henry Monk. Booth then set up a short-lived private school, where Edward Fry was a pupil. In 1843 he was appointed vice-principal of the Liverpool Collegiate Institution; he had been ordained at Bristol in 1842, and acted there as curate till he moved. In 1848 he gave up his Liverpool post, and moved to London ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. More generally, an algebraic curve is an algebraic variety of dimension one. Equivalently, an algebraic curve is an algebraic variety that is birationally equivalent to an algebraic plane curve. If the curve is contained in an affine space or a projective space, one can take a projection for such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartic Polynomial
In algebra, a quartic function is a function (mathematics), function of the form :f(x)=ax^4+bx^3+cx^2+dx+e, where ''a'' is nonzero, which is defined by a polynomial of Degree of a polynomial, degree four, called a quartic polynomial. A ''quartic equation'', or equation of the fourth degree, is an equation that equates a quartic polynomial to zero, of the form :ax^4+bx^3+cx^2+dx+e=0 , where . The derivative of a quartic function is a cubic function. Sometimes the term biquadratic is used instead of ''quartic'', but, usually, biquadratic function refers to a quadratic function of a square (or, equivalently, to the function defined by a quartic polynomial without terms of odd degree), having the form :f(x)=ax^4+cx^2+e. Since a quartic function is defined by a polynomial of even degree, it has the same infinite limit when the argument goes to positive or negative infinity. If ''a'' is positive, then the function increases to positive infinity at both ends; and thus the function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oval Of Booth
In geometry, a hippopede () is a plane curve determined by an equation of the form :(x^2+y^2)^2=cx^2+dy^2, where it is assumed that and since the remaining cases either reduce to a single point or can be put into the given form with a rotation. Hippopedes are bicircular, rational, algebraic curves of degree 4 and symmetric with respect to both the and axes. Special cases When ''d'' > 0 the curve has an oval form and is often known as an oval of Booth, and when the curve resembles a sideways figure eight, or lemniscate, and is often known as a lemniscate of Booth, after 19th-century mathematician James Booth who studied them. Hippopedes were also investigated by Proclus (for whom they are sometimes called Hippopedes of Proclus) and Eudoxus. For , the hippopede corresponds to the lemniscate of Bernoulli. Definition as spiric sections Hippopedes can be defined as the curve formed by the intersection of a torus and a plane, where the plane is parallel to the axis of the to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point. Similarly, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |