Killing vector fields on:
[Wikipedia]
[Google]
[Amazon]
In
 The vector field on a circle that points clockwise and has the same length at each point is a Killing vector field, since moving each point on the circle along this vector field simply rotates the circle.
The vector field on a circle that points clockwise and has the same length at each point is a Killing vector field, since moving each point on the circle along this vector field simply rotates the circle.
 A toy example for a Killing vector field is on the
A toy example for a Killing vector field is on the
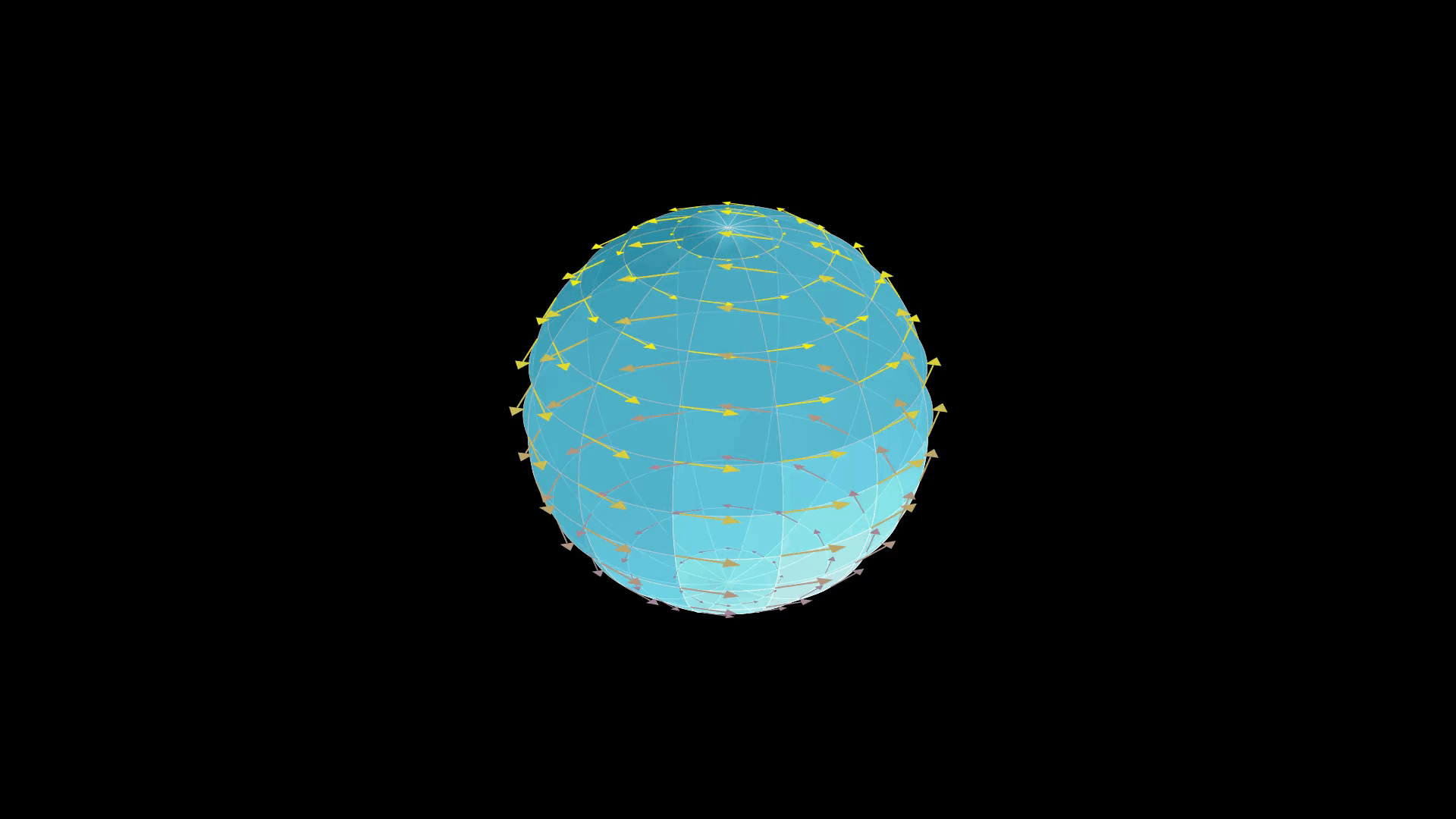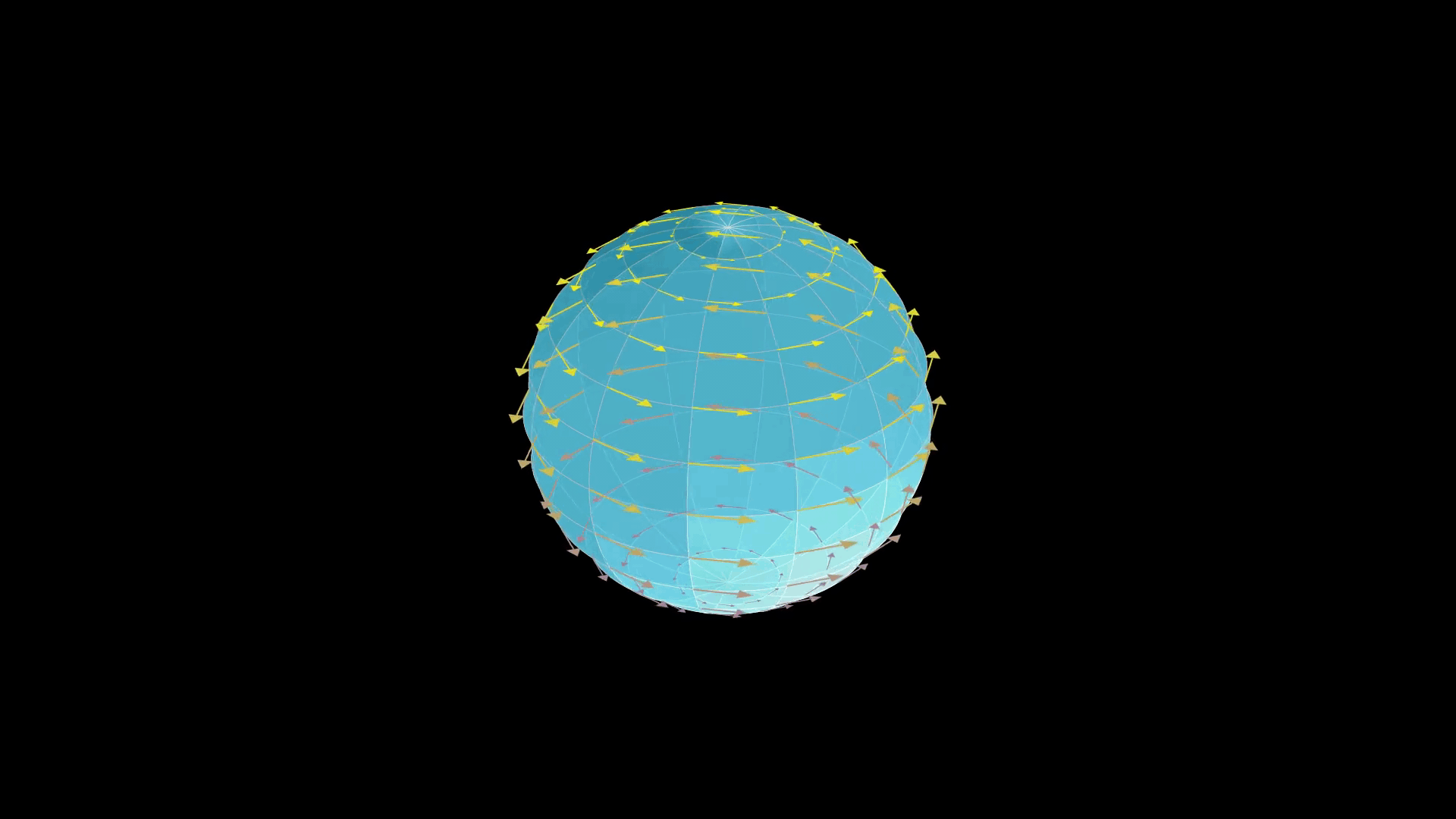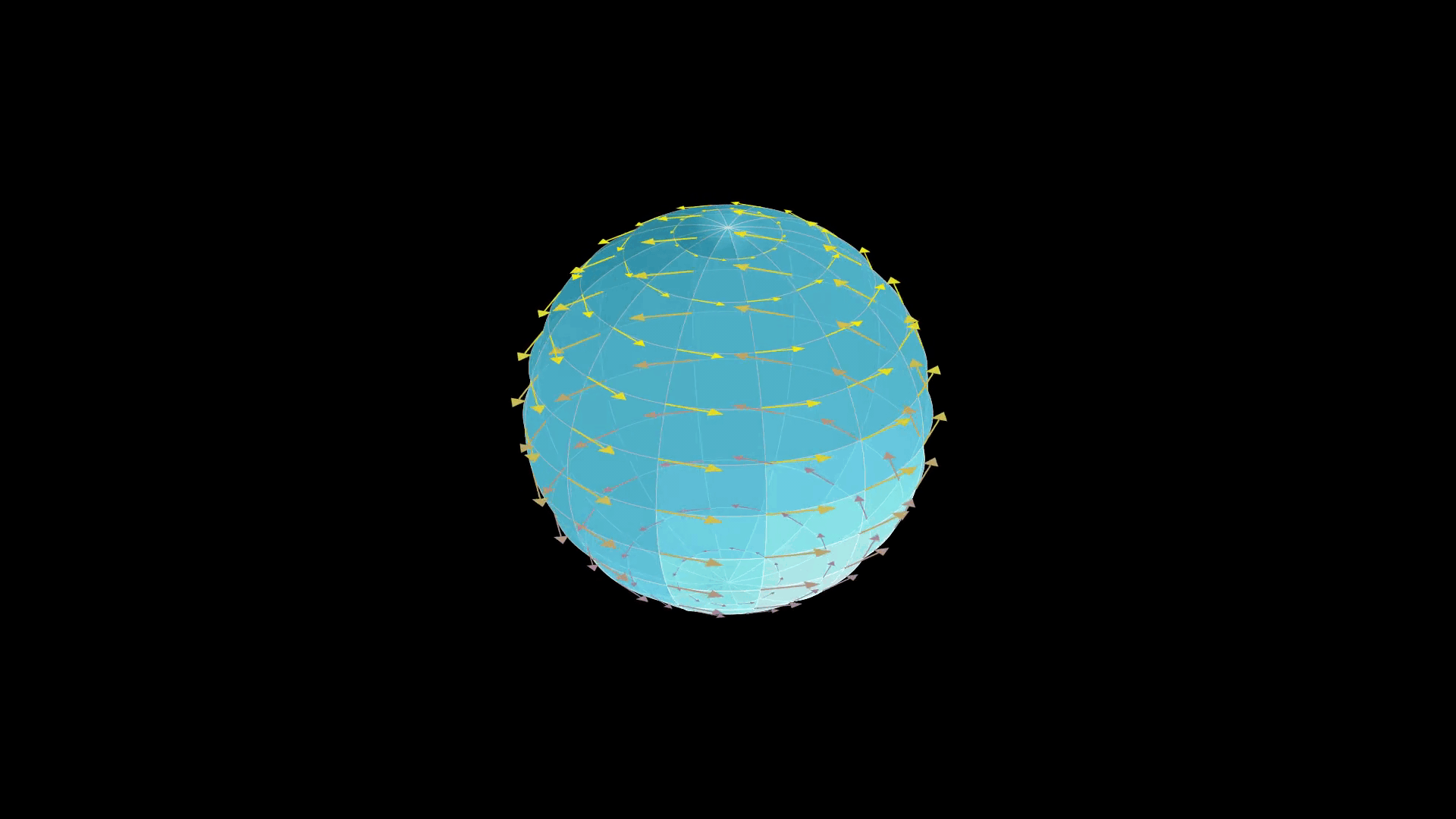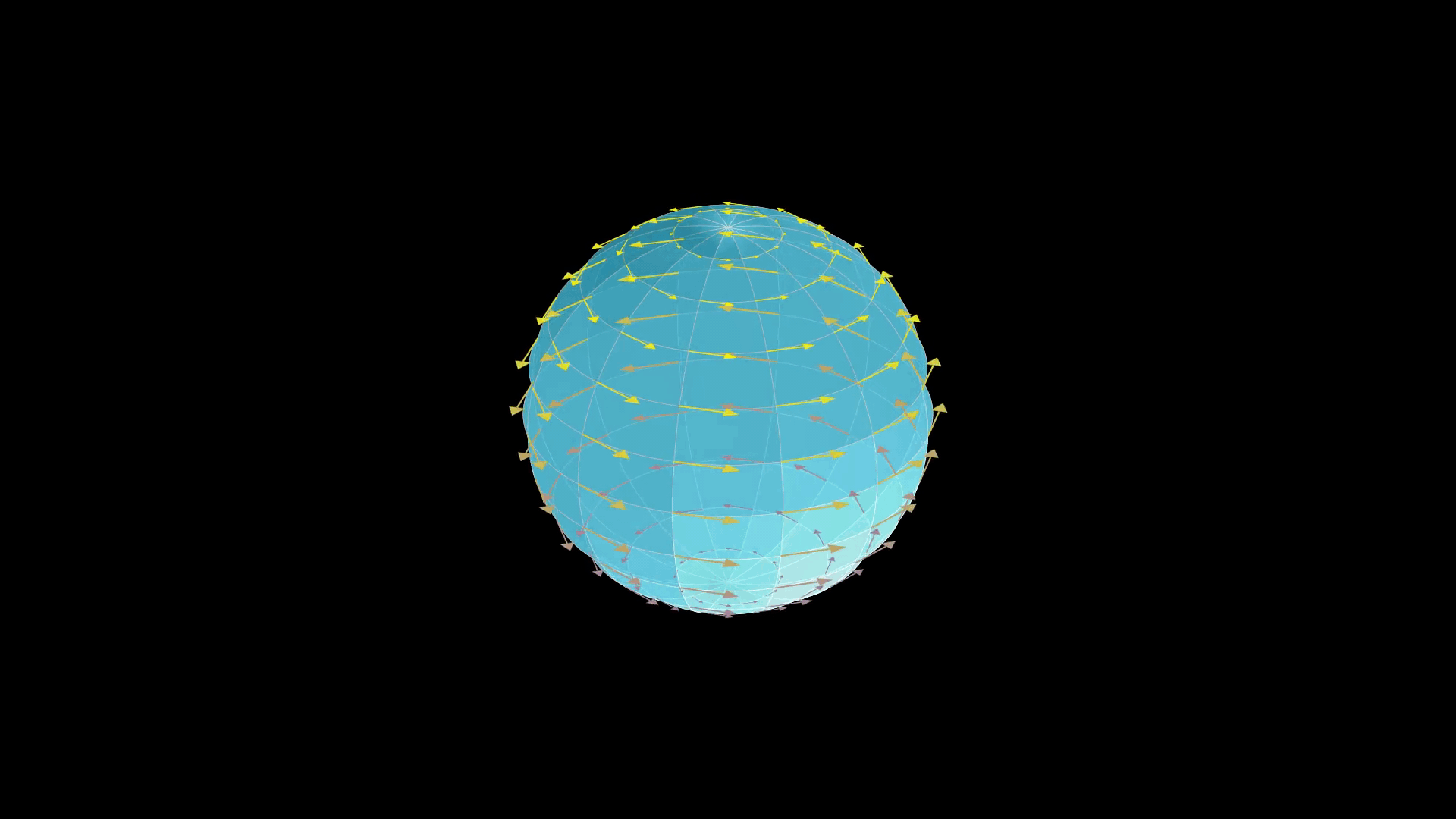 The Killing fields of the two-sphere , or more generally the -sphere should be "obvious" from ordinary intuition: spheres, having rotational symmetry, should possess Killing fields which generate rotations about any axis. That is, we expect to have symmetry under the action of the 3D rotation group
The Killing fields of the two-sphere , or more generally the -sphere should be "obvious" from ordinary intuition: spheres, having rotational symmetry, should possess Killing fields which generate rotations about any axis. That is, we expect to have symmetry under the action of the 3D rotation group
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a Killing vector field (often called a Killing field), named after Wilhelm Killing
Wilhelm Karl Joseph Killing (10 May 1847 – 11 February 1923) was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry.
Life
Killing studied at the University of Mü ...
, is a vector field on a Riemannian manifold
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real manifold, real, smooth manifold ''M'' equipped with a positive-definite Inner product space, inner product ...
(or pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the ...
) that preserves the metric
Metric or metrical may refer to:
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
In mathema ...
. Killing fields are the infinitesimal generators of isometries
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' mea ...
; that is, flows generated by Killing fields are continuous isometries of the manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a n ...
. More simply, the flow generates a symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definit ...
, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object.
Definition
Specifically, a vector field ''X'' is a Killing field if theLie derivative
In differential geometry, the Lie derivative ( ), named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a tensor field (including scalar functions, vector fields and one-forms), along the flow defined by another vector fi ...
with respect to ''X'' of the metric ''g'' vanishes:
:
In terms of the Levi-Civita connection
In Riemannian or pseudo Riemannian geometry (in particular the Lorentzian geometry of general relativity), the Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold (i.e. affine connection) that preserves th ...
, this is
:
for all vectors ''Y'' and ''Z''. In local coordinates
Local coordinates are the ones used in a ''local coordinate system'' or a ''local coordinate space''. Simple examples:
* Houses. In order to work in a house construction, the measurements are referred to a control arbitrary point that will allow ...
, this amounts to the Killing equation
:
This condition is expressed in covariant form. Therefore, it is sufficient to establish it in a preferred coordinate system in order to have it hold in all coordinate systems.
Examples
Killing field on the circle
 The vector field on a circle that points clockwise and has the same length at each point is a Killing vector field, since moving each point on the circle along this vector field simply rotates the circle.
The vector field on a circle that points clockwise and has the same length at each point is a Killing vector field, since moving each point on the circle along this vector field simply rotates the circle.
Killing fields in flat space
Here we derive the Killing fields for general flat space. From Killing's equation and the Ricci identity for a covector , : (usingabstract index notation
Abstract index notation (also referred to as slot-naming index notation) is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeho ...
) where is the Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. ...
, the following identity may be proven for a Killing field :
:
When the base manifold is flat space, that is, Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics ther ...
or possibly Pseudo-Euclidean space In mathematics and theoretical physics, a pseudo-Euclidean space is a finite-dimensional real -space together with a non-degenerate quadratic form . Such a quadratic form can, given a suitable choice of basis , be applied to a vector , giving
q(x) ...
(as for Minkowski space), we can choose global flat coordinates such that in these coordinates, the Levi-Civita connection and hence Riemann curvature vanishes everywhere, giving
:
Integrating and imposing the Killing equation allows us to write the general solution to as
:
where is antisymmetric. By taking appropriate values of and , we get a basis for the generalised Poincaré algebra of isometries of flat space:
:
:
These generate pseudo-rotations (rotations and boosts) and translations respectively. Intuitively these preserve the (pseudo)-metric at each point.
For (Pseudo-)Euclidean space of total dimension, in total there are generators, making flat space maximally symmetric. This number is generic for maximally symmetric spaces. Maximally symmetric spaces can be considered as sub-manifolds of flat space, arising as surfaces of constant proper distance
:
which have O(p,q) symmetry. If the submanifold has dimension , this group of symmetries has the expected dimension (as a Lie group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additio ...
).
Heuristically, we can derive the dimension of the Killing field algebra. Treating Killing's equation together with the identity as a system of second order differential equations for , we can determine the value of at any point given initial data at a point . The initial data specifies and , but Killing's equation imposes that the covariant derivative is antisymmetric. In total this is independent values of initial data.
For concrete examples, see below for examples of flat space (Minkowski space) and maximally symmetric spaces (sphere, hyperbolic space).
Killing fields on the hyperbolic plane
 A toy example for a Killing vector field is on the
A toy example for a Killing vector field is on the upper half-plane
In mathematics, the upper half-plane, \,\mathcal\,, is the set of points in the Cartesian plane with > 0.
Complex plane
Mathematicians sometimes identify the Cartesian plane with the complex plane, and then the upper half-plane corresponds to t ...
equipped with the Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry ...
. The pair is typically called the hyperbolic plane
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P'' ...
and has Killing vector field (using standard coordinates). This should be intuitively clear since the covariant derivative transports the metric along an integral curve generated by the vector field (whose image is parallel to the x-axis).
Furthermore, the metric is independent of from which we can immediately conclude that is a Killing field using one of the results below in this article.
The isometry group of the upper half-plane model (or rather, the component connected to the identity) is (see Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H = \, together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry.
Equivalently the Poincaré ha ...
), and the other two Killing fields may be derived from considering the action of the generators of on the upper half-plane. The other two generating Killing fields are dilatation and the special conformal transformation
In projective geometry, a special conformal transformation is a linear fractional transformation that is ''not'' an affine transformation. Thus the generation of a special conformal transformation involves use of multiplicative inversion, which ...
.
Killing fields on a 2-sphere
 The Killing fields of the two-sphere , or more generally the -sphere should be "obvious" from ordinary intuition: spheres, having rotational symmetry, should possess Killing fields which generate rotations about any axis. That is, we expect to have symmetry under the action of the 3D rotation group
The Killing fields of the two-sphere , or more generally the -sphere should be "obvious" from ordinary intuition: spheres, having rotational symmetry, should possess Killing fields which generate rotations about any axis. That is, we expect to have symmetry under the action of the 3D rotation group SO(3)
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space \R^3 under the operation of composition.
By definition, a rotation about the origin is a tr ...
.
When explicitly expressed in terms of the standard coordinate chart In topology, a branch of mathematics, a topological manifold is a topological space that locally resembles real ''n''-dimensional Euclidean space. Topological manifolds are an important class of topological spaces, with applications throughout mathe ...
for , the Killing fields have a non-obvious structure that obscures their nature. This is articulated below. This "non-obvious" structure is generic to manifolds that are not spheres, and thus the 2-sphere provides a good toy model on which to explore the intuitive interpretation of Killing fields.
The conventional chart for the 2-sphere embedded in in Cartesian coordinates is given by
:
so that parametrises the height, and parametrises rotation about the -axis.
Pulling back the standard Cartesian metric to these coordinates gives the standard metric on the sphere,
:.
Intuitively, a rotation about any axis should be an isometry. In this chart, we can immediately write down the vector field which generates rotations about the -axis:
:
Note that in these coordinates, the metric components are all independent of , which is another way for us to see that is a Killing vector (see below).
Naïvely we might hope to find another Killing vector
:
The metric is dependent on , so we cannot immediately deduce that it is a Killing vector. In fact, explicitly evaluating Killing's equation reveals it is not a Killing field. Intuitively, the flow generated by moves points downwards. Near , points move apart, thus distorting the metric, and we can see it is not an isometry, and therefore not a Killing field.
Killing fields have the property that the Lie bracket
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identit ...
of two Killing fields is still a Killing field. Thus, the Killing fields on a manifold ''M'' form a Lie subalgebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identit ...
of vector fields on ''M''. For example, we may wish to compute the dimension of this algebra and its structure constants
In mathematics, the structure constants or structure coefficients of an algebra over a field are used to explicitly specify the product of two basis vectors in the algebra as a linear combination. Given the structure constants, the resulting prod ...
, and possibly identify the Lie algebra.
Since are a coordinate basis, their commutator vanishes. Unfortunately, as earlier mentioned, is not a Killing field. In these coordinates, it is difficult to guess other Killing fields.
We can realize the algebra of Killing fields by considering as an embedded manifold of , and work in orthonormal Cartesian coordinates where commutators will turn out to be straight-forward.
The generator is recognized as a rotation about the -axis
:
A second generator, rotations about the -axis, is
:
Commuting these two, one finds a third generator for rotations about the -axis
:
The algebra given by linear combinations of these three generators closes, and we have the relations
: We identify this as the Lie algebra
Expressing and in terms of spherical coordinates gives
:
and
:
We'd like to say these three Killing fields are a complete set of generators for the algebra. One way to see this is that as a submanifold of , its symmetries are a strict subset of those of . The symmetries of are generated by rotations and translations. This can be shown using Killing's equation. Translations do not preserve the unit sphere, but rotations do. Hence this is the complete set of generators of the algebra of Killing fields, which we can identify with the algebra of rotations.
Killing fields in Minkowski space
The Killing fields ofMinkowski space
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inerti ...
are the 3 space translations, time translation, three generators of rotations (the little group
In mathematics, a group action on a space is a group homomorphism of a given group into the group of transformations of the space. Similarly, a group action on a mathematical structure is a group homomorphism of a group into the automorphism g ...
) and the three generators of boosts. These are
* Time and space translations
*:
* Vector fields generating three rotations, often called the ''J'' generators,
*:
* Vector fields generating three boosts, the ''K'' generators,
*:
The boosts and rotations generate the Lorentz group
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicis ...
. Together with space-time translations, this forms the Lie algebra for the Poincaré group
The Poincaré group, named after Henri Poincaré (1906), was first defined by Hermann Minkowski (1908) as the group of Minkowski spacetime isometries. It is a ten-dimensional non-abelian Lie group that is of importance as a model in our und ...
.
Killing fields in general relativity
Killing fields are used to discuss isometries ingeneral relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
(in which the geometry of spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differen ...
as distorted by gravitational field
In physics, a gravitational field is a model used to explain the influences that a massive body extends into the space around itself, producing a force on another massive body. Thus, a gravitational field is used to explain gravitational phenome ...
s is viewed as a 4-dimensional pseudo-Riemannian
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the r ...
manifold). In a static configuration, in which nothing changes with time, the time vector will be a Killing vector, and thus the Killing field will point in the direction of forward motion in time. For example, the Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an
exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumpti ...
has four Killing fields: the metric is independent of , hence is a time-like Killing field. The other three are the three generators of rotations discussed above. The Kerr metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of ge ...
for a rotating black hole has only two Killing fields: the time-like field, and a field generating rotations about the axis of rotation of the black hole.
de Sitter space
In mathematical physics, ''n''-dimensional de Sitter space (often abbreviated to dS''n'') is a maximally symmetric Lorentzian manifold with constant positive scalar curvature. It is the Lorentzian analogue of an ''n''-sphere (with its canoni ...
and anti-de Sitter space
In mathematics and physics, ''n''-dimensional anti-de Sitter space (AdS''n'') is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872� ...
are maximally symmetric spaces, with the -dimensional versions of each possessing Killing fields.
Killing field of a constant coordinate
If the metric coefficients in some coordinate basis are independent of one of the coordinates , then is a Killing vector, where is theKronecker delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
\delta_ = \begin
0 &\text i \neq j, \\
1 &\ ...
.
To prove this, let us assume . Then and
Now let us look at the Killing condition
:
and from . The Killing condition becomes
:
that is , which is true.
* The physical meaning is, for example, that, if none of the metric coefficients is a function of time, the manifold must automatically have a time-like Killing vector.
* In layman's terms, if an object doesn't transform or "evolve" in time (when time passes), time passing won't change the measures of the object. Formulated like this, the result sounds like a tautology, but one has to understand that the example is very much contrived: Killing fields apply also to much more complex and interesting cases.
Conversely, if the metric admits a Killing field , then one can construct coordinates for which . These coordinates are constructed by taking a hypersurface such that is nowhere tangent to . Take coordinates on , then define local coordinates where denotes the parameter along the integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations.
Name
Integral curves are known by various other names, depending on the nature and interpreta ...
of based at on . In these coordinates, the Lie derivative reduces to the coordinate derivative, that is,
:
and by the definition of the Killing field the left-hand side vanishes.
Properties
A Killing field is determined uniquely by a vector at some point and its gradient (i.e. allcovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a different ...
s of the field at the point).
The Lie bracket
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identit ...
of two Killing fields is still a Killing field. The Killing fields on a manifold ''M'' thus form a Lie subalgebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identit ...
of vector fields on ''M''. This is the Lie algebra of the isometry group In mathematics, the isometry group of a metric space is the set of all bijective isometries (i.e. bijective, distance-preserving maps) from the metric space onto itself, with the function composition as group operation. Its identity element is the ...
of the manifold if ''M'' is complete
Complete may refer to:
Logic
* Completeness (logic)
* Completeness of a theory, the property of a theory that every formula in the theory's language or its negation is provable
Mathematics
* The completeness of the real numbers, which implies t ...
. A Riemannian manifold
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real manifold, real, smooth manifold ''M'' equipped with a positive-definite Inner product space, inner product ...
with a transitive group of isometries is a homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group ''G'' is a non-empty manifold or topological space ''X'' on which ''G'' acts transitively. The elements of ' ...
.
For compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact
* Blood compact, an ancient ritual of the Philippines
* Compact government, a type of colonial rule utilized in British ...
manifolds
* Negative Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure ...
implies there are no nontrivial (nonzero) Killing fields.
* Nonpositive Ricci curvature implies that any Killing field is parallel. i.e. covariant derivative along any vector field is identically zero.
* If the sectional curvature In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature ''K''(σ''p'') depends on a two-dimensional linear subspace σ''p'' of the tangent space at a poi ...
is positive and the dimension of ''M'' is even, a Killing field must have a zero.
The covariant divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the ...
of every Killing vector field vanishes.
If is a Killing vector field and is a harmonic vector field, then is a harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f: U \to \mathbb R, where is an open subset of that satisfies Laplace's equation, that is,
: \f ...
.
If is a Killing vector field and is a harmonic p-form, then
Geodesics
Each Killing vector corresponds to a quantity which is conserved alonggeodesics
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. ...
. This conserved quantity is the metric product between the Killing vector and the geodesic tangent vector. Along an affinely parametrized geodesic with tangent vector then given the Killing vector , the quantity is conserved:
:
This aids in analytically studying motions in a spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differen ...
with symmetries.
Stress-energy tensor
Given a conserved, symmetric tensor , that is, one satisfying and , which are properties typical of a stress-energy tensor, and a Killing vector , we can construct the conserved quantity satisfying :Cartan decomposition
As noted above, theLie bracket
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identit ...
of two Killing fields is still a Killing field. The Killing fields on a manifold thus form a Lie subalgebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identit ...
of all vector fields on Selecting a point the algebra can be decomposed into two parts:
:
and
:
where is the covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a different ...
. These two parts intersect trivially but do not in general split . For instance, if is a Riemannian homogeneous space, we have if and only if is a Riemannian symmetric space.
Intuitively, the isometries of locally define a submanifold of the total space, and the Killing fields show how to "slide along" that submanifold. They span the tangent space of that submanifold. The tangent space should have the same dimension as the isometries acting effectively at that point. That is, one expects Yet, in general, the number of Killing fields is larger than the dimension of that tangent space. How can this be? The answer is that the "extra" Killing fields are redundant. Taken all together, the fields provide an over-complete basis for the tangent space at any particular selected point; linear combinations can be made to vanish at that particular point. This was seen in the example of the Killing fields on a 2-sphere: there are 3 Killing fields; at any given point, two span the tangent space at that point, and the third one is a linear combination of the other two. Picking any two defines the remaining degenerate linear combinations define an orthogonal space
Cartan involution
TheCartan involution
In mathematics, the Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition or singular value decom ...
is defined as the mirroring or reversal of the direction of a geodesic. Its differential flips the direction of the tangents to a geodesic. It is a linear operator of norm one; it has two invariant subspaces, of eigenvalue +1 and −1. These two subspaces correspond to and respectively.
This can be made more precise. Fixing a point consider a geodesic passing through , with The involution
Involution may refer to:
* Involute, a construction in the differential geometry of curves
* '' Agricultural Involution: The Processes of Ecological Change in Indonesia'', a 1963 study of intensification of production through increased labour inpu ...
is defined as
:
This map is an involution, in that When restricted to geodesics along the Killing fields, it is also clearly an isometry. It is uniquely defined.
Let be the group of isometries generated by the Killing fields. The function defined by
:
is a homomorphism
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type (such as two groups, two rings, or two vector spaces). The word ''homomorphism'' comes from the Ancient Greek language: () meaning "same" ...
of . Its infinitesimal is
:
The Cartan involution is a Lie algebra homomorphism, in that
: