|
Killing Tensor
In mathematics, a Killing tensor or Killing tensor field is a generalization of a Killing vector, for symmetric tensor fields instead of just vector fields. It is a concept in pseudo-Riemannian geometry, and is mainly used in the theory of general relativity. Killing tensors satisfy an equation similar to Killing's equation for Killing vectors. Like Killing vectors, every Killing tensor corresponds to a quantity which is conserved along geodesics. However, unlike Killing vectors, which are associated with symmetries (isometries) of a manifold, Killing tensors generally lack such a direct geometric interpretation. Killing tensors are named after Wilhelm Killing. Definition and properties In the following definition, parentheses around tensor indices are notation for symmetrization. For example: :T_ = \frac(T_ + T_ + T_ + T_ + T_ + T_) Definition A Killing tensor is a tensor field K (of some order ''m'') on a (pseudo)-Riemannian manifold which is symmetric (that is, K_ = K_) and sat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Killing Vector
In mathematics, a Killing vector field (often called a Killing field), named after Wilhelm Killing, is a vector field on a Riemannian manifold (or pseudo-Riemannian manifold) that preserves the metric tensor, metric. Killing fields are the Lie group#The Lie algebra associated to a Lie group, infinitesimal generators of isometry, isometries; that is, flow (geometry), flows generated by Killing fields are Isometry (Riemannian geometry), continuous isometries of the manifold. More simply, the flow generates a symmetry, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object. Definition Specifically, a vector field ''X'' is a Killing field if the Lie derivative with respect to ''X'' of the metric ''g'' vanishes: :\mathcal_ g = 0 \,. In terms of the Levi-Civita connection, this is :g\left(\nabla_Y X, Z\right) + g\left(Y, \nabla_Z X\right) = 0 \, for all vectors ''Y'' and ''Z''. In local coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Friedmann–Lemaître–Robertson–Walker Metric
The Friedmann–Lemaître–Robertson–Walker (FLRW; ) metric is a metric based on the exact solution of Einstein's field equations of general relativity; it describes a homogeneous, isotropic, expanding (or otherwise, contracting) universe that is path-connected, but not necessarily simply connected. The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, the set of the four scientists – Alexander Friedmann, Georges Lemaître, Howard P. Robertson and Arthur Geoffrey Walker – are customarily grouped as Friedmann or Friedmann–Robertson–Walker (FRW) or Robertson–Walker (RW) or Friedmann–Lemaître (FL). This model is sometimes called the ''Standard Model'' of modern cosmology, although such a description is also associated with the further developed Lambda-CDM model. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Killing Form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras. Cartan's criteria (criterion of solvability and criterion of semisimplicity) show that Killing form has a close relationship to the semisimplicity of the Lie algebras. History and name The Killing form was essentially introduced into Lie algebra theory by in his thesis. In a historical survey of Lie theory, has described how the term ''"Killing form"'' first occurred in 1951 during one of his own reports for the Séminaire Bourbaki; it arose as a misnomer, since the form had previously been used by Lie theorists, without a name attached. Some other authors now employ the term ''" Cartan-Killing form"''. At the end of the 19th century, Killing had noted that the coefficients of the characteristic equation of a regular semisimple element of a Lie algebra are invariant under the adjoint group, from which it follows tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariant Derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component (dependent on the embedding) and the intrinsic covariant derivative component. The name is motivated by the importance of changes of coordinate in physics: the covariant derivative transforms covariantly under a general coordinate transformation, that is, linearly via the Jacobia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carter Constant
The Carter constant is a conserved quantity for motion around black holes in the general relativistic formulation of gravity. Its SI base units are kg2⋅m4⋅s−2. Carter's constant was derived for a spinning, charged black hole by Australian theoretical physicist Brandon Carter in 1968. Carter's constant along with the energy, axial angular momentum, and particle rest mass provide the four conserved quantities necessary to uniquely determine all orbits in the Kerr–Newman spacetime (even those of charged particles). Formulation Carter noticed that the Hamiltonian for motion in Kerr spacetime was separable in Boyer–Lindquist coordinates, allowing the constants of such motion to be easily identified using Hamilton–Jacobi theory. The Carter constant can be written as follows: :C = p_^ + \cos^\theta \Bigg( a^(m^ - E^) + \left(\frac \right)^ \Bigg), where p_ is the latitudinal component of the particle's angular momentum, E is the energy of the particle, L_z is the par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roger Penrose
Sir Roger Penrose (born 8 August 1931) is an English mathematician, mathematical physicist, philosopher of science and Nobel Laureate in Physics. He is Emeritus Rouse Ball Professor of Mathematics in the University of Oxford, an emeritus fellow of Wadham College, Oxford, and an honorary fellow of St John's College, Cambridge and University College London. Penrose has contributed to the mathematical physics of general relativity and cosmology. He has received several prizes and awards, including the 1988 Wolf Prize in Physics, which he shared with Stephen Hawking for the Penrose–Hawking singularity theorems, and one half of the 2020 Nobel Prize in Physics "for the discovery that black hole formation is a robust prediction of the general theory of relativity". He is regarded as one of the greatest living physicists, mathematicians and scientists, and is particularly noted for the breadth and depth of his work in both natural and formal sciences. Early life and education Bor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Symmetry
Axial symmetry is symmetry around an axis; an object is axially symmetric if its appearance is unchanged if rotated around an axis. glossary of meteorology. Retrieved 2010-04-08. For example, a without trademark or other design, or a plain white tea saucer, looks the same if it is rotated by any angle about the line passing lengthwise through its center, so it is axially symmetric. Axial symmetry can also be |
Time Translation Symmetry
Time translation symmetry or temporal translation symmetry (TTS) is a mathematical transformation in physics that moves the times of events through a common interval. Time translation symmetry is the law that the laws of physics are unchanged (i.e. invariant) under such a transformation. Time translation symmetry is a rigorous way to formulate the idea that the laws of physics are the same throughout history. Time translation symmetry is closely connected, via the Noether theorem, to conservation of energy. In mathematics, the set of all time translations on a given system form a Lie group. There are many symmetries in nature besides time translation, such as spatial translation or rotational symmetries. These symmetries can be broken and explain diverse phenomena such as crystals, superconductivity, and the Higgs mechanism. However, it was thought until very recently that time translation symmetry could not be broken. Time crystals, a state of matter first observed in 201 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
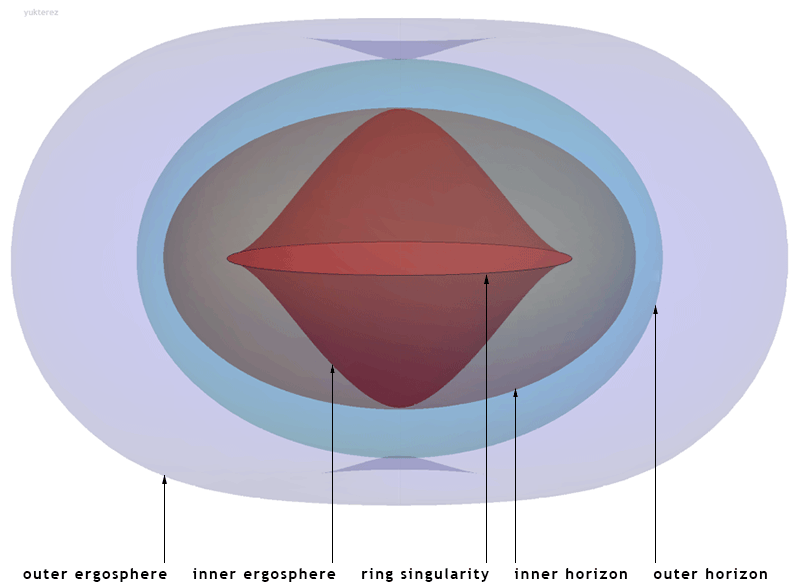
Kerr Metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of black ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Signature
In mathematics, the signature of a metric tensor ''g'' (or equivalently, a real quadratic form thought of as a real symmetric bilinear form on a finite-dimensional vector space) is the number (counted with multiplicity) of positive, negative and zero eigenvalues of the real symmetric matrix of the metric tensor with respect to a basis. In relativistic physics, the ''v'' represents the time or virtual dimension, and the ''p'' for the space and physical dimension. Alternatively, it can be defined as the dimensions of a maximal positive and null subspace. By Sylvester's law of inertia these numbers do not depend on the choice of basis. The signature thus classifies the metric up to a choice of basis. The signature is often denoted by a pair of integers implying ''r''= 0, or as an explicit list of signs of eigenvalues such as or for the signatures and , respectively. The signature is said to be indefinite or mixed if both ''v'' and ''p'' are nonzero, and degenerate if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Factor (cosmology)
The relative expansion of the universe is parametrized by a dimensionless scale factor a . Also known as the cosmic scale factor or sometimes the Robertson Walker scale factor, this is a key parameter of the Friedmann equations. In the early stages of the Big Bang, most of the energy was in the form of radiation, and that radiation was the dominant influence on the expansion of the universe. Later, with cooling from the expansion the roles of matter and radiation changed and the universe entered a matter-dominated era. Recent results suggest that we have already entered an era dominated by dark energy, but examination of the roles of matter and radiation are most important for understanding the early universe. Using the dimensionless scale factor to characterize the expansion of the universe, the effective energy densities of radiation and matter scale differently. This leads to a radiation-dominated era in the very early universe but a transition to a matter-dominated era at a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |