|
Covariant Derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component (dependent on the embedding) and the intrinsic covariant derivative component. The name is motivated by the importance of changes of coordinate in physics: the covariant derivative transforms covariantly under a general coordinate transformation, that is, linearly via the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauge Theory
In physics, a gauge theory is a type of field theory in which the Lagrangian (and hence the dynamics of the system itself) does not change (is invariant) under local transformations according to certain smooth families of operations (Lie groups). The term ''gauge'' refers to any specific mathematical formalism to regulate redundant degrees of freedom in the Lagrangian of a physical system. The transformations between possible gauges, called ''gauge transformations'', form a Lie group—referred to as the ''symmetry group'' or the ''gauge group'' of the theory. Associated with any Lie group is the Lie algebra of group generators. For each group generator there necessarily arises a corresponding field (usually a vector field) called the ''gauge field''. Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (called ''gauge invariance''). When such a theory is quantized, the quanta of the gauge fields are called '' gauge boson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Matrix And Determinant
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian in literature. Suppose is a function such that each of its first-order partial derivatives exist on . This function takes a point as input and produces the vector as output. Then the Jacobian matrix of is defined to be an matrix, denoted by , whose th entry is \mathbf J_ = \frac, or explicitly :\mathbf J = \begin \dfrac & \cdots & \dfrac \end = \begin \nabla^ f_1 \\ \vdots \\ \nabla^ f_m \end = \begin \dfrac & \cdots & \dfrac\\ \vdots & \ddots & \vdots\\ \dfrac & \cd ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crelle's Journal
''Crelle's Journal'', or just ''Crelle'', is the common name for a mathematics journal, the ''Journal für die reine und angewandte Mathematik'' (in English: ''Journal for Pure and Applied Mathematics''). History The journal was founded by August Leopold Crelle (Berlin) in 1826 and edited by him until his death in 1855. It was one of the first major mathematical journals that was not a proceedings of an academy. It has published many notable papers, including works of Niels Henrik Abel, Georg Cantor, Gotthold Eisenstein, Carl Friedrich Gauss and Otto Hesse. It was edited by Carl Wilhelm Borchardt from 1856 to 1880, during which time it was known as ''Borchardt's Journal''. The current editor-in-chief is Rainer Weissauer ( Ruprecht-Karls-Universität Heidelberg) Past editors * 1826–1856 August Leopold Crelle * 1856–1880 Carl Wilhelm Borchardt * 1881–1888 Leopold Kronecker, Karl Weierstrass * 1889–1892 Leopold Kronecker * 1892–1902 Lazarus Fuchs * 1903–19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
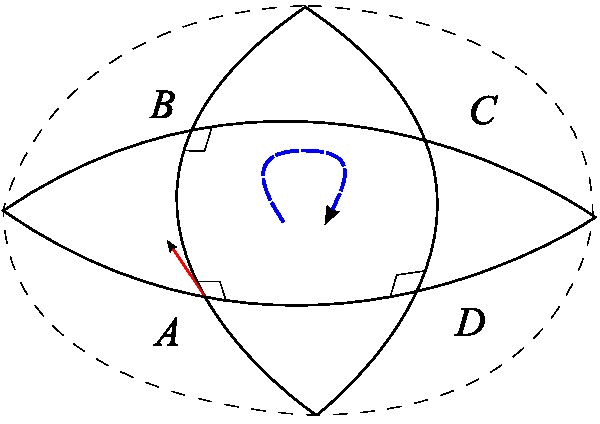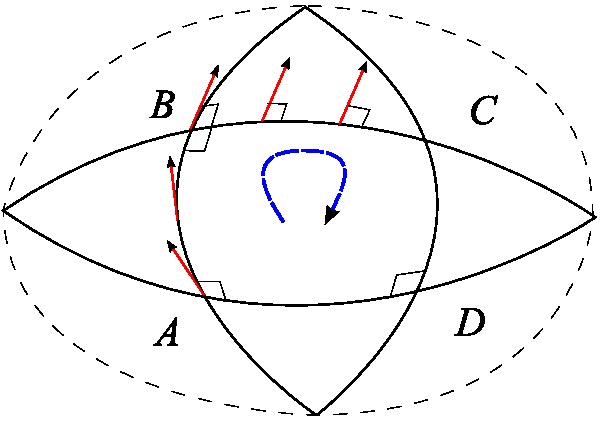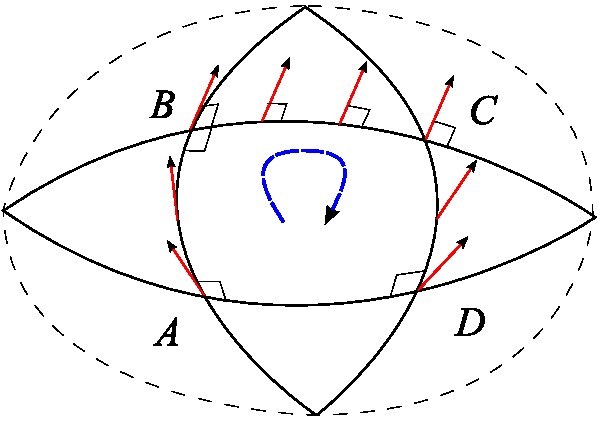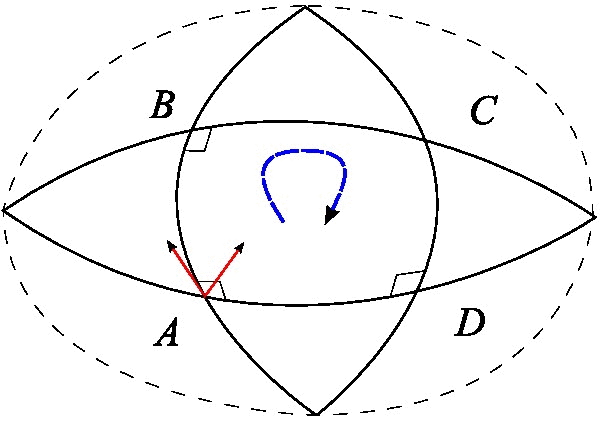
Riemann Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Christoffel Symbols
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing distances to be measured on that surface. In differential geometry, an affine connection can be defined without reference to a metric, and many additional concepts follow: parallel transport, covariant derivatives, geodesics, etc. also do not require the concept of a metric. However, when a metric is available, these concepts can be directly tied to the "shape" of the manifold itself; that shape is determined by how the tangent space is attached to the cotangent space by the metric tensor. Abstractly, one would say that the manifold has an associated (orthonormal) frame bundle, with each " frame" being a possible choice of a coordinate frame. An invariant metric implies that the structure group of the frame bundle is the orthogonal group . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elwin Bruno Christoffel
Elwin Bruno Christoffel (; 10 November 1829 – 15 March 1900) was a German mathematician and physicist. He introduced fundamental concepts of differential geometry, opening the way for the development of tensor calculus, which would later provide the mathematical basis for general relativity. Life Christoffel was born on 10 November 1829 in Montjoie (now Monschau) in Prussia in a family of cloth merchants. He was initially educated at home in languages and mathematics, then attended the Jesuit Gymnasium and the Friedrich-Wilhelms Gymnasium in Cologne. In 1850 he went to the University of Berlin, where he studied mathematics with Gustav Dirichlet (which had a strong influence over him) among others, as well as attending courses in physics and chemistry. He received his doctorate in Berlin in 1856 for a thesis on the motion of electricity in homogeneous bodies written under the supervision of Martin Ohm, Ernst Kummer and Heinrich Gustav Magnus. After receiving his doctorate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-Riemannian Manifold
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of positive-definiteness is relaxed. Every tangent space of a pseudo-Riemannian manifold is a pseudo-Euclidean vector space. A special case used in general relativity is a four-dimensional Lorentzian manifold for modeling spacetime, where tangent vectors can be classified as timelike, null, and spacelike. Introduction Manifolds In differential geometry, a differentiable manifold is a space which is locally similar to a Euclidean space. In an ''n''-dimensional Euclidean space any point can be specified by ''n'' real numbers. These are called the coordinates of the point. An ''n''-dimensional differentiable manifold is a generalisation of ''n''-dimensional Euclidean space. In a manifold it may only be possibl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemannian Geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions. Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugural lecture "''Ueber die Hypothesen, welche der Geometrie zu Grunde liegen''" ("On the Hypotheses on which Geometry is Based.") It is a very broad and abstract generalization of the differential geometry of surfaces in R3. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics on them, with techniques that can be applied to the study of differentiable manifolds of higher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tullio Levi-Civita
Tullio Levi-Civita, (, ; 29 March 1873 – 29 December 1941) was an Italian mathematician, most famous for his work on absolute differential calculus ( tensor calculus) and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus. His work included foundational papers in both pure and applied mathematics, celestial mechanics (notably on the three-body problem), analytic mechanics (the Levi-Civita separability conditions in the Hamilton–Jacobi equation) and hydrodynamics. Biography Born into an Italian Jewish family in Padua, Levi-Civita was the son of Giacomo Levi-Civita, a lawyer and former senator. He graduated in 1892 from the University of Padua Faculty of Mathematics. In 1894 he earned a teaching diploma after which he was appointed to the Faculty of Science teacher's college in Pavia. In 1898 he was appointed to the Padua Chair of Rational Mec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro (; 12January 1925) was an Italian mathematician. He is most famous as the discoverer of tensor calculus. With his former student Tullio Levi-Civita, he wrote his most famous single publication, a pioneering work on the calculus of tensors, signing it as Gregorio Ricci. This appears to be the only time that Ricci-Curbastro used the shortened form of his name in a publication, and continues to cause confusion. Ricci-Curbastro also published important works in other fields, including a book on higher algebra and infinitesimal analysis, and papers on the theory of real numbers, an area in which he extended the research begun by Richard Dedekind. Early life and education Completing privately his high school studies at only 16 years of age, he enrolled on the course of philosophy-mathematics at Rome University (1869). The following year the Papal State fell and so Gregorio was called by his father to the city of his birth, Lugo di Romagna. Subsequently he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connection On A Vector Bundle
In mathematics, and especially differential geometry and gauge theory, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. The most common case is that of a linear connection on a vector bundle, for which the notion of parallel transport must be linear. A linear connection is equivalently specified by a ''covariant derivative'', an operator that differentiates sections of the bundle along tangent directions in the base manifold, in such a way that parallel sections have derivative zero. Linear connections generalize, to arbitrary vector bundles, the Levi-Civita connection on the tangent bundle of a pseudo-Riemannian manifold, which gives a standard way to differentiate vector fields. Nonlinear connections generalize this concept to bundles whose fibers are not necessarily linear. Linear connections are also called Koszul connections after Jean-Louis Koszul, who ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |