History Of The Hindu–Arabic Numeral System on:
[Wikipedia]
[Google]
[Amazon]
The
 The form of numerals in
The form of numerals in
 While the numerals in texts and inscriptions used a named place-value notation, a more efficient notation might have been employed in calculations, possibly from the 1st century CE. Computations were carried out on clay tablets covered with a thin layer of sand, giving rise to the term ''dhuli-karana'' ('sand-work') for higher computation. Karl Menninger believes that, in such computations, they must have dispensed with the enciphered numerals and written down just sequences of digits to represent the numbers. A zero would have been represented as a "missing place", such as a dot. The single manuscript with worked examples available to us, the Bakhshali manuscript (of unclear date), uses a place value system with a dot to denote the zero. The dot was called the ''shunya-sthāna'' 'empty-place'. The same symbol was also used in algebraic expressions for the unknown (as in the canonical ''x'' in modern algebra).
Textual references to a place-value system are seen from the 5th century CE onward. A commentary on
While the numerals in texts and inscriptions used a named place-value notation, a more efficient notation might have been employed in calculations, possibly from the 1st century CE. Computations were carried out on clay tablets covered with a thin layer of sand, giving rise to the term ''dhuli-karana'' ('sand-work') for higher computation. Karl Menninger believes that, in such computations, they must have dispensed with the enciphered numerals and written down just sequences of digits to represent the numbers. A zero would have been represented as a "missing place", such as a dot. The single manuscript with worked examples available to us, the Bakhshali manuscript (of unclear date), uses a place value system with a dot to denote the zero. The dot was called the ''shunya-sthāna'' 'empty-place'. The same symbol was also used in algebraic expressions for the unknown (as in the canonical ''x'' in modern algebra).
Textual references to a place-value system are seen from the 5th century CE onward. A commentary on
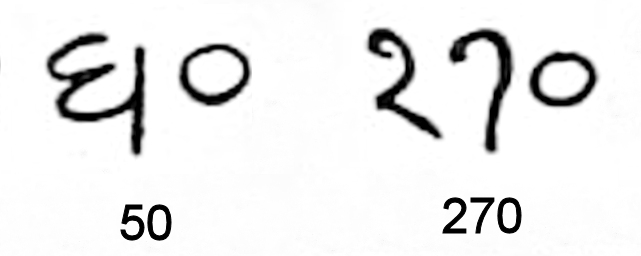 In 628 CE, astronomer-mathematician
In 628 CE, astronomer-mathematician
File:Houghton Typ 520.03.736 - Margarita philosophica.jpg
File:Rechentisch.png
File:Rechnung auff der Linihen und Federn.JPG
File:Köbel Böschenteyn 1514.jpg
File:Rechnung auff der linihen 1525 Adam Ries.PNG
File:1543 Robert Recorde.PNG
File:Peter Apian 1544.PNG
File:Adam riesen.jpg
1482 Ptolemaeus map of the world
printed by Lienhart Holle in Ulm, and other examples in the Gutenberg Museum in
"The Development of Hindu–Arabic and Traditional Chinese Arithmetic" by Professor Lam Lay Yong, member of the International Academy of the History of Science
* {{DEFAULTSORT:History Of The Hindi-Arabic Numeral System Numeral systems Elementary mathematics Arabic language History of science and technology in India
Hindu–Arabic numeral system
The Hindu–Arabic numeral system (also known as the Indo-Arabic numeral system, Hindu numeral system, and Arabic numeral system) is a positional notation, positional Decimal, base-ten numeral system for representing integers; its extension t ...
is a decimal place-value numeral system that uses a zero
0 (zero) is a number representing an empty quantity. Adding (or subtracting) 0 to any number leaves that number unchanged; in mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and compl ...
glyph as in "205".
Its glyphs are descended from the Indian Brahmi numerals
Brahmi numerals are a numeral system attested in the Indian subcontinent from the 3rd century BCE. It is the direct graphic ancestor of the modern Hindu–Arabic numeral system. However, the Brahmi numeral system was conceptually distinct from ...
. The full system emerged by the 8th to 9th centuries, and is first described outside India in Al-Khwarizmi
Muhammad ibn Musa al-Khwarizmi , or simply al-Khwarizmi, was a mathematician active during the Islamic Golden Age, who produced Arabic-language works in mathematics, astronomy, and geography. Around 820, he worked at the House of Wisdom in B ...
's ''On the Calculation with Hindu Numerals'' (ca. 825), and second Al-Kindi
Abū Yūsuf Yaʻqūb ibn ʼIsḥāq aṣ-Ṣabbāḥ al-Kindī (; ; ; ) was an Arab Muslim polymath active as a philosopher, mathematician, physician, and music theorist
Music theory is the study of theoretical frameworks for understandin ...
's four-volume work ''On the Use of the Indian Numerals'' (ca. 830). Today the name ''Hindu–Arabic numerals'' is usually used.
Decimal system
Historians trace modern numerals in most languages to the Brahmi numerals, which were in use around the middle of the 3rd century BC. Theplace value
Place may refer to:
Geography
* Place (United States Census Bureau), defined as any concentration of population
** Census-designated place, a populated area lacking its own municipal government
* "Place", a type of street or road name
** O ...
system, however, developed later. The Brahmi numerals have been found in inscriptions in caves and on coins in regions near Pune, Maharashtra
Pune ( ; , ISO 15919, ISO: ), previously spelled in English as Poona (List of renamed Indian cities and states#Maharashtra, the official name until 1978), is a city in the state of Maharashtra in the Deccan Plateau, Deccan plateau in Western ...
and Uttar Pradesh
Uttar Pradesh ( ; UP) is a States and union territories of India, state in North India, northern India. With over 241 million inhabitants, it is the List of states and union territories of India by population, most populated state in In ...
in India. These numerals (with slight variations) were in use up to the 4th century.
During the Gupta period
The Gupta Empire was an Indian empire during the classical period of the Indian subcontinent which existed from the mid 3rd century to mid 6th century CE. At its zenith, the dynasty ruled over an empire that spanned much of the northern Indian ...
(early 4th century to the late 6th century), the Gupta numerals developed from the Brahmi numerals and were spread over large areas by the Gupta empire as they conquered territory. Beginning around 7th century, the Gupta numerals developed into the Nagari numerals.
Development in India
During theVedic period
The Vedic period, or the Vedic age (), is the period in the late Bronze Age and early Iron Age of the history of India when the Vedic literature, including the Vedas (–900 BCE), was composed in the northern Indian subcontinent, between the e ...
(1500–500 BCE), motivated by geometric construction of the fire altars and astronomy, the use of a numerical system and of basic mathematical operations developed in northern India. Hindu cosmology required the mastery of very large numbers such as the ''kalpa'' (the lifetime of the universe) said to be 4,320,000,000 years and the "orbit of the heaven" said to be 18,712,069,200,000,000 ''yojanas''. Numbers were expressed using a "named place-value notation", using names for the powers of 10, like ''dasa'', ''shatha'', ''sahasra'', ''ayuta'', ''niyuta'', ''prayuta'', ''arbuda'', ''nyarbuda'', ''samudra'', ''madhya'', ''anta'', ''parardha'' etc., the last of these being the name for a trillion (1012). For example, the number 26,432 was expressed as "2 ''ayuta'', 6 ''sahasra'', 4 ''shatha'', 3 ''dasa'', 2." In the Buddhist text Lalitavistara, the Buddha is said to have narrated a scheme of numbers up to 1053.
 The form of numerals in
The form of numerals in Ashoka
Ashoka, also known as Asoka or Aśoka ( ; , ; – 232 BCE), and popularly known as Ashoka the Great, was List of Mauryan emperors, Emperor of Magadha from until #Death, his death in 232 BCE, and the third ruler from the Mauryan dynast ...
's inscriptions in the Brahmi
Brahmi ( ; ; ISO: ''Brāhmī'') is a writing system from ancient India. "Until the late nineteenth century, the script of the Aśokan (non-Kharosthi) inscriptions and its immediate derivatives was referred to by various names such as 'lath' or ...
script (middle of the third century BCE) involved separate signs for the numbers 1 to 9, 10 to 90, 100 and 1000. A multiple of 100 or 1000 was represented by a modification (or "enciphering") of the sign for the number using the sign for the multiplier number. Such enciphered numerals directly represented the named place-value numerals used verbally. They continued to be used in inscriptions until the end of the 9th century.
In his seminal text of 499 CE, Aryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was the first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy. His works include the '' Āryabhaṭīya'' (which mentions that in 3600 ' ...
devised a novel positional number system, using Sanskrit consonants for small numbers and vowels for powers of 10. Using the system, numbers up to a billion could be expressed using short phrases, e. g., ''khyu-ghṛ'' representing the number 4,320,000. The system did not catch on because it produced quite unpronounceable phrases, but it might have driven home the principle of positional number system (called ''dasa-gunottara'', exponents of 10) to later mathematicians. A more elegant ''katapayadi'' scheme was devised in later centuries representing a place-value system including zero.
Place-value numerals without zero
 While the numerals in texts and inscriptions used a named place-value notation, a more efficient notation might have been employed in calculations, possibly from the 1st century CE. Computations were carried out on clay tablets covered with a thin layer of sand, giving rise to the term ''dhuli-karana'' ('sand-work') for higher computation. Karl Menninger believes that, in such computations, they must have dispensed with the enciphered numerals and written down just sequences of digits to represent the numbers. A zero would have been represented as a "missing place", such as a dot. The single manuscript with worked examples available to us, the Bakhshali manuscript (of unclear date), uses a place value system with a dot to denote the zero. The dot was called the ''shunya-sthāna'' 'empty-place'. The same symbol was also used in algebraic expressions for the unknown (as in the canonical ''x'' in modern algebra).
Textual references to a place-value system are seen from the 5th century CE onward. A commentary on
While the numerals in texts and inscriptions used a named place-value notation, a more efficient notation might have been employed in calculations, possibly from the 1st century CE. Computations were carried out on clay tablets covered with a thin layer of sand, giving rise to the term ''dhuli-karana'' ('sand-work') for higher computation. Karl Menninger believes that, in such computations, they must have dispensed with the enciphered numerals and written down just sequences of digits to represent the numbers. A zero would have been represented as a "missing place", such as a dot. The single manuscript with worked examples available to us, the Bakhshali manuscript (of unclear date), uses a place value system with a dot to denote the zero. The dot was called the ''shunya-sthāna'' 'empty-place'. The same symbol was also used in algebraic expressions for the unknown (as in the canonical ''x'' in modern algebra).
Textual references to a place-value system are seen from the 5th century CE onward. A commentary on Patanjali
Patanjali (, , ; also called Gonardiya or Gonikaputra) was the name of one or more author(s), mystic(s) and philosopher(s) in ancient India. His name is recorded as an author and compiler of a number of Sanskrit works. The greatest of these a ...
's Yoga Sutras
The ''Yoga Sutras of Patañjali'' (IAST: Patañjali yoga-sūtra) is a compilation "from a variety of sources" of Sanskrit sutras (aphorisms) on the practice of yoga – 195 sutras (according to Vyasa, Vyāsa and Krishnamacharya) and 196 sut ...
from the 5th century reads, "Just as a line in the hundreds place eansa hundred, in the tens place ten, and one in the ones place, so one and the same woman is called mother, daughter and sister."
A system called ''bhūta-sankhya'' ('object numbers' or 'concrete numbers') was employed for representing numerals in Sanskrit verses, by using a concept representing a digit to stand for the digit itself. The Jain text entitled the ''Lokavibhaga
The ''Lokavibhāga'' (literally "division of the universe") is a 5th-century Sanskrit text by Rishi Simhasuri. Its manuscript was first discovered in an Indian temple of Karnataka by M.R.R. Narasimhachar. The Lokavibhaga consists of 11 chapters ...
'', dated 458 CE, mentions the objectified numeral
meaning 'five voids, then two and seven, the sky, one and three and the form', i.e., the number 13107200000. Such objectified numbers were used extensively from the 6th century onward, especially after Varāhamihira
Varāhamihira ( 20/21 March 505 – 587), also called Varāha or Mihira, was an ancient Indian astrologer-astronomer who lived in or around Ujjain in present-day Madhya Pradesh, India.
Date
Unlike other prominent ancient Indian astronome ...
( 5th century CE). Zero is explicitly represented in such numbers as "the void" (''sunya'') or the "heaven-space" (''ambara akasha''). Correspondingly, the dot used in place of zero in written numerals was referred to as a ''sunya-bindu''.
Place-value numerals with zero
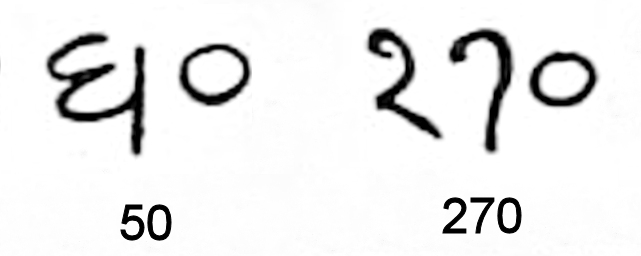 In 628 CE, astronomer-mathematician
In 628 CE, astronomer-mathematician Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
wrote his text '' Brahma Sphuta Siddhanta'' which contained the first mathematical treatment of zero. He defined zero as the result of subtracting a number from itself, postulated negative numbers and discussed their properties under arithmetical operations. His word for zero was ''shunya'' (void), the same term previously used for the empty spot in 9-digit place-value system. This provided a new perspective on the ''shunya-bindu'' as a numeral and paved the way for the eventual evolution of a zero digit. The dot continued to be used for at least 100 years afterwards, and transmitted to Southeast Asia and Arabia. Kashmir's Sharada script
The Śāradā, Sarada or Sharada script is an abugida writing system of the Brahmic family of scripts. The script was widespread between the 8th and 12th centuries in the northwestern parts of Indian Subcontinent (in Kashmir and neighbouring ...
has retained the dot for zero until this day.
By the end of the 7th century, decimal numbers begin to appear in inscriptions in Southeast Asia as well as in India.
Some scholars hold that they appeared even earlier. A 6th century copper-plate grant at Mankani bearing the numeral 346 (corresponding to 594 CE) is often cited. But its reliability is subject to dispute. The first indisputable occurrence of 0 in an inscription occurs at Gwalior
Gwalior (Hindi: , ) is a major city in the central Indian state of Madhya Pradesh; It is known as the Music City of India having oldest Gwalior gharana, musical gharana in existence. It is a major sports, cultural, industrial, and political c ...
in 876 CE, containing a numeral "270" in a notation surprisingly similar to the modern numerals. Throughout the 8th and 9th centuries, both the old Brahmi numerals and the new decimal numerals were used, sometimes appearing in the same inscriptions. In some documents, a transition is seen to occur around 866 CE.
Adoption by the Arabs
Before the rise of theCaliphate
A caliphate ( ) is an institution or public office under the leadership of an Islamic steward with Khalifa, the title of caliph (; , ), a person considered a political–religious successor to the Islamic prophet Muhammad and a leader of ...
, the Hindu–Arabic numeral system was already moving West and was mentioned in Syria
Syria, officially the Syrian Arab Republic, is a country in West Asia located in the Eastern Mediterranean and the Levant. It borders the Mediterranean Sea to the west, Turkey to Syria–Turkey border, the north, Iraq to Iraq–Syria border, t ...
in 662 AD by the Syriac Nestorian
Nestorianism is a term used in Christian theology and Church history to refer to several mutually related but doctrinarily distinct sets of teachings. The first meaning of the term is related to the original teachings of Christian theologian ...
scholar Severus Sebokht who wrote the following:
:''"I will omit all discussion of the science of the Indians, …, of their subtle discoveries in astronomy, discoveries that are more ingenious than those of the Greeks and the Babylonians, and of their valuable methods of calculation which surpass description. I wish only to say that this computation is done by means of nine signs. If those who believe, because they speak Greek, that they have arrived at the limits of science, would read the Indian texts, they would be convinced, even if a little late in the day, that there are others who know something of value."''
According to Al-Qifti
Jamāl al-Dīn Abū al-Ḥasan 'Alī ibn Yūsuf ibn Ibrāhīm ibn 'Abd al-Wahid al-Shaybānī (), called al-Qifṭī (; – 1248), was an Egyptian Arab historian, biographer, encyclopedist and administrator under the Ayyubid rulers of Aleppo ...
's ''History of Learned Men'':
:''"... a person from India presented himself before the Caliph al-Mansur in the year 76 ADwho was well versed in the siddhanta method of calculation related to the movement of the heavenly bodies, and having ways of calculating equations based on the half-chord ssentially the sinecalculated in half-degrees … This is all contained in a work … from which he claimed to have taken the half-chord calculated for one minute. Al-Mansur ordered this book to be translated into Arabic, and a work to be written, based on the translation, to give the Arab
Arabs (, , ; , , ) are an ethnic group mainly inhabiting the Arab world in West Asia and North Africa. A significant Arab diaspora is present in various parts of the world.
Arabs have been in the Fertile Crescent for thousands of years ...
s a solid base for calculating the movements of the planets …"''
The work was most likely to have been Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
's ''Brāhmasphuṭasiddhānta
The ''Brāhma-sphuṭa-siddhānta'' ("Correctly Established Doctrine of Brahma", abbreviated BSS)
is a main work of Brahmagupta, written c. 628. This text of mathematical astronomy contains significant mathematical content, including the first goo ...
'' (The Opening of the Universe) which was written in 628. Irrespective of whether this is wrong, since all Indian texts after Aryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was the first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy. His works include the '' Āryabhaṭīya'' (which mentions that in 3600 ' ...
's Aryabhatiya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Indian astronomy, Sanskrit astronomical treatise, is the ''Masterpiece, magnum opus'' and only known surviving work of the 5th century Indian mathematics, Indian mathematician Aryabhata. Philos ...
used the Indian number system, certainly from this time the Arabs had a translation of a text written in the Indian number system.
In his text ''The Arithmetic of Al-Uqlîdisî'' (Dordrecht: D. Reidel, 1978), A.S. Saidan's studies were unable to answer in full how the numerals reached the Arab world:
:''"It seems plausible that it drifted gradually, probably before the 7th century, through two channels, one starting from Sind, undergoing Persian filtration and spreading in what is now known as the Middle East, and the other starting from the coasts of the Indian Ocean
The Indian Ocean is the third-largest of the world's five oceanic divisions, covering or approximately 20% of the water area of Earth#Surface, Earth's surface. It is bounded by Asia to the north, Africa to the west and Australia (continent), ...
and extending to the southern coasts of the Mediterranean."''
Al-Uqlidisi developed a notation to represent decimal fractions. The numerals came to fame due to their use in the pivotal work of the Persian
Persian may refer to:
* People and things from Iran, historically called ''Persia'' in the English language
** Persians, the majority ethnic group in Iran, not to be conflated with the Iranic peoples
** Persian language, an Iranian language of the ...
mathematician Al-Khwarizmi
Muhammad ibn Musa al-Khwarizmi , or simply al-Khwarizmi, was a mathematician active during the Islamic Golden Age, who produced Arabic-language works in mathematics, astronomy, and geography. Around 820, he worked at the House of Wisdom in B ...
, whose book ''On the Calculation with Hindu Numerals'' was written about 825, and the Arab
Arabs (, , ; , , ) are an ethnic group mainly inhabiting the Arab world in West Asia and North Africa. A significant Arab diaspora is present in various parts of the world.
Arabs have been in the Fertile Crescent for thousands of years ...
mathematician Al-Kindi
Abū Yūsuf Yaʻqūb ibn ʼIsḥāq aṣ-Ṣabbāḥ al-Kindī (; ; ; ) was an Arab Muslim polymath active as a philosopher, mathematician, physician, and music theorist
Music theory is the study of theoretical frameworks for understandin ...
, who wrote four volumes (see "On the Use of the Indian Numerals" (Ketab fi Isti'mal al-'Adad al-Hindi) about 830. They, amongst other works, contributed to the diffusion of the Indian system of numeration in the Middle East
The Middle East (term originally coined in English language) is a geopolitical region encompassing the Arabian Peninsula, the Levant, Turkey, Egypt, Iran, and Iraq.
The term came into widespread usage by the United Kingdom and western Eur ...
and the West.
Development of symbols
The development of the numerals in early Europe is shown below:The abacus versus the Hindu–Arabic numeral system in early modern pictures
Adoption in Europe
*976. The first Arabic numerals in Europe appeared in the '' Codex Vigilanus'' in the year 976. *1202.Fibonacci
Leonardo Bonacci ( – ), commonly known as Fibonacci, was an Italians, Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages".
The name he is commonly called, ''Fibonacci ...
, an Italian
Italian(s) may refer to:
* Anything of, from, or related to the people of Italy over the centuries
** Italians, a Romance ethnic group related to or simply a citizen of the Italian Republic or Italian Kingdom
** Italian language, a Romance languag ...
mathematician who had studied in Béjaïa
Béjaïa ( ; , , ), formerly known as Bougie and Bugia, is a Mediterranean seaport, port city and communes of Algeria, commune on the Gulf of Béjaïa in Algeria; it is the capital of Béjaïa Province.
Geography
Location
Béjaïa owes its ...
(Bougie), Algeria, promoted the Arabic numeral system in Europe
Europe is a continent located entirely in the Northern Hemisphere and mostly in the Eastern Hemisphere. It is bordered by the Arctic Ocean to the north, the Atlantic Ocean to the west, the Mediterranean Sea to the south, and Asia to the east ...
with his book ''Liber Abaci
The or (Latin for "The Book of Calculation") was a 1202 Latin work on arithmetic by Leonardo of Pisa, posthumously known as Fibonacci. It is primarily famous for introducing both base-10 positional notation and the symbols known as Arabic n ...
'', which was published in 1202.
*1482. The system did not come into wide use in Europe, however, until the invention of printing
Printing is a process for mass reproducing text and images using a master form or template. The earliest non-paper products involving printing include cylinder seals and objects such as the Cyrus Cylinder and the Cylinders of Nabonidus. The ...
. (See, for example, th1482 Ptolemaeus map of the world
printed by Lienhart Holle in Ulm, and other examples in the Gutenberg Museum in
Mainz
Mainz (; #Names and etymology, see below) is the capital and largest city of the German state of Rhineland-Palatinate, and with around 223,000 inhabitants, it is List of cities in Germany by population, Germany's 35th-largest city. It lies in ...
, Germany
Germany, officially the Federal Republic of Germany, is a country in Central Europe. It lies between the Baltic Sea and the North Sea to the north and the Alps to the south. Its sixteen States of Germany, constituent states have a total popu ...
.)
*1512. The numerals appear in their modern form on the title page of ''Conpusicion de la arte de la arismetica y juntamente de geometría'' by Juan de Ortega.''Conpusicion de la arte de la arismetica y juntamente de geometría'', Juan de Ortega
*1549. The numerals appear in their modern form on the title page of ''Libro Intitulado Arithmetica Practica'' by Juan de Yciar, the Basque calligrapher and mathematician, published in Zaragoza
Zaragoza (), traditionally known in English as Saragossa ( ), is the capital city of the province of Zaragoza and of the autonomous communities of Spain, autonomous community of Aragon, Spain. It lies by the Ebro river and its tributaries, the ...
.
In the last few centuries, the European variety of Arabic numbers was spread around the world and gradually became the most commonly used numeral system in the world.
Even in many countries in languages which have their own numeral systems, the European Arabic numerals are widely used in commerce and mathematics.
Impact on arithmetic
The significance of the development of the positional number system is described by the French mathematicianPierre-Simon Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
(1749–1827) who wrote:
See also
* * *Notes
References
"The Development of Hindu–Arabic and Traditional Chinese Arithmetic" by Professor Lam Lay Yong, member of the International Academy of the History of Science
* {{DEFAULTSORT:History Of The Hindi-Arabic Numeral System Numeral systems Elementary mathematics Arabic language History of science and technology in India