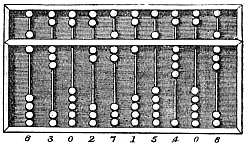
|
Place-value
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred (however, the value may be negated if placed before another digit). In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string. The Babylonian numeral system, base 60, was the first positional system to be developed, and its influence is present today ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today. History The prehistory of arithmetic is limited to a small number of artifacts, which may indicate the conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC, although its interpretation is disputed. The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations: addition, subtraction, multiplication, and division, as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, but t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonian Numerals
Assyro-Chaldean Babylonian cuneiform numerals were written in cuneiform (script), cuneiform, using a wedge-tipped Phragmites, reed stylus to make a mark on a soft clay tablet which would be exposed in the sun to harden to create a permanent record. The Babylonians, who were famous for their astronomical observations, as well as their calculations (aided by their invention of the abacus), used a sexagesimal (base-60) Positional notation, positional numeral system inherited from either the Sumerian or the Akkadian civilizations. Neither of the predecessors was a positional system (having a convention for which 'end' of the numeral represented the units). Origin This system first appeared around 2000 BC; its structure reflects the decimal lexical numerals of Semitic languages rather than Sumerian lexical numbers. However, the use of a special Sumerian sign for 60 (beside two Semitic signs for the same number) attests to a relation with the Sumerian system. Characters The Babyloni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero
0 (zero) is a number representing an empty quantity. In place-value notation Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the ... such as the Hindu–Arabic numeral system, 0 also serves as a placeholder numerical digit, which works by Multiplication, multiplying digits to the left of 0 by the radix, usually by 10. As a number, 0 fulfills a central role in mathematics as the additive identity of the integers, real numbers, and other algebraic structures. Common names for the number 0 in English are ''zero'', ''nought'', ''naught'' (), ''nil''. In contexts where at least one adjacent digit distinguishes it from the O, letter O, the number is sometimes pronounced as ''oh'' or ''o'' (). Informal or slang terms for 0 include ''zilch'' and ''zip''. Historically, ''ought'', ''aught'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numeral System
A numeral system (or system of numeration) is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using Numerical digit, digits or other symbols in a consistent manner. The same sequence of symbols may represent different numbers in different numeral systems. For example, "11" represents the number ''eleven'' in the decimal numeral system (used in common life), the number ''three'' in the binary numeral system (used in computers), and the number ''two'' in the unary numeral system (e.g. used in Tally marks, tallying scores). The number the numeral represents is called its value. Not all number systems can represent all numbers that are considered in the modern days; for example, Roman numerals have no zero. Ideally, a numeral system will: *Represent a useful set of numbers (e.g. all integers, or rational numbers) *Give every number represented a unique representation (or at least a standard representation) *Reflec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonian Numerals
Assyro-Chaldean Babylonian cuneiform numerals were written in cuneiform (script), cuneiform, using a wedge-tipped Phragmites, reed stylus to make a mark on a soft clay tablet which would be exposed in the sun to harden to create a permanent record. The Babylonians, who were famous for their astronomical observations, as well as their calculations (aided by their invention of the abacus), used a sexagesimal (base-60) Positional notation, positional numeral system inherited from either the Sumerian or the Akkadian civilizations. Neither of the predecessors was a positional system (having a convention for which 'end' of the numeral represented the units). Origin This system first appeared around 2000 BC; its structure reflects the decimal lexical numerals of Semitic languages rather than Sumerian lexical numbers. However, the use of a special Sumerian sign for 60 (beside two Semitic signs for the same number) attests to a relation with the Sumerian system. Characters The Babyloni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign-value Notation
A sign-value notation represents numbers by a series of numeric signs that added together equal the number represented. In Roman numerals for example, X means ten and L means fifty. Hence LXXX means eighty (50 + 10 + 10 + 10). There is no need for zero in sign-value notation. History Sign-value notation was the ancient way of writing numbers and only gradually evolved into place-value notation, also known as positional notation. When ancient people wanted to write "two sheep" in clay, they could inscribe in clay a picture of two sheep. But this would be impractical when they wanted to write "twenty sheep". In Mesopotamia they used small clay tokens to represent a number of a specific commodity, and strung the tokens like beads on a string, which were used for accounting. There was a token for one sheep and a token for ten sheep, and a different token for ten goats, etc. To ensure that nobody could alter the number and type of tokens, they invente ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positional Notation Glossary-en
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred (however, the value may be negated if placed before another digit). In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string. The Babylonian numeral system, base 60, was the first positional system to be developed, and its influence is present today ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roman Numerals
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written with combinations of letters from the Latin alphabet, each letter with a fixed integer value, modern style uses only these seven: The use of Roman numerals continued long after the decline of the Roman Empire. From the 14th century on, Roman numerals began to be replaced by Arabic numerals; however, this process was gradual, and the use of Roman numerals persists in some applications to this day. One place they are often seen is on clock faces. For instance, on the clock of Big Ben (designed in 1852), the hours from 1 to 12 are written as: The notations and can be read as "one less than five" (4) and "one less than ten" (9), although there is a tradition favouring representation of "4" as "" on Roman numeral clocks. Other common uses include year numbers on monuments and buildings and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hindu–Arabic Numeral System
The Hindu–Arabic numeral system or Indo-Arabic numeral system Audun HolmeGeometry: Our Cultural Heritage 2000 (also called the Hindu numeral system or Arabic numeral system) is a positional decimal numeral system, and is the most common system for the symbolic representation of numbers in the world. It was invented between the 1st and 4th centuries by Indian mathematicians. The system was adopted in Arabic mathematics by the 9th century. It became more widely known through the writings of the Persian mathematician Al-Khwārizmī: "Historians have speculated on al-Khwarizmi's native language. Since he was born in a former Persian province, he may have spoken the Persian language. It is also possible that he spoke Khwarezmian, a language of the region that is now extinct." (''On the Calculation with Hindu Numerals'', ) and Arab mathematician Al-Kindi (''On the Use of the Hindu Numerals'', ). The system had spread to medieval Europe by the High Middle Ages. The system is base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base-60
Sexagesimal, also known as base 60 or sexagenary, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form—for measuring time, angles, and geographic coordinates. The number 60, a superior highly composite number, has twelve factors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60, of which 2, 3, and 5 are prime numbers. With so many factors, many fractions involving sexagesimal numbers are simplified. For example, one hour can be divided evenly into sections of 30 minutes, 20 minutes, 15 minutes, 12 minutes, 10 minutes, 6 minutes, 5 minutes, 4 minutes, 3 minutes, 2 minutes, and 1 minute. 60 is the smallest number that is divisible by every number from 1 to 6; that is, it is the lowest common multiple of 1, 2, 3, 4, 5, and 6. ''In this article, all sexagesimal digits are represented as decimal numbers, except where otherwise noted. For ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counting Rods
Counting rods () are small bars, typically 3–14 cm long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number. The written forms based on them are called rod numerals. They are a true positional numeral system with digits for 1–9 and a blank for 0, from the Warring states period (circa 475 BCE) to the 16th century. History Chinese arithmeticians used counting rods well over two thousand years ago. In 1954 forty-odd counting rods of the Warring States period (5th century BCE to 221 BCE) were found in Zuǒjiāgōngshān (左家公山) Chu Grave No.15 in Changsha, Hunan. In 1973 archeologists unearthed a number of wood scripts from a tomb in Hubei dating from the period of the Han dynasty (206 BCE to 220 CE). On one of the wooden scripts was written: "当利二月定算𝍥". This is one of the earliest examples of using counting-rod numerals in writing. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
