Game theory is the study of
mathematical model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical m ...
s of strategic interactions.
It has applications in many fields of
social science
Social science (often rendered in the plural as the social sciences) is one of the branches of science, devoted to the study of societies and the relationships among members within those societies. The term was formerly used to refer to the ...
, and is used extensively in
economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
,
logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...
,
systems science and
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
. Initially, game theory addressed two-person
zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of
behavioral relations. It is now an
umbrella term
Hypernymy and hyponymy are the wikt:Wiktionary:Semantic relations, semantic relations between a generic term (''hypernym'') and a more specific term (''hyponym''). The hypernym is also called a ''supertype'', ''umbrella term'', or ''blanket term ...
for the
science
Science is a systematic discipline that builds and organises knowledge in the form of testable hypotheses and predictions about the universe. Modern science is typically divided into twoor threemajor branches: the natural sciences, which stu ...
of rational
decision making
In psychology, decision-making (also spelled decision making and decisionmaking) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several possible alternative options. It could be either ra ...
in humans, animals, and computers.
Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by
John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
. Von Neumann's original proof used the
Brouwer fixed-point theorem on continuous mappings into compact
convex set
In geometry, a set of points is convex if it contains every line segment between two points in the set.
For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is n ...
s, which became a standard method in game theory and
mathematical economics
Mathematical economics is the application of Mathematics, mathematical methods to represent theories and analyze problems in economics. Often, these Applied mathematics#Economics, applied methods are beyond simple geometry, and may include diff ...
. His paper was followed by ''
Theory of Games and Economic Behavior'' (1944), co-written with
Oskar Morgenstern
Oskar Morgenstern (; January 24, 1902 – July 26, 1977) was a German-born economist. In collaboration with mathematician John von Neumann, he is credited with founding the field of game theory and its application to social sciences and strategic ...
, which considered
cooperative games of several players. The second edition provided an
axiomatic theory of
expected utility
The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Ratio ...
, which allowed mathematical statisticians and economists to treat decision-making under uncertainty.
Game theory was developed extensively in the 1950s, and was explicitly applied to
evolution
Evolution is the change in the heritable Phenotypic trait, characteristics of biological populations over successive generations. It occurs when evolutionary processes such as natural selection and genetic drift act on genetic variation, re ...
in the 1970s, although similar developments go back at least as far as the 1930s. Game theory has been widely recognized as an important tool in many fields.
John Maynard Smith was awarded the
Crafoord Prize
The Crafoord Prize () is an annual science prize established in 1980 by Holger Crafoord, a Swedish industrialist, and his wife Anna-Greta Crafoord following a donation to the Royal Swedish Academy of Sciences. It is awarded jointly by the Acade ...
for his application of
evolutionary game theory in 1999, and fifteen game theorists have won the
Nobel Prize in economics as of 2020, including most recently
Paul Milgrom and
Robert B. Wilson.
History
Earliest results
In 1713, a letter attributed to Charles Waldegrave, an active
Jacobite and uncle to British diplomat
James Waldegrave, analyzed a game called "
le her". Waldegrave provided a
minimax mixed strategy solution to a two-person version of the card game, and the problem is now known as the
Waldegrave problem.
In 1838,
Antoine Augustin Cournot provided a
model of competition in
oligopolies. Though he did not refer to it as such, he presented a solution that is the
Nash equilibrium
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player could gain by changing their own strategy (holding all other players' strategies fixed) ...
of the game in his (''Researches into the Mathematical Principles of the Theory of Wealth''). In 1883,
Joseph Bertrand critiqued Cournot's model as unrealistic, providing an alternative model of price competition
which would later be formalized by
Francis Ysidro Edgeworth.
In 1913,
Ernst Zermelo published (''On an Application of Set Theory to the Theory of the Game of Chess''), which proved that the optimal chess strategy is
strictly determined.
Foundation

The work of
John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
established game theory as its own independent field in the early-to-mid 20th century, with von Neumann publishing his paper ''On the Theory of Games of Strategy'' in 1928. Von Neumann's original proof used
Brouwer's fixed-point theorem on continuous
mappings into compact
convex set
In geometry, a set of points is convex if it contains every line segment between two points in the set.
For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is n ...
s, which became a standard method in game theory and
mathematical economics
Mathematical economics is the application of Mathematics, mathematical methods to represent theories and analyze problems in economics. Often, these Applied mathematics#Economics, applied methods are beyond simple geometry, and may include diff ...
. Von Neumann's work in game theory culminated in his 1944 book ''
Theory of Games and Economic Behavior'', co-authored with
Oskar Morgenstern
Oskar Morgenstern (; January 24, 1902 – July 26, 1977) was a German-born economist. In collaboration with mathematician John von Neumann, he is credited with founding the field of game theory and its application to social sciences and strategic ...
. The second edition of this book provided an
axiomatic theory of utility, which reincarnated
Daniel Bernoulli's old theory of utility (of money) as an independent discipline. This foundational work contains the method for finding mutually consistent solutions for two-person zero-sum games. Subsequent work focused primarily on
cooperative game theory, which analyzes optimal strategies for groups of individuals, presuming that they can enforce agreements between them about proper strategies.
In his 1938 book and earlier notes,
Émile Borel
Félix Édouard Justin Émile Borel (; 7 January 1871 – 3 February 1956) was a French people, French mathematician and politician. As a mathematician, he was known for his founding work in the areas of measure theory and probability.
Biograp ...
proved a
minimax theorem for two-person zero-sum matrix games only when the pay-off matrix is symmetric and provided a solution to a non-trivial infinite game (known in English as
Blotto game). Borel conjectured the non-existence of mixed-strategy equilibria in
finite two-person zero-sum games, a conjecture that was proved false by von Neumann.

In 1950,
John Nash developed a criterion for mutual consistency of players' strategies known as the
Nash equilibrium
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player could gain by changing their own strategy (holding all other players' strategies fixed) ...
, applicable to a wider variety of games than the criterion proposed by von Neumann and Morgenstern. Nash proved that every finite n-player, non-zero-sum (not just two-player zero-sum)
non-cooperative game has what is now known as a Nash equilibrium in mixed strategies.
Game theory experienced a flurry of activity in the 1950s, during which the concepts of the
core, the
extensive form game,
fictitious play,
repeated games, and the
Shapley value were developed. The 1950s also saw the first applications of game theory to
philosophy
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, Value (ethics and social sciences), value, mind, and language. It is a rational an ...
and
political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and Power (social and political), power, and the analysis of political activities, political philosophy, political thought, polit ...
. The first mathematical discussion of the
prisoner's dilemma appeared, and an experiment was undertaken by mathematicians
Merrill M. Flood and
Melvin Dresher
Melvin Dresher (born Dreszer; March 13, 1911 – June 4, 1992) was a Poland, Polish-born United States, American mathematician, notable for developing, alongside Merrill M. Flood, Merrill Flood, the game theory, game theoretical model of cooperat ...
, as part of the
RAND Corporation
The RAND Corporation, doing business as RAND, is an American nonprofit global policy think tank, research institute, and public sector consulting firm. RAND engages in research and development (R&D) in several fields and industries. Since the ...
's investigations into game theory. RAND pursued the studies because of possible applications to global
nuclear strategy.
Prize-winning achievements
In 1965,
Reinhard Selten introduced his
solution concept of
subgame perfect equilibria, which further refined the Nash equilibrium. Later he would introduce
trembling hand perfection as well. In 1994 Nash, Selten and
Harsanyi became
Economics Nobel Laureates for their contributions to economic game theory.
In the 1970s, game theory was extensively applied in
biology
Biology is the scientific study of life and living organisms. It is a broad natural science that encompasses a wide range of fields and unifying principles that explain the structure, function, growth, History of life, origin, evolution, and ...
, largely as a result of the work of
John Maynard Smith and his
evolutionarily stable strategy. In addition, the concepts of
correlated equilibrium,
trembling hand perfection and
common knowledge were introduced and analyzed.
In 1994, John Nash was awarded the Nobel Memorial Prize in the Economic Sciences for his contribution to game theory. Nash's most famous contribution to game theory is the concept of the Nash equilibrium, which is a solution concept for
non-cooperative games, published in 1951. A Nash equilibrium is a set of strategies, one for each player, such that no player can improve their payoff by unilaterally changing their strategy.
In 2005, game theorists
Thomas Schelling and
Robert Aumann followed Nash, Selten, and Harsanyi as Nobel Laureates. Schelling worked on dynamic models, early examples of
evolutionary game theory. Aumann contributed more to the equilibrium school, introducing equilibrium coarsening and correlated equilibria, and developing an extensive formal analysis of the assumption of common knowledge and of its consequences.
In 2007,
Leonid Hurwicz,
Eric Maskin, and
Roger Myerson
Roger Bruce Myerson (born March 29, 1951) is an American economist and professor at the University of Chicago. He holds the title of the David L. Pearson Distinguished Service Professor of Global Conflict Studies at The Pearson Institute for the ...
were awarded the Nobel Prize in Economics "for having laid the foundations of
mechanism design theory". Myerson's contributions include the notion of
proper equilibrium, and an important graduate text: ''Game Theory, Analysis of Conflict''.
Hurwicz introduced and formalized the concept of
incentive compatibility.
In 2012,
Alvin E. Roth and
Lloyd S. Shapley were awarded the Nobel Prize in Economics "for the theory of stable allocations and the practice of market design". In 2014, the Nobel went to game theorist
Jean Tirole.
Different types of games
Cooperative / non-cooperative
A game is ''cooperative'' if the players are able to form binding commitments externally enforced (e.g. through
contract law
A contract is an agreement that specifies certain legally enforceable rights and obligations pertaining to two or more Party (law), parties. A contract typically involves consent to transfer of goods, Service (economics), services, money, or pr ...
). A game is ''non-cooperative'' if players cannot form alliances or if all agreements need to be
self-enforcing (e.g. through
credible threats).
Cooperative games are often analyzed through the framework of ''cooperative game theory'', which focuses on predicting which coalitions will form, the joint actions that groups take, and the resulting collective payoffs. It is different from ''non-cooperative game theory'' which focuses on predicting individual players' actions and payoffs by analyzing
Nash equilibria
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player could gain by changing their own strategy (holding all other players' strategies fixed) ...
.
Cooperative game theory provides a high-level approach as it describes only the structure and payoffs of coalitions, whereas non-cooperative game theory also looks at how strategic interaction will affect the distribution of payoffs. As non-cooperative game theory is more general, cooperative games can be analyzed through the approach of non-cooperative game theory (the converse does not hold) provided that sufficient assumptions are made to encompass all the possible strategies available to players due to the possibility of external enforcement of cooperation.
Symmetric / asymmetric
A symmetric game is a game where each player earns the same payoff when making the same choice. In other words, the identity of the player does not change the resulting game facing the other player. Many of the commonly studied 2×2 games are symmetric. The standard representations of
chicken
The chicken (''Gallus gallus domesticus'') is a domesticated subspecies of the red junglefowl (''Gallus gallus''), originally native to Southeast Asia. It was first domesticated around 8,000 years ago and is now one of the most common and w ...
, the prisoner's dilemma, and the
stag hunt are all symmetric games.
The most commonly studied asymmetric games are games where there are not identical strategy sets for both players. For instance, the
ultimatum game and similarly the
dictator game have different strategies for each player. It is possible, however, for a game to have identical strategies for both players, yet be asymmetric. For example, the game pictured in this section's graphic is asymmetric despite having identical strategy sets for both players.
Zero-sum / non-zero-sum
Zero-sum games (more generally, constant-sum games) are games in which choices by players can neither increase nor decrease the available resources. In zero-sum games, the total benefit goes to all players in a game, for every combination of strategies, and always adds to zero (more informally, a player benefits only at the equal expense of others).
Poker
Poker is a family of Card game#Comparing games, comparing card games in which Card player, players betting (poker), wager over which poker hand, hand is best according to that specific game's rules. It is played worldwide, with varying rules i ...
exemplifies a zero-sum game (ignoring the possibility of the house's cut), because one wins exactly the amount one's opponents lose. Other zero-sum games include
matching pennies and most classical board games including
Go and
chess
Chess is a board game for two players. It is an abstract strategy game that involves Perfect information, no hidden information and no elements of game of chance, chance. It is played on a square chessboard, board consisting of 64 squares arran ...
.
Many games studied by game theorists (including the famed prisoner's dilemma) are non-zero-sum games, because the
outcome has net results greater or less than zero. Informally, in non-zero-sum games, a gain by one player does not necessarily correspond with a loss by another.
Furthermore, ''constant-sum games'' correspond to activities like theft and gambling, but not to the fundamental economic situation in which there are potential
gains from trade
In economics, gains from trade are the net benefits to economic agents from being allowed an increase in voluntary trading with each other. In technical terms, they are the increase of consumer surplus plus producer surplus from lower tariffs ...
. It is possible to transform any constant-sum game into a (possibly asymmetric) zero-sum game by adding a dummy player (often called "the board") whose losses compensate the players' net winnings.
Simultaneous / sequential
Simultaneous games are games where both players move simultaneously, or instead the later players are unaware of the earlier players' actions (making them ''effectively'' simultaneous).
Sequential games (a type of dynamic games) are games where players do not make decisions simultaneously, and player's earlier actions affect the outcome and decisions of other players. This need not be
perfect information about every action of earlier players; it might be very little knowledge. For instance, a player may know that an earlier player did not perform one particular action, while they do not know which of the other available actions the first player actually performed.
The difference between simultaneous and sequential games is captured in the different representations discussed above. Often,
normal form is used to represent simultaneous games, while
extensive form is used to represent sequential ones. The transformation of extensive to normal form is one way, meaning that multiple extensive form games correspond to the same normal form. Consequently, notions of equilibrium for simultaneous games are insufficient for reasoning about sequential games; see
subgame perfection.
In short, the differences between sequential and simultaneous games are as follows:
Perfect information and imperfect information

An important subset of sequential games consists of games of perfect information. A game with perfect information means that all players, at every move in the game, know the previous history of the game and the moves previously made by all other players. An imperfect information game is played when the players do not know all moves already made by the opponent such as a simultaneous move game.
Examples of perfect-information games include
tic-tac-toe,
checkers
Checkers (American English), also known as draughts (; English in the Commonwealth of Nations, Commonwealth English), is a group of Abstract strategy game, strategy board games for two players which involve forward movements of uniform game ...
,
chess
Chess is a board game for two players. It is an abstract strategy game that involves Perfect information, no hidden information and no elements of game of chance, chance. It is played on a square chessboard, board consisting of 64 squares arran ...
, and
Go.
Many card games are games of imperfect information, such as
poker
Poker is a family of Card game#Comparing games, comparing card games in which Card player, players betting (poker), wager over which poker hand, hand is best according to that specific game's rules. It is played worldwide, with varying rules i ...
and
bridge
A bridge is a structure built to Span (engineering), span a physical obstacle (such as a body of water, valley, road, or railway) without blocking the path underneath. It is constructed for the purpose of providing passage over the obstacle, whi ...
. Perfect information is often confused with
complete information, which is a similar concept pertaining to the common knowledge of each player's sequence, strategies, and payoffs throughout gameplay. Complete information requires that every player know the strategies and payoffs available to the other players but not necessarily the actions taken, whereas perfect information is knowledge of all aspects of the game and players. Games of
incomplete information can be reduced, however, to games of imperfect information by introducing "
moves by nature".
Bayesian game
One of the assumptions of the Nash equilibrium is that every player has correct beliefs about the actions of the other players. However, there are many situations in game theory where participants do not fully understand the characteristics of their opponents. Negotiators may be unaware of their opponent's valuation of the object of negotiation, companies may be unaware of their opponent's cost functions, combatants may be unaware of their opponent's strengths, and jurors may be unaware of their colleague's interpretation of the evidence at trial. In some cases, participants may know the character of their opponent well, but may not know how well their opponent knows his or her own character.
Bayesian game means a strategic game with incomplete information. For a strategic game, decision makers are players, and every player has a group of actions. A core part of the imperfect information specification is the set of states. Every state completely describes a collection of characteristics relevant to the player such as their preferences and details about them. There must be a state for every set of features that some player believes may exist.
For example, where Player 1 is unsure whether Player 2 would rather date her or get away from her, while Player 2 understands Player 1's preferences as before. To be specific, supposing that Player 1 believes that Player 2 wants to date her under a probability of 1/2 and get away from her under a probability of 1/2 (this evaluation comes from Player 1's experience probably: she faces players who want to date her half of the time in such a case and players who want to avoid her half of the time). Due to the probability involved, the analysis of this situation requires to understand the player's preference for the draw, even though people are only interested in pure strategic equilibrium.
Combinatorial games
Games in which the difficulty of finding an optimal strategy stems from the multiplicity of possible moves are called combinatorial games. Examples include chess and
Go. Games that involve
imperfect information may also have a strong combinatorial character, for instance
backgammon
Backgammon is a two-player board game played with counters and dice on tables boards. It is the most widespread Western member of the large family of tables games, whose ancestors date back at least 1,600 years. The earliest record of backgammo ...
. There is no unified theory addressing combinatorial elements in games. There are, however, mathematical tools that can solve some particular problems and answer some general questions.
Games of perfect information have been studied in
combinatorial game theory, which has developed novel representations, e.g.
surreal numbers, as well as
combinatorial and
algebraic (and
sometimes non-constructive) proof methods to
solve games of certain types, including "loopy" games that may result in infinitely long sequences of moves. These methods address games with higher combinatorial complexity than those usually considered in traditional (or "economic") game theory. A typical game that has been solved this way is
Hex. A related field of study, drawing from
computational complexity theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem ...
, is
game complexity, which is concerned with estimating the computational difficulty of finding optimal strategies.
Research in
artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
has addressed both perfect and imperfect information games that have very complex combinatorial structures (like chess, go, or backgammon) for which no provable optimal strategies have been found. The practical solutions involve computational heuristics, like
alpha–beta pruning or use of
artificial neural network
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
s trained by
reinforcement learning
Reinforcement learning (RL) is an interdisciplinary area of machine learning and optimal control concerned with how an intelligent agent should take actions in a dynamic environment in order to maximize a reward signal. Reinforcement learnin ...
, which make games more tractable in computing practice.
Discrete and continuous games
Much of game theory is concerned with finite, discrete games that have a finite number of players, moves, events, outcomes, etc. Many concepts can be extended, however.
Continuous games allow players to choose a strategy from a continuous strategy set. For instance,
Cournot competition
Cournot competition is an economic model used to describe an industry structure in which companies compete on the amount of output they will produce, which they decide on independently of each other and at the same time. It is named after Antoine ...
is typically modeled with players' strategies being any non-negative quantities, including fractional quantities.
Differential games
Differential games such as the continuous
pursuit and evasion game are continuous games where the evolution of the players' state variables is governed by
differential equations. The problem of finding an optimal strategy in a differential game is closely related to the
optimal control theory. In particular, there are two types of strategies: the open-loop strategies are found using the
Pontryagin maximum principle while the closed-loop strategies are found using
Bellman's Dynamic Programming method.
A particular case of differential games are the games with a random
time horizon.
In such games, the terminal time is a random variable with a given
probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
function. Therefore, the players maximize the
mathematical expectation of the cost function. It was shown that the modified optimization problem can be reformulated as a discounted differential game over an infinite time interval.
Evolutionary game theory
Evolutionary game theory studies players who adjust their strategies over time according to rules that are not necessarily rational or farsighted.
In general, the evolution of strategies over time according to such rules is modeled as a
Markov chain
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally ...
with a state variable such as the current strategy profile or how the game has been played in the recent past. Such rules may feature imitation, optimization, or survival of the fittest.
In biology, such models can represent
evolution
Evolution is the change in the heritable Phenotypic trait, characteristics of biological populations over successive generations. It occurs when evolutionary processes such as natural selection and genetic drift act on genetic variation, re ...
, in which offspring adopt their parents' strategies and parents who play more successful strategies (i.e. corresponding to higher payoffs) have a greater number of offspring. In the social sciences, such models typically represent strategic adjustment by players who play a game many times within their lifetime and, consciously or unconsciously, occasionally adjust their strategies.
Stochastic outcomes (and relation to other fields)
Individual decision problems with stochastic outcomes are sometimes considered "one-player games". They may be modeled using similar tools within the related disciplines of
decision theory
Decision theory or the theory of rational choice is a branch of probability theory, probability, economics, and analytic philosophy that uses expected utility and probabilities, probability to model how individuals would behave Rationality, ratio ...
,
operations research
Operations research () (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a branch of applied mathematics that deals with the development and application of analytical methods to improve management and ...
, and areas of
artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
, particularly
AI planning (with uncertainty) and
multi-agent system. Although these fields may have different motivators, the mathematics involved are substantially the same, e.g. using
Markov decision processes (MDP).
Stochastic outcomes can also be modeled in terms of game theory by adding a randomly acting player who makes "chance moves" ("
moves by nature"). This player is not typically considered a third player in what is otherwise a two-player game, but merely serves to provide a roll of the dice where required by the game.
For some problems, different approaches to modeling stochastic outcomes may lead to different solutions. For example, the difference in approach between MDPs and the
minimax solution is that the latter considers the worst-case over a set of adversarial moves, rather than reasoning in expectation about these moves given a fixed probability distribution. The minimax approach may be advantageous where stochastic models of uncertainty are not available, but may also be overestimating extremely unlikely (but costly) events, dramatically swaying the strategy in such scenarios if it is assumed that an adversary can force such an event to happen.
(See
Black swan theory for more discussion on this kind of modeling issue, particularly as it relates to predicting and limiting losses in investment banking.)
General models that include all elements of stochastic outcomes, adversaries, and partial or noisy observability (of moves by other players) have also been studied. The "
gold standard
A gold standard is a backed currency, monetary system in which the standard economics, economic unit of account is based on a fixed quantity of gold. The gold standard was the basis for the international monetary system from the 1870s to the ...
" is considered to be partially observable
stochastic game (POSG), but few realistic problems are computationally feasible in POSG representation.
Metagames
These are games the play of which is the development of the rules for another game, the target or subject game.
Metagame
A metagame, broadly defined as "a game beyond the game", typically refers to either of two concepts: a game which revolves around a core game; or the strategies and approaches to playing a game. A metagame can serve a broad range of purposes, a ...
s seek to maximize the utility value of the rule set developed. The theory of metagames is related to
mechanism design theory.
The term
metagame analysis is also used to refer to a practical approach developed by Nigel Howard, whereby a situation is framed as a strategic game in which stakeholders try to realize their objectives by means of the options available to them. Subsequent developments have led to the formulation of
confrontation analysis.
Mean field game theory
Mean field game theory is the study of strategic decision making in very large populations of small interacting agents. This class of problems was considered in the economics literature by
Boyan Jovanovic and
Robert W. Rosenthal, in the engineering literature by
Peter E. Caines, and by mathematicians
Pierre-Louis Lions and Jean-Michel Lasry.
Representation of games
The games studied in game theory are well-defined mathematical objects. To be fully defined, a game must specify the following elements: the ''players'' of the game, the ''information'' and ''actions'' available to each player at each decision point, and the
''payoffs'' for each outcome. (Eric Rasmusen refers to these four "essential elements" by the acronym "PAPI".)
A game theorist typically uses these elements, along with a
solution concept of their choosing, to deduce a set of equilibrium
strategies for each player such that, when these strategies are employed, no player can profit by unilaterally deviating from their strategy. These equilibrium strategies determine an
equilibrium to the game—a stable state in which either one outcome occurs or a set of outcomes occur with known probability.
Most cooperative games are presented in the characteristic function form, while the extensive and the normal forms are used to define noncooperative games.
Extensive form

The extensive form can be used to formalize games with a time sequencing of moves. Extensive form games can be visualized using game
trees (as pictured here). Here each
vertex (or node) represents a point of choice for a player. The player is specified by a number listed by the vertex. The lines out of the vertex represent a possible action for that player. The payoffs are specified at the bottom of the tree. The extensive form can be viewed as a multi-player generalization of a
decision tree
A decision tree is a decision support system, decision support recursive partitioning structure that uses a Tree (graph theory), tree-like Causal model, model of decisions and their possible consequences, including probability, chance event ou ...
. To solve any extensive form game,
backward induction must be used. It involves working backward up the game tree to determine what a rational player would do at the last vertex of the tree, what the player with the previous move would do given that the player with the last move is rational, and so on until the first vertex of the tree is reached.
The game pictured consists of two players. The way this particular game is structured (i.e., with sequential decision making and perfect information), ''Player 1'' "moves" first by choosing either or (fair or unfair). Next in the sequence, ''Player 2'', who has now observed ''Player 1''s move, can choose to play either or (accept or reject). Once ''Player 2'' has made their choice, the game is considered finished and each player gets their respective payoff, represented in the image as two numbers, where the first number represents Player 1's payoff, and the second number represents Player 2's payoff. Suppose that ''Player 1'' chooses and then ''Player 2'' chooses : ''Player 1'' then gets a payoff of "eight" (which in real-world terms can be interpreted in many ways, the simplest of which is in terms of money but could mean things such as eight days of vacation or eight countries conquered or even eight more opportunities to play the same game against other players) and ''Player 2'' gets a payoff of "two".
The extensive form can also capture simultaneous-move games and games with imperfect information. To represent it, either a dotted line connects different vertices to represent them as being part of the same information set (i.e. the players do not know at which point they are), or a closed line is drawn around them. (See example in the
imperfect information section.)
Normal form
The normal (or strategic form) game is usually represented by a
matrix which shows the players, strategies, and payoffs (see the example to the right). More generally it can be represented by any function that associates a payoff for each player with every possible combination of actions. In the accompanying example there are two players; one chooses the row and the other chooses the column. Each player has two strategies, which are specified by the number of rows and the number of columns. The payoffs are provided in the interior. The first number is the payoff received by the row player (Player 1 in our example); the second is the payoff for the column player (Player 2 in our example). Suppose that Player 1 plays ''Up'' and that Player 2 plays ''Left''. Then Player 1 gets a payoff of 4, and Player 2 gets 3.
When a game is presented in normal form, it is presumed that each player acts simultaneously or, at least, without knowing the actions of the other. If players have some information about the choices of other players, the game is usually presented in extensive form.
Every extensive-form game has an equivalent normal-form game, however, the transformation to normal form may result in an exponential blowup in the size of the representation, making it computationally impractical.
Characteristic function form
In cooperative game theory the characteristic function lists the payoff of each coalition. The origin of this formulation is in John von Neumann and Oskar Morgenstern's book.
Formally, a characteristic function is a function
from the set of all possible coalitions of players to a set of payments, and also satisfies
. The function describes how much collective payoff a set of players can gain by forming a coalition.
Alternative game representations
Alternative game representation forms are used for some subclasses of games or adjusted to the needs of interdisciplinary research. In addition to classical game representations, some of the alternative representations also encode time related aspects.
General and applied uses
As a method of
applied mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a ...
, game theory has been used to study a wide variety of human and animal behaviors. It was initially developed in
economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
to understand a large collection of economic behaviors, including behaviors of firms, markets, and consumers. The first use of game-theoretic analysis was by
Antoine Augustin Cournot in 1838 with his solution of the
Cournot duopoly
Cournot competition is an economic model used to describe an industry structure in which companies compete on the amount of output they will produce, which they decide on independently of each other and at the same time. It is named after Antoine A ...
. The use of game theory in the social sciences has expanded, and game theory has been applied to political, sociological, and psychological behaviors as well.
Although pre-twentieth-century
naturalists such as
Charles Darwin
Charles Robert Darwin ( ; 12 February 1809 – 19 April 1882) was an English Natural history#Before 1900, naturalist, geologist, and biologist, widely known for his contributions to evolutionary biology. His proposition that all speci ...
made game-theoretic kinds of statements, the use of game-theoretic analysis in biology began with
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who a ...
's studies of animal behavior during the 1930s. This work predates the name "game theory", but it shares many important features with this field. The developments in economics were later applied to biology largely by John Maynard Smith in his 1982 book ''
Evolution and the Theory of Games''.
In addition to being used to describe, predict, and explain behavior, game theory has also been used to develop theories of ethical or normative behavior and to
prescribe such behavior.
In
economics and philosophy, scholars have applied game theory to help in the understanding of good or proper behavior. Game-theoretic approaches have also been suggested in the
philosophy of language
Philosophy of language refers to the philosophical study of the nature of language. It investigates the relationship between language, language users, and the world. Investigations may include inquiry into the nature of Meaning (philosophy), me ...
and
philosophy of science
Philosophy of science is the branch of philosophy concerned with the foundations, methods, and implications of science. Amongst its central questions are the difference between science and non-science, the reliability of scientific theories, ...
. Game-theoretic arguments of this type can be found as far back as
Plato
Plato ( ; Greek language, Greek: , ; born BC, died 348/347 BC) was an ancient Greek philosopher of the Classical Greece, Classical period who is considered a foundational thinker in Western philosophy and an innovator of the writte ...
. An alternative version of game theory, called chemical game theory, represents the player's choices as metaphorical chemical reactant molecules called "knowlecules". Chemical game theory then calculates the outcomes as equilibrium solutions to a system of chemical reactions.
Description and modeling

The primary use of game theory is to describe and
model
A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , .
Models can be divided in ...
how human populations behave. Some scholars believe that by finding the equilibria of games they can predict how actual human populations will behave when confronted with situations analogous to the game being studied. This particular view of game theory has been criticized. It is argued that the assumptions made by game theorists are often violated when applied to real-world situations. Game theorists usually assume players act rationally, but in practice, human rationality and/or behavior often deviates from the model of rationality as used in game theory. Game theorists respond by comparing their assumptions to those used in
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
. Thus while their assumptions do not always hold, they can treat game theory as a reasonable scientific
ideal akin to the models used by
physicist
A physicist is a scientist who specializes in the field of physics, which encompasses the interactions of matter and energy at all length and time scales in the physical universe. Physicists generally are interested in the root or ultimate cau ...
s. However, empirical work has shown that in some classic games, such as the
centipede game,
guess 2/3 of the average game, and the
dictator game, people regularly do not play Nash equilibria. There is an ongoing debate regarding the importance of these experiments and whether the analysis of the experiments fully captures all aspects of the relevant situation.
Some game theorists, following the work of John Maynard Smith and
George R. Price, have turned to evolutionary game theory in order to resolve these issues. These models presume either no rationality or
bounded rationality
Bounded rationality is the idea that rationality is limited when individuals decision-making, make decisions, and under these limitations, rational individuals will select a decision that is satisficing, satisfactory rather than optimal.
Limitat ...
on the part of players. Despite the name, evolutionary game theory does not necessarily presume
natural selection
Natural selection is the differential survival and reproduction of individuals due to differences in phenotype. It is a key mechanism of evolution, the change in the Heredity, heritable traits characteristic of a population over generation ...
in the biological sense. Evolutionary game theory includes both biological as well as cultural evolution and also models of individual learning (for example,
fictitious play dynamics).
Prescriptive or normative analysis
Some scholars see game theory not as a predictive tool for the behavior of human beings, but as a suggestion for how people ought to behave. Since a strategy, corresponding to a Nash equilibrium of a game constitutes one's
best response to the actions of the other players – provided they are in (the same) Nash equilibrium – playing a strategy that is part of a Nash equilibrium seems appropriate. This normative use of game theory has also come under criticism.
Economics
Game theory is a major method used in mathematical economics and business for
modeling competing behaviors of interacting
agents. Applications include a wide array of economic phenomena and approaches, such as
auctions,
bargaining
In the social sciences, bargaining or haggling is a type of negotiation in which the buyer and seller of a Goods and services, good or service debate the price or nature of a Financial transaction, transaction. If the bargaining produces agree ...
,
mergers and acquisitions
Mergers and acquisitions (M&A) are business transactions in which the ownership of a company, business organization, or one of their operating units is transferred to or consolidated with another entity. They may happen through direct absorpt ...
pricing,
fair division
Fair division is the problem in game theory of dividing a set of resources among several people who have an Entitlement (fair division), entitlement to them so that each person receives their due share. The central tenet of fair division is that ...
,
duopolies,
oligopolies,
social network
A social network is a social structure consisting of a set of social actors (such as individuals or organizations), networks of Dyad (sociology), dyadic ties, and other Social relation, social interactions between actors. The social network per ...
formation,
agent-based computational economics,
general equilibrium, mechanism design,
and
voting system
An electoral or voting system is a set of rules used to determine the results of an election. Electoral systems are used in politics to elect governments, while non-political elections may take place in business, nonprofit organizations and inf ...
s; and across such broad areas as experimental economics,
behavioral economics
Behavioral economics is the study of the psychological (e.g. cognitive, behavioral, affective, social) factors involved in the decisions of individuals or institutions, and how these decisions deviate from those implied by traditional economi ...
,
information economics,
industrial organization
In economics, industrial organization is a field that builds on the theory of the firm by examining the structure of (and, therefore, the boundaries between) firms and markets. Industrial organization adds real-world complications to the per ...
, and
political economy
Political or comparative economy is a branch of political science and economics studying economic systems (e.g. Marketplace, markets and national economies) and their governance by political systems (e.g. law, institutions, and government). Wi ...
.
This research usually focuses on particular sets of strategies known as
"solution concepts" or "equilibria". A common assumption is that players act rationally. In non-cooperative games, the most famous of these is the Nash equilibrium. A set of strategies is a Nash equilibrium if each represents a best response to the other strategies. If all the players are playing the strategies in a Nash equilibrium, they have no unilateral incentive to deviate, since their strategy is the best they can do given what others are doing.
The payoffs of the game are generally taken to represent the
utility
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings.
* In a normative context, utility refers to a goal or objective that we wish ...
of individual players.
A prototypical paper on game theory in economics begins by presenting a game that is an abstraction of a particular economic situation. One or more solution concepts are chosen, and the author demonstrates which strategy sets in the presented game are equilibria of the appropriate type. Economists and business professors suggest two primary uses (noted above): ''descriptive'' and ''
prescriptive''.
Managerial economics
Game theory also has an extensive use in a specific branch or stream of economics –
Managerial Economics
Managerial economics is a branch of economics involving the application of economic methods in the organizational decision-making process.*
*
* Economics is the study of the production, distribution, and consumption of goods and services. Manag ...
. One important usage of it in the field of managerial economics is in analyzing strategic interactions between firms. For example, firms may be competing in a market with limited resources, and game theory can help managers understand how their decisions impact their competitors and the overall market outcomes. Game theory can also be used to analyze cooperation between firms, such as in forming strategic alliances or joint ventures. Another use of game theory in managerial economics is in analyzing pricing strategies. For example, firms may use game theory to determine the optimal
pricing strategy based on how they expect their competitors to respond to their pricing decisions. Overall, game theory serves as a useful tool for analyzing strategic interactions and decision making in the context of managerial economics.
Business
The
Chartered Institute of Procurement & Supply (CIPS) promotes knowledge and use of game theory within the context of business
procurement
Procurement is the process of locating and agreeing to terms and purchasing goods, services, or other works from an external source, often with the use of a tendering or competitive bidding process. The term may also refer to a contractual ...
. CIPS and TWS Partners have conducted a series of surveys designed to explore the understanding, awareness and application of game theory among
procurement
Procurement is the process of locating and agreeing to terms and purchasing goods, services, or other works from an external source, often with the use of a tendering or competitive bidding process. The term may also refer to a contractual ...
professionals. Some of the main findings in their third annual survey (2019) include:
*application of game theory to procurement activity has increased – at the time it was at 19% across all survey respondents
*65% of participants predict that use of game theory applications will grow
*70% of respondents say that they have "only a basic or a below basic understanding" of game theory
*20% of participants had undertaken
on-the-job training in game theory
*50% of respondents said that new or improved software solutions were desirable
*90% of respondents said that they do not have the software they need for their work.
Project management
Sensible decision-making is critical for the success of projects. In project management, game theory is used to model the decision-making process of players, such as investors, project managers, contractors, sub-contractors, governments and customers. Quite often, these players have competing interests, and sometimes their interests are directly detrimental to other players, making project management scenarios well-suited to be modeled by game theory.
Piraveenan (2019)
in his review provides several examples where game theory is used to model project management scenarios. For instance, an investor typically has several investment options, and each option will likely result in a different project, and thus one of the investment options has to be chosen before the project charter can be produced. Similarly, any large project involving subcontractors, for instance, a construction project, has a complex interplay between the main contractor (the project manager) and subcontractors, or among the subcontractors themselves, which typically has several decision points. For example, if there is an ambiguity in the contract between the contractor and subcontractor, each must decide how hard to push their case without jeopardizing the whole project, and thus their own stake in it. Similarly, when projects from competing organizations are launched, the marketing personnel have to decide what is the best timing and strategy to market the project, or its resultant product or service, so that it can gain maximum traction in the face of competition. In each of these scenarios, the required decisions depend on the decisions of other players who, in some way, have competing interests to the interests of the decision-maker, and thus can ideally be modeled using game theory.
Piraveenan
summarizes that two-player games are predominantly used to model project management scenarios, and based on the identity of these players, five distinct types of games are used in project management.
* Government-sector–private-sector games (games that model
public–private partnerships)
* Contractor–contractor games
* Contractor–subcontractor games
* Subcontractor–subcontractor games
* Games involving other players
In terms of types of games, both cooperative as well as non-cooperative, normal-form as well as extensive-form, and zero-sum as well as non-zero-sum are used to model various project management scenarios.
Political science
The application of game theory to
political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and Power (social and political), power, and the analysis of political activities, political philosophy, political thought, polit ...
is focused in the overlapping areas of
fair division
Fair division is the problem in game theory of dividing a set of resources among several people who have an Entitlement (fair division), entitlement to them so that each person receives their due share. The central tenet of fair division is that ...
,
political economy
Political or comparative economy is a branch of political science and economics studying economic systems (e.g. Marketplace, markets and national economies) and their governance by political systems (e.g. law, institutions, and government). Wi ...
,
public choice,
war bargaining,
positive political theory, and
social choice theory
Social choice theory is a branch of welfare economics that extends the Decision theory, theory of rational choice to collective decision-making. Social choice studies the behavior of different mathematical procedures (social welfare function, soc ...
. In each of these areas, researchers have developed game-theoretic models in which the players are often voters, states, special interest groups, and politicians.
Early examples of game theory applied to political science are provided by
Anthony Downs. In his 1957 book ''
An Economic Theory of Democracy'', he applies the
Hotelling firm location model to the political process. In the Downsian model, political candidates commit to ideologies on a one-dimensional policy space. Downs first shows how the political candidates will converge to the ideology preferred by the median voter if voters are fully informed, but then argues that voters choose to remain rationally ignorant which allows for candidate divergence. Game theory was applied in 1962 to the
Cuban Missile Crisis
The Cuban Missile Crisis, also known as the October Crisis () in Cuba, or the Caribbean Crisis (), was a 13-day confrontation between the governments of the United States and the Soviet Union, when American deployments of Nuclear weapons d ...
during the presidency of John F. Kennedy.
It has also been proposed that game theory explains the stability of any form of political government. Taking the simplest case of a monarchy, for example, the king, being only one person, does not and cannot maintain his authority by personally exercising physical control over all or even any significant number of his subjects. Sovereign control is instead explained by the recognition by each citizen that all other citizens expect each other to view the king (or other established government) as the person whose orders will be followed. Coordinating communication among citizens to replace the sovereign is effectively barred, since conspiracy to replace the sovereign is generally punishable as a crime. Thus, in a process that can be modeled by variants of the prisoner's dilemma, during periods of stability no citizen will find it rational to move to replace the sovereign, even if all the citizens know they would be better off if they were all to act collectively.
A game-theoretic explanation for
democratic peace is that public and open debate in democracies sends clear and reliable information regarding their intentions to other states. In contrast, it is difficult to know the intentions of nondemocratic leaders, what effect concessions will have, and if promises will be kept. Thus there will be mistrust and unwillingness to make concessions if at least one of the parties in a dispute is a non-democracy.
However, game theory predicts that two countries may still go to war even if their leaders are cognizant of the costs of fighting. War may result from asymmetric information; two countries may have incentives to mis-represent the amount of military resources they have on hand, rendering them unable to settle disputes agreeably without resorting to fighting. Moreover, war may arise because of commitment problems: if two countries wish to settle a dispute via peaceful means, but each wishes to go back on the terms of that settlement, they may have no choice but to resort to warfare. Finally, war may result from issue indivisibilities.
Game theory could also help predict a nation's responses when there is a new rule or law to be applied to that nation. One example is Peter John Wood's (2013) research looking into what nations could do to help reduce climate change. Wood thought this could be accomplished by making treaties with other nations to reduce
greenhouse gas emissions
Greenhouse gas (GHG) emissions from human activities intensify the greenhouse effect. This contributes to climate change. Carbon dioxide (), from burning fossil fuels such as coal, petroleum, oil, and natural gas, is the main cause of climate chan ...
. However, he concluded that this idea could not work because it would create a prisoner's dilemma for the nations.
Defence science and technology
Game theory has been used extensively to model decision-making scenarios relevant to defence applications.
Most studies that has applied game theory in defence settings are concerned with Command and Control Warfare, and can be further classified into studies dealing with (i) Resource Allocation Warfare (ii) Information Warfare (iii) Weapons Control Warfare, and (iv) Adversary Monitoring Warfare.
Many of the problems studied are concerned with sensing and tracking, for example a surface ship trying to track a hostile submarine and the submarine trying to evade being tracked, and the interdependent decision making that takes place with regards to bearing, speed, and the sensor technology activated by both vessels.
The tool,
for example, automates the transformation of public vulnerability data into models, allowing defenders to synthesize optimal defence strategies through Stackelberg equilibrium analysis. This approach enhances cyber resilience by enabling defenders to anticipate and counteract attackers’ best responses, making game theory increasingly relevant in adversarial cybersecurity environments.
Ho et al. provide a broad summary of game theory applications in defence, highlighting its advantages and limitations across both physical and cyber domains.
Biology
Unlike those in economics, the payoffs for games in
biology
Biology is the scientific study of life and living organisms. It is a broad natural science that encompasses a wide range of fields and unifying principles that explain the structure, function, growth, History of life, origin, evolution, and ...
are often interpreted as corresponding to
fitness. In addition, the focus has been less on equilibria that correspond to a notion of rationality and more on ones that would be maintained by evolutionary forces. The best-known equilibrium in biology is known as the ''
evolutionarily stable strategy'' (ESS), first introduced in . Although its initial motivation did not involve any of the mental requirements of the Nash equilibrium, every ESS is a Nash equilibrium.
In biology, game theory has been used as a model to understand many different phenomena. It was first used to explain the evolution (and stability) of the approximate 1:1
sex ratio
A sex ratio is the ratio of males to females in a population. As explained by Fisher's principle, for evolutionary reasons this is typically about 1:1 in species which reproduce sexually. However, many species deviate from an even sex ratio, ei ...
s. suggested that the 1:1 sex ratios are a result of evolutionary forces acting on individuals who could be seen as trying to maximize their number of grandchildren.
Additionally, biologists have used evolutionary game theory and the ESS to explain the emergence of
animal communication
Animal communication is the transfer of information from one or a group of animals (sender or senders) to one or more other animals (receiver or receivers) that affects the current or future behavior of the receivers. Information may be sent int ...
. The analysis of
signaling games and
other communication games has provided insight into the evolution of communication among animals. For example, the
mobbing behavior of many species, in which a large number of prey animals attack a larger predator, seems to be an example of spontaneous emergent organization. Ants have also been shown to exhibit feed-forward behavior akin to fashion (see
Paul Ormerod's ''
Butterfly Economics'').
Biologists have used the
game of chicken to analyze fighting behavior and territoriality.
According to Maynard Smith, in the preface to ''Evolution and the Theory of Games'', "paradoxically, it has turned out that game theory is more readily applied to biology than to the field of economic behaviour for which it was originally designed". Evolutionary game theory has been used to explain many seemingly incongruous phenomena in nature.
One such phenomenon is known as
biological altruism. This is a situation in which an organism appears to act in a way that benefits other organisms and is detrimental to itself. This is distinct from traditional notions of altruism because such actions are not conscious, but appear to be evolutionary adaptations to increase overall fitness. Examples can be found in species ranging from vampire bats that regurgitate blood they have obtained from a night's hunting and give it to group members who have failed to feed, to worker bees that care for the queen bee for their entire lives and never mate, to
vervet monkeys that warn group members of a predator's approach, even when it endangers that individual's chance of survival.
All of these actions increase the overall fitness of a group, but occur at a cost to the individual.
Evolutionary game theory explains this altruism with the idea of
kin selection
Kin selection is a process whereby natural selection favours a trait due to its positive effects on the reproductive success of an organism's relatives, even when at a cost to the organism's own survival and reproduction. Kin selection can lead ...
. Altruists discriminate between the individuals they help and favor relatives.
Hamilton's rule explains the evolutionary rationale behind this selection with the equation , where the cost to the altruist must be less than the benefit to the recipient multiplied by the coefficient of relatedness . The more closely related two organisms are causes the incidences of altruism to increase because they share many of the same alleles. This means that the altruistic individual, by ensuring that the alleles of its close relative are passed on through survival of its offspring, can forgo the option of having offspring itself because the same number of alleles are passed on. For example, helping a sibling (in diploid animals) has a coefficient of , because (on average) an individual shares half of the alleles in its sibling's offspring. Ensuring that enough of a sibling's offspring survive to adulthood precludes the necessity of the altruistic individual producing offspring.
The coefficient values depend heavily on the scope of the playing field; for example if the choice of whom to favor includes all genetic living things, not just all relatives, we assume the discrepancy between all humans only accounts for approximately 1% of the diversity in the playing field, a coefficient that was in the smaller field becomes 0.995. Similarly if it is considered that information other than that of a genetic nature (e.g. epigenetics, religion, science, etc.) persisted through time the playing field becomes larger still, and the discrepancies smaller.
Computer science and logic
Game theory has come to play an increasingly important role in
logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...
and in
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
. Several logical theories have a basis in
game semantics. In addition, computer scientists have used games to model
interactive computations. Also, game theory provides a theoretical basis to the field of
multi-agent systems.
Separately, game theory has played a role in
online algorithms; in particular, the
-server problem, which has in the past been referred to as ''games with moving costs'' and ''request-answer games''.
Yao's principle is a game-theoretic technique for proving
lower bounds on the
computational complexity of
randomized algorithms, especially online algorithms.
The emergence of the Internet has motivated the development of algorithms for finding equilibria in games, markets, computational auctions, peer-to-peer systems, and security and information markets.
Algorithmic game theory and within it
algorithmic mechanism design combine computational
algorithm design and analysis of
complex system
A complex system is a system composed of many components that may interact with one another. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication sy ...
s with economic theory.
Game theory has multiple applications in the field of artificial intelligence and machine learning. It is often used in developing autonomous systems that can make complex decisions in uncertain environment. Some other areas of application of game theory in AI/ML context are as follows - multi-agent system formation, reinforcement learning, mechanism design etc. By using game theory to model the behavior of other agents and anticipate their actions, AI/ML systems can make better decisions and operate more effectively.
Philosophy
Game theory has been put to several uses in
philosophy
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, Value (ethics and social sciences), value, mind, and language. It is a rational an ...
. Responding to two papers by , used game theory to develop a philosophical account of
convention. In so doing, he provided the first analysis of
common knowledge and employed it in analyzing play in
coordination games. In addition, he first suggested that one can understand
meaning in terms of
signaling games. This later suggestion has been pursued by several philosophers since Lewis. Following game-theoretic account of conventions, Edna Ullmann-Margalit (1977) and
Bicchieri (2006) have developed theories of
social norms that define them as Nash equilibria that result from transforming a mixed-motive game into a coordination game.
Game theory has also challenged philosophers to think in terms of interactive
epistemology
Epistemology is the branch of philosophy that examines the nature, origin, and limits of knowledge. Also called "the theory of knowledge", it explores different types of knowledge, such as propositional knowledge about facts, practical knowle ...
: what it means for a collective to have common beliefs or knowledge, and what are the consequences of this knowledge for the social outcomes resulting from the interactions of agents. Philosophers who have worked in this area include Bicchieri (1989, 1993),
Skyrms (1990), and
Stalnaker (1999).
The synthesis of game theory with
ethics
Ethics is the philosophy, philosophical study of Morality, moral phenomena. Also called moral philosophy, it investigates Normativity, normative questions about what people ought to do or which behavior is morally right. Its main branches inclu ...
was championed by
R. B. Braithwaite. The hope was that rigorous mathematical analysis of game theory might help formalize the more imprecise philosophical discussions. However, this expectation was only materialized to a limited extent.
In
ethics
Ethics is the philosophy, philosophical study of Morality, moral phenomena. Also called moral philosophy, it investigates Normativity, normative questions about what people ought to do or which behavior is morally right. Its main branches inclu ...
, some (most notably David Gauthier, Gregory Kavka, and Jean Hampton) authors have attempted to pursue
Thomas Hobbes
Thomas Hobbes ( ; 5 April 1588 – 4 December 1679) was an English philosopher, best known for his 1651 book ''Leviathan (Hobbes book), Leviathan'', in which he expounds an influential formulation of social contract theory. He is considered t ...
' project of deriving morality from self-interest. Since games like the
prisoner's dilemma present an apparent conflict between morality and self-interest, explaining why cooperation is required by self-interest is an important component of this project. This general strategy is a component of the general
social contract
In moral and political philosophy, the social contract is an idea, theory, or model that usually, although not always, concerns the legitimacy of the authority of the state over the individual. Conceptualized in the Age of Enlightenment, it ...
view in
political philosophy
Political philosophy studies the theoretical and conceptual foundations of politics. It examines the nature, scope, and Political legitimacy, legitimacy of political institutions, such as State (polity), states. This field investigates different ...
(for examples, see and ).
Other authors have attempted to use evolutionary game theory in order to explain the emergence of human attitudes about morality and corresponding animal behaviors. These authors look at several games including the prisoner's dilemma,
stag hunt, and the
Nash bargaining game as providing an explanation for the emergence of attitudes about morality (see, e.g., and ).
Epidemiology
Since the decision to take a vaccine for a particular disease is often made by individuals, who may consider a range of factors and parameters in making this decision (such as the incidence and prevalence of the disease, perceived and real risks associated with contracting the disease, mortality rate, perceived and real risks associated with vaccination, and financial cost of vaccination), game theory has been used to model and predict vaccination uptake in a society.
Well known examples of games
Prisoner's dilemma
William Poundstone described the game in his 1993 book Prisoner's Dilemma:
Two members of a criminal gang, A and B, are arrested and imprisoned. Each prisoner is in solitary confinement with no means of communication with their partner. The principal charge would lead to a sentence of ten years in prison; however, the police do not have the evidence for a conviction. They plan to sentence both to two years in prison on a lesser charge but offer each prisoner a Faustian bargain: If one of them confesses to the crime of the principal charge, betraying the other, they will be pardoned and free to leave while the other must serve the entirety of the sentence instead of just two years for the lesser charge.
The
dominant strategy (and therefore the best response to any possible opponent strategy), is to betray the other, which aligns with the
sure-thing principle. However, both prisoners staying silent would yield a greater reward for both of them than mutual betrayal.
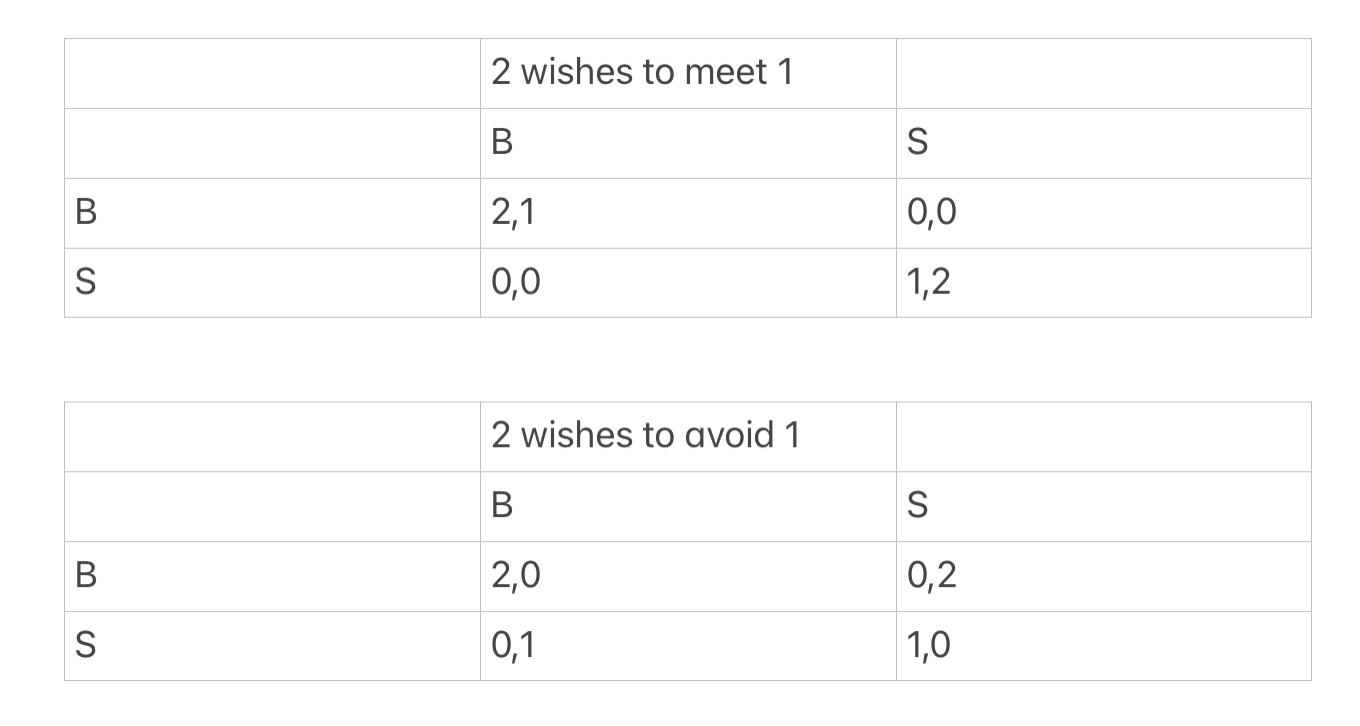
Battle of the sexes
The "battle of the sexes" is a term used to describe the perceived conflict between men and women in various areas of life, such as relationships, careers, and social roles. This conflict is often portrayed in popular culture, such as movies and television shows, as a humorous or dramatic competition between the genders. This conflict can be depicted in a game theory framework. This is an example of non-cooperative games.
An example of the "battle of the sexes" can be seen in the portrayal of relationships in popular media, where men and women are often depicted as being fundamentally different and in conflict with each other. For instance, in some romantic comedies, the male and female protagonists are shown as having opposing views on love and relationships, and they have to overcome these differences in order to be together.
In this game, there are two pure strategy Nash equilibria: one where both the players choose the same strategy and the other where the players choose different options. If the game is played in mixed strategies, where each player chooses their strategy randomly, then there is an infinite number of Nash equilibria. However, in the context of the "battle of the sexes" game, the assumption is usually made that the game is played in pure strategies.
Ultimatum game
The ultimatum game is a game that has become a popular instrument of
economic experiments. An early description is by Nobel laureate
John Harsanyi in 1961.
One player, the proposer, is endowed with a sum of money. The proposer is tasked with splitting it with another player, the responder (who knows what the total sum is). Once the proposer communicates his decision, the responder may accept it or reject it. If the responder accepts, the money is split per the proposal; if the responder rejects, both players receive nothing. Both players know in advance the consequences of the responder accepting or rejecting the offer. The game demonstrates how social acceptance, fairness, and generosity influence the players decisions.
Ultimatum game has a variant, that is the dictator game. They are mostly identical, except in dictator game the responder has no power to reject the proposer's offer.
Trust game
The Trust Game is an experiment designed to measure trust in economic decisions. It is also called "the investment game" and is designed to investigate trust and demonstrate its importance rather than "rationality" of self-interest. The game was designed by Berg Joyce, John Dickhaut and Kevin McCabe in 1995.
In the game, one player (the investor) is given a sum of money and must decide how much of it to give to another player (the trustee). The amount given is then tripled by the experimenter. The trustee then decides how much of the tripled amount to return to the investor. If the recipient is completely self interested, then he/she should return nothing. However that is not true as the experiment conduct. The outcome suggest that people are willing to place a trust, by risking some amount of money, in the belief that there would be reciprocity.
Cournot Competition
The Cournot competition model involves players choosing quantity of a homogenous product to produce independently and simultaneously, where
marginal cost can be different for each firm and the firm's payoff is profit. The production costs are public information and the firm aims to find their profit-maximizing quantity based on what they believe the other firm will produce and behave like monopolies. In this game firms want to produce at the monopoly quantity but there is a high incentive to deviate and produce more, which decreases the market-clearing price.
For example, firms may be tempted to deviate from the monopoly quantity if there is a low monopoly quantity and high price, with the aim of increasing production to maximize profit.
However this option does not provide the highest payoff, as a firm's ability to maximize profits depends on its market share and the elasticity of the market demand. The Cournot equilibrium is reached when each firm operates on their reaction function with no incentive to deviate, as they have the best response based on the other firms output.
Within the game, firms reach the Nash equilibrium when the Cournot equilibrium is achieved.

Bertrand Competition
The Bertrand competition assumes homogenous products and a constant marginal cost and players choose the prices.
The equilibrium of price competition is where the price is equal to marginal costs, assuming complete information about the competitors' costs. Therefore, the firms have an incentive to deviate from the equilibrium because a homogenous product with a lower price will gain all of the market share, known as a cost advantage.
In popular culture
* Based on
the 1998 book by
Sylvia Nasar, the life story of game theorist and mathematician
John Nash was turned into the 2001
biopic ''
A Beautiful Mind'', starring
Russell Crowe as Nash.
* The 1959
military science fiction
Military science fiction is a subgenre of science fiction and military fiction that depicts the use of science fiction technology, including spaceships and science fiction weapons, weapons, for military purposes and usually principal characters ...
novel ''
Starship Troopers'' by
Robert A. Heinlein mentioned "games theory" and "theory of games". In the 1997 film
of the same name, the character Carl Jenkins referred to his military intelligence assignment as being assigned to "games and theory".
* The 1964 film ''
Dr. Strangelove'' satirizes game theoretic ideas about
deterrence theory. For example, nuclear deterrence depends on the threat to retaliate catastrophically if a nuclear attack is detected. A game theorist might argue that such threats can fail to be ''credible'', in the sense that they can lead to subgame imperfect equilibria. The movie takes this idea one step further, with the Soviet Union irrevocably committing to a catastrophic nuclear response without making the threat public.
* The 1980s
power pop
Power pop (also typeset as powerpop) is a subgenre of rock music and form of pop rock based on the early music of bands such as the Who, the Beatles, the Beach Boys, and the Byrds. It typically incorporates melodic hooks, vocal harmonies, ...
band
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed ...
was founded by singer/songwriter
Scott Miller, who described the band's name as alluding to "the study of calculating the most appropriate action given an adversary... to give yourself the minimum amount of failure".
[.]
* ''
Liar Game'', a 2005 Japanese
manga
are comics or graphic novels originating from Japan. Most manga conform to a style developed in Japan in the late 19th century, and the form has a long history in earlier Japanese art. The term is used in Japan to refer to both comics ...
and 2007 television series, presents the main characters in each episode with a game or problem that is typically drawn from game theory, as demonstrated by the strategies applied by the characters.
* The 1974 novel ''
Spy Story'' by
Len Deighton explores elements of game theory in regard to cold war army exercises.
* The 2008 novel ''
The Dark Forest'' by
Liu Cixin explores the relationship between extraterrestrial life, humanity, and game theory.
* Joker, the prime antagonist in the 2008 film ''
The Dark Knight'' presents game theory concepts—notably the
prisoner's dilemma in a scene where he asks passengers in two different ferries to bomb the other one to save their own.
* In the 2018 film ''
Crazy Rich Asians'', the female lead Rachel Chu is a professor of economics and game theory at
New York University
New York University (NYU) is a private university, private research university in New York City, New York, United States. Chartered in 1831 by the New York State Legislature, NYU was founded in 1832 by Albert Gallatin as a Nondenominational ...
. At the beginning of the film she is seen in her NYU classroom playing a game of poker with her teaching assistant and wins the game by
bluffing; then in the
climax of the film, she plays a game of
mahjong with her boyfriend's disapproving mother Eleanor, losing the game to Eleanor on purpose but winning her approval as a result.
* In the 2017 film
Molly's Game, Brad, an inexperienced poker player, makes an irrational betting decision without realizing and causes his opponent Harlan to deviate from his Nash Equilibrium strategy, resulting in a significant loss when Harlan loses the hand.
See also
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Compositional game theory
Lists
*
List of cognitive biases
*
List of emerging technologies
This is a list of emerging technologies, which are emerging technologies, in-development technical innovations that have significant potential in their applications. The criteria for this list is that the technology must:
# Exist in some way; ...
*
List of games in game theory
Notes
References
Sources
*
*
*
*
*
*
*
*
* , (2002 edition)
*
* . A modern introduction at the graduate level.
*
*
*
*
*
*
* Consistent treatment of game types usually claimed by different applied fields, e.g.
Markov decision processes.
Further reading
Textbooks and general literature
* .
*
Description
* . Suitable for undergraduate and business students.
* . Suitable for upper-level undergraduates.
*
* . Suitable for advanced undergraduates.
** Published in Europe as .
*
* . Presents game theory in formal way suitable for graduate level.
* Joseph E. Harrington (2008) ''Games, strategies, and decision making'', Worth, . Textbook suitable for undergraduates in applied fields; numerous examples, fewer formalisms in concept presentation.
*
*
Michael Maschler;
Eilon Solan; Shmuel Zamir (2013), ''Game Theory'', Cambridge University Press, . Undergraduate textbook.
* . Suitable for a general audience.
*
* . A leading textbook at the advanced undergraduate level.
*
Historically important texts
*
*
*
*
*
:*reprinted edition:
*
*
*
Shapley, L.S. (1953), A Value for n-person Games, In: Contributions to the Theory of Games volume II, H. W. Kuhn and A. W. Tucker (eds.)
*
* English translation: "On the Theory of Games of Strategy," in A. W. Tucker and R. D. Luce, ed. (1959), ''Contributions to the Theory of Games'', v. 4, p
42.Princeton University Press.
*
*
Other material
*
Allan Gibbard, "Manipulation of voting schemes: a general result", ''Econometrica'', Vol. 41, No. 4 (1973), pp. 587–601.
* . A layman's introduction.
* .
*
*
*
*
*
*
External links
* James Miller (2015)
Introductory Game Theory Videos
*
* Paul Walker
* David Levine
Game Theory. Papers, Lecture Notes and much more stuff.* Alvin Roth: — Comprehensive list of links to game theory information on the Web
* Adam Kalai
Game Theory and Computer Science— Lecture notes on Game Theory and Computer Science
* Mike Shor
GameTheory.net— Lecture notes, interactive illustrations and other information.
* Jim Ratliff'
Graduate Course in Game Theory(lecture notes).
* Don Ross
Review Of Game Theoryin the ''Stanford Encyclopedia of Philosophy''.
* Bruno Verbeek and Christopher Morris
Game Theory and Ethics* Elmer G. Wiens
Game Theory— Introduction, worked examples, play online two-person zero-sum games.
* Marek M. Kaminski
— Syllabuses and lecture notes for game theory and political science.
* Kesten Green's — Se
Papersfo
evidence on the accuracy of forecasts from game theory and other methods.
* McKelvey, Richard D., McLennan, Andrew M., and Turocy, Theodore L. (2007)
Gambit: Software Tools for Game Theory'.
* Benjamin Polak
Open Course on Game Theory at Yalevideos of the course
* Benjamin Moritz, Bernhard Könsgen, Danny Bures, Ronni Wiersch, (2007)
Spieltheorie-Software.de: An application for Game Theory implemented in JAVA
'.
* Antonin Kucera
Stochastic Two-Player Games
* Yu-Chi Ho
What is Mathematical Game TheoryWhat is Mathematical Game Theory (#2)What is Mathematical Game Theory (#3)What is Mathematical Game Theory (#4)-Many person game theoryWhat is Mathematical Game Theory ?( #5) – Finale, summing up, and my own view
{{DEFAULTSORT:Game Theory
Artificial intelligence
Formal sciences
Mathematical economics
John von Neumann
 The work of
The work of  In 1950, John Nash developed a criterion for mutual consistency of players' strategies known as the
In 1950, John Nash developed a criterion for mutual consistency of players' strategies known as the  For example, where Player 1 is unsure whether Player 2 would rather date her or get away from her, while Player 2 understands Player 1's preferences as before. To be specific, supposing that Player 1 believes that Player 2 wants to date her under a probability of 1/2 and get away from her under a probability of 1/2 (this evaluation comes from Player 1's experience probably: she faces players who want to date her half of the time in such a case and players who want to avoid her half of the time). Due to the probability involved, the analysis of this situation requires to understand the player's preference for the draw, even though people are only interested in pure strategic equilibrium.
For example, where Player 1 is unsure whether Player 2 would rather date her or get away from her, while Player 2 understands Player 1's preferences as before. To be specific, supposing that Player 1 believes that Player 2 wants to date her under a probability of 1/2 and get away from her under a probability of 1/2 (this evaluation comes from Player 1's experience probably: she faces players who want to date her half of the time in such a case and players who want to avoid her half of the time). Due to the probability involved, the analysis of this situation requires to understand the player's preference for the draw, even though people are only interested in pure strategic equilibrium.
